(Doucet, 2010) の内容に基づき,証明を与えながら,条件付き Gauss 分布の特定と,効率的なシミュレーション法を議論し,線型Gauss 状態空間モデルのフィルタリング(特に Ensemble Kalman filter)に応用する.
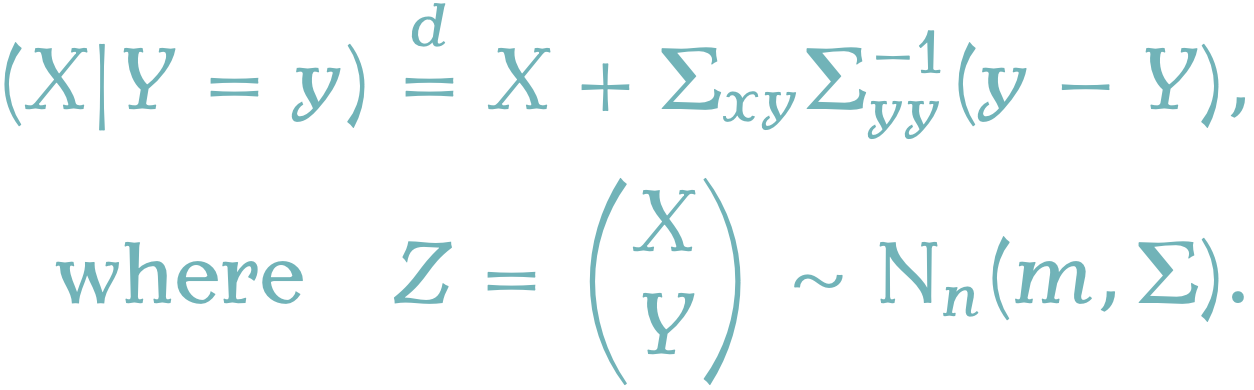
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1 正規確率変数同士の条件付き分布
\[Z=(X,Y)\sim\operatorname{N}_n(m,\Sigma)\] \[m=\begin{pmatrix}m_x\\m_y\end{pmatrix},\qquad\Sigma=\begin{pmatrix}\Sigma_{xx}&\Sigma_{xy}\\\Sigma_{xy}^\top&\Sigma_{yy}\end{pmatrix}\] で,共分散行列は正則 \(\Sigma\in\mathrm{GL}_n(\mathbb{R})\) とする.このとき, \[X|Y=y\sim\operatorname{N}_{n_x}(m_{x|y},\Sigma_{x|y}),\] \[m_{x|y}=m_x+\Sigma_{xy}\Sigma_{yy}^{-1}(y-m_y),\] \[\Sigma_{x|y}=\Sigma_{xx}-\Sigma_{xy}\Sigma_{yy}^{-1}\Sigma_{xy}^\top.\]
2 条件付き分布からのシミュレーション
条件付き確率変数 \(X|Y=y\) のシミュレーションは,条件付き共分散行列 \(\Sigma_{x|y}\) の Cholesky 分解 \(\Sigma_{x|y}=\sqrt{\Sigma_{x|y}}\left(\sqrt{\Sigma_{x|y}}\right)^\top\) を用いて, \[\overline{X}=m_{x|y}+\sqrt{\Sigma_{x|y}}U,\] \[U\sim\operatorname{N}_{n_x}(0,I_{n_x})\] によって行うのも直接的だが, \(n_x\) の次元が大きすぎる場合,Cholesky 分解の計算がネックとなる.そのような場合は, \[\overline{X}=X+\Sigma_{xy}\Sigma_{yy}^{-1}(y-Y),\] \[Z=\begin{pmatrix}X\\Y\end{pmatrix}\sim\operatorname{N}_n(m,\Sigma),\] というアルゴリズムを用いることが出来る (Hoffman and Ribak, 1991).
3 応用 Ensemble Kalman filter
また,Ensemble Kalman filter はこの手法の応用と理解することができ,この手法の別の応用として FFBS (Forward Filtering Backward Sampling) アルゴリズムを代替するサンプリングアルゴリズムを得ることが出来ることも論じている.
線型Gaussな状態空間モデル \[ \begin{cases} X_n=A_nX_{n-1}+a_n+W_n&n\ge 1,\\ Y_n=B_nX_n+b_n+V_n,&n\ge0. \end{cases} \] \[ W_n\sim\operatorname{N}_p(0,R^w_n),\quad V_n\sim\operatorname{N}_q(0,R_n^v), \]
の最適な一段階予測推定量 \[ \eta_n:=\mathcal{L}[X_n|(Y_0,\cdots,Y_{n-1})] \] も,フィルタリング推定量 \[ \widehat{\eta}_n:=\mathcal{L}[X_n|(Y_0,\cdots,Y_n)] \] も Gauss 確率変数で,平均と分散は 節 1 の命題の繰り返し適用によって計算できる.これを Kalman filter という.1
3.1 EnKF
しかし,状態空間(\(X_n\) の値域)の次元が大きすぎる場合,節 2 で述べた理由と同様の理由で,Kalman gain の行列計算が実行不可能になる.
このステップを,粒子平均によって代替する粒子法が Ensemble Kalman filter であり,前述の障碍が典型的に生じてきた地球科学・海洋科学の分野で発展してきた (Evensen, 1994).この方法では, 節 2 のサンプリングトリックを用いて,再帰的にフィルタリング分布と予測分布を近似していく.
3.2 FFBS
また,線型 Gauss 状態空間モデルのハイパーパラメータの推定が必要な場合などでは,Feynman-Kac 分布 \(p(x_{0:n}|y_{1:n})\) からのサンプリングが必要になる.
典型的には FFBS (Foward Filtering Backward Sampling) などの方法が知られている.これは \(p(x_{0:n}|y_{1:n})\) がある Markov 連鎖の見本道の分布に一致することに基づき,その後ろ向き核による分解から,
- 前向きにフィルタリング分布と予測分布を計算する再帰的アルゴリズムを実行する.
- 2つの分布から後ろ向き核を計算する.
- 後ろ向き核を用いて, \(X_n\sim p(x_n|y_{1:n})\) を後ろ向きにサンプリングしていく.
と実行する方法である.2
一方で, 節 2 のテクニックで次のようにしてサンプリングすることもできる.
- 前向きに \(\operatorname{E}[X_{0:n}|Y_{1:n}], \operatorname{E}[X_{0:n}|Y_{1:n}=y_{1:n}]\) を計算する.
- 次をサンプリングする: \[ \begin{align*} \overline{X}_{0:n}&:=\operatorname{E}[X_{0:n}|Y_{1:n}=y_{1:n}]\\ &\qquad+X_{0:n}-\operatorname{E}[X_{0:n}|Y_{1:n}] \end{align*} \]
(Durbin and Koopman, 2002) では,多くの場合 \(R^w_n\) のランクが低いことに注目して, \(\operatorname{E}[W_{1:n}|Y_{1:n}]\) を計算して, \(p(x_0,w_{1:n}|y_{1:n})\) からサンプリングすることを提唱している.
3.3 その他
(Doucet, 2010) は他にも,時空間統計 (Cressie, 1993) と機械学習 (Rasmussen and Williams, 2006) などで生じる Gauss 過程への応用で役に立ち得るのではないかと示唆している.
CardReferences
Footnotes
(Del Moral and Penev, 2014) p.280 など参照.↩︎
(Chopin and Papaspiliopoulos, 2020) 5.4.4節 p.63 など参照.↩︎