1 条件付き期待値の定義
条件付き期待値を,測度論から厳密に定義する際,ポイントは次の4点である.
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1.1 測度論による定義
\(\operatorname{E}[X|\mathcal{G}]\) は \(L^1(\Omega,\mathcal{G},\operatorname{P})\) の元であり,数学的対象としては「関数の同値類」である.関数としてはある零集合の上では定まらない.その任意の代表元も \(\operatorname{E}[X|\mathcal{G}]\) と表すことが多く,1 その場合は,多くの等式には a.s. (= almost surely) がついてまわることになる.
もちろん,\(L^1(\operatorname{P})\) 上の順序関係 \(\le\) を \[ X\le Y:\Leftrightarrow X\le Y\;\;\text{a.s.} \] と定義し,a.s. を省略して書いてもよい.
(Dudley, 2002, pp. 10.1節 p.336), (吉田朋広, 2006, p. 43) がおすすめな参照先.(舟木直久, 2004, p. 88) が入門しやすい.\(X\in L^2(\Omega)\) でいい場合は,より「射影」としてわかりやすい特徴付けがある( 節 1.3 ).これのおすすめは (Jacod and Protter, 2004, pp. 第23節 p.200), (Kallenberg, 2021, p. 164).
1.2 確率変数に関する条件付け
すると,\(X\) が \(\Omega\) 上に引き戻す \(\sigma\)-代数 \[ \sigma(X):=\left\{A\subset\Omega\mid\exists_{B\in\mathcal{E}}\; X^{-1}(B)=A\right\} \] を与えた下での条件付き期待値 \(\operatorname{E}[Y|\sigma(X)]\) と,次のように関係する.2 \(\operatorname{E}[Y|\sigma(X)]\) は定義 節 1.1 1から \(\sigma[X]\)-可測であるが,可測性の特徴付け(後述)から,これはあるBorel可測関数 \(f\) について,\[\operatorname{E}[Y|X]=f(X)\;\;\text{a.s.}\] と表せる.この \(f:\mathcal{X}\to\mathbb{R}\) が,\(X\) を与えた下での \(Y\) の条件付き期待値 \(\operatorname{E}[Y|X=-]\) である.
この記法 \(\operatorname{E}[Y|X=x]\) とは何かというと,\(X\) の値域 \(\mathcal{X}\) 上の関数として,新たに \[\operatorname{E}[Y|X=x]:=f(x)\;\;\text{a.s.}\] と書くことにするのである.3 すると, \[ \operatorname{E}[Y|X=x]|_{x=X(\omega)}=\operatorname{E}[Y|X](\omega)\;\;\text{a.s.} \] も満たす.つまり,次の図式が可換である:
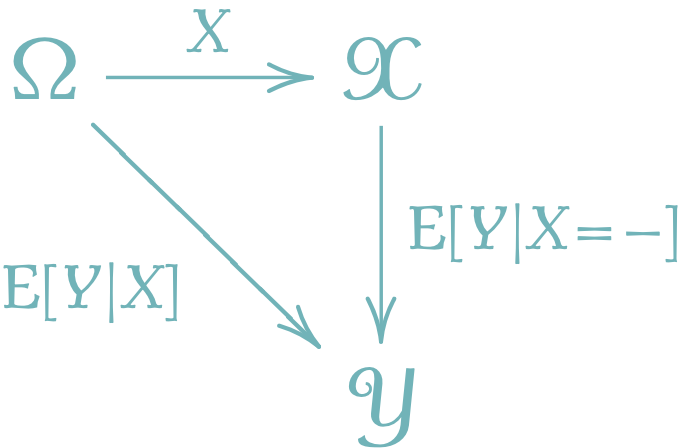
(Dudley, 2002, pp. 定理4.2.8 p.128) は \(S=\mathbb{R}\) の場合,(Landkov, 1972) は \(S=\mathbb{R}^m\) の場合, (Kallenberg, 2021, pp. 補題1.14 p.18) に一般の標準Borel空間の場合の証明がある.nLab も極めて参考になる.
1.3 射影としての特徴付け
\(L^2(\Omega)\subset L^1(\Omega)\) 上に議論を制限してみると,実は \(\mathcal{F}\) の部分 \(\sigma\)-代数 \(\mathcal{G}\) に関する条件付き期待値は,部分空間 \[ L^2_\mathcal{G}(\Omega):=\left\{X\in L^2(\Omega)\:\middle|\:X\,\text{は}\,\mathcal{G}\,\text{-可測}\right\} \] への射影になっている.
1.4 条件付き確率
しかしこの定義には問題がある.条件付き期待値 \(\operatorname{E}[X|\mathcal{G}]\) が \(\Omega\) 上 \(\operatorname{P}\text{-a.e.}\) でしか定まらない(場合がある)から,\(\operatorname{P}\) も一般には可算加法性をa.s.にしか満たさない: \[ \operatorname{P}\left[\bigcap_{n\in\mathbb{N}}A_n\,\middle|\,\mathcal{G}\right]=\sum_{n\in\mathbb{N}}\operatorname{P}[A_n]\;\;\text{a.s.} \] この式自体は後述の単調収束定理( 節 2.3 )から示せる.
だが,\(\mathcal{G}\) がある完備可分距離空間に値を取る確率変数 \(Y\) について \(\mathcal{G}=\sigma(Y)\) である場合など,殆どの場合で,うまく \(\operatorname{P}\) を取ることが出来る.5 このように,a.s. 抜きで正式に確率測度として定まる場合,その確率核 \(\operatorname{P}:E\times\mathcal{G}\to[0,1]\) を,正則条件付き確率と呼び分ける.
2 性質
2.1 作用素としての性質
\(\mathcal{G}\)-可測な可積分関数のなす部分空間を \(L_{\mathcal{G}}^1(\Omega)\subset L^1(\Omega)\) で表す.
2.2 Tower Property
2.3 単調収束定理
2.4 可測関数の取り出し
2.5 独立な場合
2.6 条件付き期待値のアトム上での値
条件付き確率の定義 節 1.4 から, \[ \operatorname{P}[Y\in B|X=x]:=\operatorname{E}[1_{\left\{Y\in B\right\}}|X=x] \] と議論できる.さらに \(\operatorname{P}[X=x]>0\) のとき, \[ \begin{align*} &=\frac{\operatorname{E}[1_{\left\{Y\in B\right\}}1_{\left\{X=x\right\}}]}{\operatorname{P}[X=x]}\\ &=\frac{\operatorname{P}[Y\in B,X=x]}{\operatorname{P}[X=x]} \end{align*} \] という見慣れた表示を得る.
3 更なる条件付け
3.1 条件付き独立性
\(\mathcal{C}=\boldsymbol{2}\) であるとき,通常の独立性に一致する(節 2.5 ).また全ての確率変数は \(\mathcal{F}\)-条件付き独立である(節 2.4 ).
3.2 条件付き分散
これは条件付き期待値が \(L^2(\Omega)\)-射影であるためである( 節 1.3 ).
確率変数 \(Y\in\mathcal{L}^2(\Omega)\) の \(\mathcal{G}\) に関する条件付き分散を \[ \begin{align*} \mathrm{V}[Y|\mathcal{G}]&:=\operatorname{E}\left[(Y-\operatorname{E}[Y|\mathcal{G}])^2|\mathcal{G}\right]\\ &=\operatorname{E}[Y^2|\mathcal{G}]-\operatorname{E}[Y|\mathcal{G}]^2 \end{align*} \] と定める.このとき,次の 全分散の公式 と呼ばれる関係が成り立つ: \[ \mathrm{V}[Y]=\operatorname{E}[\mathrm{V}[Y|\mathcal{G}]]+\mathrm{V}[\operatorname{E}[Y|\mathcal{G}]]. \]
3.3 条件付き共分散
証明は (Kallenberg, 2021) 補題8.2 p.166 など.
References
Footnotes
(Dudley, 2002, p. 340) など.↩︎
(Dudley, 2002, pp. 定理10.2.2 p.345).一般には Borel空間に値を取る確率変数について成り立つ (Kallenberg, 2021, p. 165).↩︎
(Kallenberg, 2021, pp. 170–171) 定理8.9 も参照.↩︎