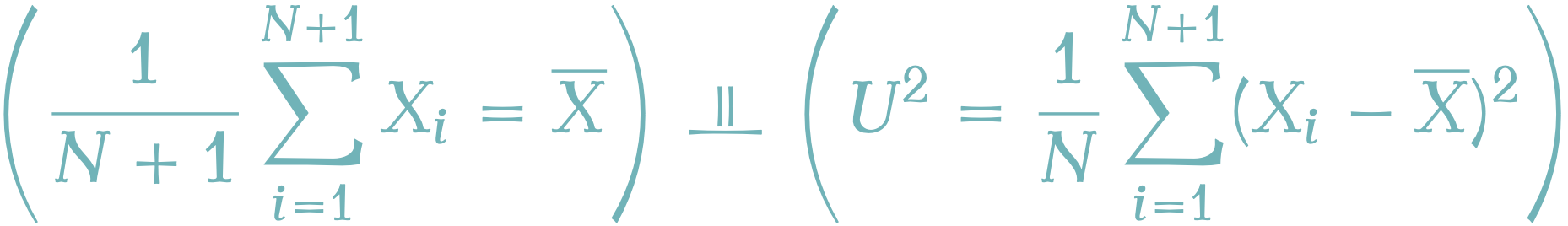次の命題の証明を与える.
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
正規標本 \(X_i\overset{\text{i.i.d.}}{\sim}\operatorname{N}_1(\mu,\sigma^2)\;(\mu\in\mathbb{R},\sigma^2>0)\) に対して,統計量を \[\overline{X}:=\frac{1}{N+1}\sum_{i=1}^{N+1}X_i,\] \[U^2:=\frac{1}{N}\sum_{i=1}^{N+1}(X_i-\overline{X})^2,\] と定める.このとき, \(\overline{X}\) と \(U^2\) とは独立である.
なお,この性質は正規分布を特徴付ける (Kawata and Sakamoto, 1949).
Helmert変換による証明
最も直接的で,示唆も深い. (竹村彰道, 2020) 第4.3節 pp.69-70 も参照.
次のように定まる行列 \(\mathbb{H}\in M_{N+1}(\mathbb{R})\) を Helmert行列 という. 最初の行を \[\mathbb{H}_{1,j}:=\frac{1}{\sqrt{N+1}},\qquad 1\le j\le N+1,\] とし,それ以下の行を \[\mathbb{H}_{i,j}:=\overline{\mathbb{H}}_{i,j}:=\begin{cases}
\frac{1}{\sqrt{i(i-1)}}&1\le j<i,\\
-\frac{i-1}{\sqrt{i(i-1)}}&j=i,\\
0&i<j\le N+1.
\end{cases}\] と定める.このとき, \[\mathbb{H}=\begin{pmatrix}\frac{\boldsymbol{1}_{N+1}^\top}{\sqrt{N+1}}\\\overline{\mathbb{H}}\end{pmatrix}\] と表せる.
Helmert行列 \(\mathbb{H}\in M_{N+1}(\mathbb{R})\) とその部分行列 \(\overline{\mathbb{H}}\in M_{N,N+1}(\mathbb{R})\) について,
- 直交行列である.
- 次を満たす:\[\overline{\mathbb{H}}^\top\overline{\mathbb{H}}=I-\frac{1}{N+1}J=\epsilon.\]
ただし,次のように定めた: \[
\epsilon:=I_{N+1}-\frac{J_{N+1}}{N+1},\qquad J_{N+1}:=\boldsymbol{1}_{N+1}\boldsymbol{1}_{N+1}^\top.
\]
- \(x,y\in\mathbb{R}^{N+1}\) に対して, \(x^\top\epsilon y=(x-\overline{x}\boldsymbol{1}_{N+1})^\top(y-\overline{y}\boldsymbol{1}_{N+1})\)
\(\mathbb{H}\) を具体的に書けば,
\[
\mathbb{H}:=\begin{pmatrix}\frac{1}{\sqrt{N+1}}&\frac{1}{\sqrt{N+1}}&\frac{1}{\sqrt{N+1}}&\frac{1}{\sqrt{N+1}}&\cdots&\cdots&\frac{1}{\sqrt{N+1}}\\
\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}&0&0&\cdots&\cdots&0\\
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{6}}&-\frac{2}{\sqrt{6}}&0&\cdots&\cdots&0\\
\vdots&\vdots&\vdots&\vdots&\ddots&\ddots&\vdots\\
\frac{1}{\sqrt{k(k-1)}}&\cdots&\frac{1}{\sqrt{k(k-1)}}&\frac{1-k}{\sqrt{k(k-1)}}&0&\cdots&0\\
\vdots&\ddots&\vdots&\vdots&\ddots&\ddots&\vdots\\
\frac{1}{\sqrt{N(N+1)}}&\cdots&\cdots&\cdots&\cdots&\frac{1}{\sqrt{N(N+1)}}&\frac{N}{\sqrt{N(N+1)}}
\end{pmatrix}
\]
- \(\mathbb{H}\) の任意の行は正規化されており,異なる行の間の内積は必ず零になることはすぐに判る.よって, \(\mathbb{H}\mathbb{H}^\top=I\).列についても同様であることが, \[
\frac{1}{N+1}+\sum_{k=1}^N\frac{1}{k(k+1)}=1
\] に注意すれば同様に判る.よって,
\[
\mathbb{H}\mathbb{H}^\top=I=\mathbb{H}^\top\mathbb{H}=\frac{1}{N+1}J+\overline{\mathbb{H}}^\top\overline{\mathbb{H}}.
\]
- 1.の最後の等式から従う.なお,1.の最後の等式は次のように判る:
\[
\left(\frac{\boldsymbol{1}_{N+1}}{\sqrt{N+1}}\;\overline{\mathbb{H}}^\top\right)\begin{pmatrix}\frac{\boldsymbol{1}_{N+1}^\top}{\sqrt{N+1}}\\\overline{\mathbb{H}}\end{pmatrix}=\frac{\boldsymbol{1}_{N+1}\boldsymbol{1}_{N+1}^\top}{N+1}+\overline{\mathbb{H}}^\top\overline{\mathbb{H}}.
\]
- \(\epsilon=I_{N+1}-\frac{\boldsymbol{1}_{N+1}\boldsymbol{1}_{N+1}^\top}{N+1}\) を具体的に書けば \[
\epsilon=\begin{pmatrix}
\frac{N}{N+1}&-\frac{1}{N+1}&-\frac{1}{N+1}&\cdots&-\frac{1}{N+1}\\
-\frac{1}{N+1}&\frac{N}{N+1}&-\frac{1}{N+1}&\cdots&-\frac{1}{N+1}\\
\vdots&\ddots&\ddots&\ddots&\vdots\\
-\frac{1}{N+1}&\cdots&\cdots&-\frac{1}{N+1}&\frac{N}{N+1}
\end{pmatrix}
\]
となるから, \[
\begin{align*}
x^\top\epsilon y&=\frac{1}{N+1}(x_1\;\cdots\;x_{N+1})\begin{pmatrix}(N+1)y_1-\sum_{i=1}^{N+1}y_i\\\vdots\\(N+1)y_{N+1}-\sum_{i=1}^{N+1}y_i\end{pmatrix}\\
&=\frac{1}{N+1}\left((N+1)\sum_{i=1}^{N+1}x_iy_i-\left(\sum_{i=1}^{N+1}x_i\right)\left(\sum_{i=1}^{N+1}y_i\right)\right)\\
&=\sum_{i=1}^{N+1}x_iy_i-(N+1)\overline{x}\cdot\overline{y}\\
&=\sum_{i=1}^{N+1}(x_iy_i-\overline{x}\overline{y})\\
&=\sum_{i=1}^{N+1}(x_i-\overline{x})(y_i-\overline{y})\\
&=(x-\boldsymbol{1}_{N+1}\overline{x})^\top(y-\boldsymbol{1}_{N+1}\overline{y}).
\end{align*}
\]
\(\mu=0,\sigma^2=1\) と仮定して示せば, 一般の \(X_i\) に対しても \(\frac{X_i-\mu}{\sigma}\sim\operatorname{N}(0,1)\) に対して同様の議論をすることで一般の場合の結果も得る.
\[X_{1:N+1}:=\begin{pmatrix}X_1\\\vdots\\X_{N+1}\end{pmatrix}\sim\operatorname{N}_{N+1}(0,I_{N+1})\]
に対して, \(Y_{1:N+1}:=\mathbb{H}X_{1:N+1}\) と定めると, \(\mathbb{H}\) は直交行列だからやはり \(Y\sim\operatorname{N}_{N+1}(0,I_{N+1})\).加えて,\(\mathbb{H}\) の構成から \[
Y_0=\frac{\boldsymbol{1}_{N+1}^\top}{\sqrt{N+1}}X_{1:N+1}=\sqrt{N+1}\cdot\overline{X}
\] が成り立っている.
補題の2.と3.から, \(Y_{2:N+1}=\overline{\mathbb{H}}X_{1:N+1}\) に注意して, \[
\begin{align*}
\|Y_{2:N+1}\|^2&=(\overline{\mathbb{H}}X_{1:N+1})^\top(\overline{\mathbb{H}}X_{1:N+1})\\
&=X_{1:N+1}^\top(\overline{\mathbb{H}}^\top\overline{\mathbb{H}})X_{1:N+1}\\
&=X_{1:N+1}^\top\epsilon X_{1:N+1}=\|X_{1:N+1}-\overline{X}\boldsymbol{1}_{N+1}\|^2\\
&=\sum_{i=1}^{N+1}(X_i^2-\overline{X}^2)\\
&=\sum_{i=1}^{N+1}(X_i-\overline{X})^2=NU^2.
\end{align*}
\]
以上より, \(\overline{X}\) は \(Y_1\) のみの関数で, \(S^2,U^2\) は \(Y_{2:N+1}\) のみの関数であるから,互いに独立である.
Basuの定理による証明
\(\{P_\theta\}_{\theta\in\Theta}\) を分布族, \((\mathcal{X},\mathcal{A}),(\mathcal{T},\mathcal{B}),(\mathrm{V},\mathcal{C})\) を可測空間とする. \(T:\mathcal{X}\to\mathcal{T}\) を \(\{P_\theta\}_{\theta\in\Theta}\) の完備十分統計量,統計量 \(V:\mathcal{X}\to\mathrm{V}\) の分布 \(P^V_\theta\) は \(\theta\) に依らないとする. このとき,任意の \(\theta\in\Theta\) に対して,\(T\) と \(V\) は独立である: \[P_\theta[T\in A,V\in B]=P_\theta[T\in A]P_\theta[V\in B]\qquad(A\in\mathcal{B},B\in\mathcal{C},\theta\in\Theta)\]
仮定より,\(p_B:=P_\theta[V\in B]\in\mathbb{R},q_B(T):=P_\theta[V\in B|T]:\mathcal{X}\to\mathbb{R}\) は \(\theta\in\Theta\) に依らない. これに対して,条件付き期待値の性質から \[p_B=E_\theta[1_B(V)]=E_\theta[E_\theta[1_B(V)|T]]=E_\theta[q_B(T)]\] であるから,\(E_\theta[p_B-q_B(T)]=0\) が従う. 完備性から,\(P_\theta[p_B=q_B(T)]=1\).よって,任意の \(\theta\in\Theta\) について, \[\begin{align*}
P_\theta[T\in A,V\in B]&=E_\theta[1_A(T)1_B(V)]\\
&=E_\theta[1_A(T)E_\theta[1_B(V)|T]]\\
&=E_\theta[1_A(T)q_B(T)]\\
&=E_\theta[1_A(T)p_B]\\
&=E_\theta[1_A(T)]p_B\\
&=P_\theta[T\in A]P_\theta[V\in B].
\end{align*}\]
これを用いて,次のように証明できる.
- 標本平均は平均の完備十分統計量である
- 標本分散は平均の補助統計量である
の2点を示せば,Basuの定理から,標本平均と標本分散は独立である:\(\overline{X}\perp\!\!\!\perp S^2\). 同様にして,標本平均と不偏分散も独立である.
- 分布族 \(\{\operatorname{N}(\mu,\sigma^2)^{\otimes n}\}_{\mu\in\mathbb{R}}\) は指数型であり, 統計量 \[T_1(x):=\sum_{i\in[n]}x_i=n\overline{X}\] は \(\mu\) の完備十分統計量である.
- 標本分散の分布は \[S^2:=\frac{1}{n}\sum_{i\in[n]}(X_i-\overline{X})^2\sim\chi^2(n-1)\] より,パラメータ\(\mu\in\mathbb{R}\)に依らない.
Fisher-Cochranの定理の考え方
総合研究大学院大学統計科学コース2021年8月実施の入試問題の第三問にて,本命題を背景とした問題が出題された.このアプローチは 節 1 の証明法を別の角度から見れる.
\[X_{1:n}=\begin{pmatrix}X_1\\\vdots\\X_n\end{pmatrix},\qquad X_i\overset{\text{i.i.d.}}{\sim}\operatorname{N}(\mu,\sigma^2),\] をGauss確率ベクトル,\(B\in M_{mn}(\mathbb{R}),A\in M_n(\mathbb{R})\) を対称行列とする.\(BA=O_{m,n}\) のとき,2つの確率変数 \(BX_{1:n}\) と \(X^\top_{1:n} AX_{1:n}\) とは独立になる.
\(A\) は対称行列だから,ある直交行列 \(U\in \mathrm{O}_n(\mathbb{R}),U^\top U=I_n\) を用いて,\(U^\top DU=A\) と対角化出来る.ただし, \(D:=\mathrm{diag}(a_1,\cdots,a_r)\in M_n(\mathbb{R}),r:=\operatorname{rank}A\) は対角行列とした. よって,\(Y_{1:n}:=UX_{1:n}\) と定めると,これは再び成分が互いに独立な正規確率変数のベクトル \(Y_{1:n}\sim\operatorname{N}_n(\mu U1_n,\sigma^2I_n)\) で, \[X_{1:n}^\top AX_{1:n}=(UX_{1:n})^\top D(UX_{1:n})=a_1Y_1^2+\cdots+a_rY_r^2,\] と表せる.
次に,\(BA=0\) より,\(\mathrm{Im}\,A\subset\mathrm{Ker}\;B\),従って双方の直交補空間を考えると \(\mathrm{Im}\,B\subset\mathrm{Ker}\;A\) でもあるから,\(BX_{1:n}\) は \(y_{r+1},\cdots,y_{n}\) のみによって表せる確率変数のベクトルである(使わないものも許す). よって,\(BX_{1:n}\) と \(X_{1:n}^\top AX_{1:n}\) は独立.
\(m=1,B:=\frac{1}{N+1}1_{N+1}^\top\) と \[A:=N\epsilon=\frac{N}{N+1}\begin{pmatrix}
N&-1&-1&\cdots&-1\\
-1&N&-1&\cdots&-1\\
\vdots&\ddots&\ddots&\ddots&\vdots\\
-1&\cdots&\cdots&-1&N
\end{pmatrix}\in M_{N+1}(\mathbb{R})\] と定めると,\(BA=O\) であり,同時に \(\overline{X}=BX_{1:N+1}\) かつ \(U^2=X^\top_{1:N} AX_{1:N}\) である.
References
Basu, D. (1955). On statistics independent of a complete sufficient statistic. Sankhyā: The Indian Journal of Statistics, 15(4), 377–380.
Del Moral, P., and Horton, E. (2023). A theoretical analysis of one-dimensional discrete generation ensemble kalman particle filters. The Annals of Applied Probability, 33(2), 1327–1372.
Kawata, T., and Sakamoto, H. (1949). On the characterisation of the normal population by the independence of the sample mean and the sample variance. Journal of Mathematical Society of Japan, 1(2), 111–115.
竹村彰道. (2020). 現代数理統計学. 学術図書.