Hirofumi Shiba - YUIMA 入門

概要

R パッケージyuimaは，従来の i.i.d. 仮定の下での統計推測から，一般の確率過程の統計推測への橋渡しをすべく，広範な確率微分方程式のシミュレーションと統計推測を可能とするパッケージです．その機能の全貌と，基本的な使い方を紹介します．

1 YUIMAとは？

R パッケージyuimaは，Lévy 過程または分数 Brown 運動が駆動する確率微分方程式が定める過程という，極めて一般的なクラスの確率過程を扱う基盤パッケージである．

加えて，シミュレーションと推論のためのメソッドが提供されている．

R で通常の統計推測に用いられるformulaオブジェクトのように，直感的な記法でモデル（yuima.modelオブジェクト）を定義できる．

yuima.modelオブジェクトに対してtoLatex()関数を適用すると，モデルを LaTeX 記法で記述した文字列に変換することもできる．¹

このように YUIMA は，確率微分方程式の更なる研究や，より複雑なモデルや推測手続きのための基盤インフラとなることを目指している．²

リンク集

R-Forge ³
Stable version on CRAN.
GitHub
yuimaGUI package
rdrr.io ページ ⁴
論文 (Brouste et al., 2014)
- パッケージ開発者らによるオープンアクセス論文．

インストール

install.packages("yuima", repos="http://R-Forge.R-project.org")

library(yuima)  # ライブラリの読み込み

??yuima  # Man pageを開く

2 YUIMAの構造とモデル定義

2.1 クラス構造

各クラスの含まれる属性・スロット（上段）と，そのクラスのオブジェクトに使えるメソッド（下段），そして継承関係は以下の通りである．yuimaクラスは，複数の構成要素（モデル，データ，手法）の集約になっている．⁵

classDiagram
  yuima o-- yuima_model
  yuima o-- yuima_sampling
  yuima o-- yuima_data
  yuima_model o-- model_parameter
  class yuima{
    yuima.model::model
    yuima.sampling::sampling
    yuima.data::data
    -yuima.characteristic::characteristic 
    -yuima.functional::functional
    initialize()
    show()
    plot()
    simulate()
  }
  class yuima_model{
    expr::drift
    expr::diffusion
    num::hurst
    chr::time.variable
    chr::state.variable
    chr::solve.variable
    -model.parameter::parameter
    simulate()
  }
  class yuima_sampling{
    num::Initial
    num::Terminal
    num::n
    -num::delta
    -list[num]::grid
  }
  class yuima_data{
    original.data
    zoo.data
  }
  class model_parameter{
    list[chr]::all
    chr::common
    chr::diffusion
    chr::drift
    chr::jump
    chr::measure
  }

classDiagram
  yuima o-- yuima_characteristic
  yuima o-- yuima_functional
  class yuima{
    yuima.model::model
    yuima.sampling::sampling
    yuima.data::data
    yuima.characteristic::characteristic 
    yuima.functional::functional
    initialize()
    show()
    simulate()
  }
  class yuima_characteristic{
    int::equation.number
    num::time.scale
  }
  class yuima_functional{
    F
    list::f
    num::xinit
    num::e
  }

2.2 `setModel()`コンストラクタ

yuima.model.Rにおいて次の定義を持つ，yuima.modelオブジェクトのコンストラクタである．

setModel <- function(drift=NULL,
                     diffusion=NULL,
                     hurst=0.5,
                     jump.coeff=NULL,
                     measure=list(),
                     measure.type=character(),
                     state.variable="x",
                     jump.variable="z",
                     time.variable="t",
                     solve.variable,
                     xinit=NULL){...}

2.3 1次元の場合

拡散モデル（Ornstein-Uhlenbeck過程） \[ dX_t=\theta(\mu-X_t)\,dt+\sigma\,dW_t,\quad (\mu,\theta,\sigma,X_0)=(0,1,0.5,0) \] からシミュレーションをするためのサンプルコードは次の通り．他に，駆動過程を一般のHurst指数 $H$ についての分数Brown運動 $W^H$ としたり，ジャンプを導入したモデルを指定することもできる．⁶

Code

# 確率微分方程式モデルの設定
model <- setModel(drift = "theta*(mu-X)", diffusion = "sigma", state.variable = "X")

# サンプリングスキームの設定
sampling <- setSampling(Initial = 0, Terminal = 3, n = 1000)

# yuimaオブジェクトの作成
yuima <- setYuima(model = model, sampling = sampling)

# シミュレーションの実行
simulation <- simulate(yuima, true.parameter = c(mu = 0,theta = 1, sigma = 0.5), 
                       xinit = 0.02)

Code

# 結果のプロット
plot(simulation)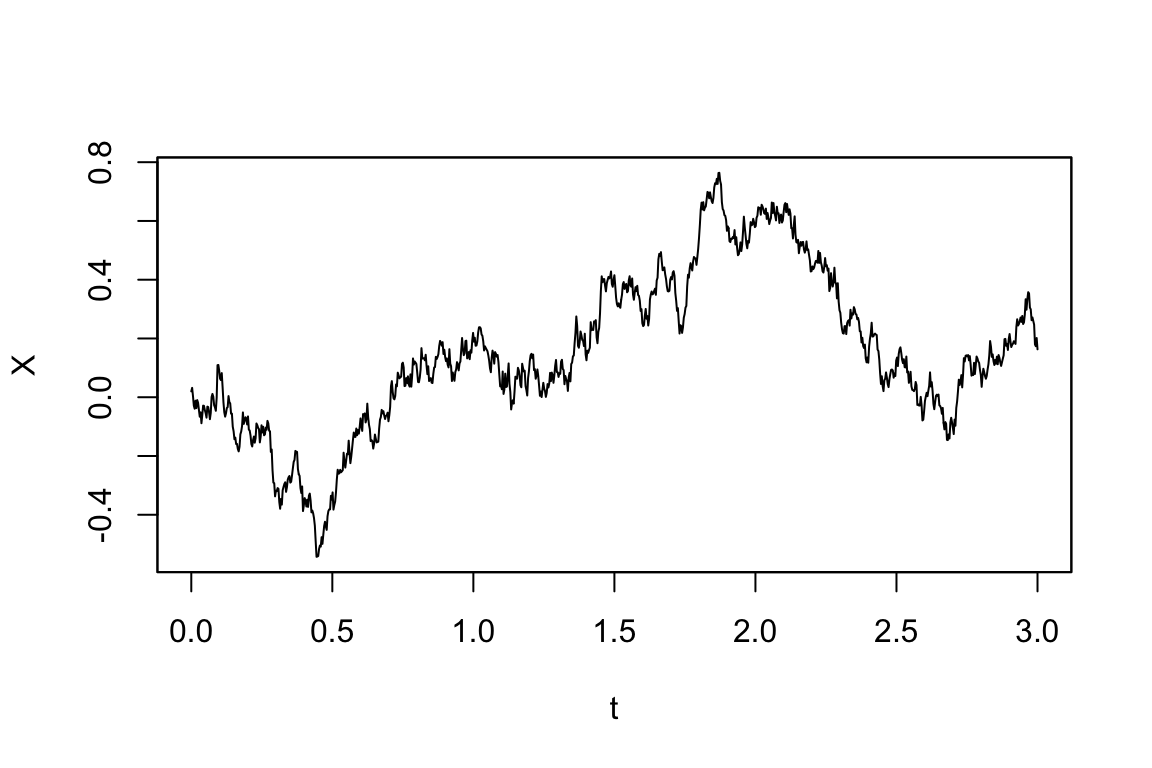

2.4 多次元の場合

まず，所望のモデルを行列の言葉で書く．例えば，2次元の場合で次のようなモデルを考える： \[ \begin{pmatrix}dX_t^{(1)}\\dX_t^{(2)}\end{pmatrix}=\begin{pmatrix}-3X_t^{(1)}\\-X_t^{(1)}2X_t^{(2)}\end{pmatrix}dt+\begin{pmatrix}1&0&X_t^{(2)}\\X_t^{(1)}&3&0\end{pmatrix}\begin{pmatrix}dW_t^{(1)}\\dW_t^{(2)}\\dW_t^{(3)}\end{pmatrix} \]

シミュレーションは次のように，各項の係数をベクトル・行列の形式でsetModelへと引き渡すことで行える．この場合，左辺を明示するためにsolve.variableのベクトルとしての指定が欠かせなくなる．⁷

Code

solve_variable <- c("X1", "X2")
drift <- c("-3*X1", "-X1-2*X2")
diffusion <- matrix(c("1", "X1", "0", "3", "X2", "0"), 2, 3)
model <- setModel(drift=drift, diffusion=diffusion, solve.variable=solve_variable)
simulation <- simulate(model)

Code

plot(simulation, plot.type="single", lty=1:2)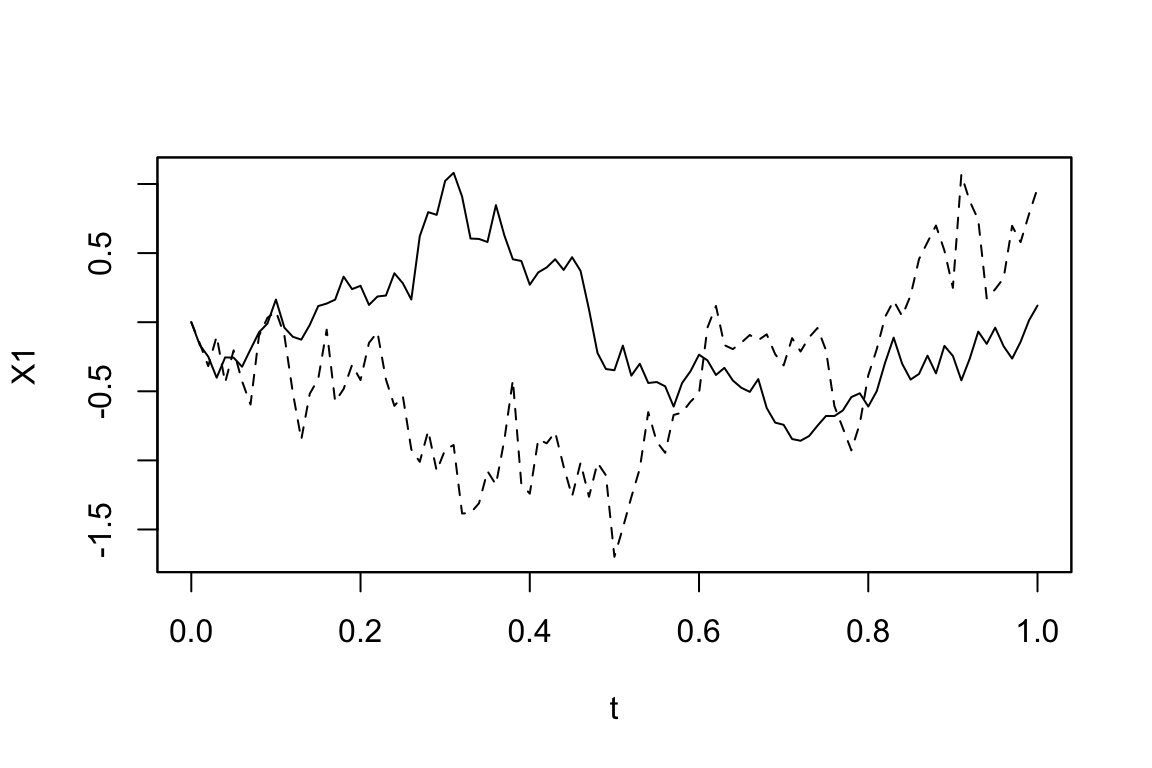

2.5 分数Gaussなノイズ

標準分数Brown運動 $W^H$ とは，Hurst指数 $H\in(0,1)$ に対して， \[ \operatorname{E}[W^H_s,W^H_t]=\frac{1}{2}\biggr(\lvert s\rvert^{2H}+\lvert t\rvert^{2H}-\lvert t-s\rvert^{2H}\biggl) \] という共分散構造を持った中心Gauss過程である．$H\ne1/2$ のとき，もはやMarkov過程でもセミマルチンゲールでもない．特に $H>1/2$ のときに長期的な依存を持った振る舞いをし，これが多くの応用を呼んでいる．これに対して，SDE \[ dX_t=a(X_t)dt+b(X_t)dW_t^H \] で定まるモデルを定義できる．(Brouste et al., 2014, pp. 3.5節 p.15)

例えば，次の分数OU過程 \[ dY_t=3Y_tdt+dW_t^H \] は次のように定義する：

Code

mod4A <- setModel(drift="3*y", diffusion=1, hurst=0.3, solve.var="y")
mod4B <- setModel(drift="3*y", diffusion=1, hurst=0.7, solve.var="y")
sim1 <- simulate(mod4A, sampling = setSampling(n=1000))
sim2 <- simulate(mod4B, sampling = setSampling(n=1000))
par(mfrow=c(2,1), mar=c(2,3,1,1))

Code

plot(sim1, main="H=0.3")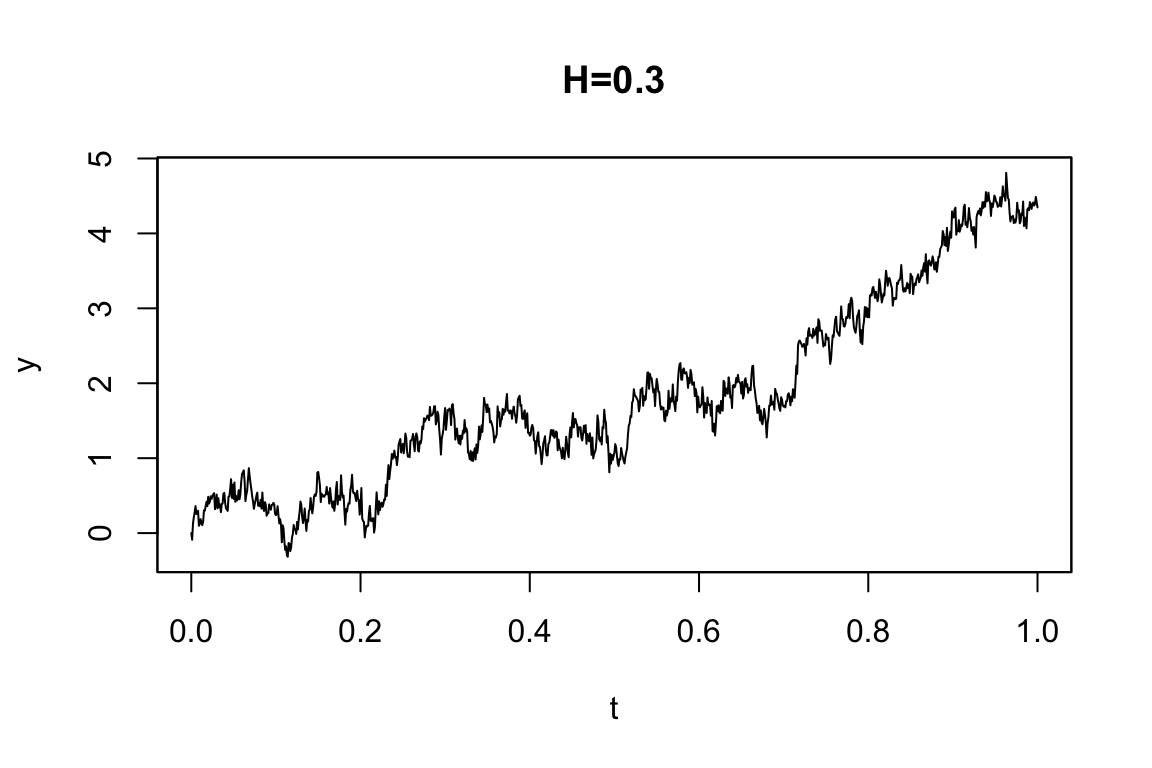

Code

plot(sim2, main="H=0.7")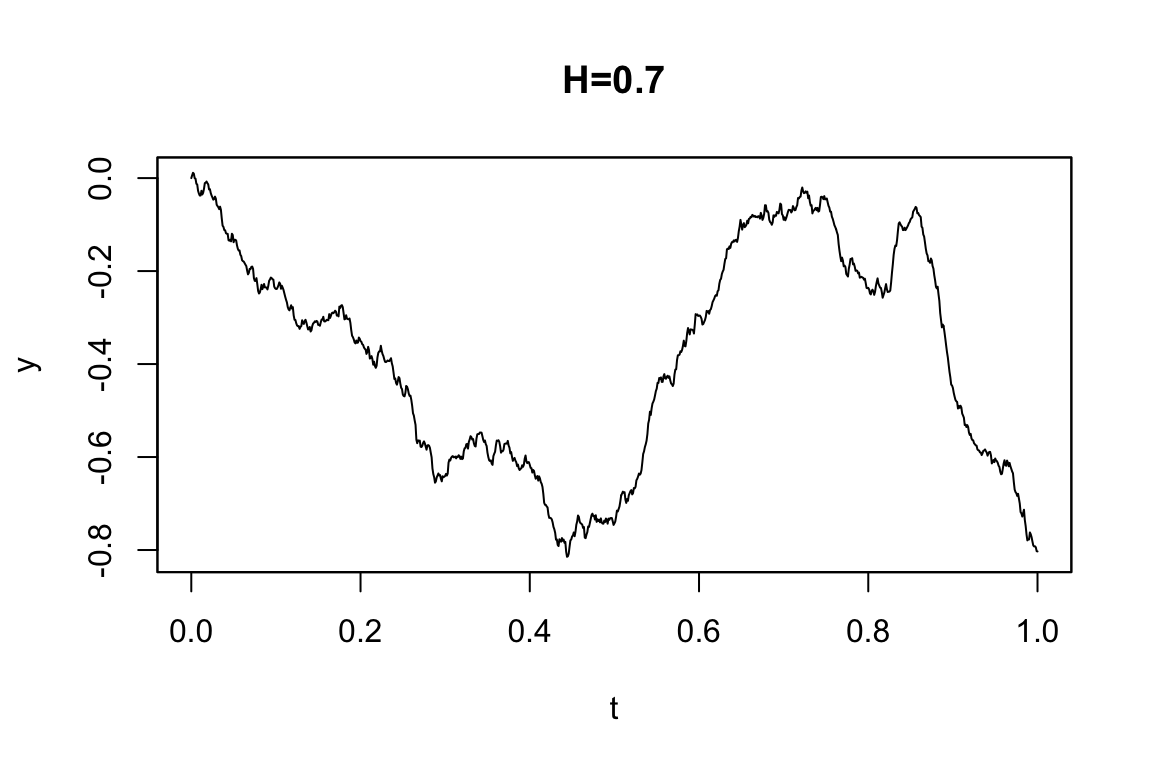

このシミュレーション法はCholesky法と(Wood and Chan, 1994) 法から選択が可能である．simulateメソッドのキーワード引数methodfGn="WoodChan", methodfGn="Cholesky"によって可能である．

2.6 Lévy過程

複合Poisson過程 $Z_t$ とは，Poisson時間に特定の分布に従うサイズの跳躍が起こるという過程である．これを用いて， \[ dX_t=a(t,X_t,\theta)dt+b(t,X_t,\theta)dW_t+dZ_t \] というSDEを通じてジャンプを持つ過程が定義できる．さらに $Z_t$ の項に係数 $c$ を持たせるには，$X$ のジャンプを定めるランダム測度 \[ \mu(dt,dz)=\sum_{s>0}1_{\left\{\Delta Z_s\ne 0\right\}}\delta_{(s,\Delta Z_s)}(dt,dz) \] により，複合Poisson過程が \[ Z_t=\int^t_0\int_{\lvert z\rvert\le1}z(\mu(ds,dz)-\nu(dz)ds)+\int^t_0\int_{\lvert z\rvert>1}z\mu(ds,dz) \] と表せ，ジャンプ過程 $X$ が，一般の関数 $c$ を用いて \[ dX_t=a(t,X_t,\theta)dt+b(t,X_t,\theta)dW_t+\int_{\lvert z\rvert>1}c(X_{t-},z)\mu(dt,dz) \] \[ \qquad+\int_{0<\lvert z\rvert\le1}c(X_{t-},z)(\mu(dt,dz)-\nu(dz)dt) \] と表せる．

$\nu\in\mathcal{P}(\mathbb{R}^d)$ がLévy測度であるとは， $\nu(\{0\})=0$ かつ \[ \int_{\mathbb{R}^d}(1\land\lvert z\rvert^2)\nu(dz)<\infty \] を満たすことをいう．

例えば，強度 $\lambda=10$ でGauss分布で大きさが決まる跳躍を持つLévy過程は，measure.type="CP"によって指定する．平均 $0$ のOU過程 \[ dX_t=-\theta X_tdt+\sigma dW_t+dZ_t \] は次のように定義できる：

Code

mod5 <- setModel(drift=c("-theta*x"), diffusion="sigma", jump.coeff="1",
      measure=list(intensity="10", df=list("dnorm(z,0,1)")), measure.type="CP",
      solve.variable="x")
sim5 <- simulate(mod5, true.p = list(theta=1, sigma=3), sampling=setSampling(n=1000))

Code

plot(sim5)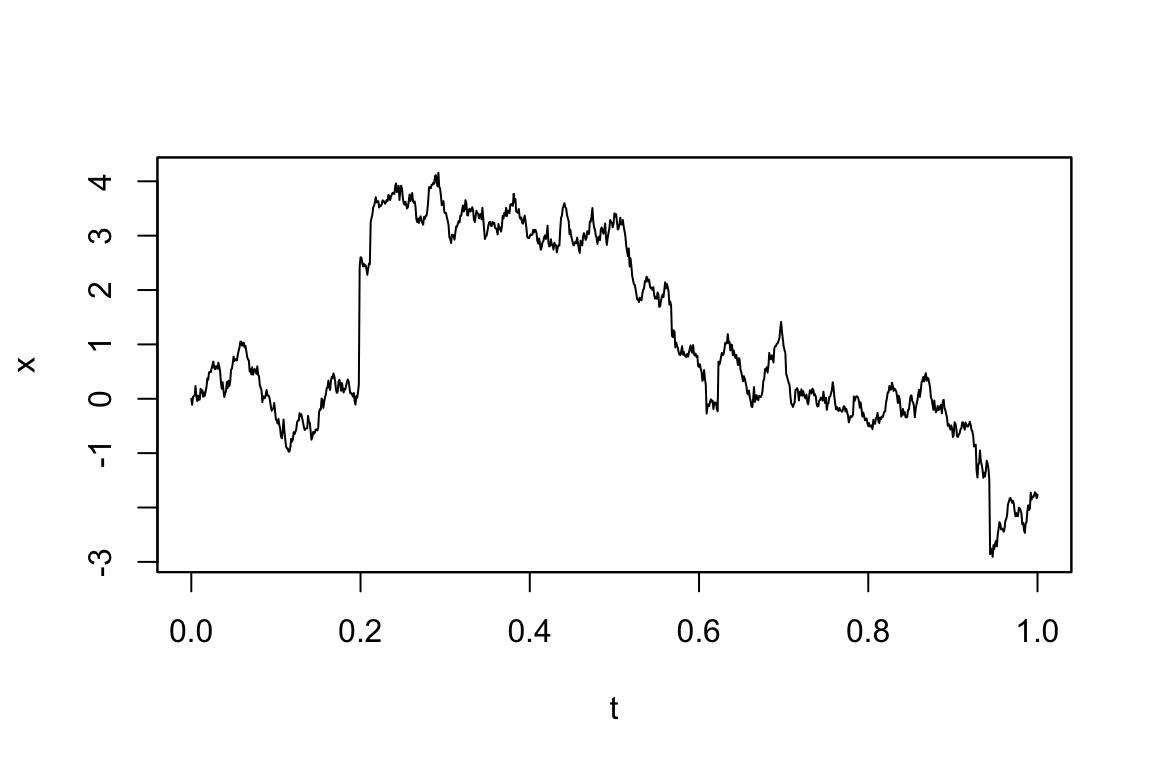

一方で，逆正規分布の大きさのジャンプを持つLévy測度 $\nu$ をもち，Poisson成分を持たないOU過程 \[ dX_t=-xdt+dZ_t \] は次のように定義できる：

Code

mod6 <- setModel(drift="-x", xinit=1, jump.coeff="1",
      measure.type="code", measure=list(df="rIG(z,1,0.1)"))
sim6 <- simulate(mod6, sampling=setSampling(Terminal=10, n=10000))

Code

plot(sim6)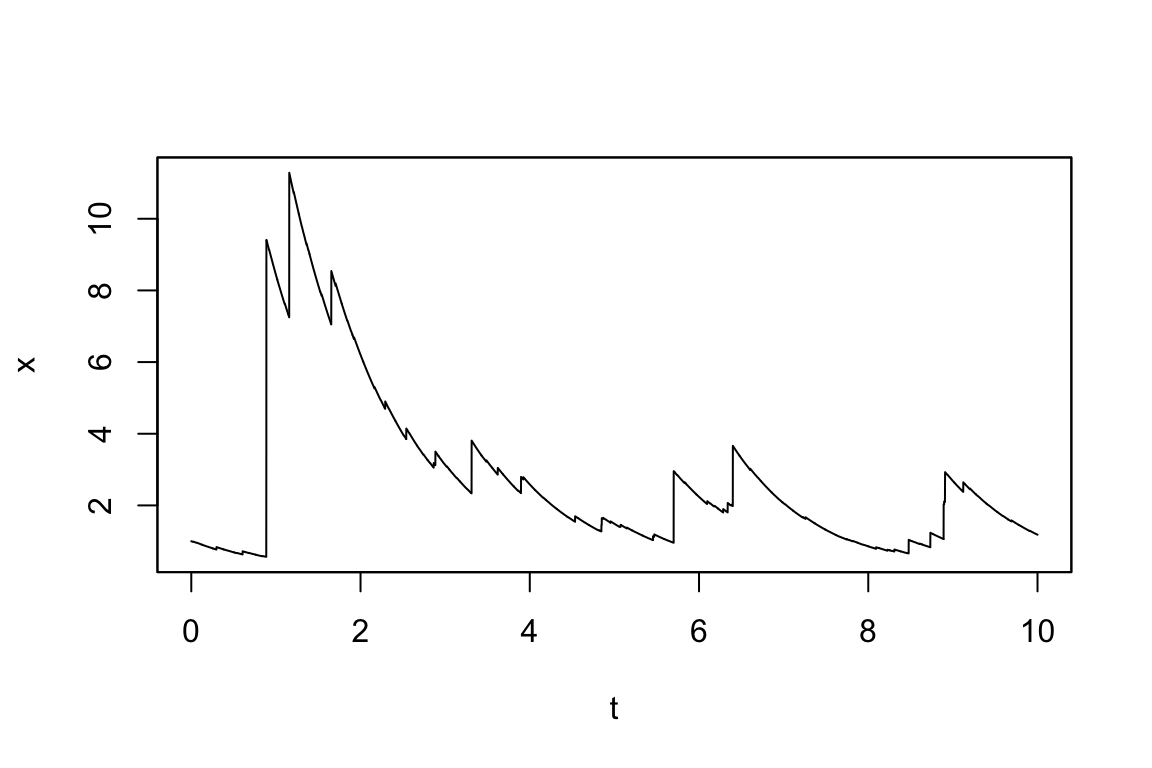

3 シミュレーションとサンプリング

3.1 `simulate()`関数の使い方

yuimaまたはyuima.modelで定められたモデルから，Euler-Maruyama法によるシミュレーションを実行する関数．⁸ simulate.Rにてポリモーフィックな実装がなされている．

simulate(object, nsim=1, seed=NULL, xinit, true.parameter, space.discretized = FALSE, 
 increment.W = NULL, increment.L = NULL, method = "euler", hurst, methodfGn = "WoodChan",
    sampling=sampling, subsampling=subsampling, ...)

返り値は，引数objectに，シミュレーション結果をyuima.dataフィールドに格納したyuimaオブジェクトであり，それに対してplot()が使える．

objectがyuimaオブジェクトの場合

3.2 時間離散化Euler-Maruyama法

時間にグリッド $0=\tau_0<\tau_1<\cdots<\tau_j<\cdots$ を導入し，連続過程 $\{X_t\}_{t\in\mathbb{R}_+}$ の離散化 $\{\widetilde{X}_{\tau_j}\}_{j\in\mathbb{N}}$ を \[ \widetilde{X}_{\tau_{j+1}}:=\widetilde{X}_{\tau_j}+b(\tau_j,\widetilde{X}_{\tau_j})(\tau_{j+1}-\tau_j)+c(\tau_j,\widetilde{X}_{\tau_j})(W_{\tau_{j+1}}-W_{\tau_j}) \]

と定義する． $W_{\tau_{j+1}}-W_{\tau_j}\overset{\text{iid}}{\sim}\mathrm{N}(0,\tau_{j+1}-\tau_j)$ を利用してサンプリングできる．

3.3 空間離散Euler-Maruyama法

simulateメソッドはこの方法も（ジャンプを持たない過程について）実装している．現状，駆動過程が1次元のSDEに対してのみである．

これは，時間離散化 $\{\tau_j\}_{j\in\mathbb{N}}\subset\mathbb{R}$ は次のように取る方法である： \[ \tau_0:=0,\quad\tau_{j+1}:=\inf\left\{t>\tau_j\mid\lvert W_t-W_{\tau_j}\rvert=\epsilon\right\} \] ただし，実装の上では \[ \epsilon^2:=\frac{T}{n}=\Delta_n \] としている．この方法は通常の時間離散化法よりも3倍高速になることが経験的に知られている．これはspace.discretized=TRUEで指定できる．デフォルトは=FALSEとなっており，時間離散化の方である．

他にも (Iacus, 2008) のシミュレーション法が実装予定である．

3.4 `setSampling`コンストラクタ

simulate関数はyuima.samplingオブジェクトも引数としてsampling = sampというように受け入れる．そして出力にそのまま引き継がれる．

setSampling.Rd

setSampling(Initial = 0, Terminal = 1, n = 100, delta, 
   grid, random = FALSE, sdelta=as.numeric(NULL), 
   sgrid=as.numeric(NULL), interpolation="pt" )

例えば次の2次元モデルを考える

\[ dX_t^{(1)}=-\theta X^{(1)}_tdt+dW_t^{(1)}+X_t^{(2)}dW_t^{(3)} \] \[ dX_t^{(2)}=-(X_t^{(1)}+\gamma X_t^{(2)})dt+X_t^{(1)}dW_t^{(1)}+\delta dW_t^{(2)} \]

時区間 $[0,3]$ 上のグリッドから $n=3000$ の粒度で観測するサンプリングオブジェクトは次のように定義する：

Code

sol <- c("x1", "x2")
b <- c("-theta*x1", "-x1-gamma*x2")
s <- matrix(c("1", "x1", "0", "delta", "x2", "0"), 2, 3)
myModel <- setModel(drift=b, diffusion=s, solve.variable=sol)
samp <- setSampling(Terminal=3, n=3000)

Code

sim2 <- simulate(myModel, sampling=samp)
str(sim2@sampling)

Formal class 'yuima.sampling' [package "yuima"] with 11 slots
  ..@ Initial      : num 0
  ..@ Terminal     : num [1:2] 3 3
  ..@ n            : int [1:2] 3000 3000
  ..@ delta        : num 0.001
  ..@ grid         :List of 1
  .. ..$ : num [1:3001] 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 ...
  ..@ random       : logi FALSE
  ..@ regular      : logi TRUE
  ..@ sdelta       : num(0) 
  ..@ sgrid        : num(0) 
  ..@ oindex       : num(0) 
  ..@ interpolation: chr "pt"

これはsampそのものである．

3.5 `subsampling`関数の使い方

２つの独立な指数分布を指定することで，Poisson到着時間を用いてサンプリングする，というyuima.samplingオブジェクトは次のように定義する：

Code

newsamp <- setSampling(random=list(rdist=c(function(x)
      + rexp(x, rate=10), function(x) rexp(x, rate=20))))

これを用いてサブサンプリングを実行できる：

Code

newdata <- subsampling(sim2, sampling=newsamp)
plot(sim2, plot.type="single", lty=c(1,3), ylab="sim2")
points(get.zoo.data(newdata)[[1]], col="red")
points(get.zoo.data(newdata)[[2]], col="green", pch=18)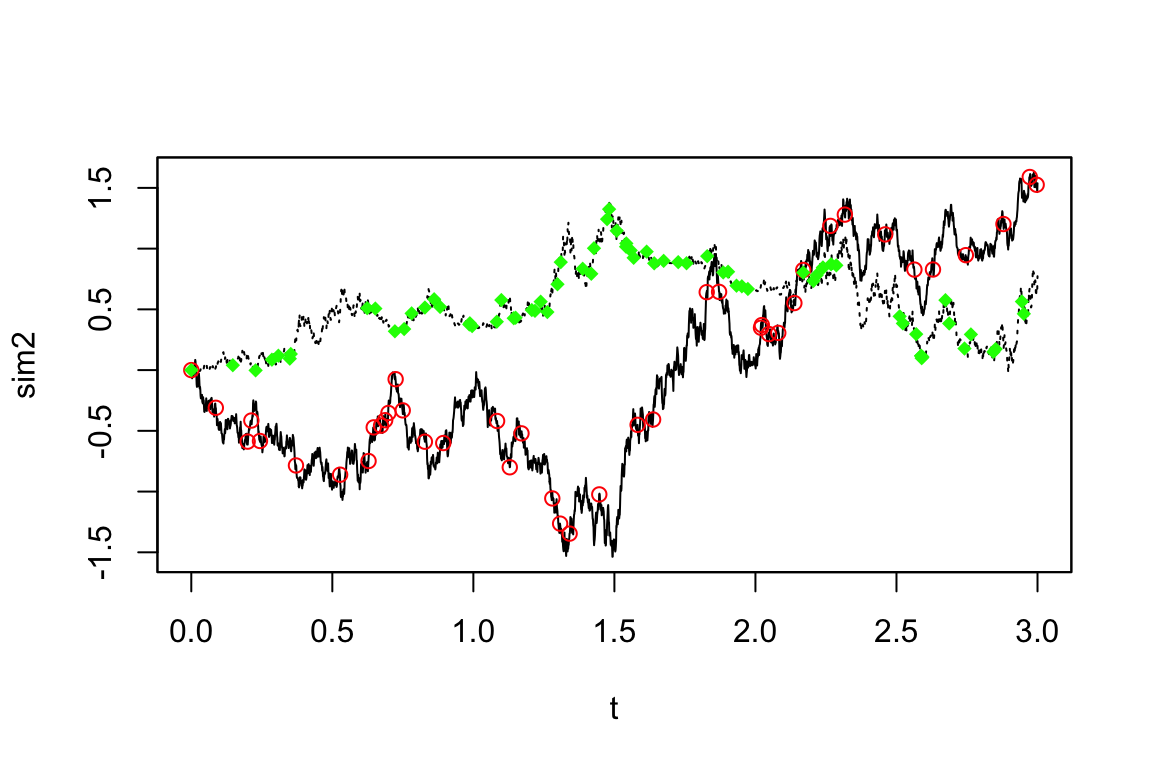

赤が $X_t^{(1)}$，緑が $X_t^{(2)}$ の見本道でどこがサブサンプリングされたかを示している．

このサンプリング法はランダムに行った．これを示すフラグがregularである：

Code

str(newsamp@regular)

 logi FALSE

一方で，決定論的に，決まった周波数でサブサンプリングもできる：

Code

newsamp2 <- setSampling(delta=c(0.1, 0.2))

Warning in yuima.warn("'Terminal' (re)defined."): 
YUIMA: 'Terminal' (re)defined.

Code

newdata2 <- subsampling(sim2, sampling=newsamp2)
plot(sim2, plot.type="single", lty=c(1,3), ylab="sim2")
points(get.zoo.data(newdata2)[[1]], col="red")
points(get.zoo.data(newdata2)[[2]], col="green", pch=18)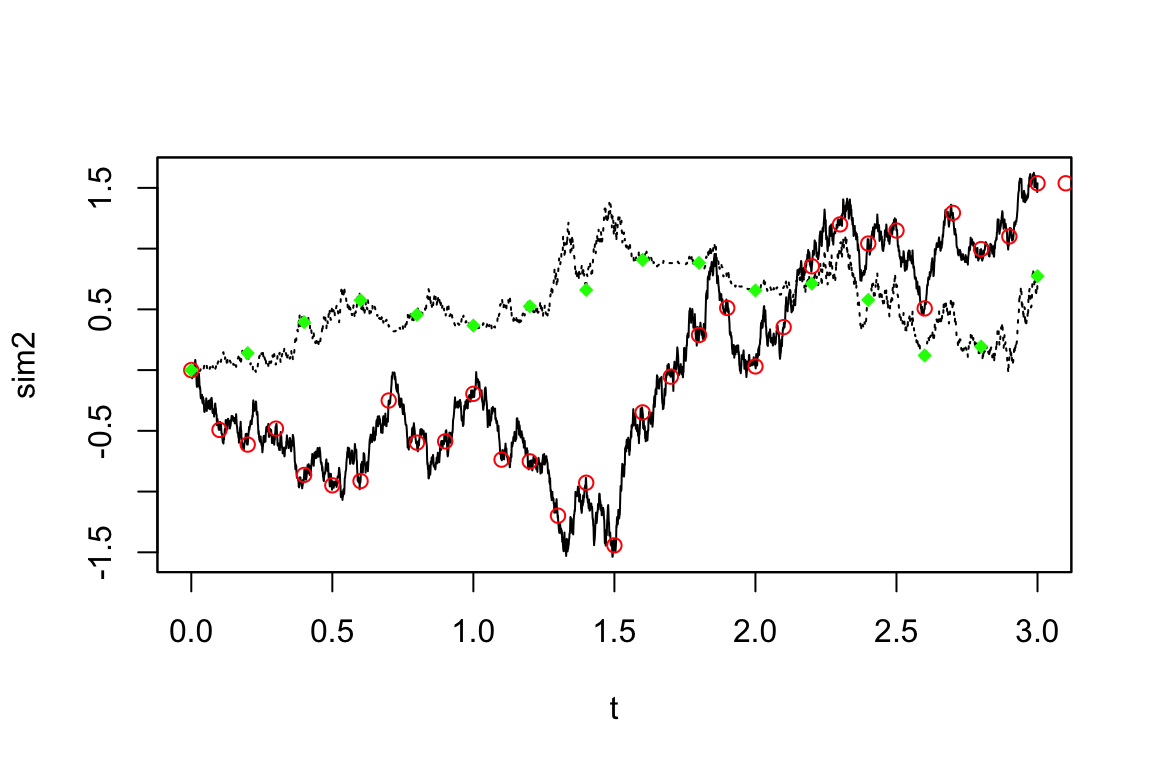

赤色のサブサンプリングは，緑色の２倍の頻度（半分の周波数）で行われている．

3.6 サンプリングとサブサンプリングの組み合わせ

シミュレーション研究で，よく高頻度のサンプリングを行った後，推定のためにより低い頻度でのデータを抽出する，ということが行われる．これは１行で表現できる：

Code

Y.sub <- simulate(myModel, sampling=setSampling(delta=0.001, n=1000), subsampling=setSampling(delta=0.01, n=100))
Y <- simulate(myModel, sampling=setSampling(delta=0.001, n=1000))

Code

plot(Y.sub, plot.type="single")
points(get.zoo.data(Y.sub)[[1]], col="red")
points(get.zoo.data(Y.sub)[[2]], col="green", pch=18)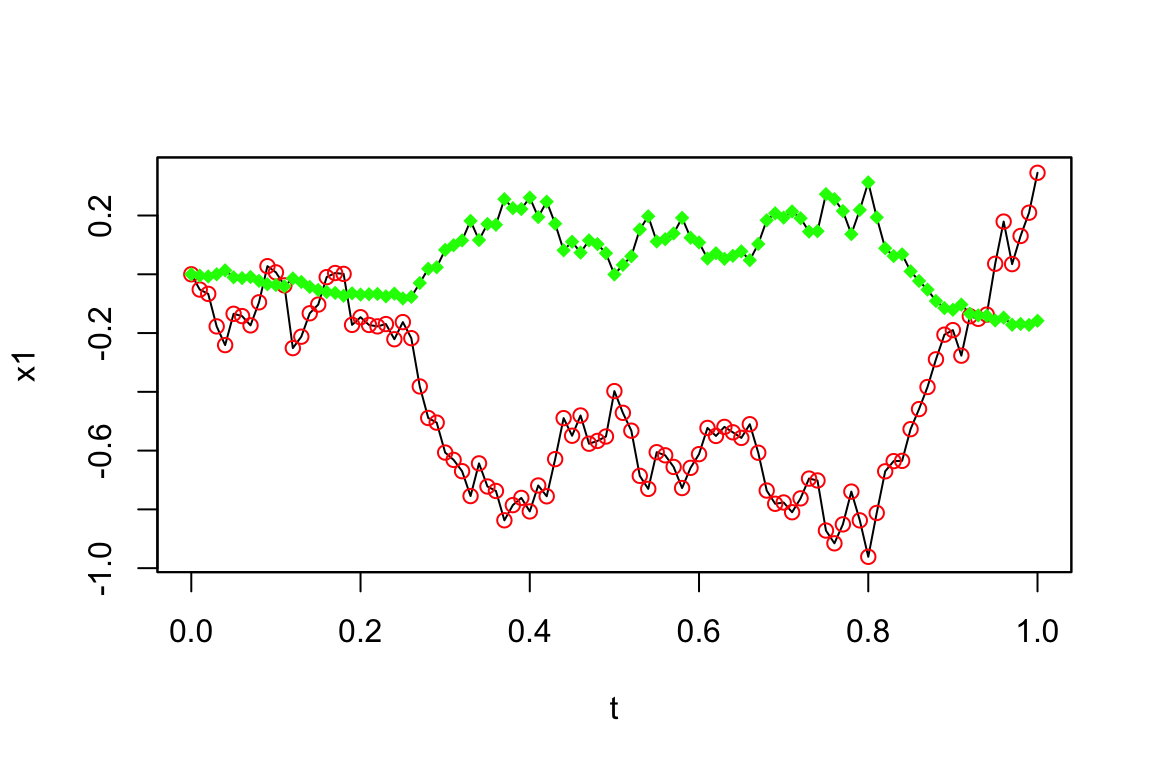

3.7 `zoo`との依存関係

zooというパッケージ (Zeileis and Grothendieck, 2005) が，時系列データを保存するために内部で用いられる．

より柔軟な時系列データの保存法ができたら，このdependencyは脱したいと考えられているようである．

4 漸近展開

確率変数の期待値を近似するのに，Monte Carlo法は普遍的な方法であるが，漸近展開もこれの代替手法である．精度さえ良ければ，計算時間は比較にならないほど速い．

4.1 場面設定

例えば，$d$-次元拡散過程 $X=(X^{(\epsilon)}_t)_{t\in[0,T]},\epsilon\in(0,1]$ を次のように定める： \[ X^{(\epsilon)}_t=x_0+\int^t_0a(X_s^{(\epsilon)},\epsilon)ds+\int^t_0b(X_s^{(\epsilon)},\epsilon)dW_s. \]

ただし，$W_t$ は $r$-次元Wiener過程とした．そして，その汎函数

\[ F^{(\epsilon)}=\sum_{\alpha=0}^r\int^T_0f_\alpha(X_t^{(\epsilon)},\epsilon)dW_t^\alpha+F(X_T^{(\epsilon)},\epsilon),\quad W^0_t=t \]

を決めたいとする．例えば，Black-Scholesモデル \[ dX_t^{(\epsilon)}=\mu X_t^{(\epsilon)}dt+\epsilon X_t^{(\epsilon)}dW_t \] において，利子率が零である場合のアジアオプションの価格は \[ \operatorname{E}\left[\max\left(\frac{1}{T}\int^T_0X_t^{(\epsilon)}dt-K,0\right)\right] \] と表せる（これは線型である）．これは \[ F^{(\epsilon)}=\frac{1}{T}\int^T_0X_t^{(\epsilon)}dt,\quad r=1 \] と定めた場合に相当する．また，$F^{(\epsilon)}=X^{(\epsilon)}_T$ とした場合に当たる \[ \operatorname{E}[(X^{(\epsilon)}_T-K)\lor0] \] がヨーロピアンコールオプションの価格になる．この値は閉じた形を持っているが，Asian optionについてはこの線型な設定においてさえ数値計算法が要請される．

4.2 渡部理論

ここでは，$\epsilon\searrow0$ の極限で系が決定論的であるとする．すなわち， \[ b(-,0)=0 \] \[ f_\alpha(-,0)=0\quad(\alpha\in[r]) \] とする．すると $X_t^{(0)}$ は次の常微分方程式 \[ \frac{d X_t^{(0)}}{d t}=a(X_t^{(0)},0),\quad X_0^{(0)}=x_0 \] の解であるから，$F^{(0)}$ も定数 \[ F^{(0)}=\int^T_0f_0(X_t^{(0)},0)dt+F(X_T^{(0)},0) \] で与えられる．

さらに，$a,b,f_\alpha,F$ がしかるべき正則性条件を満たすとき，汎函数 $F^{(\epsilon)}$ にはある版が存在して $\epsilon\in[0,1)$ に関して殆ど確実に滑らかである．特に， \[ \widetilde{F}^{(\epsilon)}:=\frac{F^{(\epsilon)}-F^{(0)}}{\epsilon} \] は次の確率展開を持つ： \[ \widetilde{F}^{(\epsilon)}\sim\widetilde{F}^{[0]}+\epsilon\widetilde{F}^{[1]}+\epsilon^2\widetilde{F}^{[2]}+\cdots\quad(\epsilon\searrow0) \]

この展開は，Malliavin解析のSobolev空間において厳密に成り立つ．これを導くのが (Watanabe, 1987) の理論である．

これに基づき，汎函数 $F^{(\epsilon)}$ の近似を構成する機能がyuimaに実装されている．この漸近展開をオプションの価格付けに応用したのが (Yoshida, 1992) である．

4.3 `setFunctional`コンストラクタ

Black-Scholesモデル \[ dX_t^{(\epsilon)}=\mu X_t^{(\epsilon)}dt+\epsilon X_t^{(\epsilon)}dW_t \] が定める幾何Brown運動 $(X_t)$ のパラメータが $\mu=1,x_0=1$ を満たす場合において，Asian call optionの価格は，汎函数 \[ g(x):=\max\left(F^{(0)}-K+\epsilon x,0\right) \] を計算すれば良い．

$F^{(\epsilon)}$ の極限 $F^{(0)}$ の値は，関数F0をyuima.functionalスロットが埋まったyuimaオブジェクトに適用することで得られる．

Code

model <- setModel(drift="x", diffusion=matrix("x*e", 1, 1))
K <- 100
yuima <- setYuima(model=model, sampling=setSampling(Terminal=1, n=1000))
yuima <- setFunctional(yuima, f=list(expression(x/T), expression(0)), F=0, xinit=150, e=0.5)
F0 <- F0(yuima)

Code

print(F0)

[1] 257.6134

Code

g <- function(x) {
  tmp <- (F0 - 100) + (0.5*x)
  tmp[(0.5*x) < (100-F0)] <- 0
  tmp
}
asymp <- asymptotic_term(yuima, block=10, expression(0), g)

Code

str(asymp)

List of 3
 $ d0: num 159
 $ d1: num -3.93
 $ d2: num [1, 1] 4

これを適切な和をとれば良い．

Code

e = 0.5
asy1 <- asymp$d0 + e*asymp$d1
asy2 <- asymp$d0 + e*asymp$d1 + e^2 * asymp$d2

はAsian call priceの，それぞれ1次と2次の漸近展開を与える．

4.4 CIR過程の推測

$X_t$ が幾何Brown運動の場合にしか (Levy, 1992) の近似は用いることはできない．例えばCIR模型 \[ dX_t=0.9X_tdt+\epsilon\sqrt{X_t}dW_t,\quad X_0=1, \] の場合でも，漸近展開は有効である．この状態でのEuropean call optionの価格は，2次までの漸近展開が与える値が，100万データ数によるMonte Carlo推定量の精度に匹敵し，当然計算量は圧倒的に少ない．

5 推論

ほとんどの手法が，$N\to\infty,\Delta_n\to0$ の極限で得られるデータ（高頻度データ）にも応用可能な手法になっている．

5.1 `setYuima`コンストラクタ

model, sampling のみから作れば，サンプリングをし，その結果をyuima.dataオブジェクトとして格納する．

一方で，dataをyuimaオブジェクトに持たせる方法でもある：

my.yuima <- setYuima(data=setData(myData), model=myModel)

data <- read.csv("http://chart.yahoo.com/table.csv?s=IBM&g=d&x=.csv")
x <- setYuima(data = setData(data$Close))
str(x@data)

5.2 擬似最尤推定⁹

$r$-次元Wiener過程 $\{W_t\}$ が定める拡散過程

\[ dX_t=a(X_t,\theta_2)dt+b(X_t,\theta_1)dW_t \]

のパラメータ $\theta_1\in\Theta_1\subset\mathbb{R}^p,\theta_2\in\Theta_2\subset\mathbb{R}^q$ の推定を考えたい．データ \[ \boldsymbol{X}_n:=(X_{t_i})_{i=0}^n,t_i:=i\Delta_n \] に関する対数尤度は次の擬似対数尤度を用いて近似できる：

\[ \ell_n(\boldsymbol{X}_n,\theta)=-\frac{1}{2}\sum_{i=1}^n\left(\log\det(\Sigma_{i-1}(\theta_1))+\frac{1}{\Delta_n}\Sigma_{i-1}^{-1}(\theta_1)\biggr((\Delta X_i-\Delta_na_{i-1}(\theta_2))^{\otimes 2}\biggl)\right) \] ただし \[ \Delta X_i:=X_{t_i}-X_{t_{i-1}},\Sigma_i(\theta_1):=\Sigma(\theta_1,X_{t_i}) \] \[ a_i(\theta_2):=a(X_{t_i},\theta_2),\Sigma:=b^{\otimes2},A^{\otimes2}:=AA^\top \] とした．これに対して \[ \widehat{\theta}:=\operatorname*{argmax}_{\theta}\ell_n(\boldsymbol{X}_n,\theta) \] と定めるのである．

実は，高頻度極限 $\Delta_n\to0,n\to\infty$ において，$\widehat{\theta}_1$ は漸近的に混合正規である (Genon-Catalot and Jacod, 1993)．$\widehat{\theta}_2$ も一致性を持つには，条件 $T=n\Delta_n\to\infty$ が必要である．これは $T$ が有限であるとき $\theta_2$ のFisher情報量も有限であり，それゆえこの設定したでは一致推定量が存在しないためである．$T\to\infty$ の下でエルゴード条件を仮定すれば，一致性だけでなく漸近正規性も達成される．局所Gauss近似を成立させるためには $n\Delta_n^2\to0$ が必要であるが，これでは条件が強すぎる．任意の $p\ge2$ に対して条件 $n\Delta_n^p\to0$ しか満たさない場合での適応的推定法が (Uchida and Yoshida, 2012) によって，大偏差原理による議論に基づいて提案された．

$T$ が大きくない場合， $\theta_2$ には小標本的な影響が現れる．これは適応的Bayes推定でも議論する．適応的Bayes事後平均推定量は，上述の $\widehat{\theta}_1,\widehat{\theta}_2$ と全く同じ漸近的性質を持つ．

これを実装するqmle関数が，stats4標準のmle関数に似せて作られている．

qmle(yuima, start, method = "L-BFGS-B", fixed = list(),
print = FALSE, envir = globalenv(), lower, upper, joint = FALSE, Est.Incr ="NoIncr",
aggregation = TRUE, threshold = NULL, rcpp =FALSE, ...)

startは最適化を始める初期値を，名前に対応づける辞書の形で与える．yuimaオブジェクトはmodelとdataのスロットが埋められていなければならない．最適化はBFGSによって行われる．

ジャンプ過程への応用も今後予定されている．

5.3 QMLEの例

例えば，次のモデル \[ dX_t=(2-\theta_2X_t)dt+(1+X_t^2)^{\theta_1}dW_t,\quad X_0=1, \] を考え，真値を $\theta_1=0.2,\theta_2=0.3$ としてデータを生成する．

Code

ymodel <- setModel(drift="(2-theta2*x)", diffusion="(1+x^2)^theta1")
n <- 750
ysamp <- setSampling(Terminal=n^(1/3), n=n)
yuima <- setYuima(model=ymodel, sampling=ysamp)
yuima <- simulate(yuima, xinit=1, true.parameter=list(theta1=0.2, theta2=0.3))

これに対して，QMLEを実行してみる：

Code

param.init <- list(theta2=0.5, theta1=0.5)
low.par <- list(theta1=0, theta2=0)
upp.par <- list(theta1=1, theta2=1)
mle1 <- qmle(yuima, start=param.init, lower=low.par, upper=upp.par)
summary(mle1)

Quasi-Maximum likelihood estimation

Call:
qmle(yuima = yuima, start = param.init, lower = low.par, upper = upp.par)

Coefficients:
        Estimate  Std. Error
theta1 0.2025147 0.006989654
theta2 0.2106767 0.108228544

-2 log L: -131.9554

$\theta_2$ の推定の方が圧倒的に難しいらしいことがよくわかる．

5.4 適応的Bayes推論

$r$-次元モデル

\[ dX_t=a(X_t,\theta_2)dt+b(X_t,\theta_1)dW_t \]

の擬似対数尤度

を考える．

まず，任意に初期値 $\theta^\star_2\in\Theta_2$ を取り，$\theta_1$ に事前分布 $\pi_1$ を導入して，これに基づいてBayes事後平均推定量を \[ \widetilde{\theta}_1:=\frac{\int_{\Theta_1}\theta_1\exp(\ell_n(\boldsymbol{X}_n,(\theta_1,\theta_2^\star)))\pi_1(\theta_1)d\theta_1}{\int_{\Theta_1}\exp(\ell_n(\boldsymbol{X}_n,(\theta_1,\theta_2^\star)))\pi_1(\theta_1)d\theta_1} \] と定める．$\pi_1$ は $\Theta_1$ 全域を台に持つならば，高頻度極限で良い漸近的性質を持つ．続いて，$\theta_2$ に事前分布 $\pi_2$ を導入して，$\widetilde{\theta}_1$ からBayes事後平均推定量を \[ \widetilde{\theta}_2:=\frac{\int_{\Theta_2}\theta_1\exp(\ell_n(\boldsymbol{X}_n,(\widetilde{\theta}_1,\theta_2)))\pi_2(\theta_2)d\theta_2}{\int_{\Theta_2}\exp(\ell_n(\boldsymbol{X}_n,(\widetilde{\theta}_1,\theta_2)))\pi_2(\theta_2)d\theta_2} \]

5.5 `adaBayes`の例

同様のモデル \[ dX_t=(2-\theta_2X_t)dt+(1+X_t^2)^{\theta_1}dW_t,\quad X_0=1, \] を考え，真値を $\theta_1=0.2,\theta_2=0.3$ としてデータを生成する．

Code

ymodel <- setModel(drift="(2-theta2*x)", diffusion="(1+x^2)^theta1")
n <- 750
ysamp <- setSampling(Terminal=n^(1/3), n=n)
yuima <- setYuima(model=ymodel, sampling=ysamp)
yuima <- simulate(yuima, xinit=1, true.parameter=list(theta1=0.2, theta2=0.3))

加えて，一様事前分布を用意する．

Code

prior <- list(theta2=list(measure.type="code", df="dunif(theta2,0,1)"),
      theta1=list(measure.type="code", df="dunif(theta1,0,1)"))
bayes1 <- adaBayes(yuima, start=param.init, prior=prior, mcmc=1000)
summary(bayes1)

  Length    Class     Mode 
       1 adabayes       S4

Code

summary(mle1)

Quasi-Maximum likelihood estimation

Call:
qmle(yuima = yuima, start = param.init, lower = low.par, upper = upp.par)

Coefficients:
        Estimate  Std. Error
theta1 0.2025147 0.006989654
theta2 0.2106767 0.108228544

-2 log L: -131.9554

Code

str(bayes1)

Formal class 'adabayes' [package "yuima"] with 6 slots
  ..@ mcmc       :List of 1
  .. ..$ : chr "NULL"
  ..@ accept_rate:List of 1
  .. ..$ : chr "NULL"
  ..@ coef       : Named num [1:2] 0.212 0.327
  .. ..- attr(*, "names")= chr [1:2] "theta1" "theta2"
  ..@ call       : language adaBayes(yuima = yuima, start = param.init, prior = prior, mcmc = 1000)
  ..@ vcov       : num [1:2, 1:2] 0 0 0 0
  ..@ fullcoef   : Named num [1:2] 0.212 0.327
  .. ..- attr(*, "names")= chr [1:2] "theta1" "theta2"

5.5.1 バグについて

coef(summary(bayes1))はエラーを生じる． > Error in object$coefficients : $ operator is invalid for atomic vectors > Calls: .main … eval_with_user_handlers -> eval -> eval -> coef -> coef -> coef.default
adaBayesの後ろの方に必須の引数mcmcがある．Manpageを読む限りiterationと同じ役割では？

5.5.2 小標本性がドリフト推定に与えるバイアス

ドリフト係数 $a(X_t,\theta_2)$ に関する推定は，$[0,T]$ の長さに強い影響を受けることが理論的にも知られている．数値実験では $n=750$ かつ \[ T=n^{\frac{1}{3}}\approx9.09 \] と取った．これをさらに $n=500,T\approx7.94$ とすると，

Code

n <- 500
ysamp <- setSampling(Terminal=n^(1/3), n=n)
yuima <- setYuima(model=ymodel, sampling=ysamp)
yuima <- simulate(yuima, xinit=1, true.parameter=list(theta1=0.2, theta2=0.3))
mle2 <- qmle(yuima, start=param.init, lower=list(theta1=0, theta2=0), upper=list(theta1=1, theta2=1))
bayes2 <- adaBayes(yuima, start=param.init, prior=prior, mcmc=1000)

Code

summary(mle2)

Quasi-Maximum likelihood estimation

Call:
qmle(yuima = yuima, start = param.init, lower = list(theta1 = 0, 
    theta2 = 0), upper = list(theta1 = 1, theta2 = 1))

Coefficients:
        Estimate Std. Error
theta1 0.2054158 0.02372179
theta2 0.9999339 0.29625725

-2 log L: -437.895

Code

str(bayes2)

Formal class 'adabayes' [package "yuima"] with 6 slots
  ..@ mcmc       :List of 1
  .. ..$ : chr "NULL"
  ..@ accept_rate:List of 1
  .. ..$ : chr "NULL"
  ..@ coef       : Named num [1:2] 0.21 0.719
  .. ..- attr(*, "names")= chr [1:2] "theta1" "theta2"
  ..@ call       : language adaBayes(yuima = yuima, start = param.init, prior = prior, mcmc = 1000)
  ..@ vcov       : num [1:2, 1:2] 0 0 0 0
  ..@ fullcoef   : Named num [1:2] 0.21 0.719
  .. ..- attr(*, "names")= chr [1:2] "theta1" "theta2"

小標本でも適応的Bayes推定量はよく振る舞う．一方で，QMLEでは劣化が激しい．$\widehat{\theta}_1$ は小標本の影響を $\widehat{\theta}_2$ ほどは大きく受けない．

5.6 非同期共分散推定¹⁰

伊藤過程が非同期に離散観測する設定を考える．

5.7 変化点解析¹¹

5.8 LASSOモデル選択¹²

6 Bayes推論

6.1 `adaBayes`モジュールについて

SDEモデル内のパラメータに対して適応的Bayes推論を実行するためのモジュールである．

R-Forge上のDocumentation
R-Forge上のSource
GitHub上のSource

References

Brouste, A., Fukasawa, M., Hino, H., Iacus, S., Kamatani, K., Koike, Y., … Yoshida, N. (2014). The YUIMA project: A computational framework for simulation and inference of stochastic differential equations. Journal of Statistical Software, 57(4), 1–51.

Genon-Catalot, V., and Jacod, J. (1993). On the estimation of the diffusion coefficient for multi-dimensional diffusion processes. Ananles de l’Institut Henri Poincaré, Probabilités Et Statistiques, 29(1).

Iacus, S. M. (2008). Simulation and inference for stochastic differential equations: With r examples. Springer New York.

Levy, E. (1992). Pricing european average rate currency options. Journal of International Money and Finance, 11(5), 474–491.

Uchida, M., and Yoshida, N. (2012). Adaptive estimation of an ergodic diffusion process based on sampled data. Stochastic Processes and Their Applications, 122(8), 2885–2924.

Watanabe, S. (1987). Analysis of wiener functionals (malliavin calculus) and its applications to heat kernels. The Annals of Probability, 15(1), 1–39.

Wood, A., and Chan, G. (1994). Simulation of stationary gaussian processes. Journal of Computational and Graphical Statistics, 3(4).

Yoshida, N. (1992). Asymptotic expansion for statistics related to small diffusions. Journal of the Japan Statistical Society, 22(2), 139–159.

Zeileis, A., and Grothendieck, G. (2005). Zoo: S3 infrastructure for regular and irregular time series. Journal of Statistical Software, 14(6), 1–27.

Footnotes

(Brouste et al., 2014) 第７節も参照．↩︎
(Brouste et al., 2014) 概要より．↩︎
R-Forge とは，SourceForge に似た，R 言語のパッケージ開発者向けの協力的な開発環境を提供するプラットフォーム．↩︎
rdrr は CRAN や GitHub だけでなく，Bioconductor や R-Forge も含めて検索可能にしているサイト．↩︎
ただし，marmaidの記法としてクラス名に.を許さないので，yuima.modelの代わりに図中ではyuima_modelと記述している．↩︎
モデルの左辺 $dX_t$ はyuima.modelのスロットsolve.variableがstate.variableに暗黙のうちに一致させているところから暗黙に読み込んでいる．↩︎
(Brouste et al., 2014) 第3.4節 pp.12-13．↩︎
ただし，分数Gaussノイズが仮定された場合はCholesky法または (Wood and Chan, 1994) の手法による．↩︎
(Brouste et al., 2014, p. 第6.2節)↩︎
(Brouste et al., 2014, p. 第6.4節)↩︎
(Brouste et al., 2014, p. 第6.5節)↩︎
(Brouste et al., 2014, p. 第6.6節)↩︎

1 YUIMAとは？

2 YUIMAの構造とモデル定義

2.1 クラス構造

2.2 setModel()コンストラクタ

2.3 1次元の場合

2.4 多次元の場合

2.5 分数Gaussなノイズ

2.6 Lévy過程

3 シミュレーションとサンプリング

3.1 simulate()関数の使い方

3.2 時間離散化Euler-Maruyama法

3.3 空間離散Euler-Maruyama法

3.4 setSamplingコンストラクタ

3.5 subsampling関数の使い方

3.6 サンプリングとサブサンプリングの組み合わせ

3.7 zooとの依存関係

4 漸近展開

4.1 場面設定

4.2 渡部理論

4.3 setFunctionalコンストラクタ

4.4 CIR過程の推測

5 推論

5.1 setYuimaコンストラクタ

5.2 擬似最尤推定9

5.3 QMLEの例

5.4 適応的Bayes推論

5.5 adaBayesの例

5.5.1 バグについて

5.5.2 小標本性がドリフト推定に与えるバイアス

5.6 非同期共分散推定10

5.7 変化点解析11

5.8 LASSOモデル選択12

6 Bayes推論

6.1 adaBayesモジュールについて

References

Footnotes

2.2 `setModel()`コンストラクタ

3.1 `simulate()`関数の使い方

3.4 `setSampling`コンストラクタ

3.5 `subsampling`関数の使い方

3.7 `zoo`との依存関係

4.3 `setFunctional`コンストラクタ

5.1 `setYuima`コンストラクタ

5.2 擬似最尤推定⁹

5.5 `adaBayes`の例

5.6 非同期共分散推定¹⁰

5.7 変化点解析¹¹

5.8 LASSOモデル選択¹²

6.1 `adaBayes`モジュールについて