PDMPFlux.jl Package for the New Era of MCMC

新時代の MCMC 環境に向けて：PDMPFlux.jl

Hirofumi Shiba

10/29/2024

1 Introduction

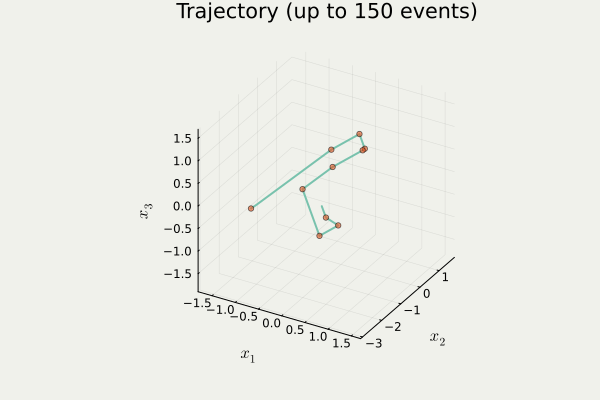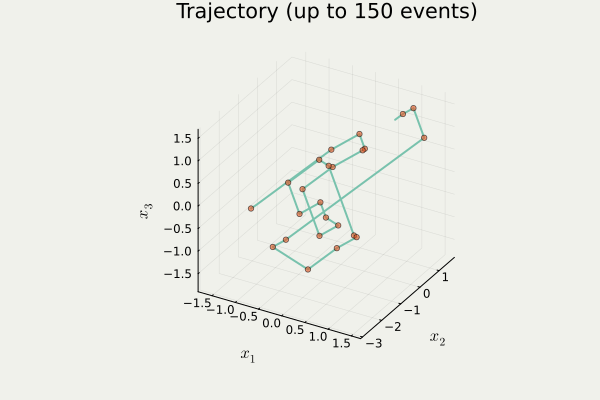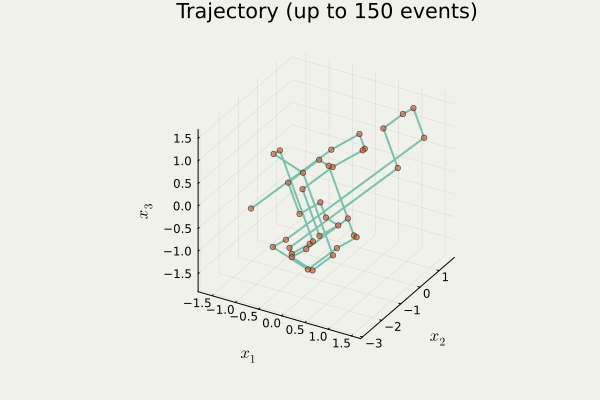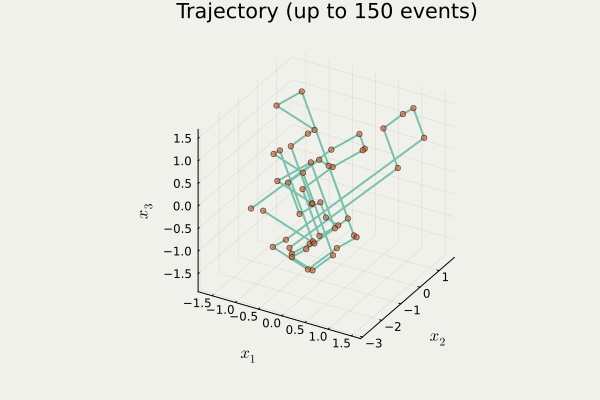
Output from anim_traj() in PDMPFlux.jl package

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1.1 Overview

PDMPFlux.jl: package for MCMC sampling.

1.2 What’s Different? (Detailed in Section 2)

Instead of Markov Chains, PDMPFlux.jl uses:

Currently, most PDMPs move piecewise linearly.

1.3 What’s PDMP? (Detailed in Section 2)

	PDMP	Diffusion
Diffuse?	No	Yes
Jump?	Yes	No
Driving noise	Poisson	Gauss
Plot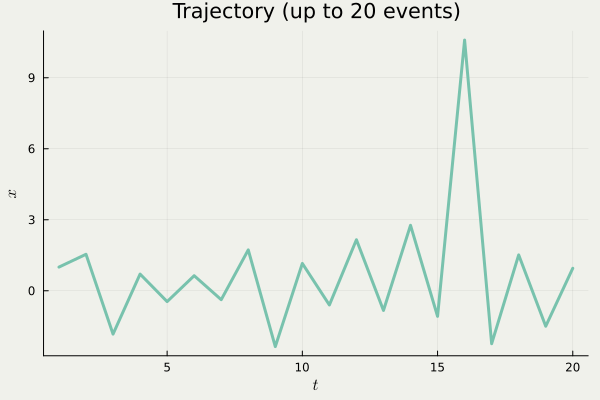

1.4 How to Use? (1/3)

using PDMPFlux

function U_Cauchy(x::Vector)
    return log(1 + x.^2)
end

dim = 10
sampler = ZigZagAD(dim, U_Cauchy)  # Instantiate a sampler

Inputs: Dimension d, and any U that satisfies

p(x) \,\propto\,\exp\left\{ -U(x) \right\},\qquad x\in\mathbb{R}^d.

U may be called potential, or negative log-density.

1.5 How to Use? (2/3)

N_sk, N, xinit, vinit = 1_000_000, 1_000_000, zeros(dim), ones(dim)  # Hyperparameters
samples = sample(sampler, N_sk, N, xinit, vinit, seed=2024)

Output: N samples from p\,\propto\,e^{-U}.

N_sk: number of orange points, N: number of samples, xinit, vinit: initial position and velocity.

1.6 How to Use? (3/3)

Function sample is a wrapper of:

traj = sample_skeleton(sampler, N_sk, xinit, vinit)  # simulate skeleton points
samples = sample_from_skeleton(sampler, N, traj)  # get samples from the skeleton points

traj contains a list \{x_i\}_{i=1}^{N_{sk}} of orange points

1.7 Diagnostic

diagnostic(traj)

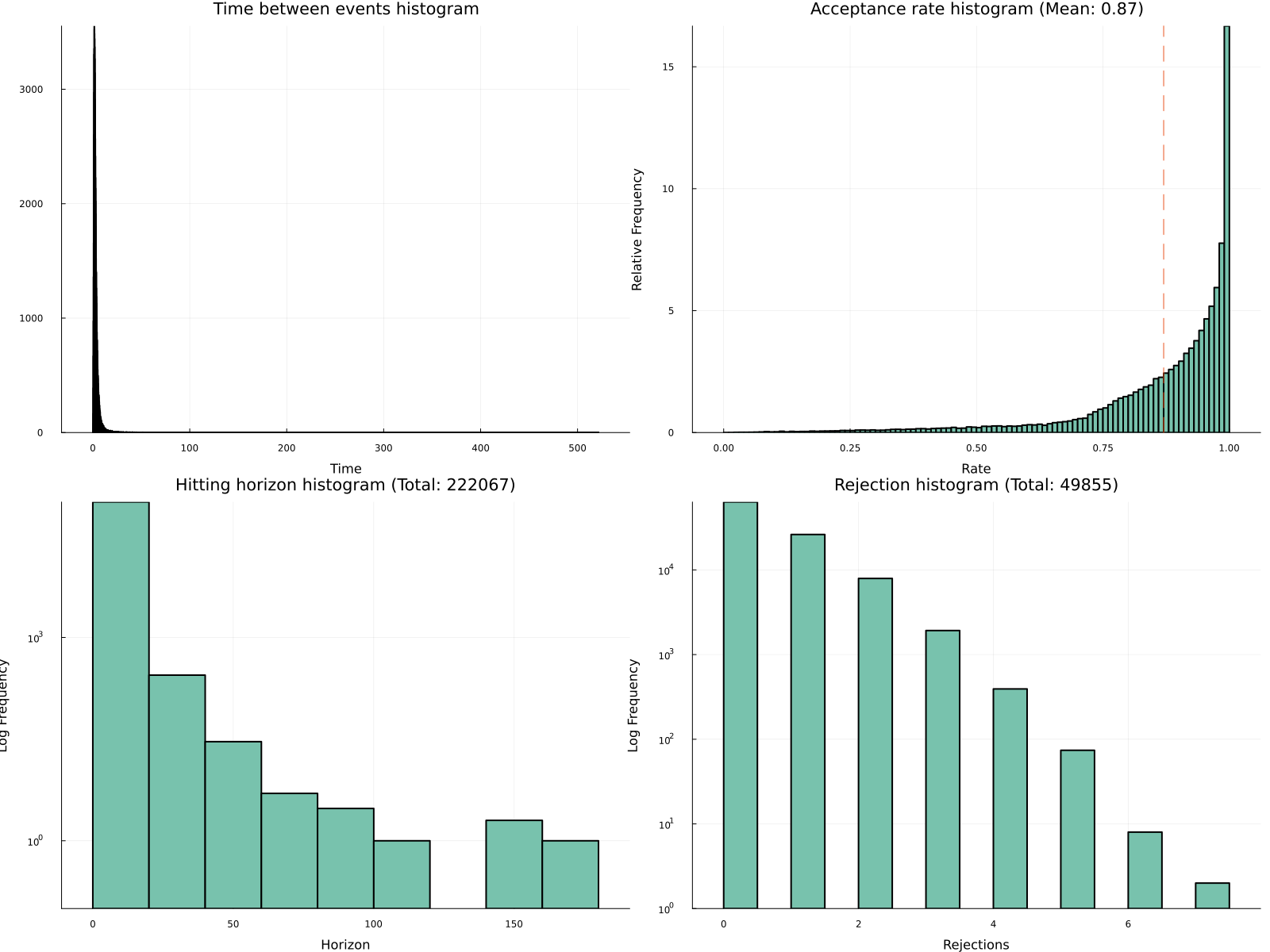
We see acceptance rate is a bit low due to the long tails of p.

2 What is PDMP?

Animated by (Grazzi, 2020)

2.1 Two Key Changes in MCMC History

1. Lifting: MH (Metropolis-Hastings) → Lifted MH
2. Continuous-time Limit: Lifted MH → Zig-Zag Sampler

(MH Metropolis et al., 1953)

(Lifted MH Turitsyn et al., 2011)

(Zig-Zag Bierkens et al., 2019)

2.2 What’s Wrong with MH?: Reversibility

Reversibility (a.k.a detailed balance): p(x)q(x|y)=p(y)q(y|x). In words: \text{Probability}[\text{Going}\;x\to y]=\text{Probability}[\text{Going}\;y\to x]. Harder to explore the entire space

Slow mixing of MH

2.3 Lifting into a Larger State Space

q^{(+1)}: Only propose \rightarrow moves

q^{(-1)}: Only propose \leftarrow moves

Once going uphill, it continues to go uphill.

This is irreversible, since

\begin{align*} &\text{Probability}[x\to y]\\ &\qquad\ne\text{Probability}[y\to x]. \end{align*}

2.4 Continuous-time Limit: A Strategy for Efficient Computing

‘Limiting case of lifted MH’ means that we only simulate where we should flip the momentum \sigma\in\{\pm1\} in Lifted MH.

(1d Zig Zag sampler Bierkens et al., 2019)

Input: Gradient \nabla\log p of log target density p

For n\in\{1,2,\cdots,N\}:

1. Simulate an first arrival time T_n of a Poisson point process (described in the next slide)
2. Linearly interpolate until time T_n: X_t = X_{T_{n-1}} + \sigma(t-T_{n-1}),\qquad t\in[T_{n-1},T_n].
3. Go back to Step 1 with the momentum \sigma\in\{\pm1\} flipped

2.5 Summary

1. PDMPs have irreversible dynamics
2. PDMPs are easy to simulate
3. Promising for high-dimensional problems

Using PDMPFlux.jl, I want to fit a large Bayesian model, showcasing the usefulness of PDMP samplers.

3 References

For further details, please see my old introductory slides via the above QR code

Bierkens, J., Fearnhead, P., and Roberts, G. (2019). The Zig-Zag Process and Super-Efficient Sampling for Bayesian Analysis of Big Data. The Annals of Statistics, 47(3), 1288–1320.

Grazzi, S. (2020). Piecewise deterministic monte carlo.

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E. (1953). Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6), 1087–1092.

Turitsyn, K. S., Chertkov, M., and Vucelja, M. (2011). Irreversible Monte Carlo algorithms for Efficient Sampling. Physica D-Nonlinear Phenomena, 240(5-Apr), 410–414.