Gauss 過程を用いた統計解析

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

Gauss 過程を用いた推論を実行するライブラリには，Matlab パッケージである GPML や，Python における GPy がある．

理論編も参照（画像をタップでリンクを開く）

1 Gauss 過程回帰（実践）

1.1 扱うデータ¹

データ $x_1,\cdots ,x_N,N=100$ として，$\mathrm{N}(0,{0.8}^2)$ に従う乱数を用意する．これに対して， $$y_i=\sin (3x_i)+ϵ,$$ $$ϵ\sim \mathrm{N}(0,{0.09}^2),$$ を通じて $y_1,\cdots ,y_N$ を生成する．

import numpy as np

N = 10

np.random.seed(1234)

x = np.random.randn(N,1) * 0.8

y = np.sin(3*x) + np.random.randn(N,1) * 0.09

xs = np.linspace(-3,3,61).reshape(-1,1)

この非線型関数 $\sin$ を，Gauss 過程回帰がどこまで復元できるかが実験の主旨である．

1.2 GPy を用いた場合

GPy を用いて Gauss 過程回帰を行うには，GPy.models.gp_regression モジュールの GPRegression クラス

class GPRegression(X, Y, kernel=None, Y_metadata=None, normalizer=None, noise_var=1.0, mean_function=None)

を用いる．ソースコードは こちら．

引数のカーネル kernel は PGPy kernel オブジェクトを取り，デフォルトは rbf カーネルである．我々も RBF カーネル を用いることとする．これは GPy パッケージでは GPy.kern.src.rbf モジュールの RBF クラスで提供されている：

class RBF(input_dim, variance=1.0, lengthscale=None, ARD=False, active_dims=None, name='rbf', useGPU=False, inv_l=False)

ソースコードは こちら．

モデルオブジェクトを初期化した後は次のように進む

1. optimize メソッド でハイパーパラメータを最適化する．

   optimize(optimizer=None, start=None, messages=False, max_iters=1000, ipython_notebook=True, clear_after_finish=False, **kwargs)

   これはインスタンスの self.log_likelihood と self.log_likelihood_gradient を用いて，負の対数尤度を最小化する形で行われる．

2. predict メソッド でテスト点での予測を行う．

   predict(Xnew, full_cov=False, Y_metadata=None, kern=None, likelihood=None, include_likelihood=True)

   返り値は事後平均と事後分散を numpy.ndarray として返す．

3. matplotlib を用いて予測の結果をプロットする．

import GPy
import matplotlib.pyplot as plt

kernel = GPy.kern.RBF(input_dim=1, variance=1.0)
model = GPy.models.GPRegression(x, y, kernel)

model.optimize()
mu, var = model.predict(xs)

# テスト点での平均と95%信頼区間のプロット
upper = mu + 1.96*np.sqrt(var)
lower = mu - 1.96*np.sqrt(var)
plt.fill_between(xs[:,0], lower[:,0], upper[:,0], color='lightgray', label='95% confidence interval', alpha=0.5)
plt.plot(xs, mu, label='Predicted mean')
plt.scatter(x, y, c='r', label='Observations', s=10)
plt.legend()

plt.show()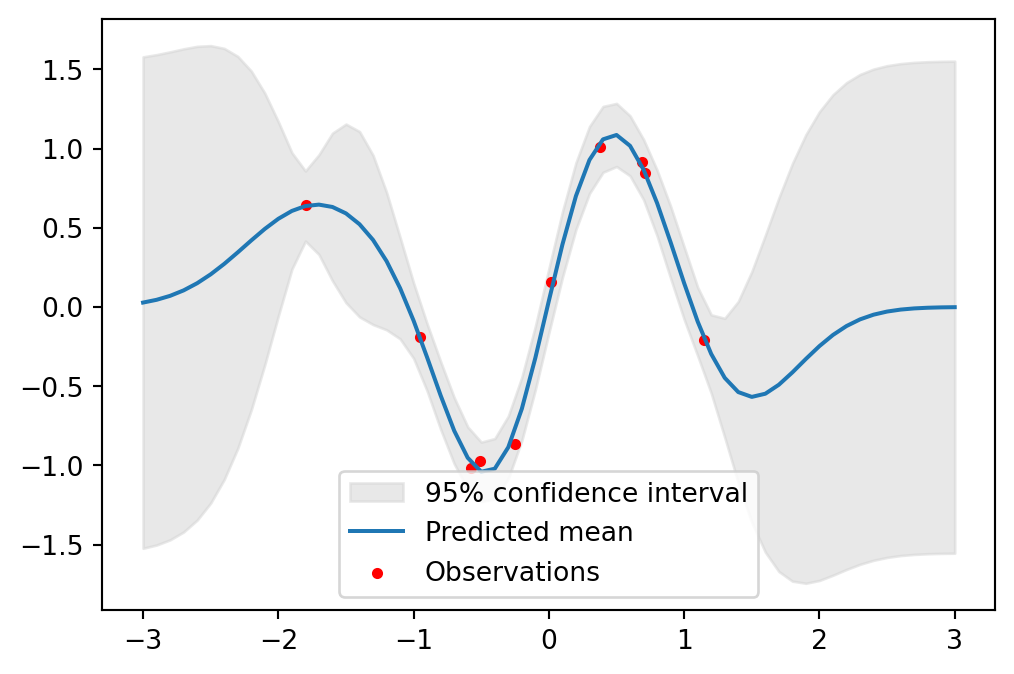

import numpy as np
import GPy
import matplotlib.pyplot as plt

kernel = GPy.kern.RBF(input_dim=1, variance=1.0)
model = GPy.models.GPRegression(x, y, kernel)
model.optimize()

xs = np.linspace(x.min(), x.max(), 1000)[:, None]
mu, var = model.predict(xs)

upper = mu + 1.96 * np.sqrt(var)
lower = mu - 1.96 * np.sqrt(var)

fig, ax = plt.subplots(figsize=(6, 4))  # グラフサイズを小さく

# 背景を白に
ax.set_facecolor('white')

# グラフ領域を削除
ax.patch.set_visible(False)

# 軸を細く
ax.spines['bottom'].set_linewidth(0.5)
ax.spines['left'].set_linewidth(0.5)

# メモリを非表示
ax.tick_params(axis='both', which='both', length=0, labelleft=False, labelbottom=False, left=False, bottom=False)

# 軸ラベルを削除
ax.set_xlabel('')
ax.set_ylabel('')

# 凡例を非表示
ax.legend().set_visible(False)

# データプロット
ax.fill_between(xs[:, 0], lower[:, 0], upper[:, 0], color='lightgray', alpha=0.5)
ax.plot(xs[:, 0], mu[:, 0], color='k', lw=1)
ax.scatter(x[:, 0], y[:, 0], c='b', s=30)

plt.tight_layout(pad=0.2)
plt.show()

 /var/folders/gx/6w78f6997l5___173r25fp3m0000gn/T/ipykernel_9031/3363038710.py:35: UserWarning:No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.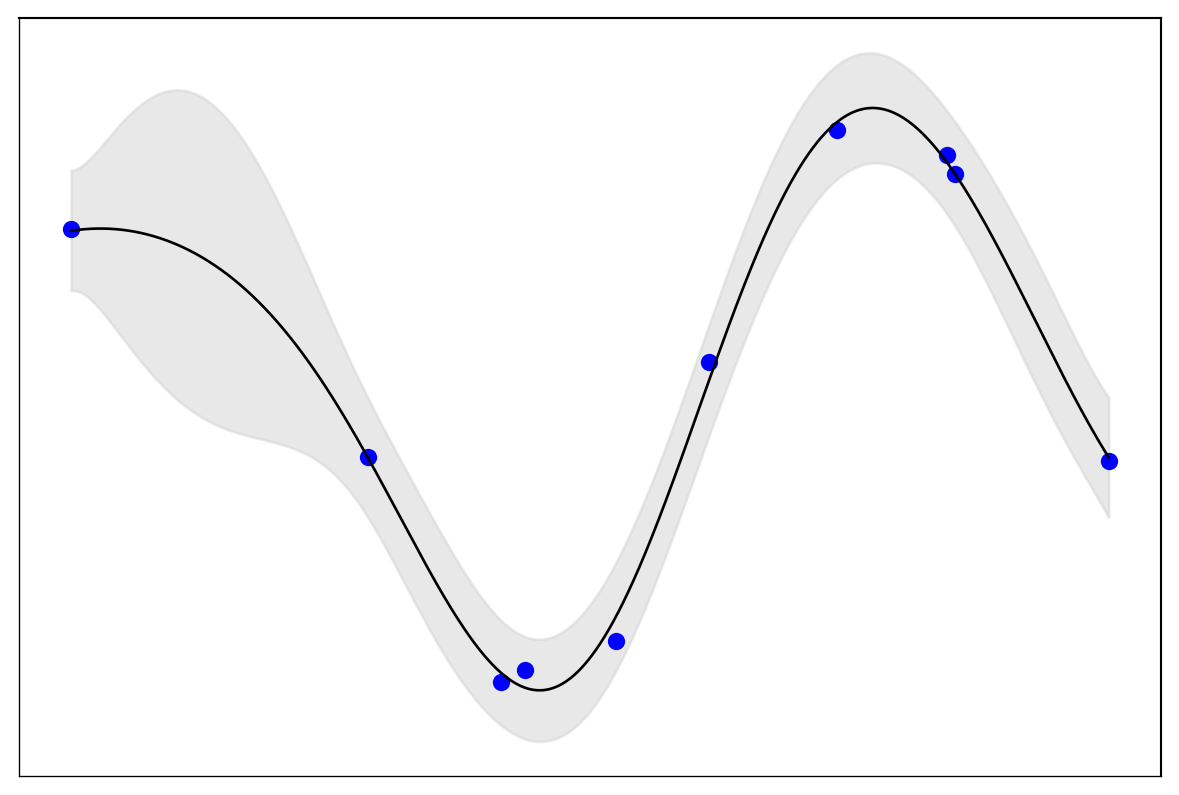

特に $[-2,2]$ の区間において，元の関数 $\sin$ をよく復元できていることが分かる．実際，$y=\sin (3x)$ と重ねてプロットすると次の通り：

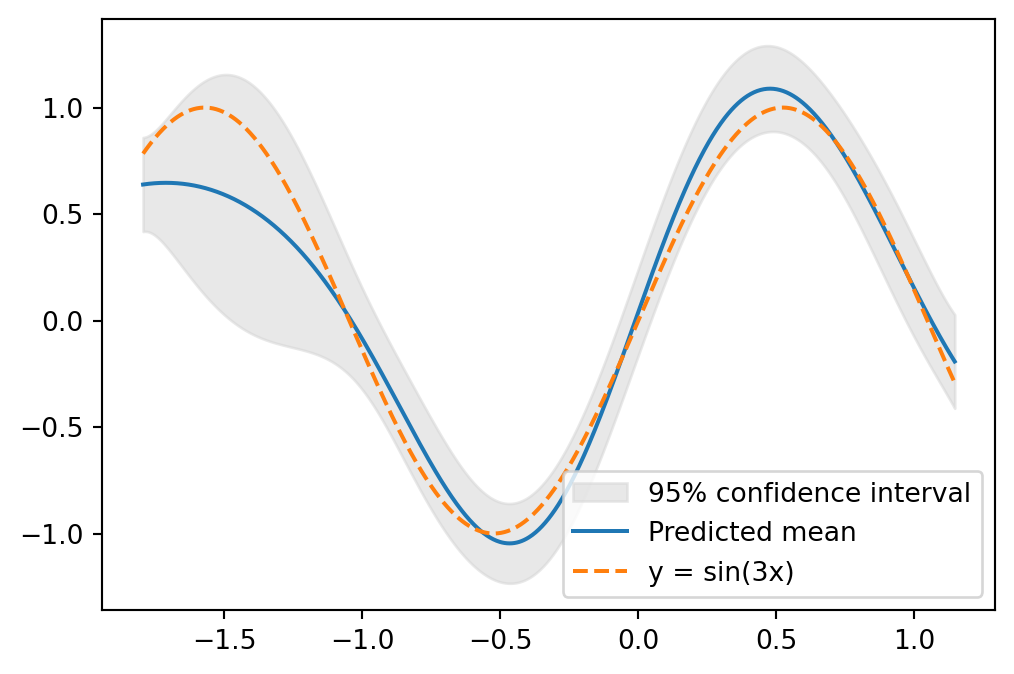
1.3 scikit-learn を用いた場合

補足：scikit-learn における Gauss 過程回帰

このような単純な解析では，scikit-learn と用いるとより同じ分析が実行できる．

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C
import numpy as np
import matplotlib.pyplot as plt

kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))

gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10, alpha=0.1)

# モデルの学習
gp.fit(x, y.ravel())

mu, s2 = gp.predict(xs, return_std=True)

# テスト点での平均と95%信頼区間のプロット
plt.fill_between(xs.ravel(), mu - 1.96 * s2, mu + 1.96 * s2, color='lightgray', label='95% confidence interval', alpha=0.5)
plt.plot(xs, mu, label='Predicted mean')
plt.scatter(x, y, c='r', label='Observations', s=10)
plt.legend()
plt.show()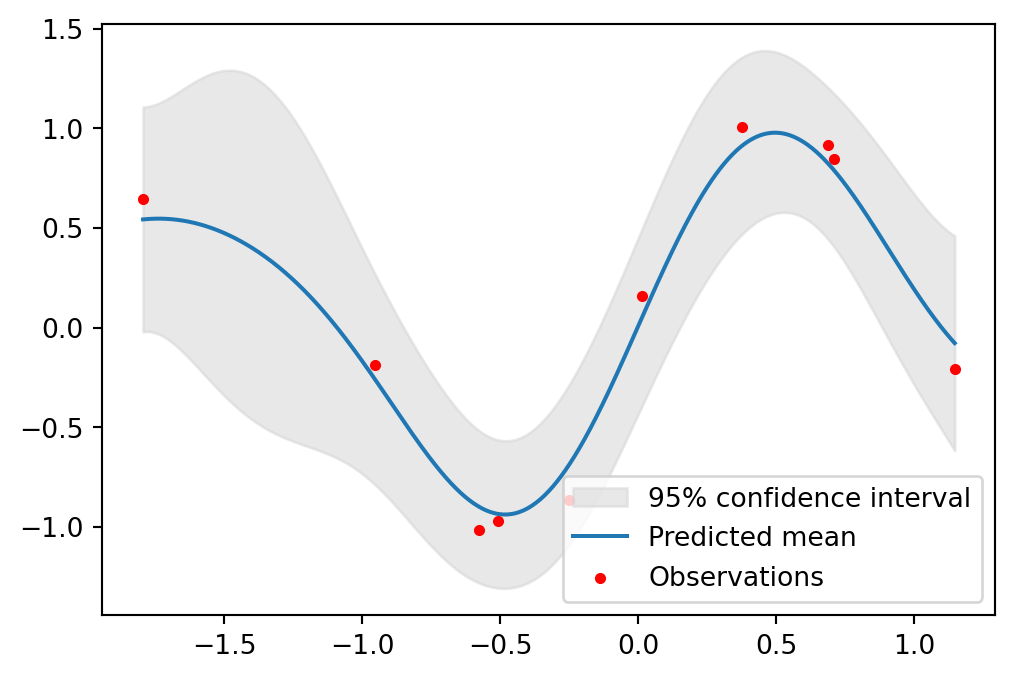

2 Gauss 過程による分類²

本質的には Gauss 過程回帰と変わらないが，回帰の場合と変え得る．

2.1 扱うデータ

ここでは， $$m_1:=\left(\begin{array}{c}3/4\\ 0\end{array}\right),m_2:=\left(\begin{array}{c}-3/4\\ 0\end{array}\right),$$ $${\mathrm{\Sigma }}_1:=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),{\mathrm{\Sigma }}_2:=\left(\begin{array}{cc}1& 0.95\\ 0.95& 1\end{array}\right),$$ とし，${\mathrm{N}}_2(m_1,{\mathrm{\Sigma }}_1)$ から $n_1:=320$ データ，${\mathrm{N}}_2(m_2,{\mathrm{\Sigma }}_2)$ から $n_2:=160$ データを生成する：

n1, n2 = 320, 160
S1 = np.eye(2)
S2 = np.array([[1, 0.95], [0.95, 1]])
m1 = np.array([0.75, 0])
m2 = np.array([-0.75, 0])

x1 = np.random.multivariate_normal(m1, S1, n1)
x2 = np.random.multivariate_normal(m2, S2, n2)

x = np.vstack((x1, x2))

y1 = -np.ones(n1)
y2 = np.ones(n2)
y = np.concatenate((y1, y2)).reshape(-1,1)

plt.plot(x1[:, 0], x1[:, 1], 'o', label='Class 1')
plt.plot(x2[:, 0], x2[:, 1], '*', label='Class 2')
plt.legend()
plt.show()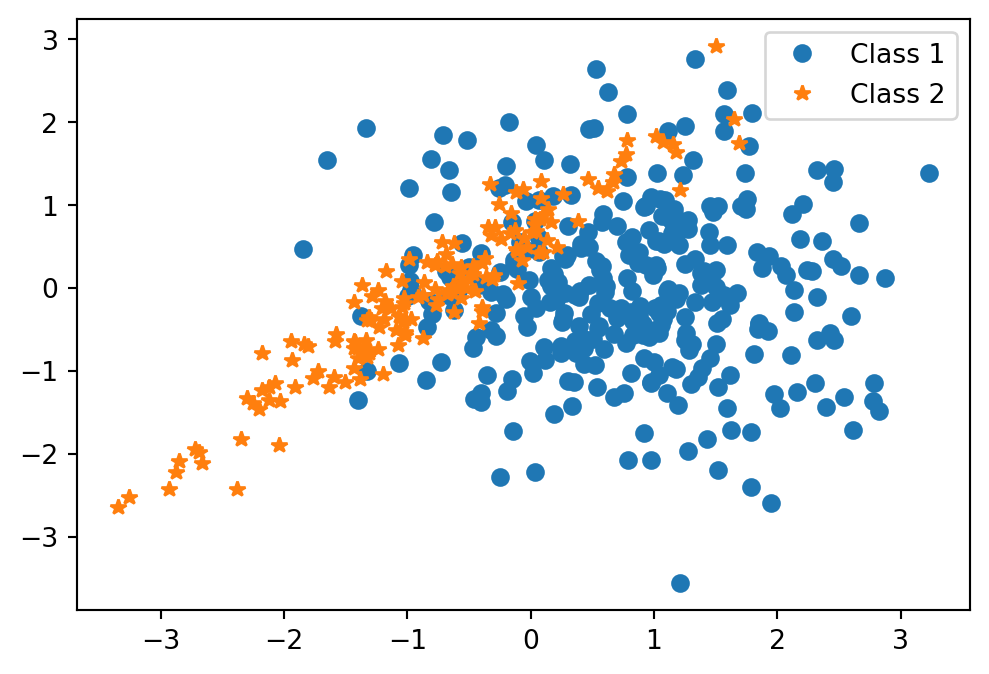

1

クラスラベルは $\{\pm 1\}$ であることに注意．

図 1

$n_1:n_2=2:1$ であるから，このデータは Gauss 混合モデル $$\begin{array}{}\text{(1)}& \frac{2}{3}\varphi (x;m_1,{\mathrm{\Sigma }}_1)+\frac{1}{3}\varphi (x;m_2,{\mathrm{\Sigma }}_2)\end{array}$$ からのデータと見れる．ただし，$\varphi (x;m,\mathrm{\Sigma })$ は ${\mathrm{N}}_2(\mu ,\mathrm{\Sigma })$ の密度関数とした．

サンプリング点は $[-4,4{]}^2$ 内の幅 $0.1$ の格子点とする：

t1, t2 = np.meshgrid(np.arange(-4, 4.1, 0.1), np.arange(-4, 4.1, 0.1))
t = np.column_stack([t1.flat, t2.flat])

点 $x$ でモデル 1 からのデータが観測されたとき，これがクラス $1,2$ からのものである確率 $p_1,p_2$ は $$\begin{array}{rl}{p}_1& =\frac{n_1}{n_1+n_2}\varphi (x;m_1,{\mathrm{\Sigma }}_1)\\ & =\frac{1}{2\pi (n_1+n_2)}\cdot n_1\frac{e^{-\frac{1}{2}(x-m_1{)}^{\mathrm{\top }}{\mathrm{\Sigma }}_1^{-1}(x-m_1)}}{\sqrt{det{\mathrm{\Sigma }}_1}}\end{array}$$ $$p_2=\frac{1}{2\pi (n_1+n_2)}\cdot n_2\frac{e^{-\frac{1}{2}(x-m_2{)}^{\mathrm{\top }}{\mathrm{\Sigma }}_2^{-1}(x-m_2)}}{\sqrt{det{\mathrm{\Sigma }}_2}}$$ である．

よって，$x\in [-4,4{]}^2$ がクラス $2$ からのものである確率を，等高線 (contour) としてプロットすると，次の通りになる：

invS1 = np.linalg.inv(S1)
invS2 = np.linalg.inv(S2)
detS1 = np.linalg.det(S1)
detS2 = np.linalg.det(S2)

tmm1 = t - m1
p1 = n1 * np.exp(-0.5 * np.sum(tmm1.dot(invS1) * tmm1, axis=1)) / np.sqrt(detS1)

tmm2 = t - m2
p2 = n2 * np.exp(-0.5 * np.sum(tmm2.dot(invS2) * tmm2, axis=1)) / np.sqrt(detS2)

posterior = p2 / (p1 + p2)

# 等確率等高線のプロット
contour_levels = np.arange(0.1, 1, 0.1)
plt.contour(t1, t2, posterior.reshape(t1.shape), levels=contour_levels)

# データポイントのプロット
plt.plot(x1[:, 0], x1[:, 1], 'o', label='Class 1', alpha=0.5)
plt.plot(x2[:, 0], x2[:, 1], '*', label='Class 2', alpha=0.5)
plt.legend()
plt.show()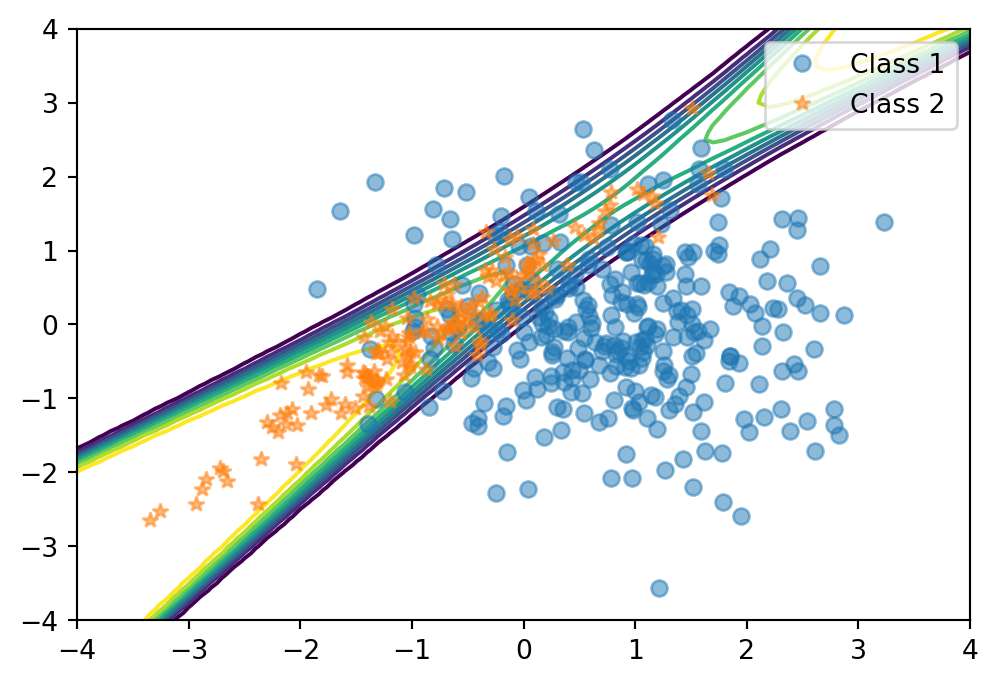

2.2 モデル

平均は $0$ とし，共分散関数は 関連度自動決定 (ARD: Autonatic Relevance Determination) (MacKay, 1994), (Neal, 1996, p. 16) を用いる．

これは，２つの入力 $x_1,x_2$ が異なる重要度を持つ場合，それぞれの入力に対するスケールパラメータを導入する手法である．

これは，GPy.kern.RBF 関数のキーワード引数 ARD=True を通じて実装できる：

import time

start_time = time.time()

meanfunc = GPy.mappings.Constant(2,1)
kernel = GPy.kern.RBF(input_dim=2, ARD=True)

model = GPy.models.GPClassification(x, y, kernel=kernel, mean_function=meanfunc)
model.optimize()

# テストデータセットに対する予済分布の計算
y_pred, _ = model.predict(t)

end_time = time.time()

# 予測確率の等高線プロット
plt.figure(figsize=(8, 6))
plt.plot(x1[:,0], x1[:,1], 'o', label='Class 1', alpha=0.5)
plt.plot(x2[:,0], x2[:,1], '*', label='Class 2', alpha=0.5)
contour = plt.contour(t1, t2, y_pred.reshape(t1.shape), levels=np.linspace(0, 1, 10))
plt.clabel(contour, inline=1, fontsize=10)
plt.legend()
plt.show()

elapsed_time = end_time - start_time
print(f"実行時間: {elapsed_time:.1f} 秒")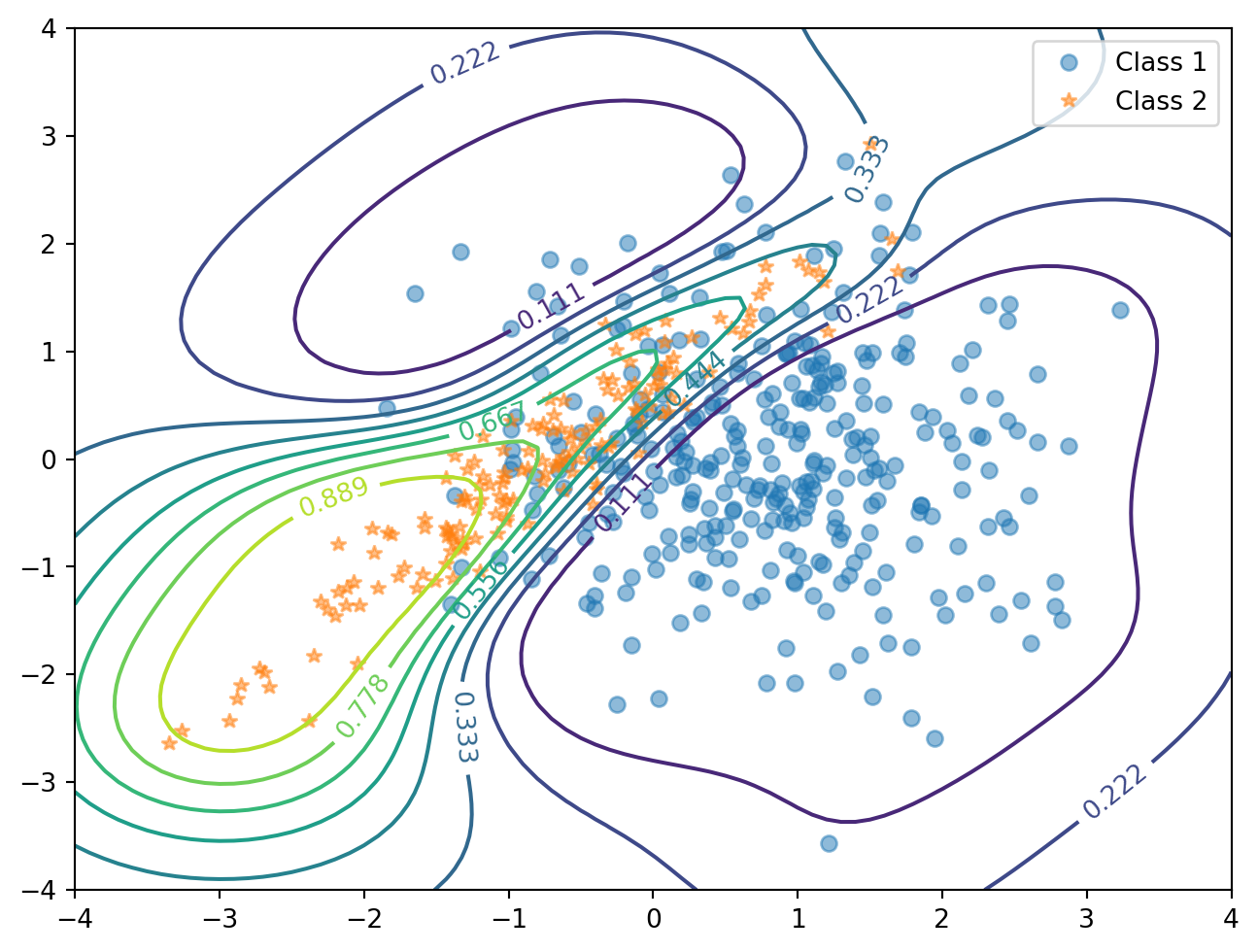

実行時間: 14.3 秒

図 1 の真の構造の特徴を捉えていることが判る．

References

MacKay, D. J. C. (1994). Bayesian nonlinear modeling for the prediction competition (No. 2),Vol. 100. American Society of Heating, Refrigerating,; Air Conditioning Engineers (ASHRAE). Retrieved from https://www.osti.gov/biblio/33309

Neal, R. M. (1996). Bayesian learning for neural networks,Vol. 118. Springer New York.

Footnotes

1. Documentation for GPML Matlab Code version 4.2 3c 節を参考にした．

2. Documentation for GPML Matlab Code version 4.2 4e 節を参考にした．