動き出す次世代サンプラー

区分確定的モンテカルロ

スライドはこちら． 予稿はこちら．

Slide
PDMP
Julia
Author
Affiliation

司馬博文

総合研究大学院大学（５年一貫博士課程）２年

Published

2/06/2025

概要

統計数理研究所２階大会議室． スライドはこちら．予稿はこちら．

1 区分確定的マルコフ過程 PDMP

モンテカルロ法に用いられる PDMP の例．発表者開発の PDMPFlux.jl パッケージからの出力．

1.1 モンテカルロ法３分類

Markov 連鎖

拡散過程

PDMP

1.2 Piecewise Deterministic Markov Process

1.3 モンテカルロ法小史 1/2

1.4 モンテカルロ法小史 2/2

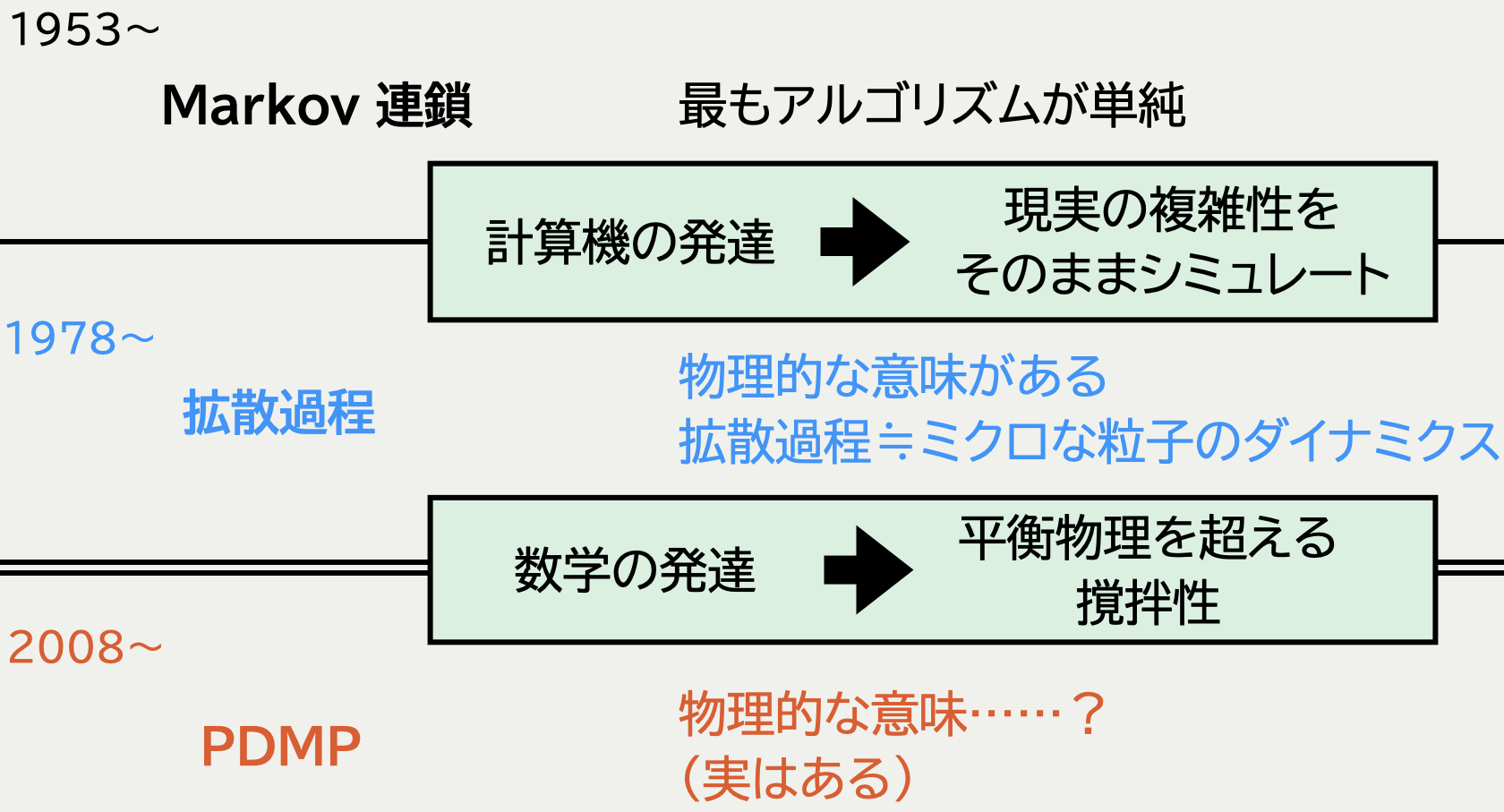
1.5 拡散過程の何がダメなのか？

物理のくびき

  • 拡散過程は孤立系の平衡ダイナミクス

    例：コーヒーの中に入れた砂糖粒子

  • 必ずしもこれを模倣する必要はない．

    例：コーヒーに砂糖を入れたあと混ぜずに見つめている人はいない

アルゴリズムのくびき

  • 拡散過程は正確にシミュレートできない．

    離散化をし，数値誤差を Metropolis-Hastings ステップで補正する．

    アルゴリズムが重くなる．

1.6 PDMP の何が良いのか？

物理：非可逆なダイナミクス

  • 「棄却」されるまで一直線に猛進

    ≒ スプーンで混ぜる行為の模倣

  • 人工的な対称性（例：詳細釣り合い）がない

    収束が速い (Diaconis, 2013),
    (Andrieu and Livingstone, 2021)

アルゴリズム：棄却フリー

  • PDMP は数値誤差なくシミュレートできる

    Metropolis-Hastings の棄却-採択の枠組みが要らない

1.7 PDMP の何が難しいのか？

物理：非可逆なダイナミクス

  • 「棄却」されるまで一直線に猛進

    ≒ スプーンで混ぜる行為の模倣

  • 人工的な対称性（例：詳細釣り合い）がない

    問題ごとにアルゴリズムを設計する必要
    汎用パッケージがない

アルゴリズム：棄却フリー

  • PDMP は数値誤差なくシミュレートできる

    Metropolis-Hastings の棄却-採択の枠組みが要らない

1.8 初の PDMP 汎用パッケージ

Python パッケージ（Charly Andral） 

pip install pdmp-jax

Julia パッケージ（申請者開発） 

] add PDMPFlux

1.9 PDMP の例 1/2 （申請者開発のパッケージより）

(Bouchard-Côté et al., 2018)

(Bierkens et al., 2019)

(Bierkens et al., 2020)

1.10 PDMP の例 2/2 （申請者開発のパッケージより）

(Michel et al., 2020)

(Vasdekis and Roberts, 2023)

(Bierkens et al., 2023)

このあとの内容

  • 第１節：区分確定的マルコフ過程 PDMP （終わった）
    • PDMPFlux パッケージの紹介
  • 第２節：PDMP のシミュレーションと課題 これから
    • ○ データの一部を見るだけで実行可能（スケーラビリティ）
    • 自動化・汎用化することが難しい
  • 第３節：本パッケージの実装
    • 鍵となる技術：自動微分のベクトライズ

2 PDMP のシミュレーションと課題

PDMP のシミュレーション＝緑色の点をどう打つか？

2.1 課題：非一様 Poisson 点過程のシミュレーション

PDMP シミュレーションの原則

方向転換地点 \textcolor{#78C2AD}{x_1,x_2,\cdots} を決めれば良い

＊これが難しい

\textcolor{#78C2AD}{x_1,x_2,\cdots} の決め方

確率密度 \pi に収束させたい場合，強度 m^{(i)}(t)=\biggr(-v\cdot\nabla\log\pi(\textcolor{#78C2AD}{x_{i-1}}+tv)\biggl)_+,\quad t\ge0, を持つ非一様 Poisson 点過程をシミュレートする．

最初の到着点を \textcolor{#78C2AD}{x_i}=\textcolor{#78C2AD}{x_{i-1}}+vT_1^{(i)} とする．

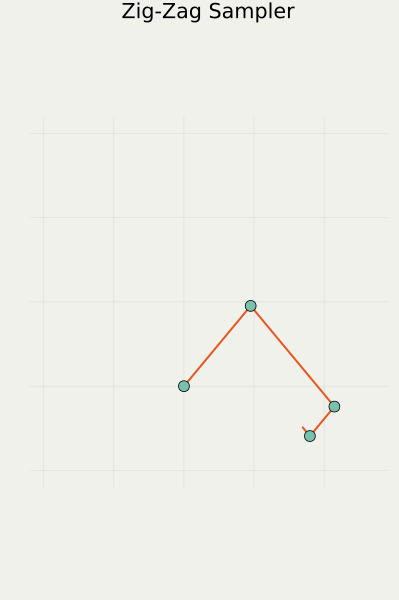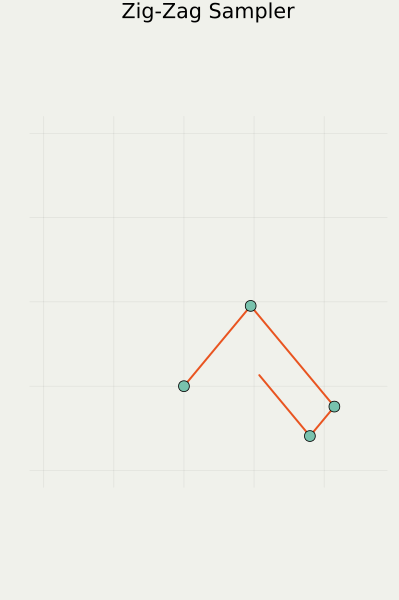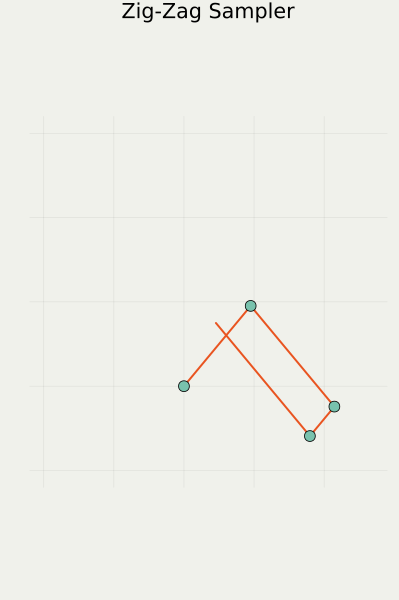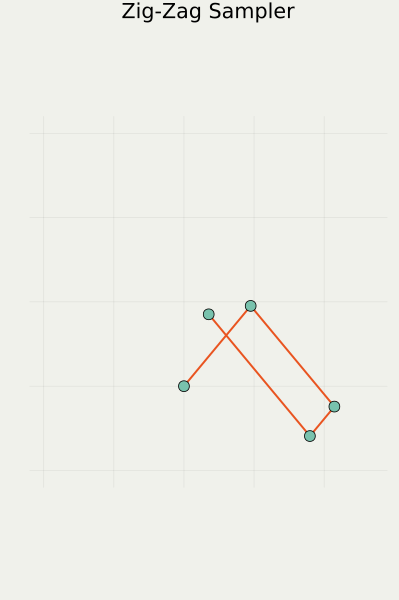
2.2 直観：１次元の場合

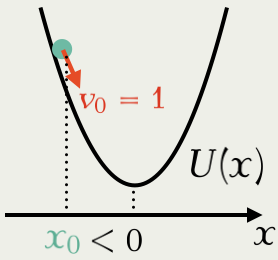
１次元の Gauss 分布を考える：

\pi(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{x^2}{2\sigma^2}} \therefore\quad U(x):=-\log\pi(x)=\frac{x^2}{2\sigma^2}+\mathrm{const.}

負の対数尤度 U=-\log\pi は ポテンシャル ともいう．

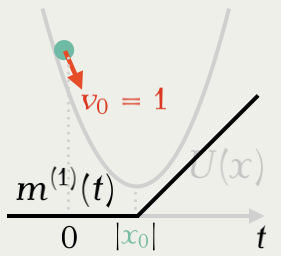
\begin{align*} m^{(1)}(t)&=(v_0\cdot U'(\textcolor{#78C2AD}{x_0}+\textcolor{#E95420}{v_0}t))_+\\ &=(\textcolor{#78C2AD}{x_0}+\textcolor{#E95420}{v_0}t)\cdot1{\left\{\textcolor{#78C2AD}{x_0}+\textcolor{#E95420}{v_0}t>0\right\}},\quad t\ge0, \end{align*} を強度にもつ 非一様 Poisson 点過程 の最初の到着時刻 T_1^{(1)} について，\textcolor{#78C2AD}{x_1}=\textcolor{#78C2AD}{x_0}+\textcolor{#E95420}{v_0}T_1^{(1)} とすれば良い．

2.3 課題：非一様 Poisson 点過程の到着時刻の計算

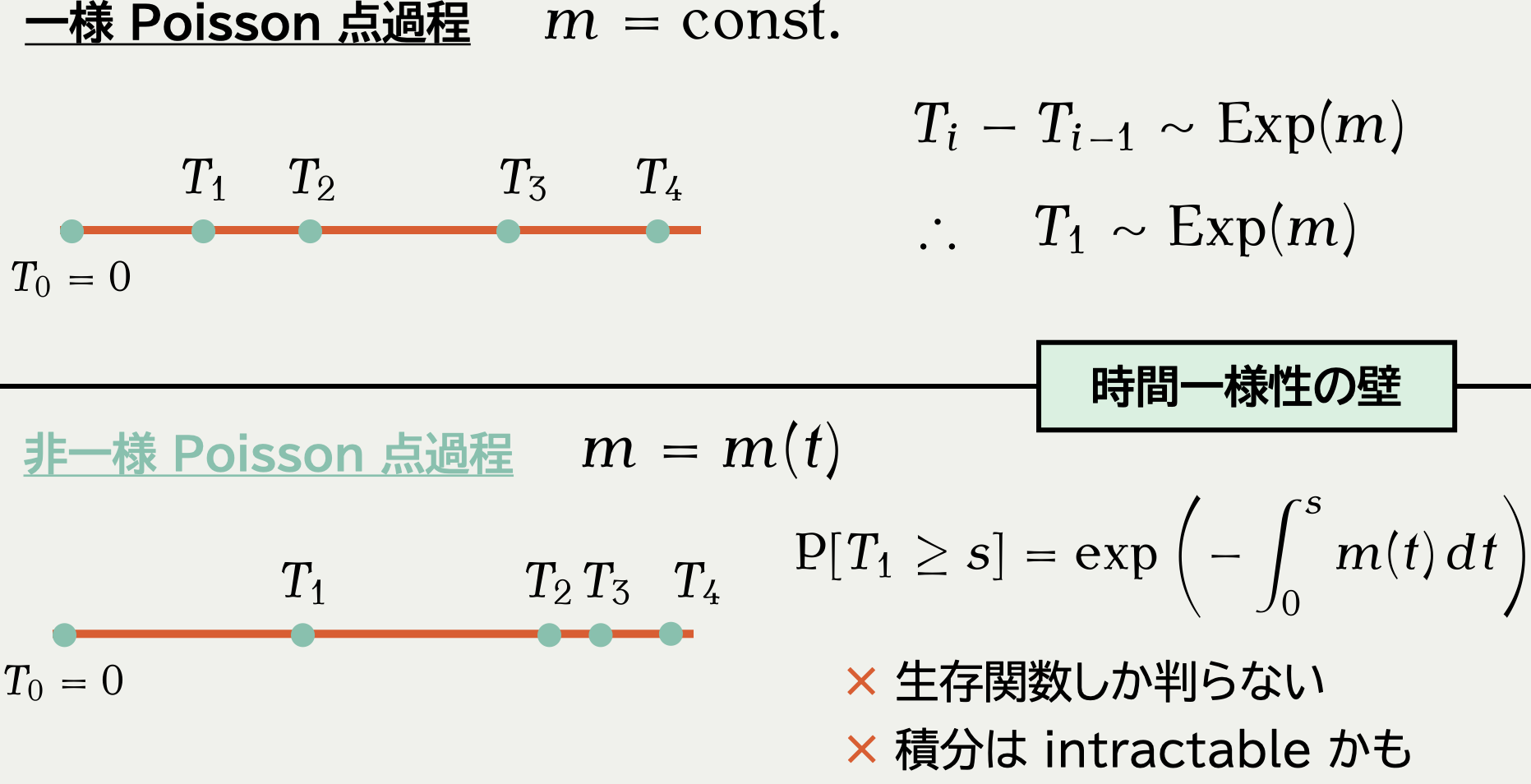
2.4 解決法：剪定 (Lewis and Shedler, 1979)

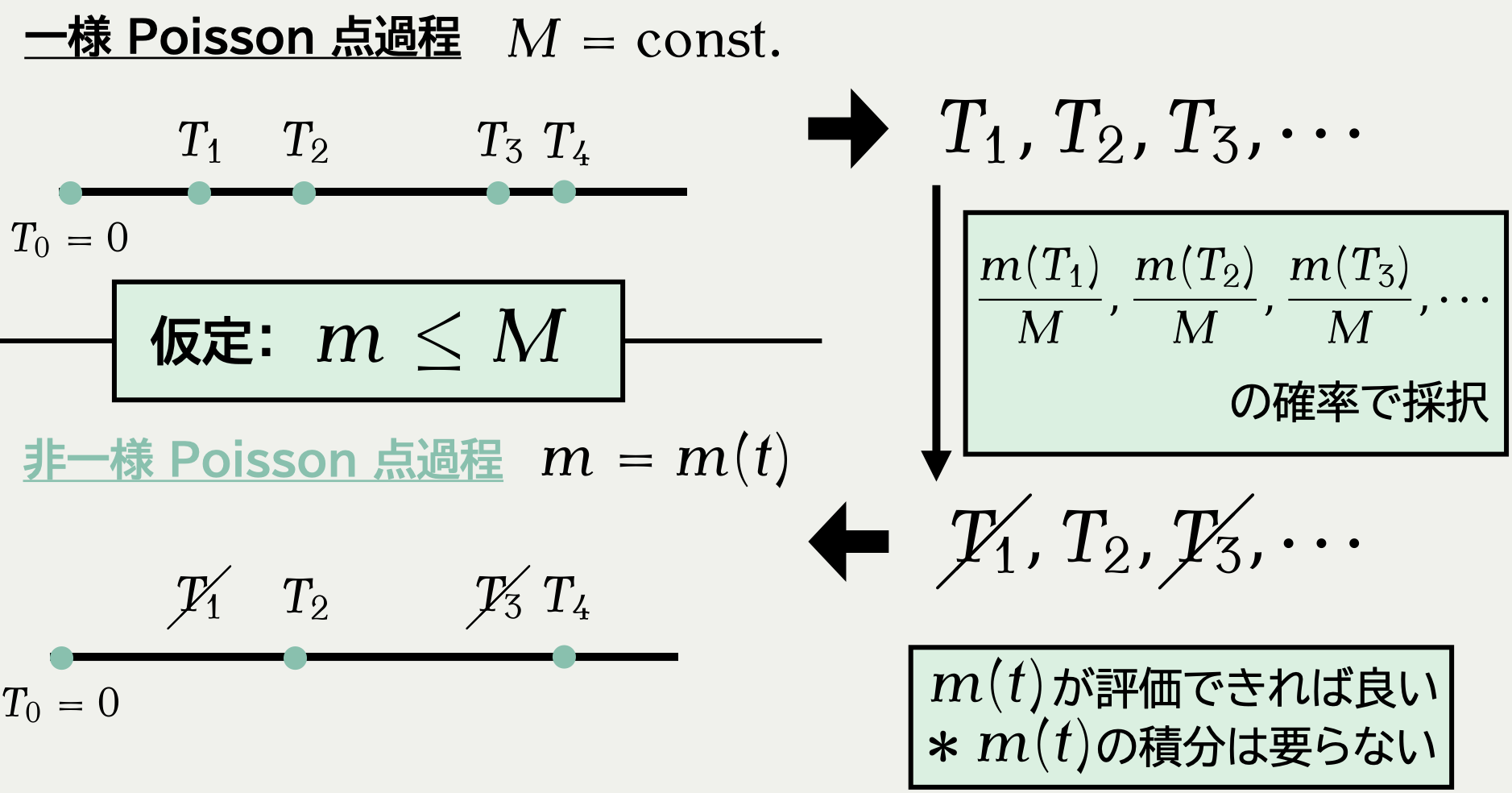
2.5 拡張：確率的剪定 (Sen et al., 2020)

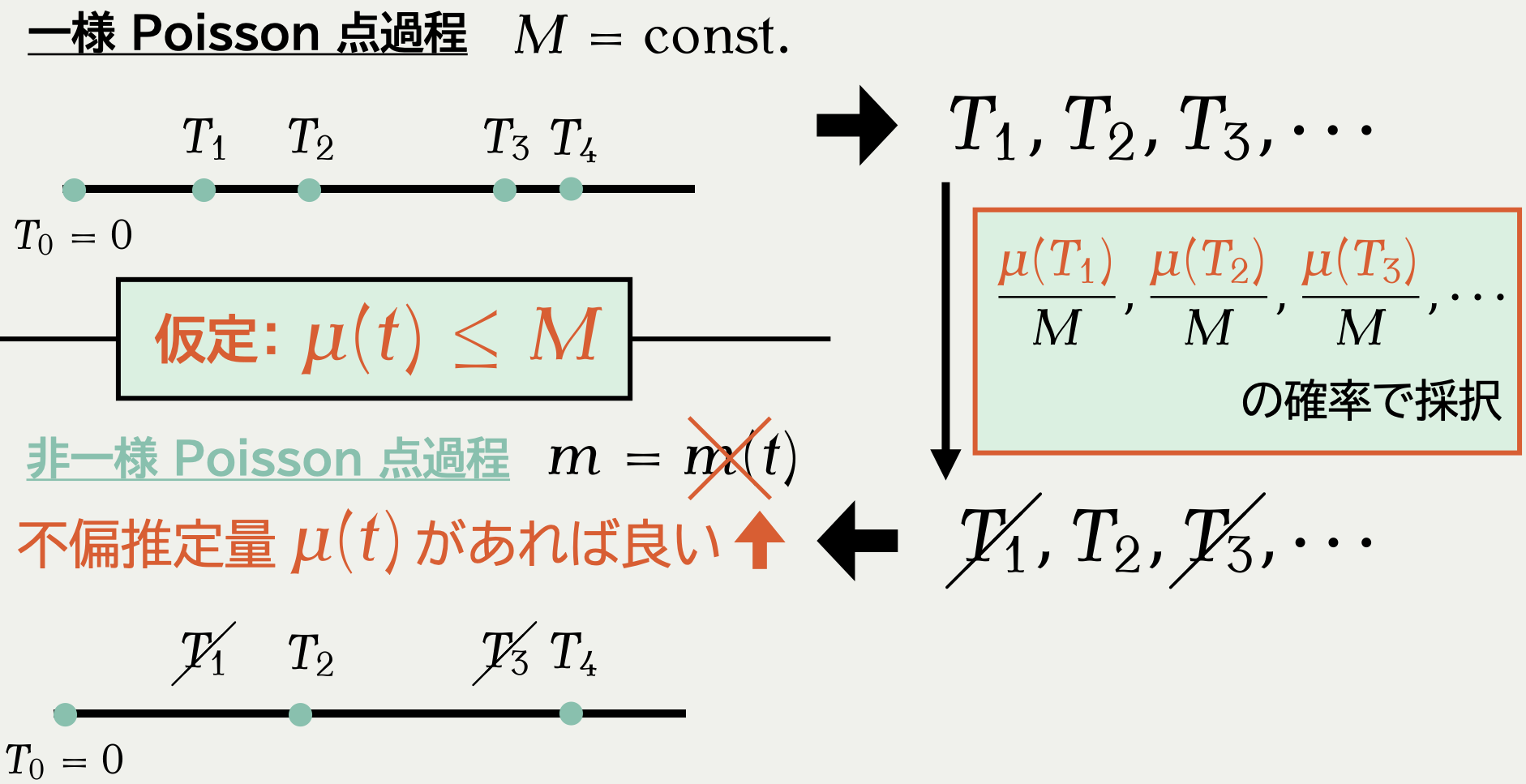
2.6 PDMP の美点：スケーラビリティが達成可能

m(t)=\biggr(-v\cdot\nabla\log\pi(\textcolor{#78C2AD}{x_{i-1}}+tv)\biggl)_+,\quad t\ge0, を強度に持つ非一様 Poisson 点過程をシミュレートする．

○ スケーラビリティが達成可能

m(t),\pi の評価：全データが必要

○ m(t) の不偏推定量 \mu(t)

　 データの一部を見るだけで計算可能

　○ 収束先が変わらない

既存研究：確率的剪定 (Bierkens et al., 2019), (Sen et al., 2020)

2.7 新課題：汎用的な上界 M の見つけ方が存在しない

m(t)=\biggr(-v\cdot\nabla\log\pi(\textcolor{#78C2AD}{x_{i-1}}+tv)\biggl)_+,\quad t\ge0, を強度に持つ非一様 Poisson 点過程をシミュレートする．

○ スケーラビリティが達成可能

m(t),\pi の評価：全データが必要

○ m(t) の不偏推定量 \mu(t)

　 データの一部を見るだけで計算可能

　○ 収束先が変わらない

既存研究：確率的剪定 (Bierkens et al., 2019), (Sen et al., 2020)

汎用的なアルゴリズムが存在しない

\mu(t)\le M\;\;\text{a.s.} を達成する上界 M をどう見つければ良いのか？

　 もっぱらロジスティック回帰くらい
　　　にしか使えなかった

今回の貢献：適応的剪定
(Andral and Kamatani, 2024)

3 新パッケージの実装

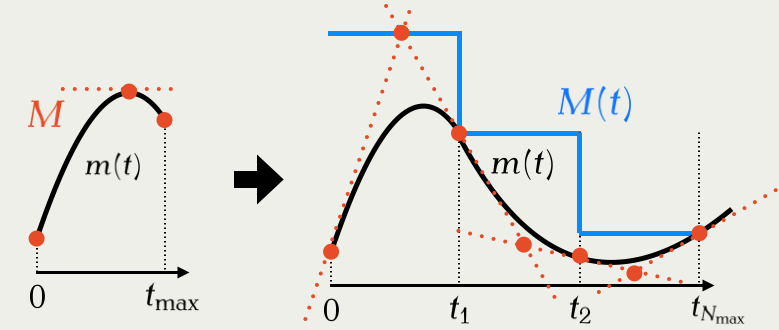
3.1 適応的剪定（従来法）(Corbella et al., 2022)

アルゴリズム
  1. \nabla\log\pi は 自動微分 で計算
  2. ホライゾン t_{\text{max}} を決めて M:=\max\{\textcolor{#E95420}{\text{３つの赤点}}\}
  3. \|M-m(t)\|_\infty が大き過ぎたら t_{\text{max}} を縮める

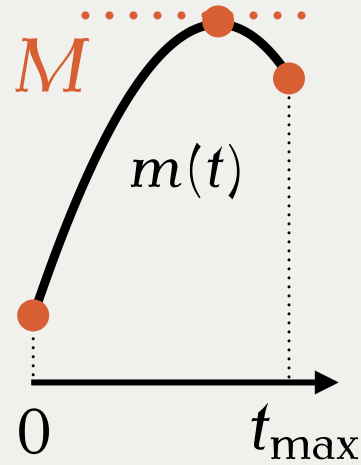
\displaystyle\max_{t\in[0,t_{\text{max}}]}m(t) の計算に最適化が必要

t_{\text{max}} の調整アルゴリズム？

3.2 新パッケージの実装 (Andral and Kamatani, 2024)

アルゴリズム
  1. \nabla\log\pi とグリッド点上での接線は 自動微分 で計算
  2. グリッド数 N_{\text{max}} を決めて，\textcolor{#0096FF}{M(t)} を構成．
  3. \textcolor{#0096FF}{M(t)}<m(t) が起こったらグリッド数 N_{\text{max}} を増やす．

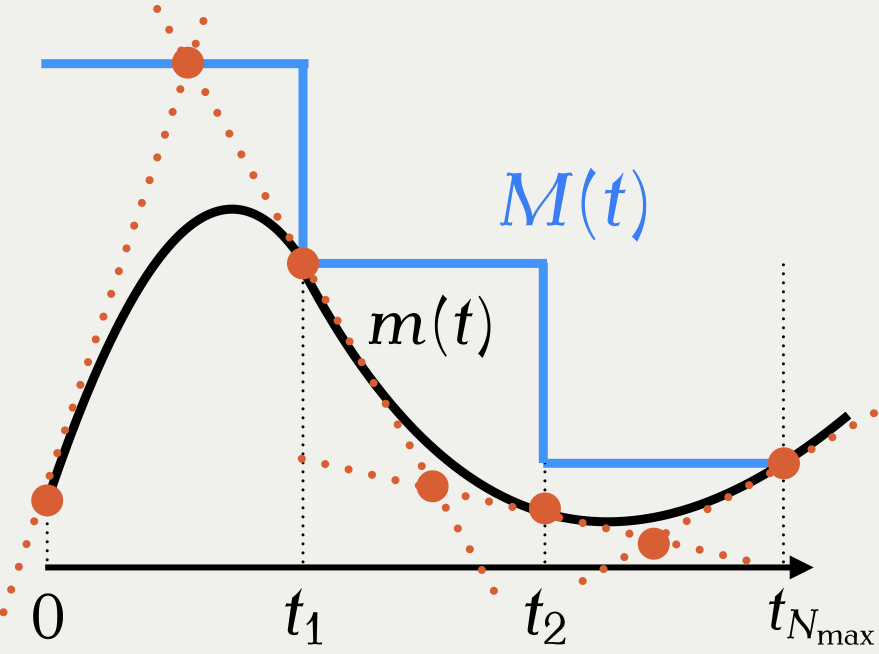
○ 最適化フリー＋自動微分のベクトライズで高速化可能

○ 自動的かつ汎用的なアルゴリズム

まとめ

① PDMP は新たなモンテカルロ法の枠組み

　もう武器は MCMC だけじゃない．

② PDMP でしか出来ないことも多い

　* バイアスを導入しないサブサンプリング

　* \delta_x 部分を持った非絶対連続分布からのサンプリング

③ 以上の「良さ」を保ったまま，汎用パッケージ化できる

2025年，機械学習・統計でも動き出す……？

非絶対連続分布からのサンプリングも可能 (Bierkens et al., 2023)

参考文献

Andral, C., and Kamatani, K. (2024). Automated techniques for efficient sampling of piecewise-deterministic markov processes.
Andrieu, C., and Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: Beyond the reversible scenario. The Annals of Statistics, 49(4), 1958–1981.
Bierkens, J., Fearnhead, P., and Roberts, G. (2019). The Zig-Zag Process and Super-Efficient Sampling for Bayesian Analysis of Big Data. The Annals of Statistics, 47(3), 1288–1320.
Bierkens, J., Grazzi, S., Kamatani, K., and Roberts, G. O. (2020). The boomerang sampler. Proceedings of the 37th International Conference on Machine Learning, 119, 908–918.
Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.
Bouchard-Côté, A., Vollmer, S. J., and Doucet, A. (2018). The bouncy particle sampler: A nonreversible rejection-free markov chain monte carlo method. Journal of the American Statistical Association, 113(522), 855–867.
Corbella, A., Spencer, S. E. F., and Roberts, G. O. (2022). Automatic Zig-Zag Sampling in Practice. Statistics and Computing, 32(6), 107.
Diaconis, P. (2013). Some things we’ve learned (about Markov chain Monte Carlo). Bernoulli, 19(4), 1294–1305.
Lewis, P. A. W., and Shedler, G. S. (1979). Simulation of nonhomogeneous poisson processes by thinning. Naval Research Logistics Quarterly, 26(3), 403–413.
Michel, M., Durmus, A., and Sénécal, S. (2020). Forward event-chain monte carlo: Fast sampling by randomness control in irreversible markov chains. Journal of Computational and Graphical Statistics, 29(4), 689–702.
Sen, D., Sachs, M., Lu, J., and Dunson, D. B. (2020). Efficient posterior sampling for high-dimensional imbalanced logistic regression. Biometrika, 107(4), 1005–1012.
Vasdekis, G., and Roberts, G. O. (2023). Speed up Zig-Zag. The Annals of Applied Probability, 33(6A), 4693–4746.

HMC との関係

  • Metropolis-Hastings ステップでは，尤度の比が 1 ならば棄却されない．
  • そこで尤度の等高線をなぞることを考える．
  • 運動量をランダムにサンプリングすることでエルゴード性を担保する．

ただし尤度の等高線をなぞることは数値計算の問題になり難しいが，ハイパーパラメータをうまくチューニングすることでほとんど独立なサンプルを得ることができる．

従来的には MCMC の１つとみれるが，ダイナミクスを複雑にした PDMP と見るべきかもしれない．

  • 尤度の等高線をなぞるダイナミクス
    • → 尤度の幾何情報を自然に取り入れた動きが可能
  • 運動量をリフレッシュするタイミングについての示唆？