動き出す PDMP

PDMPFlux.jl のアニメーションで見る MCMC の最近の発展

PDMP
MCMC
Process
Author

司馬博文

Published

12/24/2025

1 はじめに

PDMP (Piecewise Deterministic Markov Process) とは近年さかんに研究されている全く新しい MCMC の総称である．

収束が速い，大規模データに特に強い，密度が非正則だったりアトムを持っていても良いなど，理論的な期待は大きいが，その動いている様子を見たことのある者は，まだまだ一部の研究者に限られる．

HMC が Stan や PyMC に高度な実装があり，日々の統計と機械学習の実践を支えているのとは対照的である．

ここでは筆者が開発している Julia パッケージ PDMPFlux.jl を紹介する．

その最大の特徴は柔軟なアニメーション機能を提供する関数 anim_traj である．これにより種々の PDMP サンプラーの動きをアニメーションで見ることができる．本稿ではこの関数をフルに活用して，PDMP を「図解」してみたい．

PDMP はシミュレーション方法も未だ定まっておらず，実用上も理論上もまだまだ発展途上である．実は本パッケージは (Andral and Kamatani, 2024) の実装という点が特徴であるが，PDMP のアルゴリズムの側面には深入りしすぎず，本稿の終わりには PDMP の理論的な側面を少し紹介したい．

突然だが，クイズである．次クイズに答えるつもりで本稿を読んでみてほしい．

以下に，本パッケージが提供する PDMP サンプラー６つのうち３つを示す．このうち，最も高次元空間に強い手法はどれだろうか？

(Bouchard-Côté et al., 2018)

(Bierkens et al., 2019)

(Michel et al., 2020)
  • ただし，簡単のため，目標分布は標準 Gauss 分布 \(N_d(0,I_d)\) とする： \[ \pi^d(x)\,\propto\,e^{-U^d(x)},\qquad U^d(x)=\frac{\|x\|^2}{2}. \]
  • 「高次元に強い」とは，次のように決めるものとする：
    • 計算複雑性（例えば１つの独立サンプルを出力するのに要する \(U(x),\nabla U(x)\) 評価の回数）のスケール \(O(d^{\alpha})\) の \(\alpha\) が小さいと「強い」とする．
    • 同じスケールにおいては，同一回数の \(U(x),\nabla U(x)\) 評価（近似的に CPU 時間と比例するものとする）1で，より多くの独立サンプルを生み出す方が「強い」とする．

正解は本記事の最後に触れる．

それまでは，上の４つの gif が表す確率過程が，どのように生成されているか解説する．

PDMPFlux.jl の実装について詳しくなってもらうと同時に，６つの PDMP 手法を通じて，「より速い手法を作るにはどういうアイデアがあり得るか？」を一緒に考えて欲しい．実際，マジのアイデア不足である．

最後に，現状での理論が与える示唆を少し紹介する．

2 PDMP の基本：Poisson 点過程を打つ

基本的に，全ての PDMP アルゴリズムは点を打っている（＝特定の Poisson 点過程をシミュレーションしている）だけである．この時点で，既存の MCMC アルゴリズムとは全く違う．2

PDMP アルゴリズム＝緑の点がどこに来るかをシミュレーションする．緑の点で「どのように方向転換をするか」は，手法ごとに違う．

打った点の間を直線で（または他の規定の規則で）補間するだけで最終的な output が完成する（次のコードの sample_from_skeleton の部分）．

PDMPFlux.jl/src/sample.jl
function sample(
    sampler::AbstractPDMP,  # PDMP サンプラーの種類を指定
    N_sk::Int,  # シミュレーションするイベントの数
    N_samples::Int,  # 最終的に出力するサンプルの数
    xinit::Vector{Float64},  # 初期値（位置）
    vinit::Vector{Float64};  # 初期値（速度）
    seed::Int=nothing,  # 乱数のシード（必要ならば）
    verbose::Bool = true  # 進捗バーを表示するかどうか
)::Matrix{Float64}

    history = sample_skeleton(sampler, N_sk, xinit, vinit, seed=seed, verbose=verbose)
    return sample_from_skeleton(sampler, N_samples, history)

end

この sample_skeleton が PDMP シミュレーションの本質であり，中では「次のイベント時刻の特定」の繰り返しである．

仮に１つ前のイベント時刻 \(T_{i-1}\) で \((X_{T_{i-1}},V_{T_{i-1}})=(x,v)\in\mathbb{R}^{2d}\) まで来ているとしよう．すると，次のイベント時刻 \(T_i\) が来るまでの時間 \(T_i-T_{i-1}\) は，強度関数 \[ \lambda(t)=\max(0,\langle V_t|\nabla U(X_t)\rangle) \tag{1}\] で定まる．

強度関数 (intensity function) とは Poisson 点過程の双対可予測射影を指す語であるが，生存解析におけるハザード関数と捉えても良い．

結局，次のイベント時刻 \(T_i\) は \[ \operatorname{P}[T_i-T_{i-1}\ge t|T_{i-1}]=\exp\left(-\int^t_0\lambda(s)\,ds\right) \] に従って定まる．

\(\lambda\) が定数ならば，到着時間 \(T_i-T_{i-1}\) は指数分布である．しかし，式 (1) は「速度 \(V_t\) の，確率密度が下がっていく方向 \(\nabla U(X_t)\) の成分が大きければ大きいほどイベントが起きやすい」ことを意味する．

これにより，式 (1) に従ってイベント時刻を決定し，そこでうまく高密度領域に戻るような「方向転換」をデザインすれば，サンプラーを \(U(x)\) の値が大きい領域に誘導することができる．

これが，確率分布 \(\pi(x)\propto e^{-U(x)}\) に収束する PDMP の作り方である．

“PDMP” という名前についてであるが，直線部分が “piecewise deterministic” と呼ばれるゆえんであり，“Markov process” の部分は主に，方向転換が Markov 点過程に従うことと，方向転換の仕方がランダムである（場合がある）ことを指す．

3 PDMP サンプラー戦国時代：方向転換のデザイン

最も代表的な手法は BPS (Bouncy Particle Sampler) 群である．

これは Snell の反射の法則の通りに方向転換をする．つまり，イベントが起こった場合，ポテンシャル \(U(x)=-\log\pi(x)\) の等高線の接線を鏡に見立てて，反射する．式で表すと： \[ V_t^{\text{new}}\gets V_t-2\frac{\langle V_t|\nabla U(X_t)\rangle}{\|\nabla U(X_t)\|^2}\nabla U(X_t). \]

これにより速度 \(V_t\) のうち \(\nabla U(X_t)\) に平行だった成分は反射され，垂直な成分はそのまま残る．

(Bouchard-Côté et al., 2018)

(Bierkens et al., 2020)

右側の Boomerang Sampler では参照測度が違う．BPS と同じメカニズムだが，\(\mathbb{R}^n\) 上の Lebesgue 測度に対して設計する代わりに，標準 Gauss 測度に対して設計されている．このため，\(\mathbb{R}^{\infty}\) 上でも定義可能な手法になっている．3 このような手法は function space MCMC とも呼ばれる (Cotter et al., 2013)．

この BPS 群の最大の欠点は refreshment という追加の動作が必要な点である．定期的に速度 \(V_t\) を平衡分布にリセットする必要がある．

さもなくば，ダイナミクスのランダムネスが不足し，エルゴード性が失われたり，すごく遅くなったりする：

Code 
using PDMPFlux, Plots

@inline function ∇U(x::AbstractVector)
  return x
end

dim = 2
sampler = BPS(dim, ∇U; refresh_rate=0.0)

N_sk, xinit, vinit = 1_000, randn(dim), randn(dim)
vinit = vinit ./ sqrt(sum(vinit.^2))

output_BPS = sample_skeleton(sampler, N_sk, xinit, vinit, seed=20250428)
x_BPS = output_BPS.X
v_BPS = output_BPS.V
t_BPS = output_BPS.t

anim_traj(output_BPS, 100; plot_start=50, filename="BPS.gif", color="#E95420", scatter_color="#78C2AD", background="#F0F1EB", title="BPS without Refreshment", xlabel="", ylabel="", axis=false)

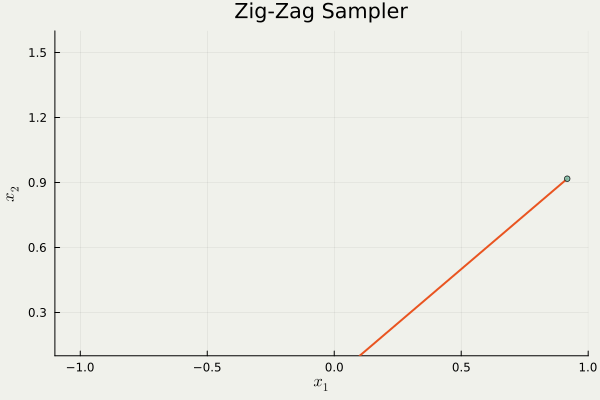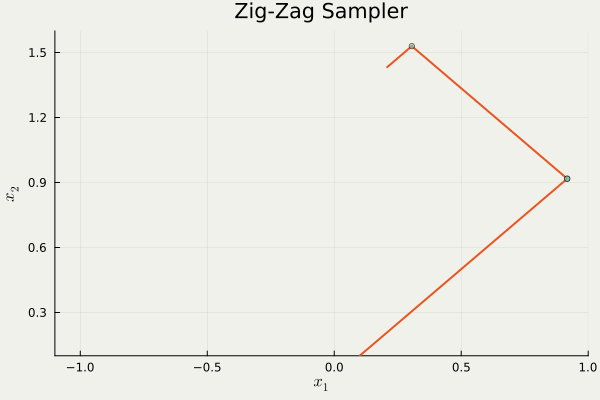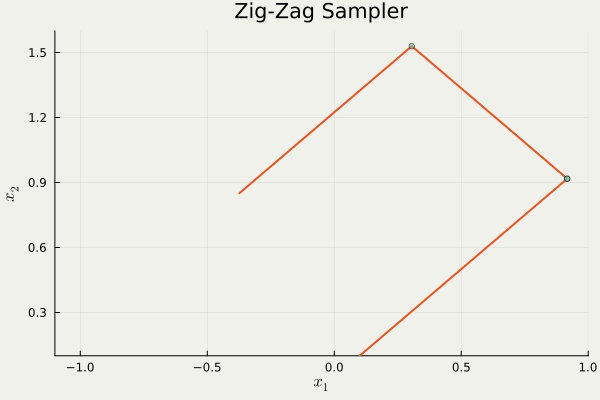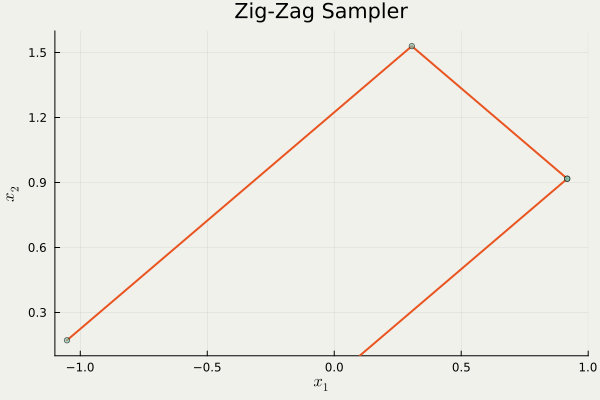
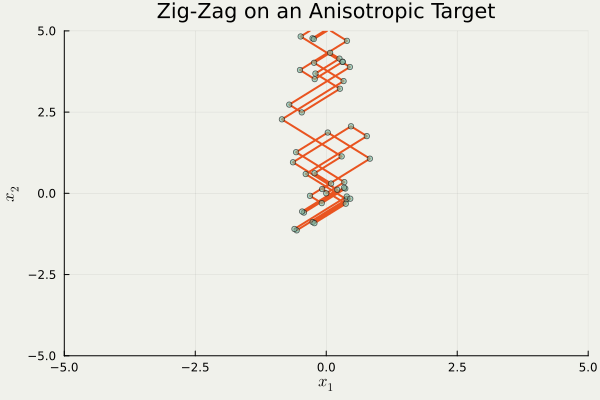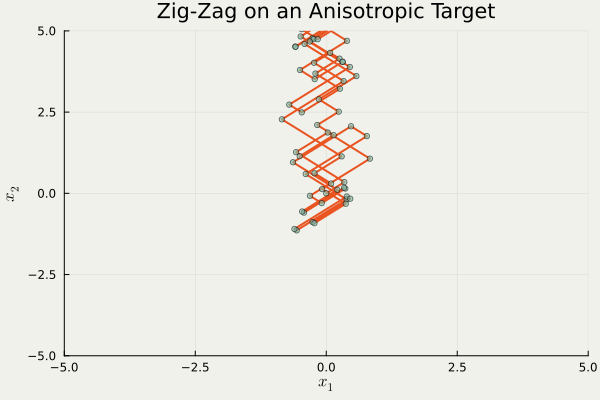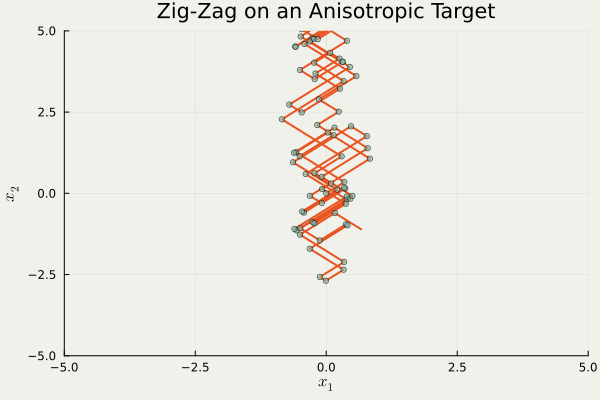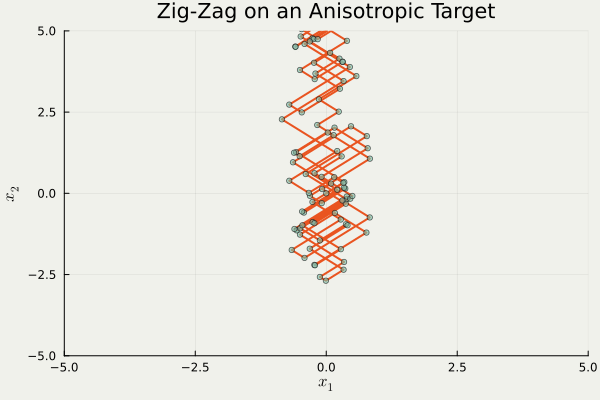
この問題を迂回する１つの方法は，そもそも進行方向を \(\{\pm1\}^d\) に制限することである．

(Bierkens et al., 2019)

これは trajectory の形状から Zig-Zag sampler と呼ばれるが，異方性に弱いという欠点がある．

つまり，分布の形状が \(\{\pm1\}^d\) にうまく沿っていない場合，大変非効率的な移動を強いられるという欠点がある．

Code 
using PDMPFlux, LinearAlgebra

const γ = 10

@inline function ∇U(x::AbstractVector)
  return [γ,1/γ] ⋅ x
end

dim = 2
sampler = ZigZag(dim, ∇U; refresh_rate=0.0)

N_sk, xinit, vinit = 1_000, zeros(dim), ones(dim)

output_ZZ = sample_skeleton(sampler, N_sk, xinit, vinit, seed=20250428)
x_ZZ = output_ZZ.X
v_ZZ = output_ZZ.V
t_ZZ = output_ZZ.t

anim_traj(output_ZZ, 100; plot_start=50, filename="ZZS.gif", color="#E95420", scatter_color="#78C2AD", background="#F0F1EB", title="Zig-Zag on an Anisotropic Target", xlims=(-5, 5), ylims=(-5, 5))

4 PDMP の最近の発展

以上，今まで見てきたどの手法も得手・不得手というものがあった．

4.1 FECMC：確率的反射，部分的リフレッシュ

今までの手法は全て，方向転換の仕方がシンプルで，ランダムネスは（実は）ない．

Forward Event-Chain Monte Carlo 法 (Michel et al., 2020) は，「ランダムな反射」を設計することで，「リフレッシュ動作が欠かせない」という先述の BPS の欠点を克服した．

特に「絶対に今来た道を戻らない “Forward”」という設計が凝らされており，次のようにくるくる回る軌道を描く：

(Michel et al., 2020)

名前についてであるが，ECMC (Event-Chain Monte Carlo) 法とは，実は PDMP という名前がついて統計に輸入される前の，物理学で用いられていた手法である (Bernard et al., 2009), (Michel et al., 2014), (Nishikawa et al., 2015), (Krauth, 2021)．

そもそも PDMP とは ECMC などの名前で，はじめて氷の融解の過程の全原子シミュレーションに成功（！）して (Bernard and Krauth, 2011)，満を持して統計分野に輸入されたのであった．4

4.2 Sticky PDMP：アトムを含む分布への解決策

PDMP はなんといっても連続時間の軌道を出力するという点に，過去の Monte Carlo 法にない特徴がある．

この特徴が極めて不思議な応用をもたらしてくれることを，コミュニティは近年自覚しつつある．

まず，目標の確率分布は絶対連続じゃなく，アトムが有限個含まれていても良い．

例えば，変数選択のことを考えて，事後分布が \(\alpha\pi(x)+(1-\alpha)\delta_0(dx)\) という形で表せたとしよう．

この \(\alpha\) の値（回帰で言えば，当該変数の事後包含確率）の値と，モデルに含まれた場合の事後分布を同時にサンプリングしたい場合，Sticky Zig-Zag sampler (Bierkens et al., 2023) が使える：

(Bierkens et al., 2023)

4.3 Speed-Up PDMP：加速による重点サンプリング

連続時間のアルゴリズムになったため，「加速」という概念が生まれる．

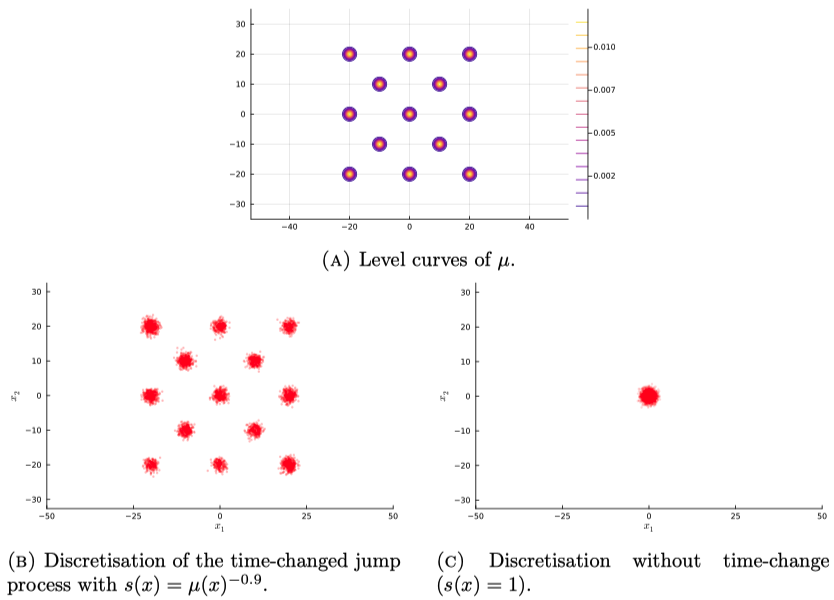
単に加速するのではなく，位置に応じてサンプラーの速さを変えることで，分布の「どこを重視して欲しいか」を指定する使い方ができる．

これにより，裾が重い分布における尾部領域や，多峰性分布における谷の部分など，従来の MCMC では探索が困難であった領域に，違った重みを与えることができる．

(Vasdekis and Roberts, 2023)

(Bertazzi and Vasdekis, 2025) では，なんと 13 成分の混合 Gauss 分布から，ひとつもモードを潰さない正確なサンプリングを達成していることを報告している：

(Bertazzi and Vasdekis, 2025, p. 19 Figure 4)

5 クイズの答え

正解は Forward Event-Chain Monte Carlo である．

(Michel et al., 2020)

ただし，ほとんどのサンプラーには，ターゲット分布が factorized な形 \(\pi(x)=\prod_{f\in F}\pi_f(x_f)\) で書ける場合にだけ使える効率的な実装法があり，これを採用した場合のスケーリングは HMC も凌ぐ (Krauth, 2024)．

実はこの局所性を活かした実装が，ECMC という名前で，氷などの凝縮系の Monte Carlo シミュレーションで圧倒的な性能を見せつけてきた理由である．この点は (Tartero and Krauth, 2024) などが良い入門になる．

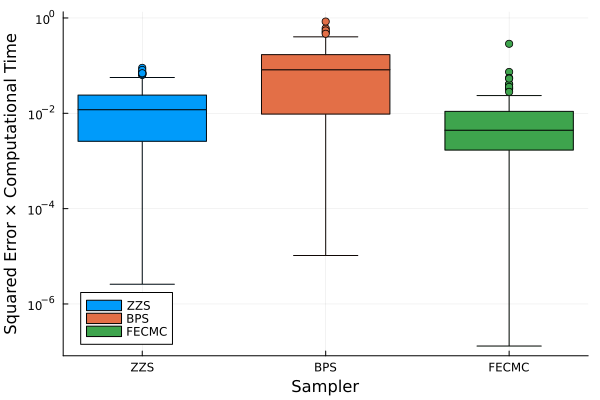
ここでは BPS, Zig-Zag, FECMC の，一般のターゲット分布に対して通用する実装で比較してみる（PDMPFlux.jl のデフォルト実装）．

例えば，テスト関数 \(h(x)=\|x\|^2\) の期待値を推定する際の二乗誤差を比較してみると，FECMC の方が効率が良さがわかる：

Code 
using PDMPFlux, Plots, ProgressBars, LinearAlgebra, StatsPlots

const dim = 100

@inline function ∇U(x::AbstractVector)
  return x
end

@inline function ∇U_Boomerang(x::AbstractVector)
  return ones(dim)
end

function h_estimate_online(
  sampler::PDMPFlux.AbstractPDMP,
  T_end::Float64,
  xinit::Vector{Float64},
  vinit::Vector{Float64};
  seed::Union{Int, Nothing}=nothing,
)::Float64
  if !(isfinite(T_end)) || T_end < 0
    throw(ArgumentError("T_end must be finite and non-negative. Current value: $T_end"))
  end
  d = length(xinit)
  if d == 0
    throw(ArgumentError("xinit must be non-empty"))
  end
  if T_end == 0.0
    return 0.0
  end

  state = PDMPFlux.init_state(sampler, xinit, vinit, seed)

  estimate = 0.0

  # 現在のイベント点（post-jump）を保持し、次イベントまでの区間寄与を足す
  t_prev = state.t
  x_prev = copy(state.x)
  v_prev = copy(state.v)

  while t_prev < T_end
    PDMPFlux.get_event_state!(state, sampler)  # mutates state in-place; advances state.t to next accepted event
    t_next = state.t

    if t_next <= T_end
      Δt = t_next - t_prev
      # 区間 [t_prev, t_next] は (x_prev, v_prev) からの flow
      nx = dot(x_prev, x_prev)
      xv = dot(x_prev, v_prev)
      estimate += nx * Δt + (Δt^3) / 3 + (Δt^2) * xv

      t_prev = t_next
      copyto!(x_prev, state.x)
      copyto!(v_prev, state.v)
    else
      # overshoot: 最後は flow で t=T_end の点を作ってそこで打ち切る
      Δt = T_end - t_prev
      nx = dot(x_prev, x_prev)
      xv = dot(x_prev, v_prev)
      estimate += nx * Δt + (Δt^3) / 3 + (Δt^2) * xv
      break
    end
  end

  return (estimate - d * T_end) / sqrt(d) / T_end  # CAUTION: inprecise denominator (intentionally)
end

function Experiment_once()
  ZZS = ZigZag(dim, ∇U; refresh_rate=0.0)
  T, xinit, vinit = Float64(1000), randn(dim), ones(dim)
  t_ZZ = @elapsed output_ZZ = h_estimate_online(ZZS, T, xinit, vinit)

  BPS_sampler = BPS(dim, ∇U; refresh_rate=1.4)
  vinit = randn(dim)
  vinit = vinit ./ norm(vinit)
  t_BPS = @elapsed output_BPS = h_estimate_online(BPS_sampler, T, xinit, vinit)

  vinit = randn(dim)
  vinit = vinit ./ norm(vinit)
  FECMC = ForwardECMC(dim, ∇U)
  t_ForwardECMC = @elapsed output_ForwardECMC = h_estimate_online(FECMC, T, xinit, vinit)
  return [abs2(output_ZZ) * t_ZZ, abs2(output_BPS) * t_BPS, abs2(output_ForwardECMC) * t_ForwardECMC]
end

function Experiment(iter::Int=100)
  results = Matrix{Float64}(undef, iter, 3)
  for i in ProgressBar(1:iter)
    results[i,:] = Experiment_once()
  end
  return results
end

results = Experiment(100)

iter  = size(results, 1)
labels = ["ZZS", "BPS", "FECMC"]
groups = repeat(labels, inner=iter)
groups = categorical(groups; ordered=true, levels=labels)
boxplot(groups, vec(results);
    group = groups,
    bar_width = 0.7,
    legend = :bottomleft,
    xlabel = "Sampler",
    ylabel = "Squared Error × Computational Time",
    yscale = :log10)

縦軸は実行時間によって調節した平均自乗誤差 (MSE) であり，小さいほど性能が良い．

この性能差はスケーリング極限／拡散近似の数学によって理論的に説明することができる．

6 参考文献

Andral, C., and Kamatani, K. (2024). Automated techniques for efficient sampling of piecewise-deterministic markov processes.
Bernard, E. P., and Krauth, W. (2011). Two-step melting in two dimensions: First-order liquid-hexatic transition. Phys. Rev. Lett., 107, 155704.
Bernard, E. P., Krauth, W., and Wilson, D. B. (2009). Event-chain monte carlo algorithms for hard-sphere systems. Phys. Rev. E, 80, 056704.
Bertazzi, A., and Vasdekis, G. (2025). Sampling with time-changed markov processes.
Bierkens, J., Fearnhead, P., and Roberts, G. (2019). The Zig-Zag Process and Super-Efficient Sampling for Bayesian Analysis of Big Data. The Annals of Statistics, 47(3), 1288–1320.
Bierkens, J., Grazzi, S., Kamatani, K., and Roberts, G. O. (2020). The boomerang sampler. Proceedings of the 37th International Conference on Machine Learning, 119, 908–918.
Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.
Bouchard-Côté, A., Vollmer, S. J., and Doucet, A. (2018). The Bouncy Particle Sampler: A Nonreversible Rejection-Free Markov Chain Monte Carlo Method. Journal of the American Statistical Association, 113(522), 855–867.
Cotter, S. L., Roberts, G. O., Stuart, A. M., and White, D. (2013). MCMC Methods for Functions: Modifying Old Algorithms to Make Them Faster. Statistical Science, 28(3), 424–446.
Krauth, W. (2021). Event-chain monte carlo: Foundations, applications, and prospects. Frontiers in Physics, Volume 9 - 2021.
Krauth, W. (2024). Hamiltonian Monte Carlo vs. Event-Chain Monte Carlo: An Appraisal of Sampling Strategies beyond the Diffusive Regime.
Michel, M., Durmus, A., and Sénécal, S. (2020). Forward event-chain monte carlo: Fast sampling by randomness control in irreversible markov chains. Journal of Computational and Graphical Statistics, 29(4), 689–702.
Michel, M., Kapfer, S. C., and Krauth, W. (2014). Generalized event-chain monte carlo: Constructing rejection-free global-balance algorithms from infinitesimal steps. The Journal of Chemical Physics, 140(5), 054116.
Nishikawa, Y., Michel, M., Krauth, W., and Hukushima, K. (2015). Event-chain algorithm for the heisenberg model: Evidence for \(z\ensuremath{\simeq}1\) dynamic scaling. Phys. Rev. E, 92, 063306.
Peters, E. A. J. F., and de With, G. (2012). Rejection-free monte carlo sampling for general potentials. Physical Review E, 85(2).
Tartero, G., and Krauth, W. (2024). Concepts in Monte Carlo Sampling. American Journal of Physics, 92(1), 65–77.
Vasdekis, G., and Roberts, G. O. (2023). Speed up Zig-Zag. The Annals of Applied Probability, 33(6A), 4693–4746.

Footnotes

  1. シミュレーション法が定まっていないのでうまく言えないが，理想的なアルゴリズムではほとんどその通りになる．↩︎

  2. だが，最終的に最もうまくいく MCMC アルゴリズムと，最もうまくいく PDMP アルゴリズムは，確率過程としてはとても似通ってくる．シミュレーション方法が違うのみである．↩︎

  3. \(\mathbb{R}^{\infty}\) または一般の可分 Hilbert 空間上では Lebesgue 測度は存在しないが，Gauss 測度は存在し続ける．↩︎

  4. 他にも直接の祖先は ECMC 以外にも辿れる (Peters and de With, 2012)．↩︎