A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1 概観
1.1 BPS のポテンシャル
BPS のポテンシャルは OU 過程に収束する: \[ dY_t=-\theta(\rho)^2/4\cdot Y_t\,dt+\sigma(\rho)\,dB_t. \]
1.2 非有界な速度を持つ BPS のポテンシャル
\(\mu=\mathrm{U}(S^{d-1})\) とした場合と \(\mu=\operatorname{N}_d(0,I_d)\) とした場合とで,全く違う動きをする.
したがって,\(\mu=\operatorname{N}_d(0,I_d)\) と取った場合はまた違う過程に収束するものと思われる.
いや,同じか?
1.3 FECMC のポテンシャル
1.4 Zig-Zag のポテンシャル
2 BPS と FECMC の比較
2.1 ポテンシャルの挙動
2.2 動径運動量の挙動 (d=1000の場合)
2.3 有限次元周辺分布の挙動
次元数 \(d\) を少しずつ大きくしながら,最初の1または2成分のみをみていく.
2.3.1 BPS
BPS は速度成分の分布を変えることで,収束先が違う.
驚くべきことに,\(\mu=\operatorname{N}_d(0,I_d)\) と取ると,Boomerang sampler (Bierkens et al., 2020) の挙動に酷似していく.
これはポテンシャル \(U\) が定める Hamiltonian フローにトラップされていくためである.
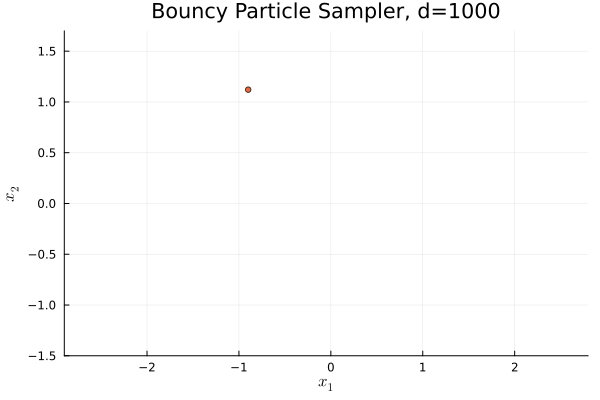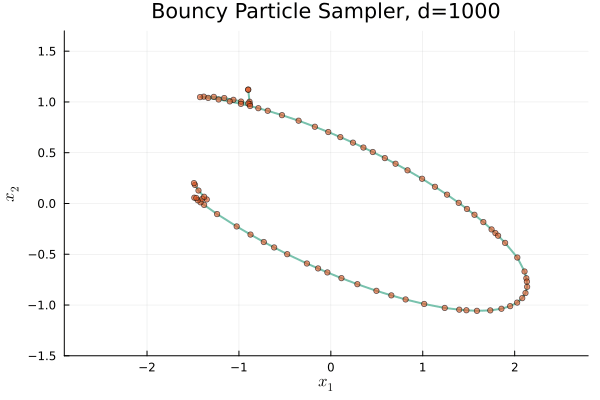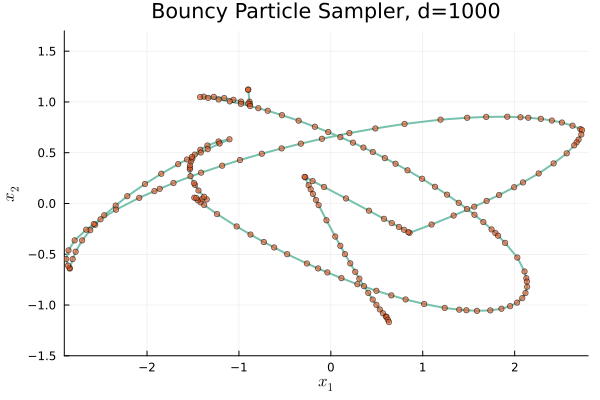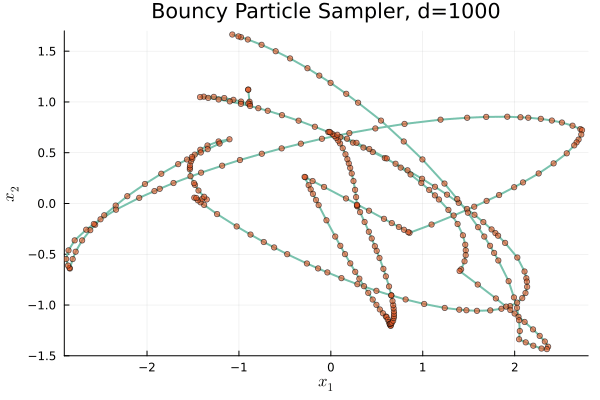
しかし \(\mu\) を \(S^{d-1}\subset\mathbb{R}^d\) 上の一様分布に取ると,次の通り,全く違った挙動になる:
2.3.2 FECMC
References
Bierkens, J., Grazzi, S., Kamatani, K., and Roberts, G. O. (2020). The boomerang sampler. Proceedings of the 37th International Conference on Machine Learning, 119, 908–918.