FECMC と BPS で見る hypocoercivity

PDMP
MCMC
Process
Author

Draft Draft

Published

11/20/2025

FECMC と BPS の高次元での性能差の鍵を握るのが，角運動量過程 (RMP: Radial Momentum Process) \[ R_t^{(d)}:=\langle X_t^{(d)}, V_t^{(d)}\rangle=\sum_{i=1}^dX_t^{(d),i}V_t^{(d),i} \] である．その積分で定まる過程が，原点からの距離に他ならないからである．

つまり，高次元での角運動量過程の mixing の速さが，高次元で FECMC と BPS が動径方向に mixing する速さとほとんど一致する．

本稿では数値実験を通じて，次のように FECMC が BPS を強く優越することを見る：

1 Autocorelation Decay of the FECMC Limit RMP

\[ Lf(x)=f'(x)+x_+\biggr(Rf(-x)-f(x)\biggl),\qquad f\in C^2_c(\mathbb{R}), \] \[ Rf(x):=\int^\infty_0f(y)\,r(y)\,dy,\qquad r(y)=ye^{-\frac{y^2}{2}}. \]

using Random, Distributions, Plots, LaTeXStrings

function SimulateSkeleton(x₀; T::Float64=20.0, seed::Int=0)
  if seed == 0
    τ = () -> rand(Rayleigh(1.0))
  else
    rng = MersenneTwister(seed)
    τ = () -> rand(rng, Rayleigh(1.0))
  end

  if x₀ <= 0
    tₑ = -x₀ + τ()
  else
    if seed == 0
      tₑ = -x₀ + sqrt(x₀^2 - 2log(1-rand()))
    else
      tₑ = -x₀ + sqrt(x₀^2 - 2log(1-rand(rng)))
    end
  end

  skeletons = [0.0, tₑ]
  positions = [x₀]

  while tₑ < T
    τ₁, τ₂ = τ(), τ()
    tₑ += τ₁ + τ₂
    push!(skeletons, tₑ)
    push!(positions, -τ₁)
  end

  return skeletons[1:end-1], positions
end

function DiscretizeSkeleton(skeletons::Vector{Float64}, positions::Vector{Float64}; dt::Float64=0.005, T::Float64=10.0)

  tᵢ = 0.0:dt:T
  i = searchsortedfirst.(Ref(skeletons), tᵢ) .- 1
  i[1] = 1
  flow = (x,t) -> x + t
  locate = (j,t) -> flow(positions[j], t - skeletons[j])
  samples = [locate(j, t) for (j, t) in zip(i, tᵢ)]

  return tᵢ, samples
end

function sample(x₀::Float64; T::Float64=10.0, seed::Int=0, dt::Float64=0.005)

  skeletons, positions = SimulateSkeleton(x₀, seed=seed)
  tᵢ, samples = DiscretizeSkeleton(skeletons, positions, dt=dt, T=T)
end

plot(sample(randn(), T=20.0), xlabel=L"t", ylabel=L"R_t", label="FECMC Limit RMP") |> q -> hline!(q, [0], linewidth=0.8, color=:black, label="")
function calc_covariance(N::Int=10^5; seed::Int=0, x₀=nothing)
  t, x = sample(0.0, seed=seed)
  ρₙ = Matrix{Float64}(undef, N, length(t))

  if x₀ isa Nothing
    for i in 1:N
      x₀ = randn()
      t, x = sample(x₀, seed=seed)
      ρₙ[i, :] = x₀ * x
    end
  else
    for i in 1:N
      t, x = sample(x₀, seed=seed)
      ρₙ[i, :] = x  # This is no longer a covariance. Will be used for resolvent.
    end
  end

  return t, mean(ρₙ, dims=1)[:]
end

t, m = calc_covariance()

print(sum(m) * step(t))
p = plot(t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_tX_0]", label="FECMC", linewidth=3, size=(800, 400), left_margin=5Plots.mm, bottom_margin=3Plots.mm)
p
0.4073259178058479

この積分値は \(\sqrt{1/2\pi}\approx0.399\) が理論値であり，実際この値の周りで揺動している：

function calc_ρ0(N::Int=10)
  MCEstimates = Vector{Float64}(undef, N)
  for i in 1:10
    t, m = calc_covariance()
    MCEstimates[i] = sum(m) * step(t)
  end
  return mean(MCEstimates), std(MCEstimates)
end
m, σ = calc_ρ0()
print("Monte Carlo estimate: $(m) ± $(σ)")
Monte Carlo estimate: 0.3999923191443751 ± 0.009112396988848593

ブログに載せる際の計算量の問題で，Monte Carlo サンプルサイズ \(N\) を小さく抑えているため，ギザギザしている．\(N\) を十分大きくしたプロットは第 3 節で示す．

2 Autocorelation Decay of the BPS Limit RMP

The following result is also presented at the end of the Section 1 of (Bierkens et al., 2022).

function SimulateBPSSkeleton(x₀; T::Float64=20.0, seed::Int=0)

  if seed == 0
    τ = () -> rand(Rayleigh(1.0))
  else
    rng = MersenneTwister(seed)
    τ = () -> rand(rng, Rayleigh(1.0))
  end

  if x₀ <= 0
    tₑ = -x₀ + τ()
  else
    if seed == 0
      tₑ = -x₀ + sqrt(x₀^2 - 2log(1-rand()))
    else
      tₑ = -x₀ + sqrt(x₀^2 - 2log(1-rand(rng)))
    end
  end

  skeletons = [0.0, tₑ]
  positions = [x₀, - (x₀ + tₑ)]

  while tₑ < T
    τ₁ = τ()
    tₑ += -positions[end] + τ₁
    push!(skeletons, tₑ)
    push!(positions, -τ₁)
  end

  return skeletons[1:end-1], positions
end

function sampleBPS(x₀::Float64; seed::Int=0, T::Float64=10.0, dt::Float64=0.005)

  skeletons, positions = SimulateBPSSkeleton(x₀, seed=seed)
  tᵢ, samples = DiscretizeSkeleton(skeletons, positions, dt=dt, T=T)
end

plot(sampleBPS(randn(), T=20.0), xlabel=L"t", ylabel=L"R_t", label="BPS Limit RMP") |> q -> hline!(q, [0], linewidth=0.8, color=:black, label="")
function calc_BPS_Covariance(N::Int=10^5; seed::Int=0, x₀=nothing)
  t, x = sampleBPS(0.0, seed=seed)
  ρₙ = Matrix{Float64}(undef, N, length(t))

  if x₀ isa Nothing
    for i in 1:N
      x₀ = randn()
      t, x = sampleBPS(x₀, seed=seed)
      ρₙ[i, :] = x₀ * x
    end
  else
    for i in 1:N
      t, x = sampleBPS(x₀, seed=seed)
      ρₙ[i, :] = x  # This is no longer a covariance. Will be used for resolvent.
    end
  end

  return t, mean(ρₙ, dims=1)[:]
end

t, m = calc_BPS_Covariance()

print(sum(m) * step(t))

plot!(p, t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_tX_0]", label="BPS", linewidth=3, left_margin=5Plots.mm, bottom_margin=3Plots.mm)
0.008061565592538308

この理論値は \(0\) である．

FECMC の方が負方向への揺り戻しの際，反射ではなく幅を取り直しているので，負の相関の overshoot が抑えられている様子が見える．

3 Performance Comparison: Refreshed FECMC vs. BPS

\(N=10^6\) として計算したのが次のプロットである：

ここから，ポテンシャルの過程の拡散係数 \(\sigma(\rho)^2\) を見る．これは Laplace 変換の定数倍 \[ \sigma(\rho)^2:=8\int^\infty_0K(s,\rho)\,ds \] によって定義され，ほとんど角運動量過程 \(R_t\) の mixing の速さに一致する．

この値を見ることで，FECMC ではリフレッシュをすると性能が逆に悪くなることが綺麗に見て取れる！

Therefore, we pretty much reconstructed the figures of (Bierkens et al., 2022), adding an extra analysis of FECMC.

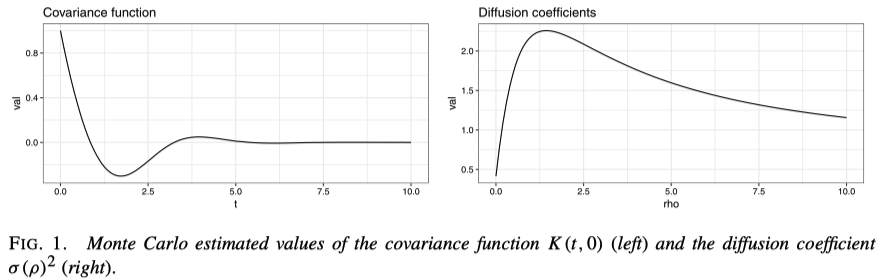
4 Resolvent

このときの Laplace 変換で定まる汎函数は，Resolvent と呼ばれる： \[ (\rho-G)^{-1}\mathrm{id}(x)=\int^\infty_0e^{-\rho t}\operatorname{E}_x[X_t]\,dt. \]

この値を \(x\in[-0.5,1.0]\) でプロットしてみる．

function calc_BPS_resolvent(ρ::Float64=1.0, iter::Int=10, T::Float64=10.0, N::Int=10^5, seed::Int=0; T_min::Float64=-5.0, T_max::Float64=10.0)
  resolvent = Vector{Float64}(undef, iter)

  for (i, x₀) in zip(1:iter, range(T_min, T_max, length=iter))
    t, m = calc_BPS_Covariance(N, seed=seed, x₀=x₀)
    e = exp.(-ρ * t)
    resolvent[i] = sum(e .* m) * step(t)
  end
  return range(T_min, T_max, length=iter), resolvent
end

ρ = 1.0
x, r_BPS = calc_BPS_resolvent(ρ)
pᵣ = plot(x, r_BPS, xlabel=L"x", ylabel=L"\int^\infty_0e^{-\rho t}\operatorname{E}_x[X_t]\,dt", label="BPS", title="Resolvent (ρ=$ρ)", linewidth=3, left_margin=4Plots.mm, top_margin=1Plots.mm)
pᵣ
function calc_FECMC_resolvent(ρ::Float64=1.0, iter::Int=10, T::Float64=10.0, N::Int=10^5, seed::Int=0; T_min::Float64=-5.0, T_max::Float64=5.0)
  resolvent = Vector{Float64}(undef, iter)

  for (i, x₀) in zip(1:iter, range(T_min, T_max, length=iter))
    t, m = calc_covariance(N, seed=seed, x₀=x₀)
    e = exp.(-ρ * t)
    resolvent[i] = sum(e .* m) * step(t)
  end
  return range(T_min, T_max, length=iter), resolvent
end

x, r_FECMC = calc_FECMC_resolvent(ρ)
plot(pᵣ, x, r_FECMC, xlabel=L"x", ylabel=L"\int^\infty_0e^{-\rho t}\operatorname{E}_x[X_t]\,dt", label="FECMC", title="Resolvent (ρ=$ρ)", linewidth=3)

なぜか，\(X_0=x_0\ll0\) からスタートした際は，条件付き期待値 \(\operatorname{E}_{x_0}[X_t]\) の decay は似通うようである．このときの resolvent の値の差の平均が，\(\sigma(\rho)^2\) の差とほとんど等しい：

diff = r_FECMC - r_BPS
plot(x, diff, xlabel=L"x", ylabel="Difference of Resolvent (ρ=$ρ)", legend=false, linewidth=3, left_margin=1Plots.mm, top_margin=1Plots.mm)

まさかであるが，負領域ではわずかに BPS の場合が値が大きい！しかし平均的に見た場合，特に \(x\ge0\) の領域では FECMC の圧勝である．

\(\rho=1.5\) としても全く同様．別で１時間ほど計算した，grid 数 500 の場合を次に示す：

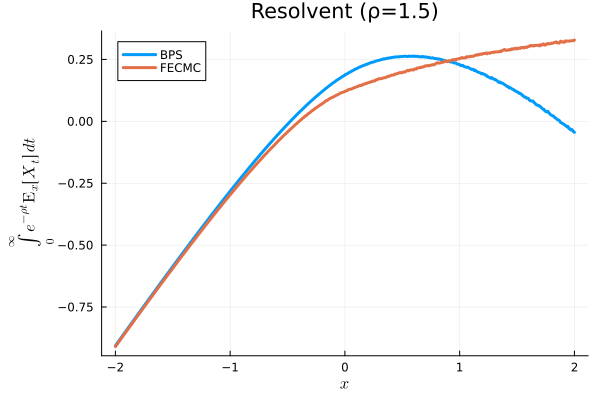
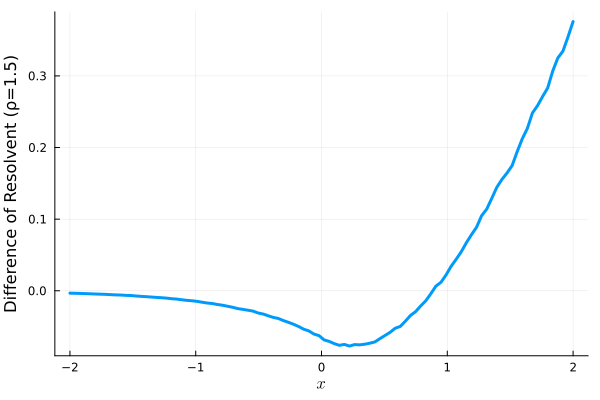
function check_resolvent_difference_at(x₀::Float64=-0.5, ρ::Float64=0.5; T::Float64=10.0, N::Int=10^5, seed::Int=0)
  t, m = calc_covariance(N, seed=seed, x₀=x₀)
  e = exp.(-ρ * t)
  resolvent_FECMC = sum(e .* m) * step(t)
  t, m = calc_BPS_Covariance(N, seed=seed, x₀=x₀)
  resolvent_BPS = sum(e .* m) * step(t)
  return resolvent_FECMC - resolvent_BPS
end

check_resolvent_difference_at(-0.5)
-0.13100228327796445
t, m = calc_covariance(x₀=-1.0)
p = plot(t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=-1.0]", label="FECMC", linewidth=3, size=(800, 400), left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))

t, m = calc_BPS_Covariance(x₀=-1.0)
plot!(p, t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=-1.0]", label="BPS", linewidth=3, left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))
p
-0.2575820778204064-0.0011290642544532692
t, m = calc_covariance(x₀=-3.0)
p = plot(t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=-3.0]", label="FECMC", linewidth=3, size=(800, 400), left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))

t, m = calc_BPS_Covariance(x₀=-3.0)
plot!(p, t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=-3.0]", label="BPS", linewidth=3, left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))
p
-4.244968595389094-4.006646672903708

一方で正に大きな初期値 \(X_0=x_0\gg0\) を与えると，FECMC の方が顕著に速く混ざる：

t, m = calc_covariance(x₀=10.0)
p = plot(t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=10.0]", label="FECMC", linewidth=3, size=(800, 400), left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))

t, m = calc_BPS_Covariance(x₀=10.0)
plot!(p, t, m, xlabel=L"t", ylabel=L"\operatorname{E}[X_t|X_0=10.0]", label="BPS", linewidth=3, left_margin=5Plots.mm, bottom_margin=3Plots.mm)
print(sum(m) * step(t))
p
0.28391707562615554-49.93636424905652

5 Discussion

今回はプロットで示したが，この程度の収束性の違いでさえ数学的に議論するには大変苦労する．hypocoercivity の理論が必要になる．

References

Bierkens, J., Kamatani, K., and Roberts, G. O. (2022). High-dimensional scaling limits of piecewise deterministic sampling algorithms. The Annals of Applied Probability, 32(5), 3361–3407.