統計的検定の考え方と,その科学的な態度については,(大塚淳, 2020, pp. 97–106 ) が大変含蓄が深い.
シリーズトップページはこちら .
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
仮設検定
二項モデルでの検定
冠動脈バイパス手術を受けた20歳の青年が3日後に死亡した.
同病院では過去3年の30件のうち10人が術後1週間以内に死亡している.
一般に術後1週間以内に死亡する確率は0.2である.
不審だと言えるだろうか?言えるとしたらどのような意味で?
「正常な範囲内の事象である」とする帰無仮説の下で,当該事象が起こる確率を計算する.これが5%以下だったら「不審だと思うに足る」と言えるだろう.
本問題は死亡率 \(p\in[0,1]\) という母数に関する検定問題と捉えることができ,すると帰無仮説は \[
H_0:p=0.2
\] というシンプルな表示を得る.
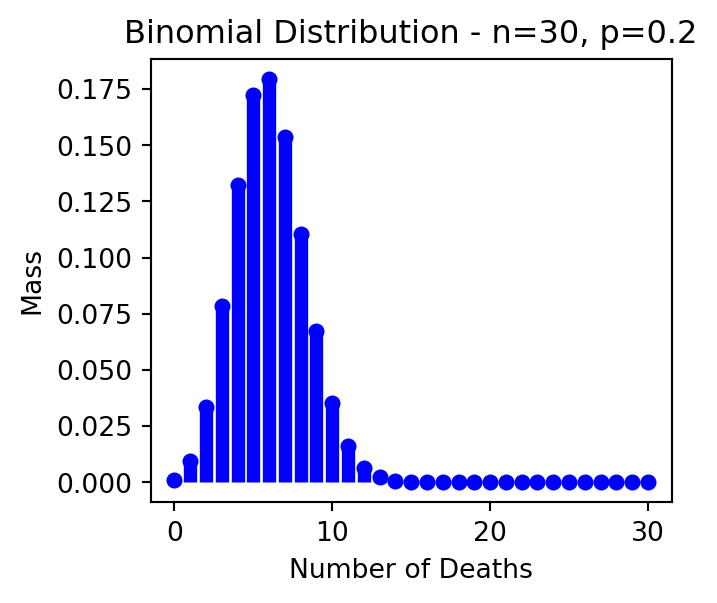
この下で,\(n=30\) として,確率変数 \(X\) を「術後1週間以内に死亡する人数」とすると,\(X\) は二項分布 \(\mathrm{Bin}(30,0.2)\) に従う(二項分布の定義は Section 2.1 ).
Code
import matplotlib.pyplot as pltimport numpy as npfrom scipy.stats import binom# Parameters for the binomial distribution = 30 # number of trials = 0.2 # probability of success in each trial # Generating data for the binomial distribution = np.arange(0 , n+ 1 )= binom.pmf(x, n, p)# Plotting the binomial distribution = (3.5 , 3 ))'bo' , markersize= 5 )0 , y, colors= 'b' , lw= 5 )'Binomial Distribution - n=30, p=0.2' )'Number of Deaths' )'Mass' )False )
この図からも,10人以上になる確率は極めて小さいことが判るだろう.実際に計算してみると,
Code
= 1 - binom.cdf(9 , n, p) - binom.pmf(10 , n, p)/ 2 print (f"p-value is { prob_10_or_more:.4f} " )
となる.この「帰無仮説 \(H_0\) (今回は「1週間死亡率は20%」)を仮定した下で,実際に観測した事象(今回は「30人のうち10人が一週間死亡」)が起こる条件付き確率」を \(p\) -値
上で叙述したのは,「死亡者数」という離散確率変数を検定統計量に用いた場合である.しかし,本書 (草野耕一, 2016, p. 99 ) では,別の離散検定統計量に対して,正規近似を通じて計算している.これは \(z\) -検定と呼ばれるものである( Wikipedia も参照).
計算機が得意ならば,直接計算で出した方が近似誤差がないため,好ましいだろう.実際,書籍で得られた値は \(p=0.0344\) であり,過小評価している.その論拠は「\(pn,(1-p)n\) のいずれも \(5\) 以上であれば正規分布と同一視して良いことが知られている」という点である.
一方で,上の議論では \(p=0.0611\) と5%の水準を超えている.一方で,(Lancaster, 1961 ) の mid-\(P\) value と呼ばれる補正法を用いると \(p=0.0434\) となり,再び有意になる.
このことをどう評価するべきか…….技術的・専門的すぎてとても人口に膾炙するものではないと思うと同時に,非常に本来的ではない議論になっていると感ずる( Section 1.5 ).
誤り
帰無仮説を間違えて棄却してしまうことを,第一種の過誤 \(\alpha\) の値に一致する.
統計的仮説検定の理論は,初めは Neyman と Pearson によって科学的発見の文脈で考えられたものであるため,帰無仮説の棄却は「科学的発見の萌芽」と同義と解すことが多い((大塚淳, 2020, pp. 97–106 ) も参照).その場合,第一種の誤りとは「本当はなんでもないのに大発見だと思い上がりってしまう確率」である.これを犯す確率を最も制限したい,という志向を持つ.
次に,第一種の誤りの可能性 \(\alpha\) を制限した上で,本当は帰無仮説が誤りなのに棄却できないリスク=発見を検出できないリスクをなるべく下げることを二次的目標として考える.これを 第二種の過誤 という.その確率 \(1-\beta\) に対して,\(\beta\) を 検出力 (power) と呼ぶ.
これは 第二回で扱った検察官の誤謬 に通じる語用法である.
独立性の検定
次の条件を持つ学習教材が「必ず英語の成績が上がる」と言えるだろうか?
全国共通模試で,英語の全国平均点は58点であった.
当該教材を用いて勉強した者80名の平均は70点であり,標準偏差は15であった.
これは,当該教材を用いた群と用いていない群という「2つの標本」の間に差がないこと,今回では「平均が同じであること」を帰無仮説として,目下の証拠からこれを棄却出来るかを検定する問題として捉えることができる.
ベイズ統計学
伝統的統計学は客観確率を用いているので,母数の確からしさを1つの数値として示すことができない.伝統的統計学が示しうるものは,「母数がある範囲内にあればこの証拠が現れる確率はいくらであるか」でしかないのである.この矛盾をいかに克服するかは法律家と統計学者が共同して取り組むべき今後の課題であるが,1つの可能性として考えうることは伝統的統計学に代えてベイズ統計学の手法を用いることである .(草野耕一, 2016, p. 119 )
定義集
\[
[a,b]:=\left\{x\in\mathbb{R}\mid a\le x\le b\right\}
\] は実数の区間を表す. \[
\mathbb{N}^+:=\left\{1,2,3,\cdots\right\}
\] は正の整数全体の集合を表す.詳しくは 本サイトの数学記法一覧 を参照.
二項分布
(草野耕一, 2016, p. 92 ) も参照.
パラメータ \(n\in\mathbb{N}^+\) と \(p\in[0,1]\) に関する 二項分布 \(\mathrm{Bin}(n,p)\) とは,集合 \(\{0,1,\cdots,n\}\) 上の離散確率分布で, 確率質量関数 \[
b(x;n,p):=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x},
\] \[
x=0,1,\cdots,n,
\] が定めるものをいう.
パラメータ \(p\in[0,1]\) に関する Bernoulli分布 \(\mathrm{Ber}(p)\) とは,\(n=1\) の場合の二項分布 \[
\mathrm{Ber}(p):=\mathrm{Bin}(1,p)
\] をいう.
ただし,二項係数 \(\begin{pmatrix}n\\x\end{pmatrix}\) は高校数学では \({}_nC_x\) と表す場合が多い.前者の記法の美点は,関係式 \[
\begin{align*}
\begin{pmatrix}n\\x\end{pmatrix}&=\frac{n!}{x!(n-x)!}\\
&=\frac{n}{x}\frac{(n-1)!}{(x-1)!(n-x)!}\\
&=\frac{n}{x}\begin{pmatrix}n-1\\x-1\end{pmatrix}
\end{align*}
\] が直感的に表せる点にある.
References
Lancaster, H. O. (1961). Significance tests in discrete distribution. Journal of the American Statistical Association , 56 (294), 223–234.
大塚淳. (2020).
統計学を哲学する . 名古屋大学出版会.
草野耕一. (2016).
数理法務のすすめ . 有斐閣.