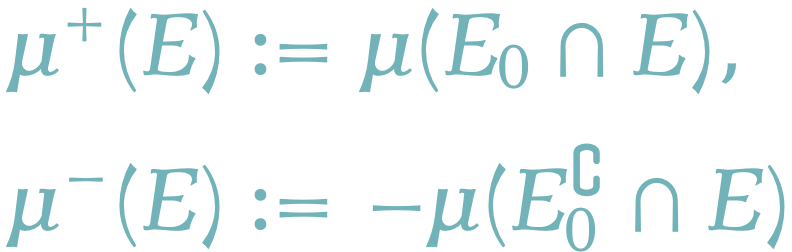「有界」測度と「有限」測度 | Between ‘Bounded’ Measures and ‘Finite’ Measures

Functional Analysis
Author

司馬博文

Published

12/02/2023

Modified

1/01/2024

Abstract
They are the same mathematical object. Let’s step back to view the big picture.

\(B\) をBanach空間または拡張実数 \([-\infty,\infty]\) とする．可測空間 \((S,\Sigma)\) 上の \(B\)-値 \(\sigma\)-加法的関数 \(\mu:\Sigma\to B\) を考える．

この設定の下で，\(B=[-\infty,\infty]\) のときに有限（＝\(\mathbb{R}\)-値）であること，有界であること，有界変動である（全変動が有限）ことの３概念がどのように関係するかを見る．

まとめ
  1. 符号付き測度1 \(\mu:\Sigma\to[-\infty,\infty]\) は，有限ならば有界であり（ 1 ），有界ならば有限である．
  2. 符号付き測度 \(\mu\) が有界であることと，有界変動であることは同値である．値域 \(B\) が有限次元 Banach 空間である場合でも同値である．
  3. 符号付き測度は上に有限ならば上に有界である，というような結果も直接示せる（ 3 ）．
  4. \(\sigma\)-加法性まではいかず，有限加法性しか満たさない場合，有限でも有界とは限らない．2 \(\sigma\)-加法的でも \(\Sigma\) が代数に過ぎない場合も同様．3
  5. \(B\) が有限次元 Banach 空間であるとき \(\mu:\Sigma\to B\) は自動的に有界変動になり（ 4 ），特に有界である．しかし，\(B\) が無限次元の場合は有界変動とは限らないが，有界ではある．4

Jordan Decomposition

1 Jordan分解からの理解

Jordan分解より，符号付き測度 \(\mu:\Sigma\to[-\infty,\infty]\) が関数として有界であることと，全変動が有限（＝\(\mathbb{R}\)-値）になること（有界変動であること）とは同値になる．

定理 (Hahn, 1921)

\((S,\Sigma)\) を可測空間，\(\mu:\Sigma\to[-\infty,\infty]\) を符号付き測度とする．このとき，ある可測集合 \(E_0\in\Sigma\) が存在して，\(\mu:E_0\cap\Sigma\to[0,\infty]\) は非負で，\(\mu:E_0^\complement\cap\Sigma\to[-\infty,0]\) は非正である．

証明は (藤田宏，吉田耕作, 1991, p. 385) 定理7.2，(Dunford and Schwartz, 1958, p. 129) 定理III.4.10, (Dudley, 2002, pp. 178–179) 定理5.6.1 など．(Bogachev and Smolyanov, 2020, p. 72) 定理2.6.1, (Lang, 1993, p. 203) 系VII.3.6 も同様だが，\(\mathbb{R}\)-値の場合に限って証明を与えている．

系5 （Jordan分解）

\((S,\Sigma)\) を可測空間，\(\mu:\Sigma\to[-\infty,\infty]\) を符号付き測度とする．このとき， \[ \mu^+(E):=\mu(E_0\cap E), \] \[ \mu^-(E):=-\mu(E_0^\complement\cap E) \] はHahn分解 \(E_0\in\Sigma\) の取り方に依らずに定まる測度となる．

系2 (Hahn) \(\Phi(E)\) が最大値 \(+\infty\) をとれば，\(\Phi(E)\) の最小値は \(>-\infty\)．また \(\Phi(E)\) が最小値 \(-\infty\) をとれば \(\Phi(E)\) の最大値は \(<+\infty\)．とくに \(\Phi(E)\) が有限であるならば（すなわち有限値しかとらないならば），\(\Phi\) の値域 \(\{\Phi(E)\mid E\in\mathcal{M}\}\) は有界である．(藤田宏，吉田耕作, 1991, p. 389)

2 有界変動性と有界性

前節では有界性（値域が \(\mathbb{R}\) の有界集合になること）を証明したが，符号付き測度ではこれは有界変動性（全変動が有限＝有界）と同値である．

定理（全変動）

\((S,\Sigma)\) を可測空間，\(\mu:\Sigma\to[-\infty,\infty]\) を符号付き測度とする．このとき，次が成り立つ： \[ \begin{align*} &\nu^+(E)+\nu^-(E)\\ &=\sup\left\{\sum_{k=1}^n\lvert\nu(E_k)\rvert\in[0,\infty]\:\middle|\:\substack{n\in\mathbb{N}^+,\{E_k\}\subset\mathcal{E}\;\text{は}\\E\;\text{の分割}}\right\}. \end{align*} \] これを \(\nu\) の 全変動 と呼び，\(\lvert\nu\rvert\) で表す．

例6 （全変動）

\((S,\Sigma,\nu)\) を測度空間とする．

  1. \(\lvert\nu\rvert=\nu\) である．特に，この場合有界測度と有界変動測度の概念は一致する．
  2. \(f\in L^1(\nu)\) について， \[ F(E):=\int_Ef(x)\,\nu(dx),\qquad E\in\Sigma, \] は \(\sigma\)-加法的関数である．この全変動は \[\lvert F\rvert(E)=\int_E\lvert f(x)\rvert\,\nu(dx).\]
  3. 全変動 \(\lvert\nu\rvert:\Sigma\to[0,\infty]\) は \[\|\nu(E)\|\le\lambda(E),\qquad E\in\Sigma,\] を満たす \(\sigma\)-加法的関数 \(\lambda\) のうち最小のものである．

3 直接の証明

命題7 （有限ならば有界）

\((S,\Sigma)\) を可測空間，\(\mu:\Sigma\to[-\infty,\infty)\) を \(\sigma\)-加法的な集合関数とする．このとき，\(\mu\) は上に有界である．

証明

仮に \(\mu\) は上に有界ではないと仮定して，矛盾を導く．可測集合 \(E_1\in\Sigma\) が非有界集合であるとは， \[\sup_{E\in\Sigma}\mu(E\cap E_1)=+\infty\] が成り立つこととすると，仮定より，少なくとも全体集合 \(S\) は非有界である．ここで，

  1. 任意の非有界集合は，任意に大きな測度を持つ非有界部分集合を持つ．
  2. ある非有界集合 \(F\in\Sigma\) が存在して，ある \(N\in\mathbb{N}\) よりも大きな測度を持つ \(F\) の非有界部分集合は存在しない．

の２つの場合に分けられる．

  1. このとき，減少列 \(\{E_n\}\subset\Sigma\) であって \(\mu(E_n)\ge n\;(n\in\mathbb{N}^+)\) を満たすものが取れる．このとき，\(\sigma\)-加法性から \[ \begin{align*} &\mu\left(\bigcap_{i=1}^\infty E_i\right)+\sum_{i=n}^\infty\mu(E_i\setminus E_{i+1})\\ &\qquad=\mu(E_n) \end{align*} \] が成り立つが，仮定より \(\mu(E_n)<\infty\) だから，左辺の第二項の無限和は任意の \(n\in\mathbb{N}^+\) について収束することがわかる．よって，\(n\to\infty\) の極限を考えることで右辺は発散するから，左辺も第一項が発散している必要がある： \[\mu\left(\bigcap_{i=1}^\infty E_i\right)=\lim_{n\to\infty}\mu(E_n)=\infty.\] これは \(\bigcap_{i=1}^\infty E_i\in\Sigma\) に矛盾．
  2. 条件を満たす \(F\in\Sigma\) を取り，ある可測部分集合 \(F_1\subset F\) は \(\mu(F_1)=\mu(F_1\cap F)>N\) を満たすとする．すると \(F_1\) は有界である必要があるが，\(F\) は非有界としたから，\(F\setminus F_1\) が非有界である必要がある．よって可測部分集合 \(A_1\subset F\setminus F_1\) で \(\mu(A_1)\ge1\) を満たすものが取れる．すると \(F_2:=F_1\cup A_1\) も \(\mu(F_2)\ge\mu(F_1)>N\) より，やはり有界である必要がある．これを繰り返すことで， \[\mu\left(\bigcup_{i=1}^\infty A_i\right)=\infty\] を満たす \(\{A_i\}_{i\in\mathbb{N}^+}\subset\Sigma\) が見つかってしまう．
系（ベクトル値測度も有限）

\(B\) をBanach空間，\(\mu:\Sigma\to B\) を \(\sigma\)-加法的関数とする． このとき，\(\mu\) の値域は有界である． しかし，\(\lvert\mu\rvert\) が有限とは限らないことに注意．

4 一般のベクトル値測度の場合

一般の Banach 空間値の \(\sigma\)-加法的集合関数について，値域が有限次元であるならば自動的に有界になることが示せる．

命題8 （有限ならば有界）

\((E,\mathcal{E})\) を可測空間，\(B\) をBanach空間，\(\nu:\mathcal{E}\to B\) を可算加法的集合関数とする．

  1. 全変動 \(\lvert\nu\rvert:\mathcal{E}\to[0,\infty]\) も測度である．
  2. \(B\) が有限次元ならば，\(\lvert\nu\rvert\) は有限である．特に，\(\mu\) は有界である．
証明

仮に \(\lvert\nu\rvert(E)=\infty\) と仮定して矛盾を導く．\(B=\mathbb{R}\) として示せば，あとは成分ごとに考えることで一般次元の場合も同様である．

\(A_1:=E\) から始まる減少列を定める．全変動の定義から，ある部分集合 \(B\in\mathcal{E},B\subset A_1\) が存在して， \[\lvert\nu(B)\rvert\ge\lvert\nu(A_1)\rvert+2\] を満たす．\(\lvert\nu\rvert(B)=\infty\) のとき \(A_2:=B\) とし，\(\lvert\nu\rvert(B)<\infty\) のとき\(A_2:=A_1\setminus B\) とすると， \[\lvert\nu\rvert(A_1\setminus B)=\lvert\nu\rvert(A_1)-\lvert\nu\rvert(B)=\infty.\] このとき，三角不等式から，どちらの場合も \[\lvert\nu(A_2)\rvert\ge\lvert\nu(B)\rvert-\lvert\nu(A_1)\rvert\ge2.\] これを繰り返すことで，\(\lvert\nu(A_n)\rvert\ge n\;(n\in\mathbb{N}^+)\) を満たす減少列 \(\{A_n\}_{n=1}^\infty\) を得る．するとこの極限 \(A:=\bigcap_{n=1}^\infty A_n\) の測度は発散するが，これは \(\nu\) が \(B\)-値であることに矛盾する．よって，\(\lvert\nu\rvert\) は有限である．

反例9 （無限次元の場合）

\(B=l^2\) など無限次元の場合，\(\nu\) が \(B\)-値であっても，その全変動 \(\lvert\nu\rvert\) は発散し得る． これは \(E\) 上のノルムが同値になるとは限らないためである．

証明

\(X=\mathbb{R}_+\) とし，その上の（\([n-1,n]\) 上の）測度を，Lebesgue 測度 \(\ell\) を通じて \[ \nu_n(A):=\frac{1}{n}\ell(A\cap[n-1,n]), \] \[ n\in\mathbb{N}^+,A\in\mathcal{B}(\mathbb{R}_+)_{\ell}, \] と定め，\(\nu(A)_n:=\nu_n(A)\) とすると，確かに \(\nu(A)\in l^2\)： \[ \begin{align*} \|\nu(A)\|_2&=\sqrt{\sum_{n=1}^\infty\biggr(\frac{\ell(A\cap[n-1,n])}{n}\biggl)^2}\\ &\le\sqrt{\sum_{n=1}^\infty\frac{1}{n^2}}<\infty. \end{align*} \] 一方で，全変動は発散する： \[ \begin{align*} \lvert\nu\rvert(\mathbb{R}_+)&=\sum_{n=1}^\infty\lvert\nu_n([n-1,n])\rvert\\ &=\sum_{n=1}^\infty\frac{1}{n}=\infty. \end{align*} \]

では，ベクトル値測度の有界性は何と同値であるかというと，有界半変動性 (bounded semivariation) という有界変動性よりも弱い概念と同値になる．(Diestel and Uhl Jr., 1977) 参照．

References

Birkhoff, G. (1935). Integration of functions with values in a banach space. Transactions of the American Mathematical Society, 38(2), 357–378.
Bogachev, V. I., and Smolyanov, O. G. (2020). Real and functional analysis,Vol. 4. Springer Cham.
Diestel, J., and Uhl Jr., J. J. (1977). Vector measures,Vol. 15. American Mathematical Society.
Dudley, R. M. (2002). Real analysis and probability,Vol. 74. Cambridge University Press.
Dunford, N., and Schwartz, J. T. (1958). Linear operators. Part 1: General theory,Vol. VII. Interscience Publishers.
Giesy, D. P. (1970). A finite-valued finitely additive unbounded measure. The American Mathematical Monthly, 77(5), 508–510.
Hahn, H. (1921). Theorie der reellen funktionen. Julius Springer, Berlin.
Halmos, P. R. (1950). Measure theory,Vol. 18. Springer New York.
Lang, S. (1993). Real and functional analysis,Vol. 142. Springer New York.
Rudin, Walter. (1987). Real and complex analysis. McGraw Hill.
藤田宏，吉田耕作. (1991). 現代解析入門. 岩波書店.

Footnotes

  1. ここで符号付き測度とは，\(\sigma\)-加法的な集合関数 \(\mu:\Sigma\to[-\infty,\infty]\) であって，値域には \(\infty,-\infty\) のいずれか一方しか含まれないもの，としている．数学記法一覧 も参照．↩︎

  2. (Giesy, 1970)↩︎

  3. (Dudley, 2002, p. 181) 命題5.6.4．↩︎

  4. (Dunford and Schwartz, 1958, p. 127) III.4.5．IIII.10.2 p.319 も参照．↩︎

  5. (Dunford and Schwartz, 1958, p. 130) では，有限なJordan測度に関連する分解をJordan分解，有限とは限らない測度に関する分解をHahn分解と呼び分けているが，現代では空間の分解をHahn，測度の分解をJordanと呼び分けることが主流であるようである．(Halmos, 1950) も後者．↩︎

  6. (1), (3)は (Dunford and Schwartz, 1958, p. 97)．(2)は (藤田宏，吉田耕作, 1991, p. 389) 例7.1，(Rudin, 1987, p. 125) 6.13．↩︎

  7. (Dunford and Schwartz, 1958, p. 127) 補題III.4.4 参照．↩︎

  8. (Lang, 1993, pp. 定理3.2 p.197)．↩︎

  9. (Lang, 1993, p. 198). (Birkhoff, 1935) も参照．↩︎