Gamma 確率変数と,その変換として得る Beta 確率変数とに関する次の命題の証明を与える(第 3 節).
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
\(Y_i\sim\mathrm{Gamma}(\alpha,\nu_i)\;(i=1,2)\) は独立とする.このとき,2つの確率変数 \[X_1:=\frac{Y_1}{Y_1+Y_2},\qquad X_2:=Y_1+Y_2\] も互いに独立で, \[X_1\sim\operatorname{Beta}(\nu_1,\nu_2),\] \[X_2\sim\mathrm{Gamma}(\alpha,\nu_1+\nu_2),\] が成り立つ.
証明に先んじて,Gamma 分布と Beta 分布の性質を,それぞれ第 1 節と第 2 節で見ていく.
最後に,確率分布の変換の計算方法をまとめる(第 4 節).混合分布や複合分布など,特定の可微分変換で密度関数がどう変化するかの計算の基礎となる.
Gamma 分布を見る
定義
可測空間 \((\mathbb{R},\mathcal{B}(\mathbb{R}))\) 上の Gamma分布 \(\mathrm{Gamma}(\alpha,\nu)\;(\alpha,\nu>0)\) とは, 密度関数 \[g(x;\alpha,\nu):=\frac{1}{\Gamma(\nu)}\alpha^\nu x^{\nu-1}e^{-\alpha x}1_{\left\{x>0\right\}}\] が定める分布をいう.実際,\(t=\alpha x\) と変数変換すると, \[
\begin{align*}
&\quad\int_0^\infty \alpha^\nu x^{\nu-1}e^{-\alpha x}dx\\
&=\alpha^\nu\int^\infty_0\left(\frac{t}{\alpha}\right)^{\nu-1}e^{-t}\frac{dt}{\alpha}\\&=\int^\infty_0t^{\nu-1}e^{-t}dt=\Gamma(\nu).\end{align*}
\]
形状
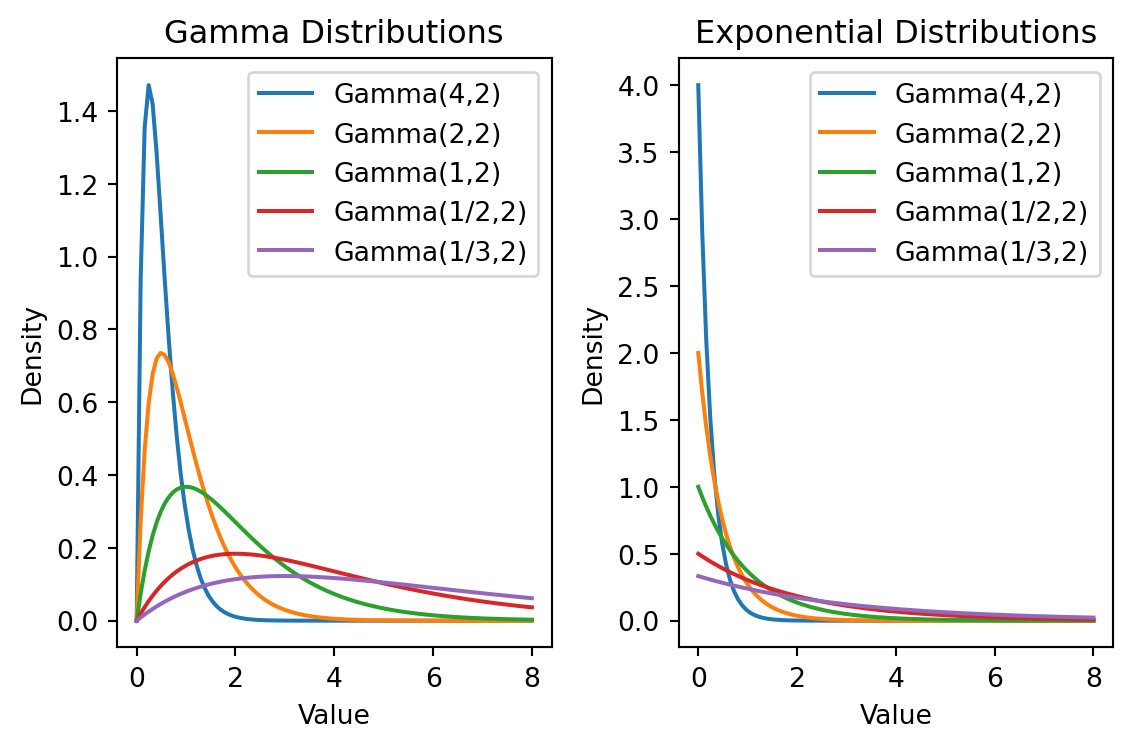
\(\alpha\) をレートパラメータ(スケールパラメータと呼ばれるものの逆数),\(\nu\) を形状パラメータともいう.レートパラメータが大きいほど突起も大きく,手前に寄る.形状パラメータ \(\nu\) は分布の形状を大きく司る.
実際,先度と歪度は形状パラメータのみに依って \[\gamma_1=\frac{2}{\sqrt{\nu}},\qquad\gamma_2=3+\frac{6}{\nu},\] と記述される.
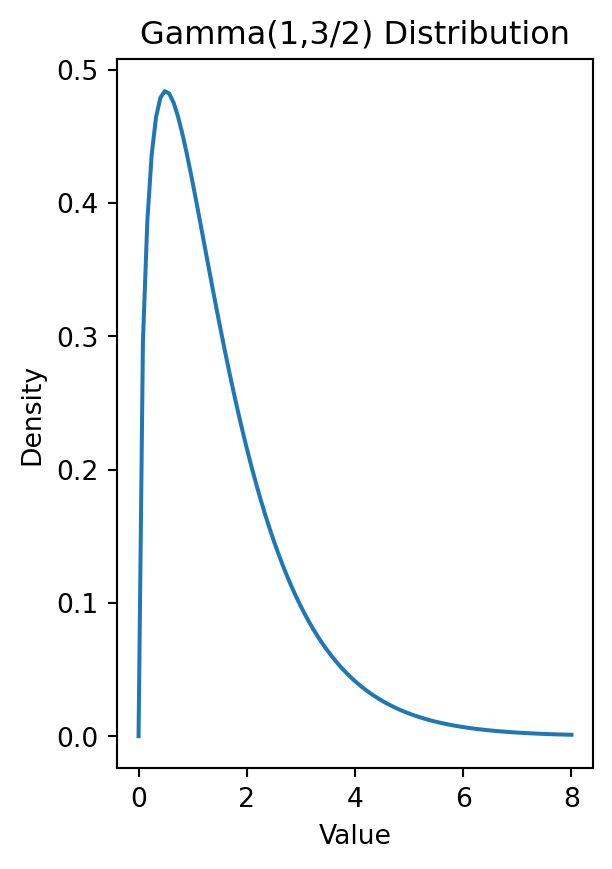
その意味するところを感得するために,scipy.statsでの実装を用いてプロットしてみる.
コードを表示
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
nu = 1.5 # 形状パラメーター
# Gamma分布のPDFをグリッド上で計算
x = np.linspace(0, 8, 100)
pdf = gamma.pdf(x, nu)
# プロットの実行
plt.figure(figsize=(3.2, 4.8)) # スマホサイズに合わせる
plt.plot(x, pdf)
plt.title('Gamma(1,3/2) Distribution')
plt.ylabel('Density')
plt.xlabel('Value')
plt.show()
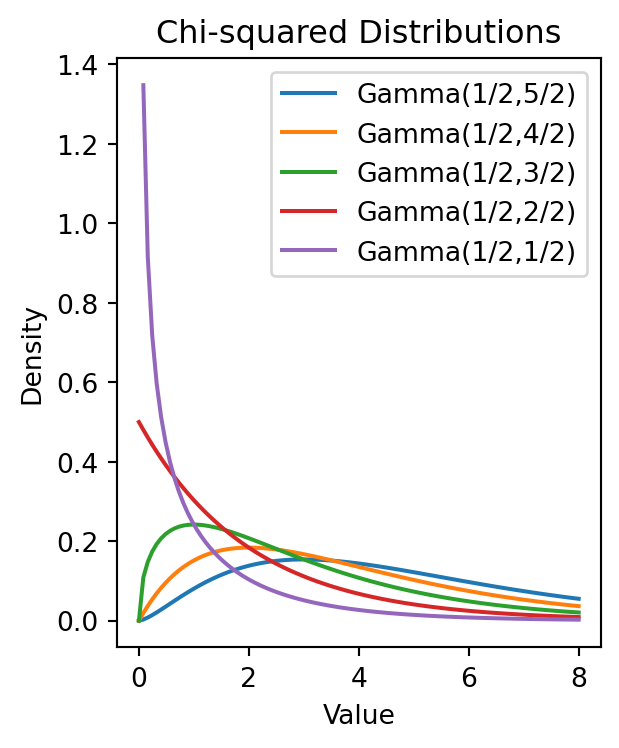
レートパラメータを固定し,形状パラメータを残した \[\chi^2(k):=\mathrm{Gamma}(1/2,k/2)\] を自由度 \(k\) のカイ自乗分布ということに注意.
最後に,レートパラメータが大きいほど突起が大きくなる様子は次の通り:
なお,形状パラメータが \(\nu=1\) である Gamma 分布のことを指数分布という: \[
\operatorname{Exp}(\gamma):=\mathrm{Gamma}(\gamma,1)\;(\gamma>0)
\]
Beta分布を見る
定義
可測空間 \(((0,1),\mathcal{B}((0,1)))\)上の (第1種)ベータ分布 \(\operatorname{Beta}(\alpha,\beta)\;(\alpha,\beta>0)\) とは, 密度関数 \[\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}1_{(0,1)}(x)\] が定める分布をいう.ただし,\[B(\alpha,\beta)=\int^1_0x^{\alpha-1}(1-x)^{\beta-1}\,dx.\]
形状
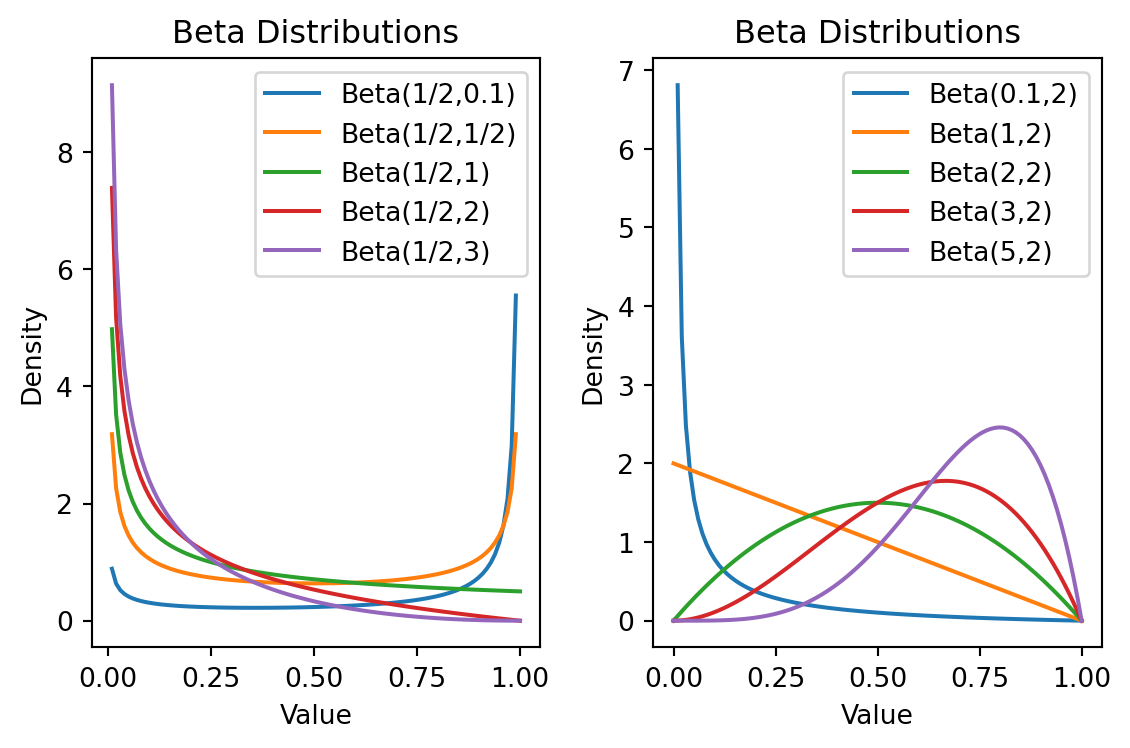
次のような性質を持つ:
- \(\alpha_1=\alpha_2=1\) のとき一様分布となり,\(\alpha_1=\alpha_2>1\) の場合に左右対称な単峰性分布,\(\alpha_1=\alpha_2<1\) の場合に左右対称な U 字型の二峰性分布を得る.
- いずれも \(1\) より大きい場合,左のパラメータが大きい場合 \(\alpha_1>\alpha_2>1\) 左に,右のパラメータが大きい場合 \(\alpha_2>\alpha_1>1\) 右に歪んだ単峰性分布を得る.
- いずれも \(1\) より小さい場合はその逆.
証明
\[\begin{cases}
X_1=\frac{Y_1}{Y_1+Y_2},\\
X_2=Y_1+Y_2.
\end{cases}\] を逆に解くことで, \[\begin{pmatrix}y_1\\y_2\end{pmatrix}=\begin{pmatrix}x_1x_2\\x_2\end{pmatrix}=:T(x_1,x_2)\] を得る.\(A:=(0,1)\times(0,\infty),B:=(0,\infty)^2\) と定めると,\(T:A\to B\) は可微分同相で,Jacobianは \[DT=\begin{pmatrix}x_2&x_1\\0&1\end{pmatrix},\qquad J_T=x_2,\] と計算でき,\(A\) 上で は消えない.
よって \((X_1,X_2)\) の結合分布は \[
\begin{align*}
&p(T(x_1,x_2))J_T(x_1,x_2)dx_1dx_2\\
&=\frac{\alpha^{\nu_1}}{\Gamma(\nu_1)}y_1^{\nu_1-1}e^{-\alpha y_1}\frac{\alpha^{\nu_2}}{\Gamma(\nu_2)}y_2^{\nu_2-1}e^{-\alpha y_2}\\
&\qquad\times\frac{x_2}{(1-x_1)^2}\,dx_1dx_2\\
&=\frac{\alpha^{\nu_1}}{\Gamma(\nu_1)}x_1^{\nu_1-1}x_2^{\nu_1-1}e^{-\alpha x_1x_2}\frac{\alpha^{\nu_2}}{\Gamma(\nu_2)}x_2^{\nu_2-1}\\
&\qquad\times(1-x_1)^{\nu_2-1}e^{-\alpha x_2(1-x_1)}x_2\,dx_1dx_2\\
&=\underbrace{\frac{\Gamma(\nu_1+\nu_2)}{\Gamma(\nu_1)\Gamma(\nu_2)}}_{=B(\nu_1,\nu_2)^{-1}}x_1^{\nu_1-1}(1-x_1)^{\nu_2-1}\,dx_1\\
&\qquad\times\frac{\alpha^{\nu_1+\nu_2}}{\Gamma(\nu_1+\nu_2)}x_2^{(\nu_1+\nu_2)-1}e^{-\alpha x_2}\,dx_2.
\end{align*}
\] これは \(X_1\) が \(\operatorname{Beta}(\nu_1,\nu_2)\) に,\(X_2\) が \(\mathrm{Gamma}(\alpha,\nu_1+\nu_2)\) に独立に従った場合の密度になっている.
余談
総合研究大学院大学統計科学コース2018年8月実施の入試問題の第三問にて,本命題を背景とした問題が出題された.
- 数直線 \(\mathbb{R}\) 上の点Pの \(x\) 座標 \(X\) は \(\mathrm{N}(0,1)\) に従うとする. Pの原点からの距離の自乗の確率密度関数が \[\frac{1}{\sqrt{2\pi x}}e^{-\frac{x}{2}},\qquad(x>0)\] であることを示せ.
- Euclid空間 \(\mathbb{R}^n\) 内の点Qの座標 \((X_1,\cdots,X_n)\) は \(\mathrm{N}_n(0,I_n)\) に従うとする. Qの原点からの距離の自乗の確率密度関数が \[\frac{1}{\Gamma\left(\frac{n}{2}\right)2^{\frac{n}{2}}}x^{\frac{n}{2}-1}e^{-\frac{x}{2}},\qquad(x>0)\] であることを示せ.
- (2)の確率密度関数を持つ分布を \(\chi^2(n)\) という. 確率変数 \(X,Y\) は独立で \(X\sim\chi^2(n),Y\sim\chi^2(m)\) であるとする.このとき, \[X+Y\sim\chi^2(n+m),\] \[\frac{X}{X+Y}\sim\operatorname{Beta}(n/2,m/2),\] であり,互いに独立であることを示せ.
References
Agresti, A. (2012). Categorical data analysis. John Wiley & Sons, Inc.