法律家のための統計数理（４）推測統計学

教科書第３章第１―４節 (pp. 73-96)

草野数理法務
Author

司馬博文

Published

1/11/2024

概要
教科書第３章第１節から第４節 (pp. 73-96) を通じ，統計学検定への入門も兼ねて，推測統計学の基礎を学ぶ．

シリーズトップページはこちら．

1 数学的骨格

詳しくは 本サイトの数学記法一覧 を参照．

1.1 確率空間

定義（確率空間）

  1. 任意の集合 \(\Omega\) に対して，確率の公理 [P1], [P2], [P3] を満たす関数 \[ \operatorname{P}:\left\{\Omega\;\text{の部分集合の全体}\right\}\to[0,1] \] が定義されているとき，組 \((\Omega,\operatorname{P})\) を 確率空間 (probability space) という．

  2. 確率空間上の実数値の関数 \[ X:\Omega\to\mathbb{R} \] を 確率変数 (random variable) という．1

  3. 確率変数 \(X:\Omega\to\mathbb{R}\) に対して， \[ \operatorname{P}^X[A]:=\operatorname{P}[X\in A] \] で定まる実数 \(\mathbb{R}\) 上の分布を，\(X\) の 確率分布 (probability distribution) という．

集合 \(\Omega\) というのを自由にとって良いというのが，確率論の懐の広さであり，統計学で出会う多種多様な問題に対応できる所以である．

サイコロの出目を考える場合は \(\Omega=\{1,2,3,4,5,6\}\) ととってその上の確率空間に関する理論を借りれば良い．殆どの場合は \(\Omega=\mathbb{R}\) と取ることになる．

本当は確率空間は３組 \((\Omega,\mathcal{F},\operatorname{P})\) である．新たに加わった \(\mathcal{F}\) とは何かというと，\(\operatorname{P}\) の定義域であり，上の定義で \[ \operatorname{P}:\left\{\Omega\;\text{の部分集合の全体}\right\}\to[0,1] \] としていたところを \[ \operatorname{P}:\mathcal{F}\to[0,1] \] と，定義域を制限するのが厳密な定義である．

したがって，標本空間 \(\Omega\) の部分集合はなんでも事象と呼んでいいかというと，数学的にはそうではなく，事象の全体 \(\mathcal{F}\) は一定の（代数的な）規則を満たす必要がある（完全加法性 という）．

これは 測度論 (measure theory) と呼ばれる数学分野から得られる知見である．

なぜ制限しなければいけないのか？は，そうしなければ数学的な矛盾が起こるからなのであるが，普通に統計学の目的で確率論を用いる範囲でこの矛盾に遭遇することは滅多にないので，ここでは触れない．

1.2 確率変数の概念

確率変数の概念は，確率論において最も重要なものである．David Mumford というフィールズ賞も受賞した世界的な数学者（専門が確率論というわけではない）も，次のように述べている：

The basic object of study in probability is the random variable and I will argue that it should be treated as a basic construct, like spaces, groups and functions, and it is artificial and unnatural to define it in terms of measure theory. (Mumford, 2000, p. 108)

確率変数が重要な理由は，それは確率分布と違うということを徹底的に教えてくれることにある．換言すれば，日常的な感覚で確率を議論するとなかなかモヤモヤが解消せずに解った気になれない理由は，確率変数と確率分布という本来別々の存在を人間は混同してしまいがちだからからである，と教えてくれるのが現代の確率論なのである．

中高の数学での「場合の数と確率」は特に混同の傾向が強い．三角関数がどのように社会の役に立つか不思議に思ったことがあるならば，あそこで習った初頭的な議論がどう統計学に応用されてどうして AI が生まれるに至ったのかたいへん不思議であろう．中高での離散的な議論を連続な場合にも通用するようにするためには，確率分布と確率変数を峻別することが肝要 である．

確率変数は，「変数」の概念の確率化 である．変数は，高校数学などでも \(x,y,z,\cdots\) と小文字で表したが，確率変数は \(X,Y,Z,\cdots\) と大文字で表す． \(\Omega=\{*\}\) と標本空間を一点集合と取った場合，確率変数は通常の決定論的な変数と同義になる．

一方で，高校数学などでも扱う「関数」の概念の確率化は　確率過程 という．確率過程は名前は仰々しいかも知れないが，定義自体はなんてことはない，確率変数の集合のこと である．

例えば，日付 \(n\) の株価 \(X_n\) の列 \(X_1,X_2,X_3,\cdots\) は確率過程である．決定論的な関数 \(n\mapsto x_n\) の確率化である．

1.3 分布の押し出し

では実際に，確率分布と確率変数がどう違うかを説明する．

確率分布は確率空間に宿るもので，確率変数は確率空間を繋ぐものである．

サイコロを２回振った出目の全体を標本空間とするならば， \[ \Omega:=[6]\times[6]=\left\{(1,1),(1,2),\cdots,(1.6),(2,1),\cdots\right\} \] という集合の上に，一様分布

を定義して得る確率空間を考えるのが一つの良い方法であろう．

これが確率分布である．

一方で，確率変数は，標本空間上の関数の全てである．例えば，出た目の和は確率変数である．

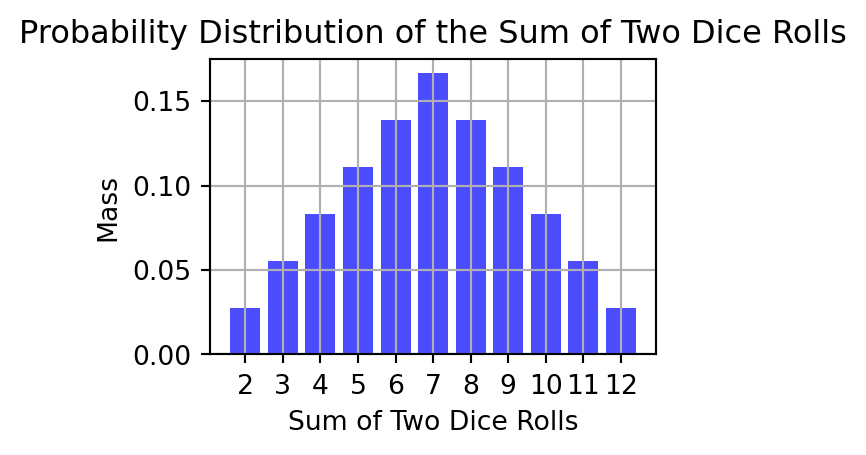
最も重要なことは，確率変数は分布を押し出す ということである．

実際，出た目の和は，確率分布を押し出して，次のような確率分布を定める：

2 今回の内容

数学的骨格を理解した状態で，今回範囲の内容 (草野耕一, 2016, pp. 73–96) を整理する．

2.1 母集団と標本 (pp.73-75)

2.1.1 母集団

標本調査が行われるとき，調査対象となる全体集団を 母集団 (population) という．全人口を精査することは困難であるため，ここから無作為に一部分を選ぶことになる．これを 標本調査 (survey sampling) といい，得られたデータを 標本 (sample) という．

すなわち，データとは確率変数 \(X_1,\cdots,X_n\) であり，これらの積が定める確率変数 \[ X=(X_1,\cdots,X_n):\Omega\to\mathbb{R}^n \] を考え，母集団を \(\Omega\) とし，確率変数 \(X_1,\cdots,X_n\) を標本とするのである．

\(X_1,\cdots,X_n\) が，母集団となる確率空間 \((\Omega,\operatorname{P})\) に関する情報をなるべく効率よく伝えてくれるように設計するのが重要である．実際，現代の標本調査では，無作為抽出が基本であり，一昔前では電話番号台帳の下一桁を無作為に選び，電話を掛けるという方法が用いられた．当然この場合，電話を持っていない標本 \(\omega\in\Omega\) についての情報は得られないので，その点に関する補正が必要になる，という具合である．

このように，「無作為」と言っても具体的にどのように選べば良いか？を考える分野を 標本調査法 (sampling theory) という．2 大統領選挙を通じての標本抽出法の発展の例は Section 3.2 に付した．

2.1.2 統計量の例

標本の関数を 統計量 (statistic) という．

定義（３つの標本統計量）

\(x_1,\cdots,x_n\) を標本とする．

  1. 次を 標本平均 という： \[ \overline{x}:=\frac{x_1+\cdots+x_n}{n}. \]
  2. 次を 標本分散 という： \[ s^2:=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2. \]
  3. 標本分散の非負の平方根 \(s:=\sqrt{s^2}\) を 標本標準偏差 という．
  4. 次を 不偏分散 という： \[ u^2:=\frac{1}{n-1}\sum_{i=1}^n(x_i-\overline{x})^2. \]
命題（分散公式）

標本分散 \(s^2\) と標本平均 \(\overline{x}^2\) の間には次の関係が成り立つ： \[ s^2=\frac{1}{n}\sum_{i=1}^nx_i^2-\overline{x}^2. \] \(\frac{1}{n}\sum_{i=1}^nx_i^2\) という量を 標本の２次の絶対積率 という．

\[ \begin{align*} s^2&=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2\\ &=\frac{1}{n}\sum_{i=1}^n(x_i^2-2x_i\overline{x}+\overline{x}^2)\\ &=\frac{1}{n}\sum_{i=1}^nx_i^2-2\overline{x}\frac{1}{n}\sum_{i=1}^nx_i+\overline{x}^2\\ &=\frac{1}{n}\sum_{i=1}^nx_i^2-\overline{x}^2. \end{align*} \]

2.1.3 母数とは何か？

本書 (草野耕一, 2016, p. 75) に

標本に統計量があるように母集団にもその特性を表す数値が備わっているはずであり，そのような数値のことを 母数 という．

とあるが，この文脈では母数ではなく 特性値 という (竹村彰道, 2020)．特性値を母数と設定することが多いが，それはあくまで統計解析者の裁量である．

母数とは次に示すように，推定対象として解析者が設定する母集団の特性値 である．標本統計量は実際に計算できるが，特性値と母数は未知である．

よって，ほとんどの場合，推測統計の問題とは母数推定の問題に他ならない．

定義（統計モデル，母数）
  • 母集団上の確率分布の族 \(\{P_\theta\}_{\theta\in\Theta}\) を 統計モデル という．
  • 統計モデルを添字付ける「番号」 \(\theta\in\Theta\) を 母数 という．

真の分布を \(\operatorname{P}\) としたとき，これを近似すると思われる分布族 \(\{P_\theta\}_{\theta\in\Theta}\) を統計解析者が設定するのである．腕の見せ所である．

あなたが保険数理士だとして，重大事故の発生確率を推定する際， \[ \Omega=\left\{0,1,2,\cdots\right\} \] を一定期間内に起こる重大事故件数とすると，これに対する分布族は Poisson 分布族 \(\{\mathrm{Pois}(\lambda)\}_{\lambda>0}\) を取ると近似精度が良いことが知られている．Poisson 分布の母数 \(\lambda>0\) は 到着率 や 強度 と呼ばれる．

2.2 統計推測の技法(1) (pp.75-85)

本書 (草野耕一, 2016, pp. 75–85) の重大な特徴に，確率変数と確率分布を区別していないという問題がある．

確率分布とは 第１回講義 で導入した，３つの公理を満たす集合関数 \(\operatorname{P}:P(\Omega)\to[0,1]\) である．3 このとき，ペア \((\Omega,\operatorname{P})\) を，確率が定義された集合という意味で 確率空間 という．

確率変数 とは，確率空間 \((\Omega,\operatorname{P})\) 上に定義された関数 \(X:\Omega\to\mathbb{R}\) のことである．特に，値域が \(\mathbb{N}\subset\mathbb{R}\) に限る場合を 離散変数 という．

2.2.1 離散の場合

確率変数 \(X\) の取り得る値が \(\mathbb{N}=\{0,1,2,\cdots\}\) に限る場合が離散の場合である．

定義（期待値）
  1. 非負値の関数 \(f:\mathbb{N}\to[0,1]\) であって次を満たすものを 確率（質量）関数 という： \[ f(n)=\operatorname{P}[X=n] \]
  2. 確率関数 \(f:\mathbb{N}\to[0,1]\) に従う確率変数 \(X:\Omega\to\mathbb{N}\) に対して，次の量 \(\operatorname{E}[X]\) を 期待値 という： \[ \operatorname{E}[X]:=\sum_{n=1}^\infty nf(n)=\sum_{n=1}^\infty n\operatorname{P}[X=n]. \]
  3. 次の量 \(\mathrm{V}[X]\) を \(X\) の 分散 という： \[ \mathrm{V}[X]:=\operatorname{E}\biggl[(X-\operatorname{E}[X])^2\biggr]. \]

2.2.2 連続の場合

定義（期待値）

\((\Omega,\operatorname{P})\) を確率空間，\(X:\Omega\to\mathbb{R}\) をその上の確率変数とする．

  1. 非負値の関数 \(F:\mathbb{R}\to[0,1]\) であって次を満たすものを，\(X\) の （累積）分布関数 という： \[ F(x):=\operatorname{P}[X\le x]. \]
  2. 非負値の関数 \(p:\mathbb{R}\to\mathbb{R}_+\) であって次を満たすものが存在するならば，これを \(X\) の （確率）密度関数 という： \[ \operatorname{P}[X\in A]=\int_Ap(x)\,dx. \]
  3. 確率密度 \(p\) に従う確率変数 \(X:\Omega\to\mathbb{R}\) に対して，次の量 \(\operatorname{E}[X]\) が存在するならば，これを \(X\) の 期待値 という： \[ \operatorname{E}[X]:=\int_\mathbb{R}xp(x)\,dx. \]
  4. 次の量 \(\mathrm{V}[X]\) が存在するならば，これを \(X\) の 分散 という： \[ \mathrm{V}[X]:=\operatorname{E}\biggl[(X-\operatorname{E}[X])^2\biggr]. \]

2.2.3 期待値の性質

命題（期待値の性質）

\(X,Y:\Omega\to\mathbb{R}\) を確率変数とする．

  1. （期待値の線型性）任意の \(a,b\in\mathbb{R}\) について， \[ \operatorname{E}[aX+bY]=a\operatorname{E}[X]+b\operatorname{E}[Y]. \]
  2. （分散公式）次が成り立つ： \[ \mathrm{V}[X]=\operatorname{E}[X^2]-(\operatorname{E}[X])^2. \]
  3. （分散の斉次性）任意の \(a,b\in\mathbb{R}\) について， \[ \mathrm{V}[aX+b]=a^2\mathrm{V}[X]. \]
  1. 積分の線型性から従う．
    1. の期待値の線型性のみから従う．

2.2.4 独立性と共分散

定義（確率変数の独立性）

\(X,Y:\Omega\to\mathbb{R}\) を確率変数とする．

  1. \(X,Y\) が互いに 独立 であるとは，任意の事象 \(A,B\subset\Omega\) について， \[ \operatorname{P}[X\in A,Y\in B]=\operatorname{P}[X\in A]\operatorname{P}[Y\in B] \] を満たすことをいう．
  2. \(X,Y\) の 共分散 とは， \[ \mathrm{Cov}[X,Y]:=\operatorname{E}\biggl[(X-\operatorname{E}[X])(Y-\operatorname{E}[Y])\biggr] \] をいう．
命題（独立確率変数の性質）

\(X,Y:\Omega\to\mathbb{R}\) を確率変数とする．

  1. \(X,Y\) が独立ならば，次が成り立つ： \[ \operatorname{E}[XY]=\operatorname{E}[X]\operatorname{E}[Y]. \]
  2. 次が成り立つ： \[ \mathrm{V}[X+Y]=\mathrm{V}[X]+2\mathrm{Cov}[X,Y]+\mathrm{V}[Y]. \]
  3. （独立ならば無相関）\(X,Y\) が独立ならば， \[ \mathrm{Cov}[X,Y]=0. \] 特に，\(X,Y\) が独立ならば，\(\mathrm{V}\) は加法を保存する．
  1. Lebesgue 積分論の議論が必要なので省略する．
    1. のみから従う．式変形は次の通り： \[ \begin{align*} \mathrm{V}[X+Y]&=\operatorname{E}[(X+Y)^2]-\biggr(\operatorname{E}[X]+\operatorname{E}[Y]\biggl)^2\\ &= \end{align*} \]

2.3 統計推測の技法(2) (pp.85-94)

2.3.1 正規分布

Code 
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, FloatSlider
import seaborn as sns

# 正規分布のグラフを描画する関数
def plot_normal_distribution(variance):
    mean = 0  # 平均値
    sigma = np.sqrt(variance)  # 標準偏差（分散の平方根）
    
    # 正規分布のデータを生成
    x = np.linspace(-10, 10, 1000)
    y = (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(- (x - mean)**2 / (2 * sigma**2))
    
    # グラフを描画
    plt.figure(figsize=(3, 2))
    sns.lineplot(x=x, y=y)
    plt.title(f'Normal Distribution with Variance {variance}')
    plt.xlabel('Value')
    plt.ylabel('Probability Density')
    plt.show()

# インタラクティブなウィジェットを作成
interact(plot_normal_distribution, variance=FloatSlider(value=1, min=0.1, max=5, step=0.1))
<function __main__.plot_normal_distribution(variance)>

2.3.2 Bernoulli分布と二項分布

2.3.3 Poisson分布

2.4 統計推測の技法(3) (pp.94-97)

ここで重要なトピックは不偏分散である．

3 補足

3.1 第1節：母集団と標本

3.1.1 「推測統計学」とは何か？

本書 (草野耕一, 2016, p. 73) でも次のような注がなされている：

推測統計学に対して，証拠から得られた情報をいかに効率的かつ明確に表現するかを研究する統計学の分野を記述統計学という (草野耕一, 2016, p. 73)．

現代では「統計学」と言った際にほとんど推測統計学を指すと言っても過言ではない．4 つまり，現代では殆ど形骸化した区別である．この名称の本当の意味を理解するためには，歴史的な情緒を持った文脈が必要である．

一言で言えば，推測統計学は Ronald A. Fisher の理論が出て来た際に，それ以前の Quetelet からの統計学との断絶を強調するために用いられた語であった．

推計学 stochastic は推計と計画のための科学であり，その建設は主として英国の農学者 R. A. Fisher （現在 Cambridge 大学教授）の構想に懸る．–(増山元三郎, 1950, p. 3)

その態度の違いは，次の例が鮮明に示している．

例えば算術平均 mean という概念について：旧来の考え方に従えば平均 average は集団の ‘代表’ 値であると定義されている．5 従って，算術平均が該集団をよく ‘代表’ しうると考えられる場合にはこれを採用し，しからざる場合には度数分布の形を眺めた上で，その他の平均値，例えば並数 mode なり幾何平均 geometrical mean なりをもって，これに代えるのである．だから ‘代表値’ として如何なる平均値を選ぶかは，この際，全く個々人の常識に委ねられてしまう．これに反して推計学が算術平均を採用するのは，それが分布関数として表現せられた母集団の或る常数（即ち母数）の適切な平均値となりうる場合のみに限られる．従来統計学を定義して ‘平均の学である’ となす立場があるけれども（例えば A. L. Bowley）このような考え方こそ統計学の記述的性格を遺憾なく露呈するものであろう．統計学がこのような原理に立つ限り，それは爾後の行動に関し，形式以上に何ら指針を与える力をもちうるものではない．行動の正しい指針を与えないような学問は実は科学の名に値しないものというべきであろう．これにも拘らず推計学は吾国では最近に到るまで，科学・技術の分野でさえ仲々受け入れられず政治・経済の領域では殆ど問題にもされなかったのである．これに反し，米国などでは，推計学が社会・自然のあらゆる分野に進出し，第２次大戦の遂行にあたっても大きな貢献をなしたのであった．–(増山元三郎, 1950, p. 4)

前者の記述統計学的な動機は，現代では「データサイエンス」のような分野に引き継がれている (Hoaglin et al., 2006)．

3.2 Gallup事件

3.2.1 1936年大統領選挙とクオータ抽出の重要性

Roosevelt v.s. Landon (1936)
  • 背景には1929年10月24日の「暗黒の木曜日」に端を発した世界大恐慌があった．
    • 民主党 Franklin D. Roosevelt は再選を目指し，共和党の Alfred Landon が立ち向かった．
    • Roosevelt の保守的な姿勢は大恐慌を食い止めるには力不足と思われ，再選の見込みは低いという意見も強く，The Literary Digest は237万人6 を対象に回収した調査結果から，57% の得票で Landon が勝つだろうと予測した．
  • 一方で Gallup 率いる the American Institute of Public Opinion は3000人の標本から Roosevelt が 55.7% の得票を得て当選するだろう，と予測した．7

結果，Roosevelt が 60% の得票を得て，48州中46州を手にした．

なぜ The Literary Digest は予測を誤ったのか？その原因は不適切な標本抽出法にあった．

  • The Literary Digest は自誌の購読者（大恐慌の最中でも購読した層）を対象に，そして自動車保有者と電話利用者の名簿を使って約1000万人に郵送し，回収された237万人の回答を用いた．
  • 過去5回の大統領選挙で的中させていたのは，経済的な状況があまり投票結果に影響しない時勢だったためと思われる．
  • 一方，Gallup は母集団を層別してサンプルサイズを割り当て，そのクオータに沿って標本を集める非確率的抽出法を用いていた．なお，Gallup は4ヶ月前から，The Literary Digest の予測は外れるだろうと新聞のコラム上で予言していた．

このエピソードは 不適切なデザイン下で収集された大量データよりも良いデザイン下で収集された少量のデータのほうがずっと役に立つ ということの好例として強調されることとなった．

しかし，話はここでは終わらない．その Gallup も，後の大統領選挙で予測を大きく外している．

3.2.2 1948年大統領選挙と無作為抽出の重要性

Truman v.s. Dewwey (1948)
  • 1948年の選挙では，民主党は在任中に斃れた Roosevelt の後を継いでいた Harry Truman，共和党は4年前に Roosevelt に負けた Thomas Dewey が戦った．
  • この年の背景には公民権問題があり，共和党が20年ぶりに政権を奪還すると予想されており，Gallup もその例にもれなかった．

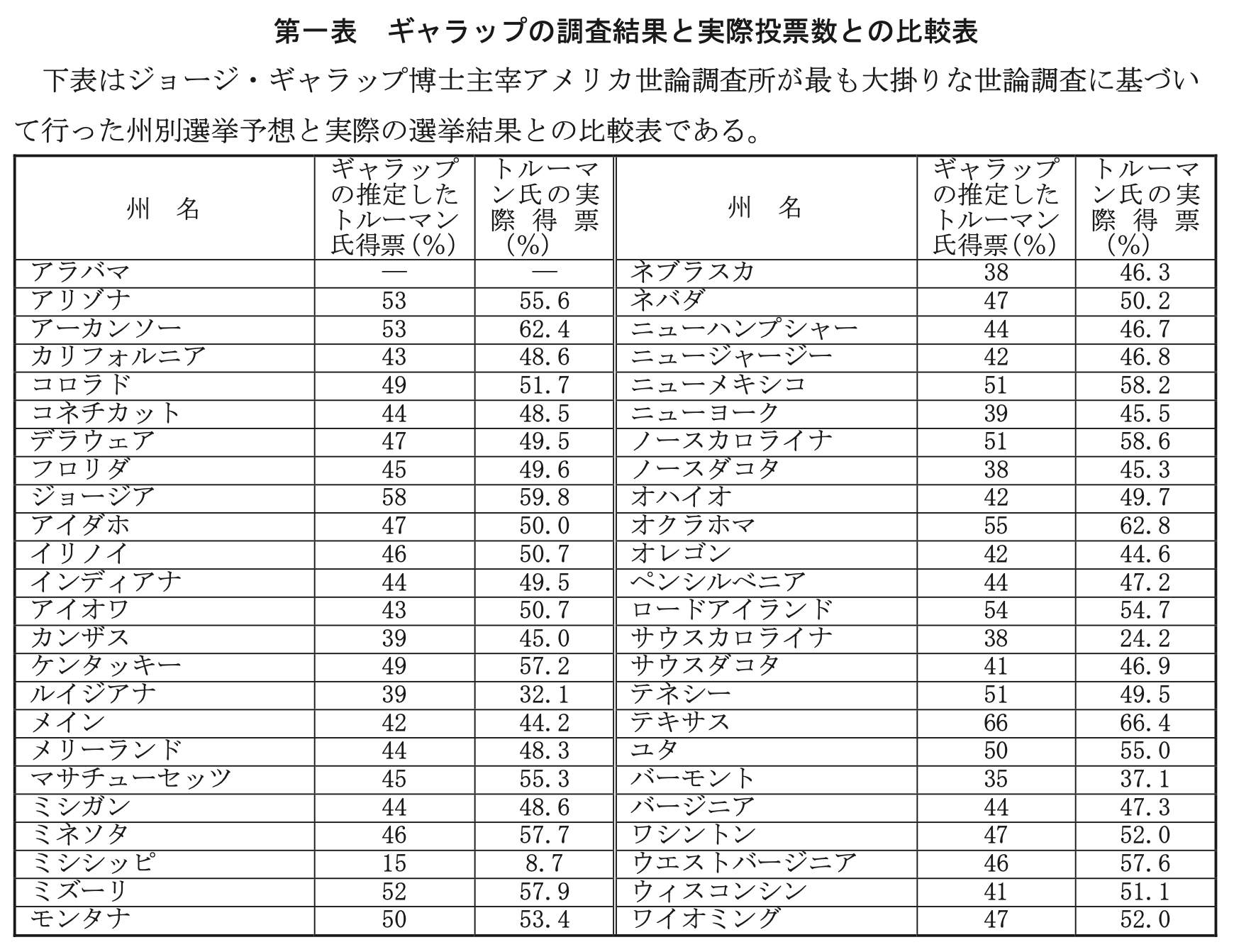
結果，Truman が僅差で Dewey を破って当選した．

なぜクオータ法を用いたサンプリングで実績を出した Gallup は，今回は予測を大きく誤ったのか？

  • 今回 Gallup も予想に失敗して世論調査そのものに懐疑の目が向けられたことを重く見て，検討委員会が設置された．
  • そこで論点となったのが，当時 Gallup が用いていた割当法では，層内の個々の対象者の決定が調査員の個人的判断に委ねられていたことが多きなバイアスの原因となっていると予想された．
  • その結果，今日では 無作為抽出 が大原則として一層強調されるエピソードとなっている (総務省統計局, 2023年4月21日確認)．
  • だがこれ自体が原因だとは言えない．事実，調査担当員もそのことは自覚しており，予測を修正する調整技術を独自に開発して用いていたという (佐藤寧, 2020)．どんな標本調査法にも偏りがあり，これを修正するための予測モデルと併用するという営みは現在の無作為抽出法でも同様であり，これ自体が問題ではない．
  • 当時（現在も）広く用いられている電話調査という手法が，1948年代当時では裕福な有権者（電話を購入することができ，また不変の住所を維持していた）に偏ったサンプル抽出に導いたという議論もある．8

(佐藤寧, 2020, p. 15) より

1947年時点での GHQ による日本への統計指導でも，すでに無作為抽出法（当時は「任意見本法」）による調査が指導されている (佐藤寧, 2020)．よって，当時からクオータ法の問題は認識されており，これに必要な対策を打つ形で運用されていたと解すのが妥当であろう．

なお，日本側のエピソードとして，統計数理研究所第７代所長も務めた 林知己夫 のオーラルヒストリーに次のような一節がある：

そんな時に，CIEの担当官は，日本の新聞社を集めて，「アメリカではクォータサンプルでやっているけれど，そんなのはサンプリングじゃない」と，トルーマン，デューイの大統領選挙の予測を持ち出してきてですね，「これはクォータサンプリングでやったから間違えたんだ．こんなもの夢夢やるんじゃないぞ」と．そうしてみんな肝に銘じたんですよね．サンプリングは厳正にやらなきゃいけないって教わったわけです (高橋正樹, 2004)．

References

Hoaglin, D. C., Mosteller, F., and Tukey, J. W. (Eds.). (2006). Exploring data tables, trends and shapes. John Wiley & Sons.
Jevons, W. S. (1879). Principles of science. Macmillan.
Mumford, D. (2000). The dawning of the age of stochasticity. In Mathematics : Frontiers and perspectives, pages 197–218. American Mathematical Society.
Wu, C., and Thompson, M. E. (2020). Sampling theory and practice. Springer Cham.
中山健夫. (2003). 「代表的な意見」とは何か？―「237万人」と「2万人」. 病院図書館, 23(2), 70–71.
佐藤寧. (2020). 1948年アメリカ大統領選挙予想は何故失敗したか. 日本世論調査協会報「よろん」, 126, 10–16.
増山元三郎. (1950). 推計学への道. 東大協組出版部.
竹村彰道. (2020). 現代数理統計学. 学術図書.
総務省統計局. (2023年4月21日確認2023年4月21日確認). なるほど統計学園 アメリカ大統領選挙の番狂わせ（前編）標本調査における偏り1.
草野耕一. (2016). 数理法務のすすめ. 有斐閣.
鈴木督久. (2021). 世論調査の真実. 日本経済新聞出版本部.
高橋正樹. (2004). 科学史と科学者――林知己夫氏公開インタビュー――. 行動計量学, 31(2), 107–124.

Footnotes

  1. ただし，\(\mathbb{R}\) とは実数の全体からなる集合とした．↩︎

  2. (Wu and Thompson, 2020) など．↩︎

  3. 数学では \(P(\Omega):=\left\{\Omega\;\text{の部分集合の全体}\right\}\) と表す．これを 冪集合 (power set) という．その頭文字の \(P\) である．↩︎

  4. なお，(増山元三郎, 1950) の序によると，推測統計学 という語は北川敏男によるものであり，増山は 推計学 (stochastics) と呼んでいる．↩︎

  5. \(\phi(y,y,\cdots)=\phi(x_1,x_2,\cdots)\) なる関係が成り立つとき，\(y\) を \(x_1,x_2,\cdots\) の平均という．参照：(Jevons, 1879, p. 391)↩︎

  6. (中山健夫, 2003)↩︎

  7. (鈴木督久, 2021) によると，実際はこれは史実の誤解であるようだ．Gallup が「Digest は Landon が 56% だとして予測を誤るだろう」というコラムを新聞社に送付するのに用いた標本が3000なのであって，Gallup 自身の選挙予測調査の標本サイズは30万人であったという．なお，その際の抽出法については歴史的な文献が欠けており，知る由がないという．とは言え，それでも，「標本は量より質」という教訓になる，という意味では，象徴的なエピソードであることは間違いない．↩︎

  8. Wikipedia の記述．↩︎