雑音除去拡散サンプラー

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

関連ページ

1 はじめに

1.1 雑音除去過程サンプラー

DDS (Denoising Diffusion Sampler) は (Vargas et al., 2023) によって提案された，雑音除去過程 (Denoising Process) を用いたサンプリング法である．

雑音除去過程に関しては次の記事を参照：

DDS については次の記事を参照：

本記事では 著者の GitHub を参照にして DDS の実装を吟味する．

1.2 funnel 分布

(Neal, 2003) が slice sampling のデモ用に定義した 漏斗分布 を考える： \[ p(y,x)=\phi(y;0,3)\prod_{i=1}^9\phi(x_i;0,e^{y/2}),\qquad y\in\mathbb{R},x\in\mathbb{R}^9. \]

import jax
from jax.scipy.stats import multivariate_normal
from jax.scipy.stats import norm

import jax.numpy as jnp

def funnel(d=10, sig=3, clip_y=11):
  """Funnel distribution for testing. Returns energy and sample functions."""

  def neg_energy(x):
    def unbatched(x):
      v = x[0]
      log_density_v = norm.logpdf(v,
                                  loc=0.,
                                  scale=3.)
      variance_other = jnp.exp(v)
      other_dim = d - 1
      cov_other = jnp.eye(other_dim) * variance_other
      mean_other = jnp.zeros(other_dim)
      log_density_other = multivariate_normal.logpdf(x[1:],
                                                     mean=mean_other,
                                                     cov=cov_other)
      return log_density_v + log_density_other
    output = jax.vmap(unbatched)(x)
    return output

  def sample_data(n_samples):
    # sample from Nd funnel distribution
    y = (sig * jnp.array(np.random.randn(n_samples, 1))).clip(-clip_y, clip_y)
    x = jnp.array(np.random.randn(n_samples, d - 1)) * jnp.exp(-y / 2)
    return jnp.concatenate((y, x), axis=1)

  return neg_energy, sample_data

import numpy as np
import matplotlib.pyplot as plt

# ファンネル分布のサンプルデータを生成
neg_energy, sample_data = funnel(d=10)
n_samples = 10000  # サンプル数
data = sample_data(n_samples)

# 最初の2次元を抽出（yとx1）
y = data[:, 0]
x1 = data[:, 1]

# 散布図をプロット
plt.figure(figsize=(8, 6))
plt.scatter(y, x1, alpha=0.5, s=1)
plt.xlabel('y')
plt.ylabel('x1')
plt.title('Funnel Distribution (First Two Dimensions)')
plt.grid(True)

# xlim と ylim を追加
plt.xlim(-8, 8)  # x軸の範囲を -10 から 10 に設定
plt.ylim(-7, 7)  # y軸の範囲を -20 から 20 に設定

plt.show()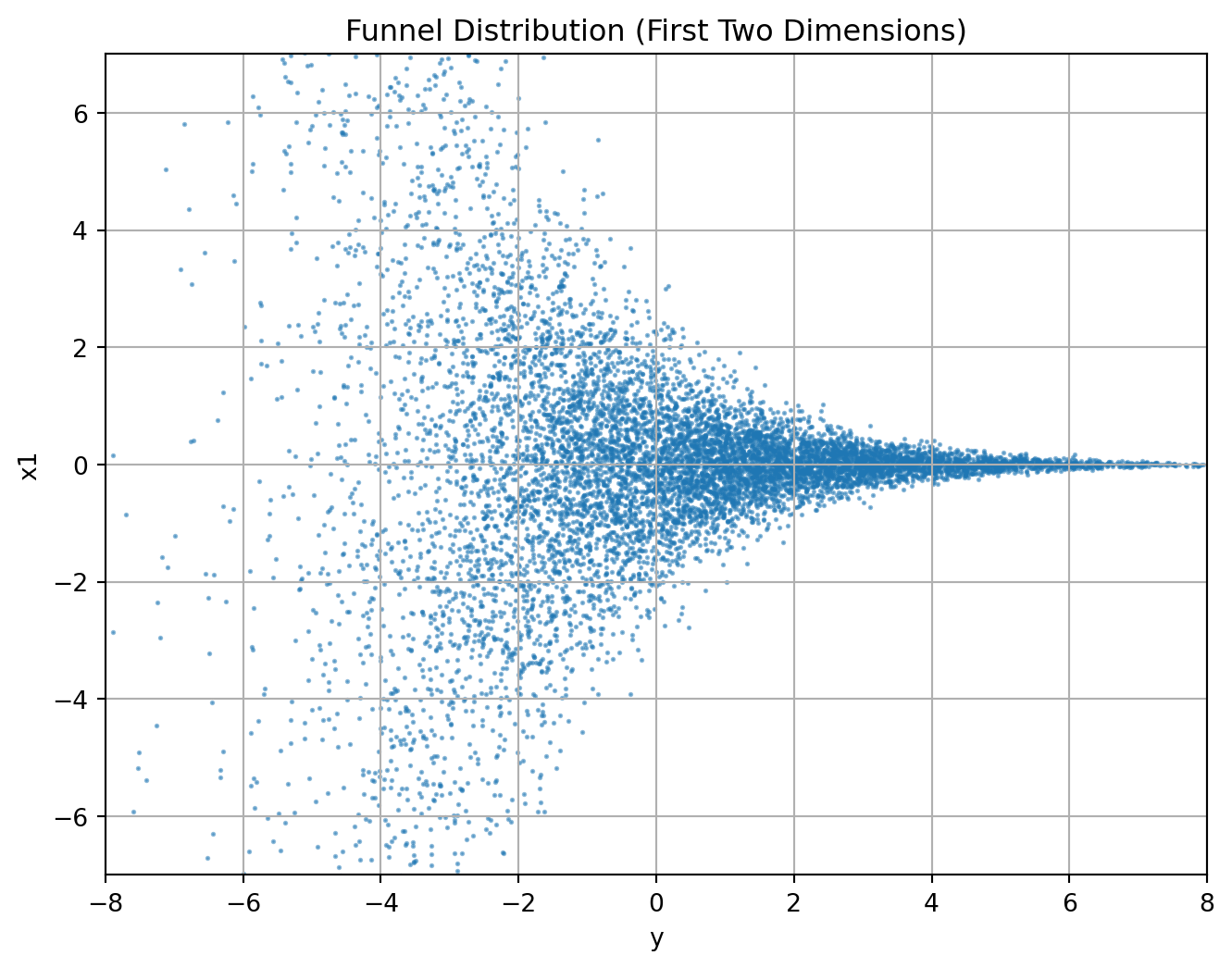

neg_energy, sample_data = funnel(d=2)

# y と x1 の範囲を設定
y_min, y_max = -9, 9
x1_min, x1_max = -8, 8
num_points = 1000  # グリッドの解像度

y_values = np.linspace(y_min, y_max, num_points)
x1_values = np.linspace(x1_min, x1_max, num_points)
Y, X1 = np.meshgrid(y_values, x1_values)

# グリッド上の点を作成
inputs = np.stack([Y.ravel(), X1.ravel()], axis=1)

# 対数密度を計算
log_density = neg_energy(inputs)
density = np.exp(log_density)

log_density = np.sqrt(density)

Density = log_density.reshape(Y.shape)

# 3Dプロットの作成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 軸のラベルを設定
ax.set_xlabel('y')
ax.set_ylabel('x1')
ax.set_zlabel('Density (Transformed)')

# サーフェスプロットを作成
surf = ax.plot_surface(Y, X1, Density, cmap='viridis', edgecolor='none')

# カラーバーを追加
fig.colorbar(surf, shrink=0.5, aspect=5)

# タイトルを設定
ax.set_title('Funnel Distribution Density on (x1,y)')

plt.show()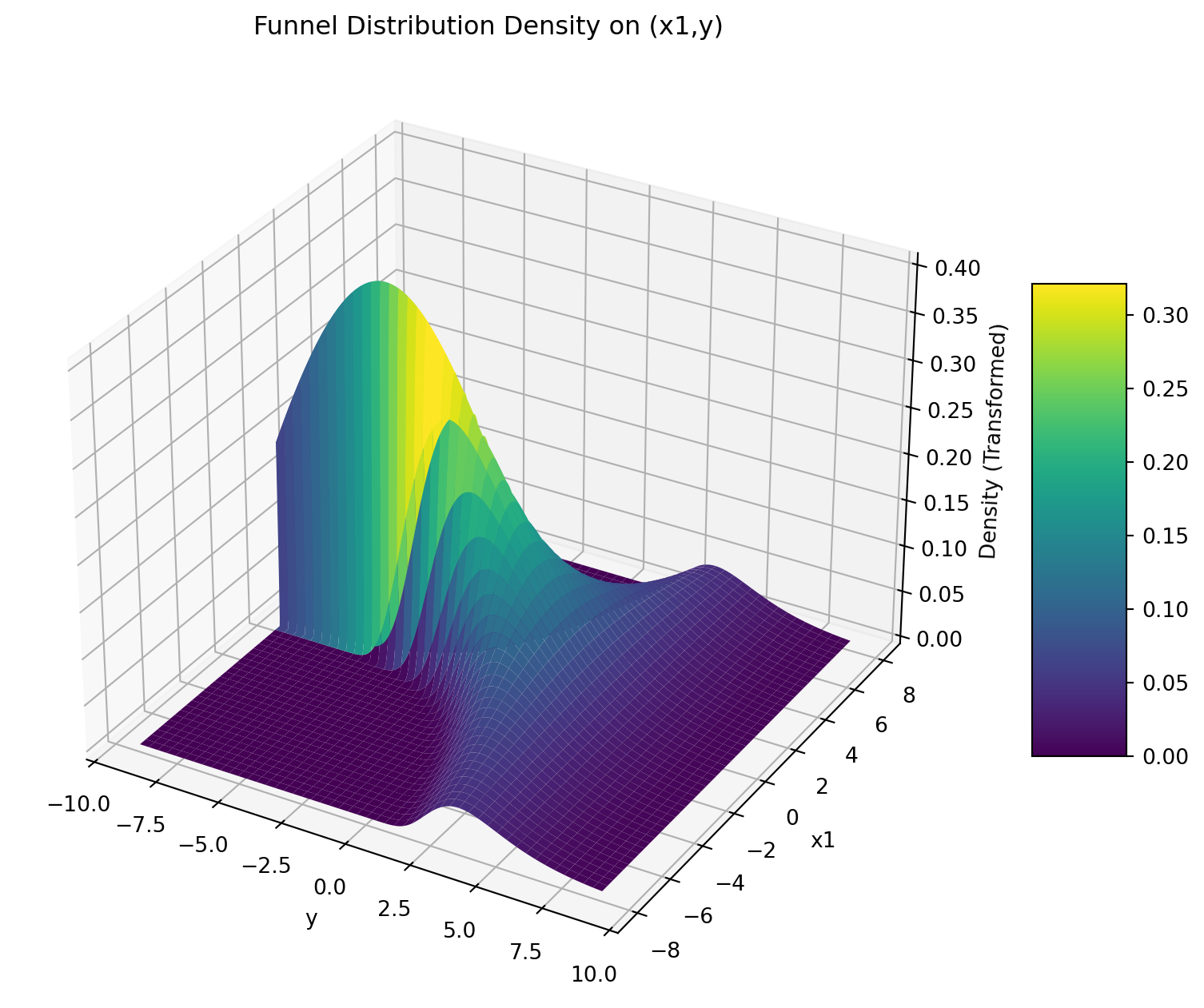

# 2Dヒートマップの作成
fig, ax = plt.subplots(figsize=(8, 6))

# pcolormeshを使用してヒートマップを作成
im = ax.pcolormesh(X1, Y, Density, cmap='binary', shading='auto')

# 軸のラベルを設定
ax.set_xlabel('x1')
ax.set_ylabel('y')

# カラーバーを追加
cbar = fig.colorbar(im, ax=ax, label='Density (Transformed)')

# タイトルを設定
ax.set_title('Funnel Distribution Density over y and x1')

plt.show()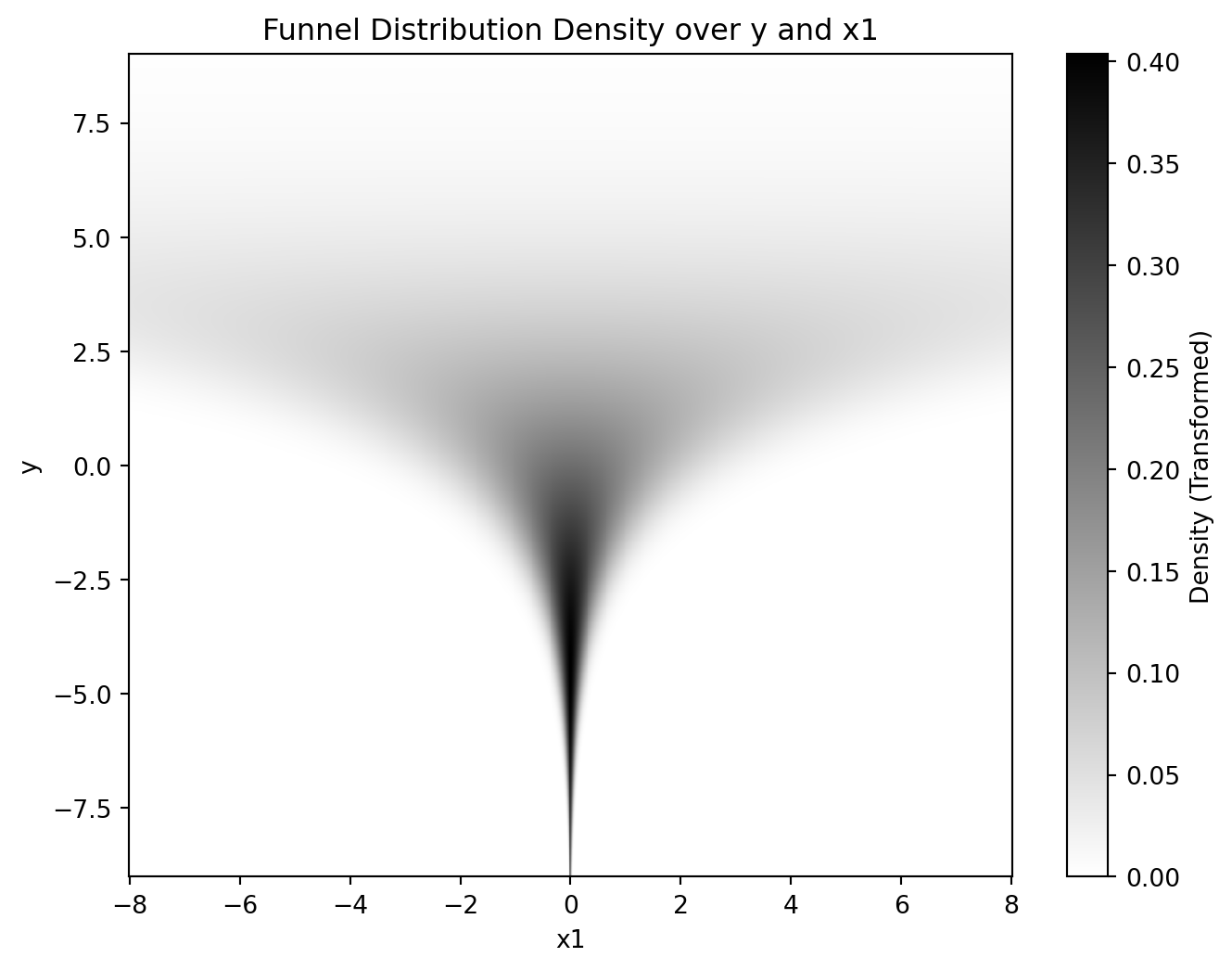

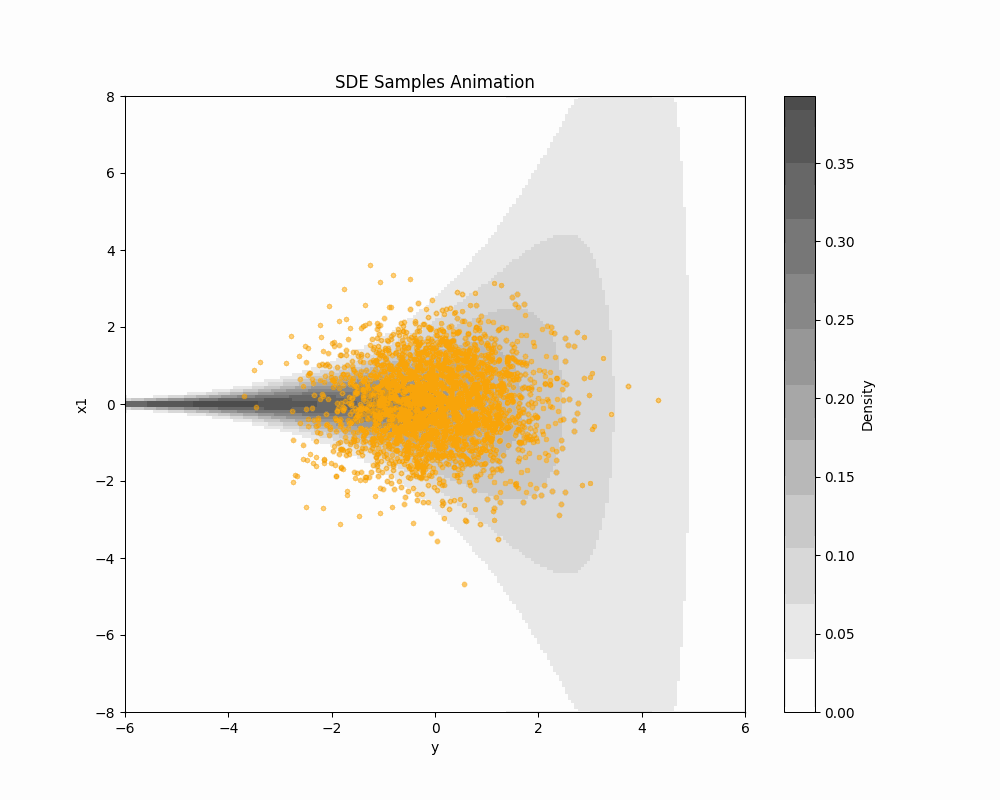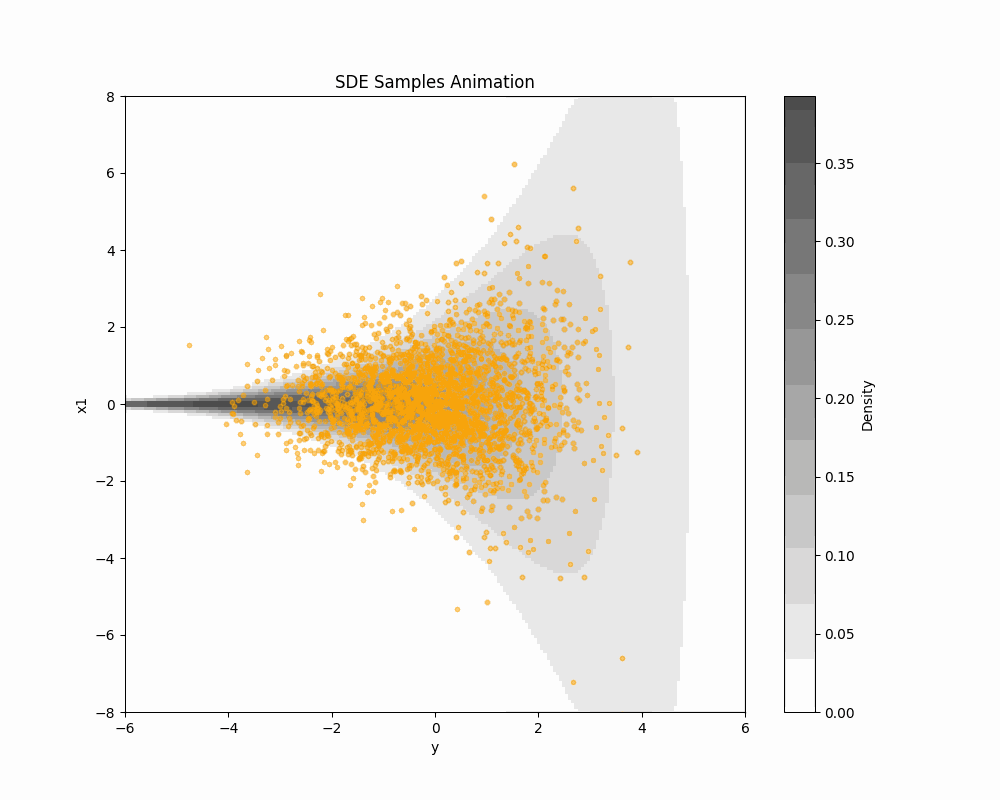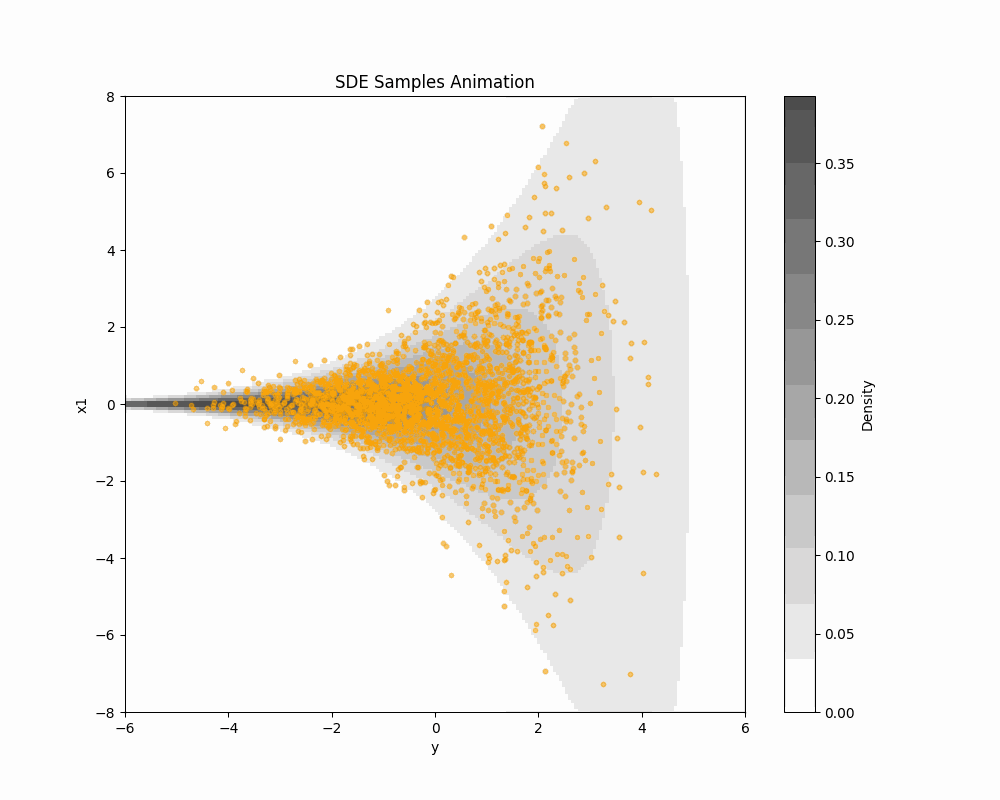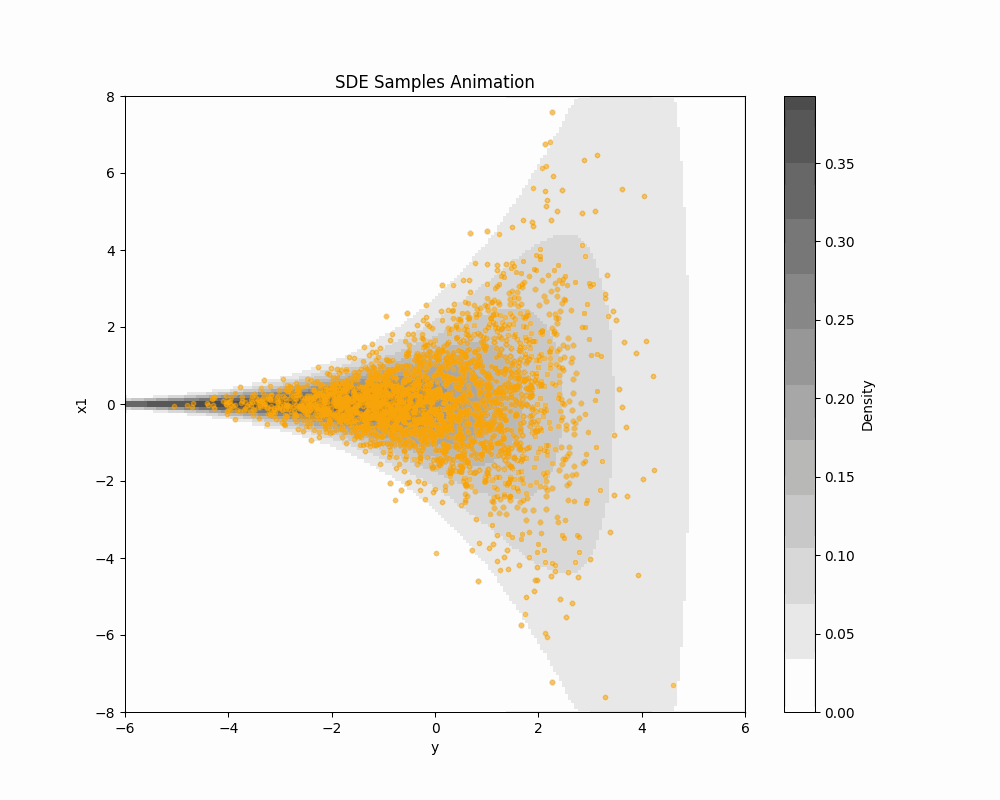
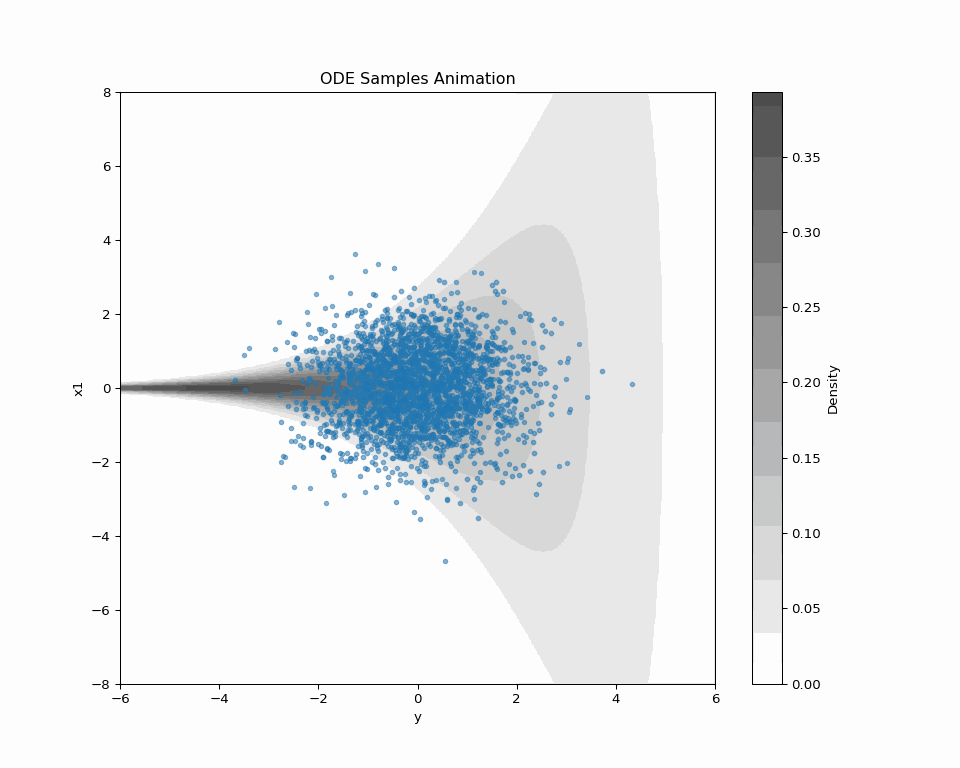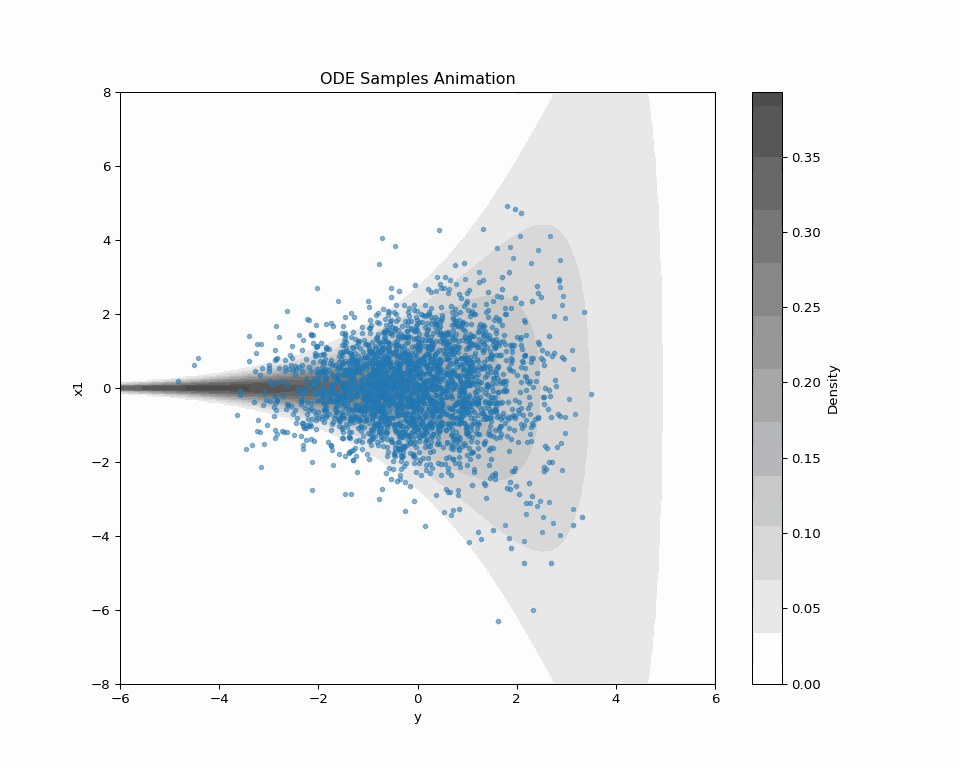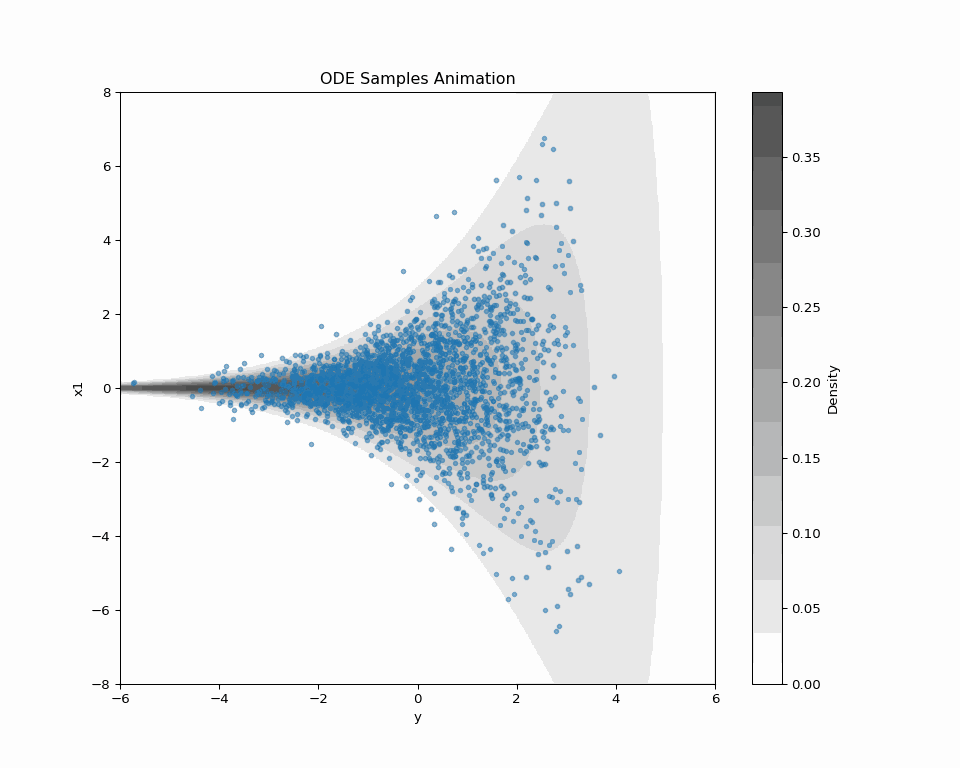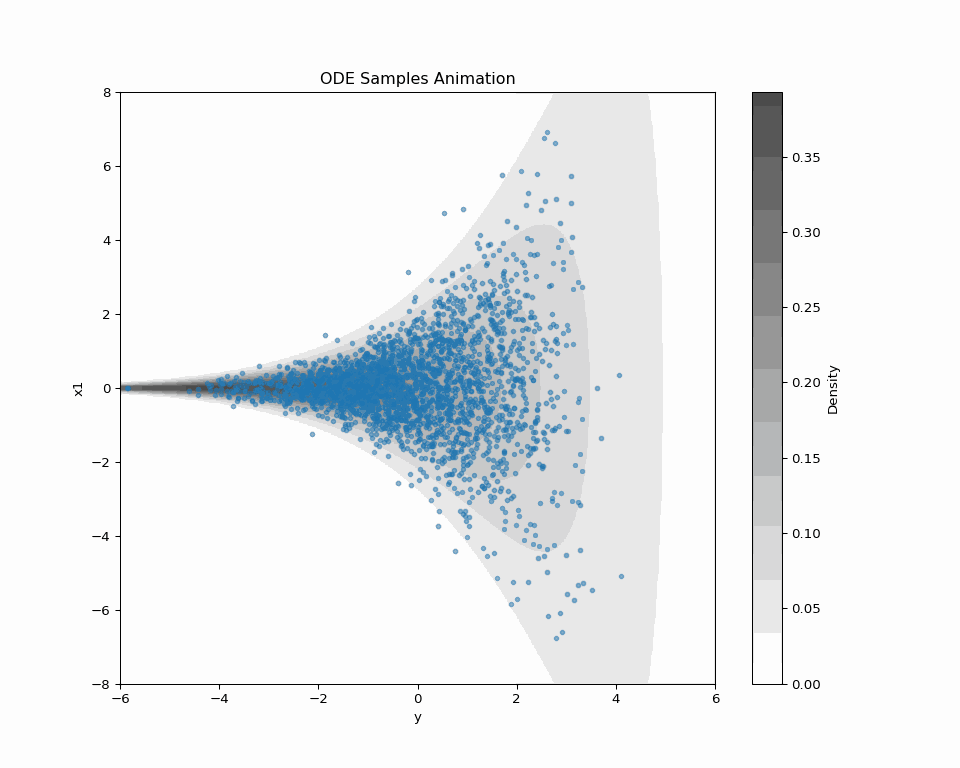
2 実験

DDS を Funnel 分布からのサンプリングに適用してみる．

実際の実験は こちらの Colab で行なった．

途中で WandB (Weights & Biases) を使う．

import numpy as np

sde_data = np.load('Files/sde_data.npy')
ode_data = np.load('Files/ode_data.npy')

import matplotlib.pyplot as plt

ode_targ = ode_data[:, -1,:2]
sde_targ = sde_data[:, -1,:2]

plt.plot(ode_targ[:, 0], ode_targ[:, 1], ".", alpha=0.4)
plt.plot(sde_targ[:, 0], sde_targ[:, 1], ".", alpha=0.4, color='orange')

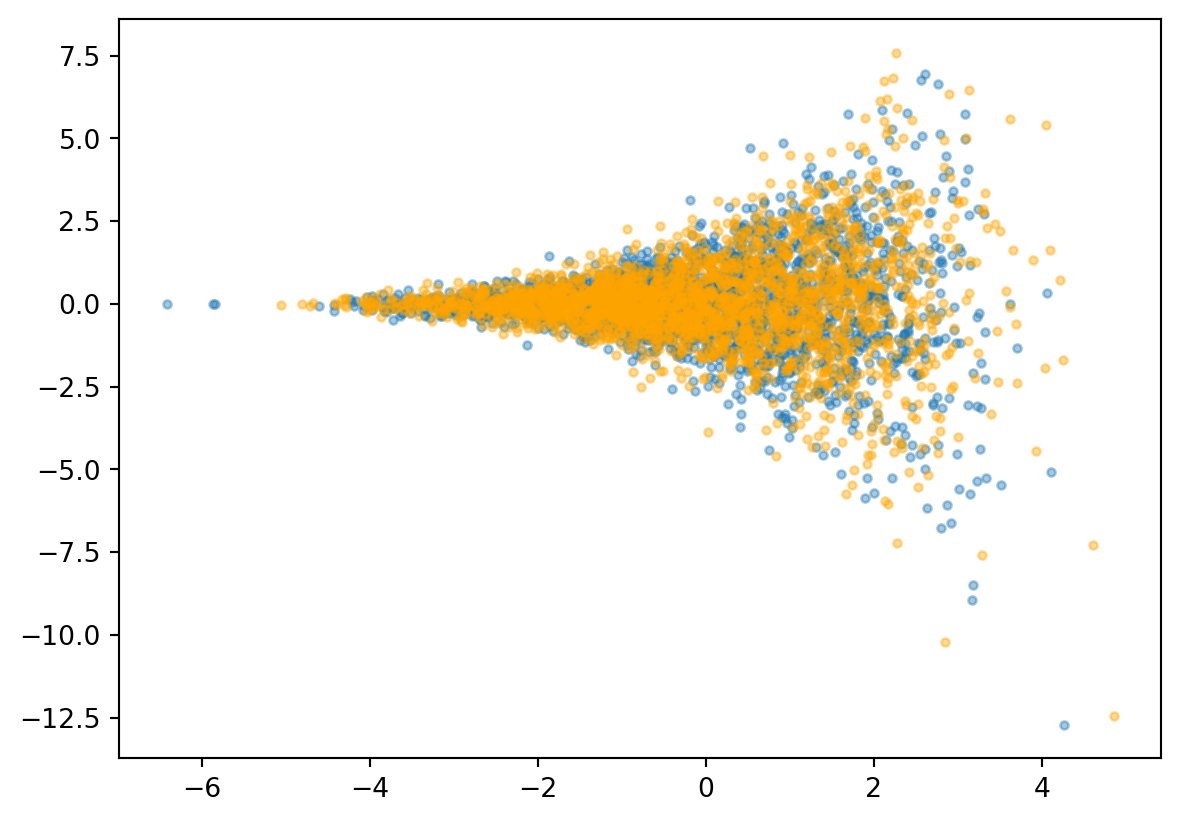
import matplotlib.animation as animation

# Density のヒートマップ作成（前述のコードから）
neg_energy, sample_data = funnel(d=2)

y_min, y_max = -6, 6
x1_min, x1_max = -8, 8
num_points = 200  # グリッドの解像度を下げて処理を軽くする

y_values = np.linspace(y_min, y_max, num_points)
x1_values = np.linspace(x1_min, x1_max, num_points)
Y, X1 = np.meshgrid(y_values, x1_values)

inputs = np.stack([Y.ravel(), X1.ravel()], axis=1)
log_density = neg_energy(inputs)
density = np.sqrt(np.exp(log_density))
Density = density.reshape(Y.shape)

# プロットの設定
fig, ax = plt.subplots(figsize=(10, 8))

# ヒートマップを描画（Density.T ではなく Density を使用）
im = ax.imshow(Density, extent=[y_min, y_max, x1_min, x1_max], 
               origin='lower', cmap='binary', aspect='auto', alpha=0.7)

# カラーバーを追加
plt.colorbar(im, label='Density')

# 初期データの取得
y0 = sde_data[:, 0, 0]  # y軸（第1次元）
x0 = sde_data[:, 0, 1]  # x軸（第2次元）
data0 = np.column_stack((y0, x0))

# 散布図を描画
scat = ax.scatter(data0[:, 0], data0[:, 1], s=10, alpha=0.5, color='orange')

# 軸の範囲を設定
ax.set_xlim(y_min, y_max)
ax.set_ylim(x1_min, x1_max)
ax.set_xlabel('y')
ax.set_ylabel('x1')
ax.set_title('SDE Samples Animation')

# 初期化関数
def init():
    scat.set_offsets(data0)
    return scat,

# フレームごとの更新関数
def animate(i):
    y = sde_data[:, i, 0]  # y軸（第1次元）
    x = sde_data[:, i, 1]  # x軸（第2次元）
    data = np.column_stack((y, x))
    scat.set_offsets(data)
    return scat,

# アニメーションの作成
ani = animation.FuncAnimation(
    fig, animate, init_func=init, frames=sde_data.shape[1],
    interval=50, blit=False)

# アニメーションの保存
ani.save('sde_animation.gif', writer='pillow', fps=20)

3 実装

Neal, R. M. (2003). Slice sampling. The Annals of Statistics, 31(3), 705–767.

Vargas, F., Grathwohl, W. S., and Doucet, A. (2023). Denoising Diffusion Samplers. In The eleventh international conference on learning representations.