雑音除去拡散サンプラー

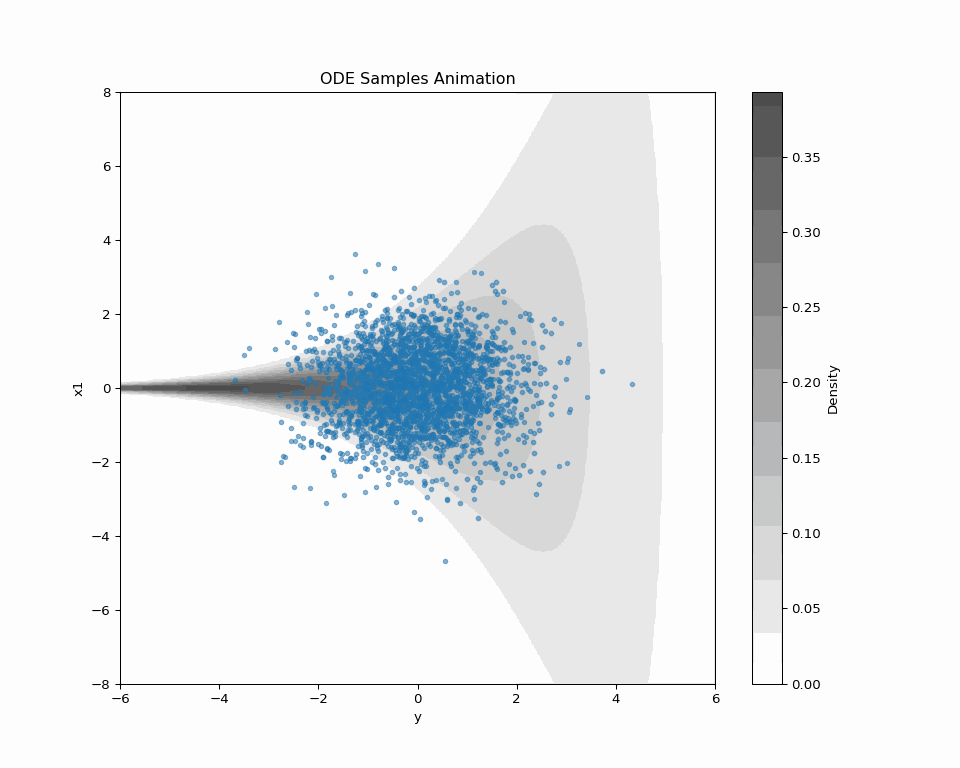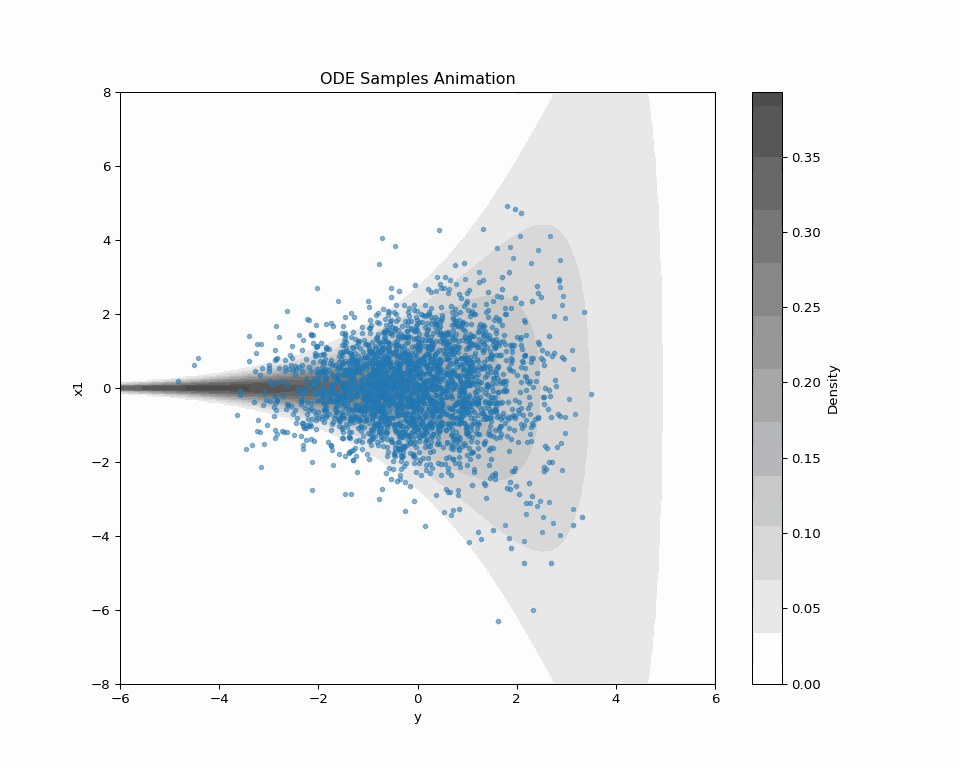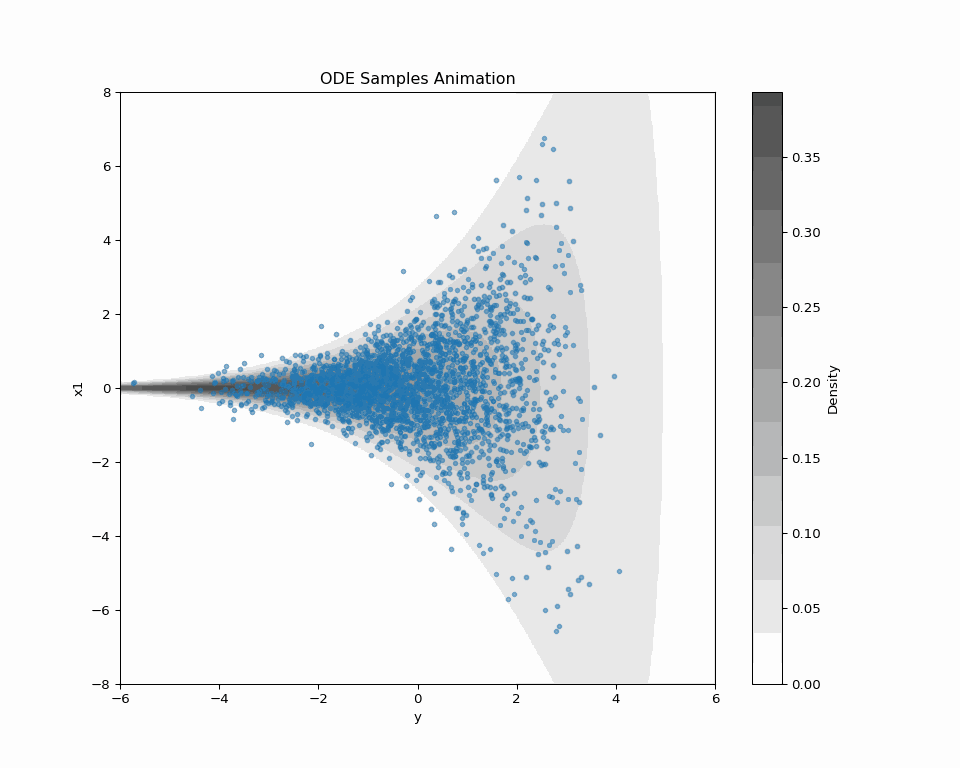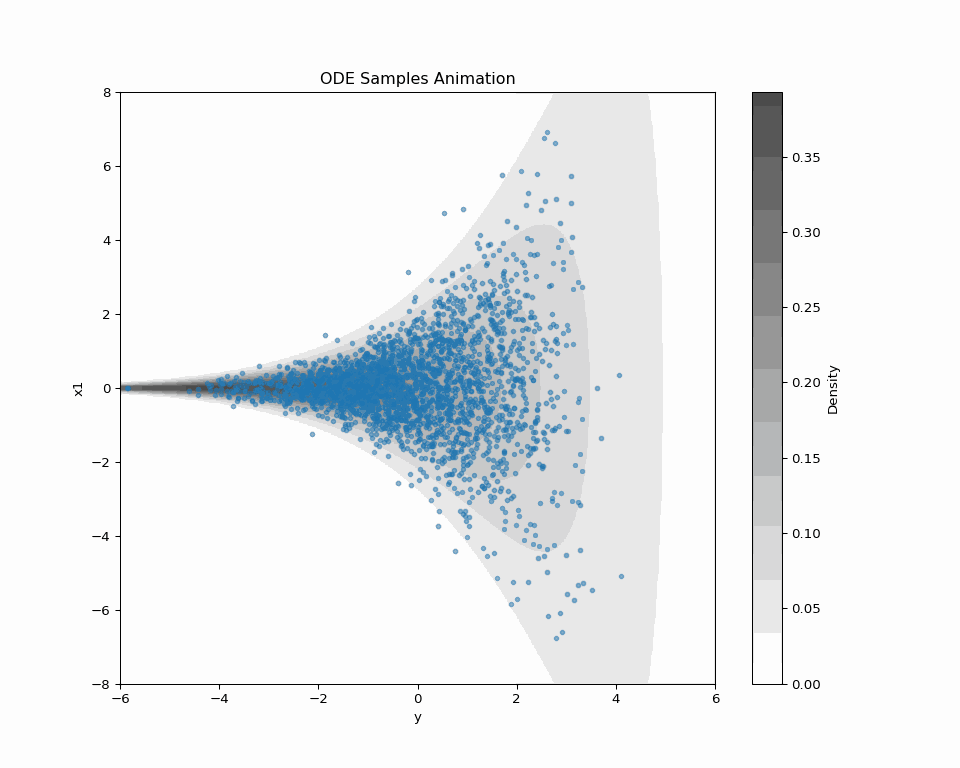
A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

関連ページ

1 雑音除去拡散によるサンプリング (DDGS)

1.1 はじめに

正規化定数が不明な分布 \[ p(x)=\frac{\gamma(x)}{Z},\qquad Z:=\int_\mathcal{X}\gamma(x)\,dx \] に対しても使える汎用サンプラーを考える．

DDPS では \(p(x|y)\,\propto\,g(y|x)p_0(x)\) の状況を考えており，\(p,g\) からのサンプルが必要であった．

特定の \(y\) に特化したモデリングというより償却推論であり，ベイズ事後分布からのサンプリングなどの設定では必ずしも良い性能を示さない（誘導 などの技術はある）．

(Vargas et al., 2023) は以上の２点を克服するサンプラーを提案した．まずは SB ではなく OU 過程を通じて議論し，次稿で SB を考える．

1.2 \(h\)-変換としての表示

雑音除去拡散 \[ dZ_t=\frac{1}{2}Z_t\,dt+\nabla_z\log p_{T-t}(Z_t|y)\,dt+dW_t,\qquad Z_0\sim p_T(x_T|y), \] とは \(p\) から始めた OU 過程 \[ dX_t=-\frac{1}{2}X_t\,dt+dB_t,\qquad X_0\sim p(x), \] の \([0,T]\) 上での時間反転なのであった．ドリフト項 \(\nabla_x\log p_t(x_t)\) をスコアマッチングにより学習することが不可能な設定であるため，この項が消えるような変数変換を考える．

まず，OU 過程 \((X_t)\) を定常分布 \(X_0\sim\operatorname{N}_d(0,I_d)\) から始めた場合の分布を \(\mathbb{M}\) とする．\(\mathbb{M}\) の時間反転 \((Z_t)\) は全く同様の表示を持つ： \[ dZ_t=-\frac{1}{2}Z_t\,dt+dW_t,\qquad Z_0\sim\operatorname{N}_d(0,I_d). \]

この過程の \(\mathbb{M}\) の下での \(h\)-変換は， \[ dZ_t=-\frac{1}{2}Z_t\,dt+\nabla_z\log h_{T-t}(Z_t)\,dt+dW_t,\qquad Z_0\sim p_T(x_T), \] \[ h_t(x_t):=\int_\mathcal{X}\Phi(x_0)m_{T|T-t}(x_0|x_t)\,dx_0,\qquad \Phi(x_0):=\frac{p(x_0)}{\phi_d(x_0;0,I_d)} \] と表せる．

ただし \(m\) は時間反転 \((Z_t)\) の遷移密度とした．

この表示に対するパラメトリックな近似 \[ dZ_t=-\frac{1}{2}Z_t\,dt+u^\theta_{T-t}(Z_t)\,dt+dW_t,\qquad Z_0\sim\operatorname{N}_d(0,I_d), \] の分布を \(\mathbb{Q}^\theta\) で表し，\(\operatorname{KL}(\mathbb{P},\mathbb{Q}^\theta)\) を最小化する，とすると雑音除去拡散の学習と全く同じことを繰り返している．\(\mathbb{P}\) からのサンプル，従って \(p\) からのサンプルを必要としてしまうので不適．

そこで，この逆 KL 乖離度を考える．

1.3 逆 KL-乖離度の最適制御

\(h\)-変換をした理由は，\(\operatorname{KL}(\mathbb{Q}^\theta,\mathbb{P})\) ならば計算できる点にある．

\[ \mathcal{L}(\theta):=\operatorname{KL}(\mathbb{Q}^\theta,\mathbb{P})=\operatorname{E}_{\mathbb{Q}^\theta}\left[\frac{1}{2}\int^T_0\|u^\theta_{T-t}(Z_t)\|^2\,dt-\log\Phi(Z_T)\right] \] については，\(\log\Phi(Z_T)\) には \(\theta\) が出現しないため，第一項のみに集中すれば良い．

そうすると，これは KL 最適制御問題として解くことができる．

これが DDGS (Vargas et al., 2023) である．

2 文献紹介

2.1 DDS の現状

MCMC, SMC そして ABC の代替手法ともくされているが，理論が未発達である．

例えば (Bortoli, 2022) などの既存の理論は，スコア関数の推定誤差の言葉で収束を論じており，この推定誤差は実践上では確認が難しいものであると言える (Heng et al., 2024)．

加えて，拡散模型は確率的局所化の考え方と関係が深いことが知られており，近似メッセージ伝搬を取り入れることで，定量的な収束保証をつけることもできる (Montanari and Wu, 2023)．

References

Bortoli, V. D. (2022). Convergence of denoising diffusion models under the manifold hypothesis. Transactions on Machine Learning Research.

Heng, J., Bortoli, V. D., and Doucet, A. (2024). Diffusion Schrödinger Bridges for Bayesian Computation. Statistical Science, 39(1), 90–99.

Montanari, A., and Wu, Y. (2023). Posterior sampling from the spiked models via diffusion processes.

Vargas, F., Grathwohl, W. S., and Doucet, A. (2023). Denoising Diffusion Samplers. In The eleventh international conference on learning representations.