Schrödinger 橋によるサンプリング

関連ページ

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

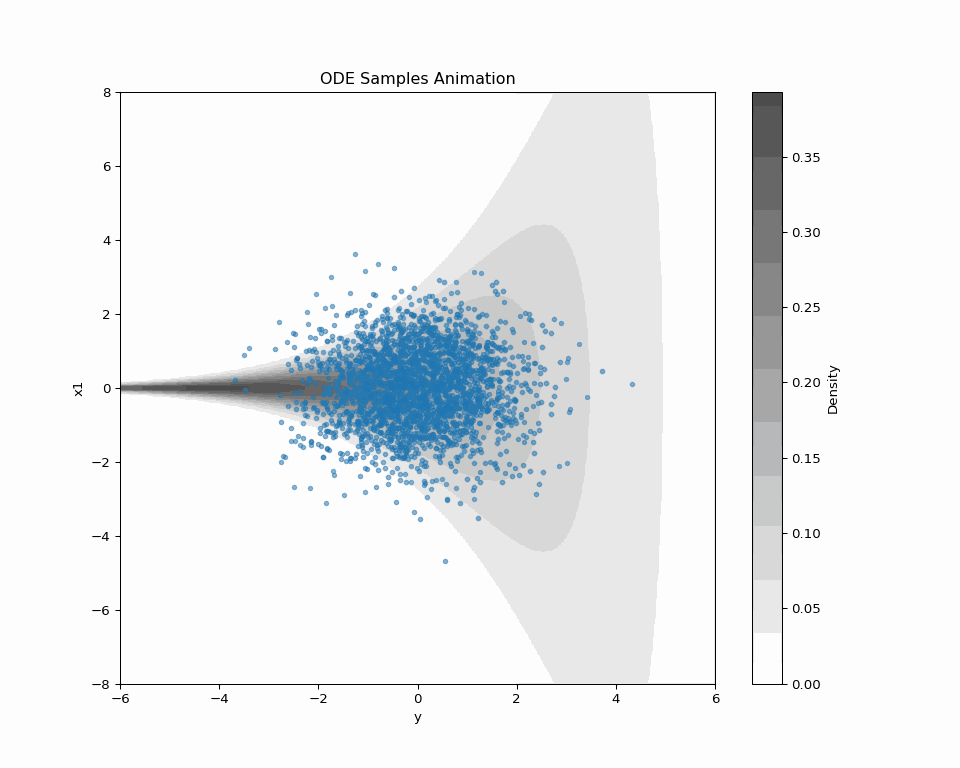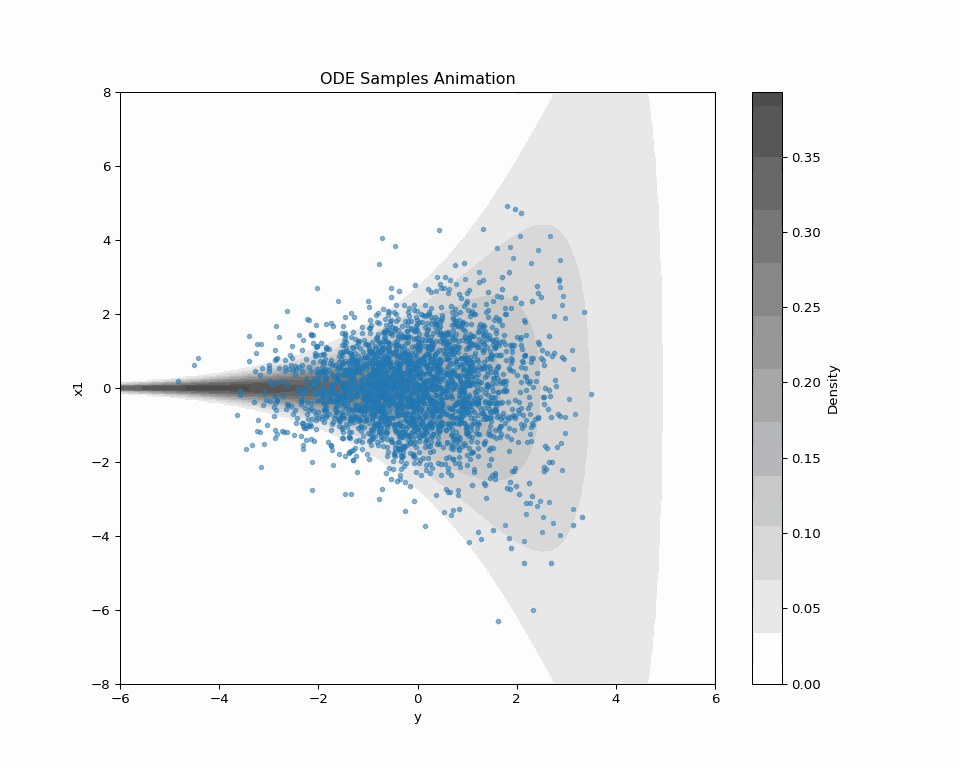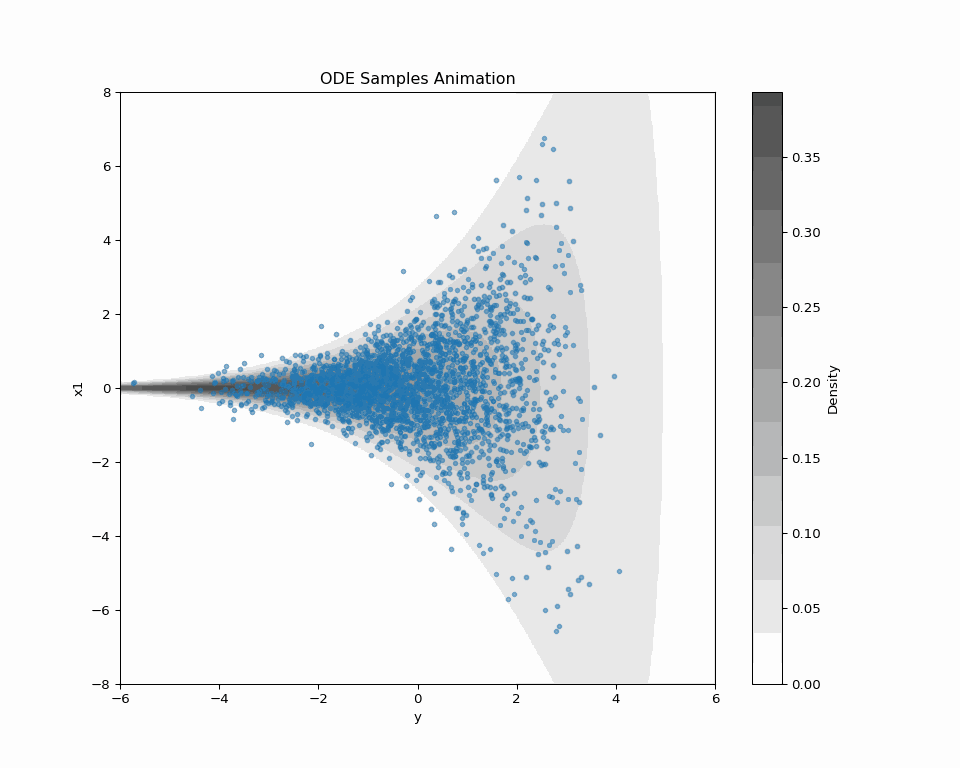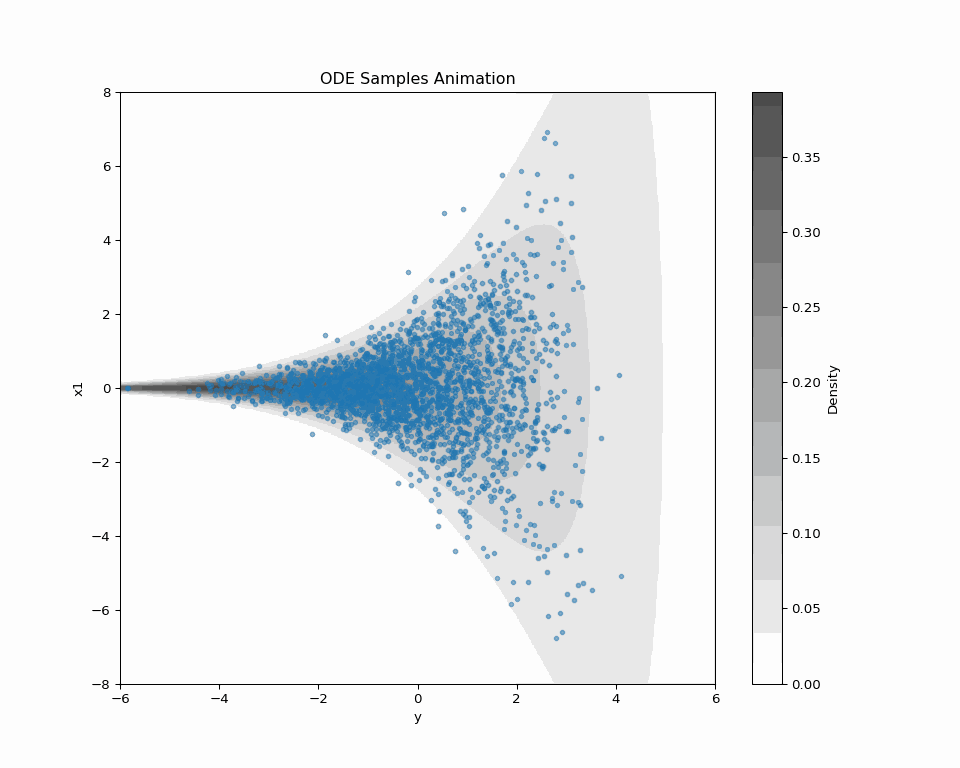
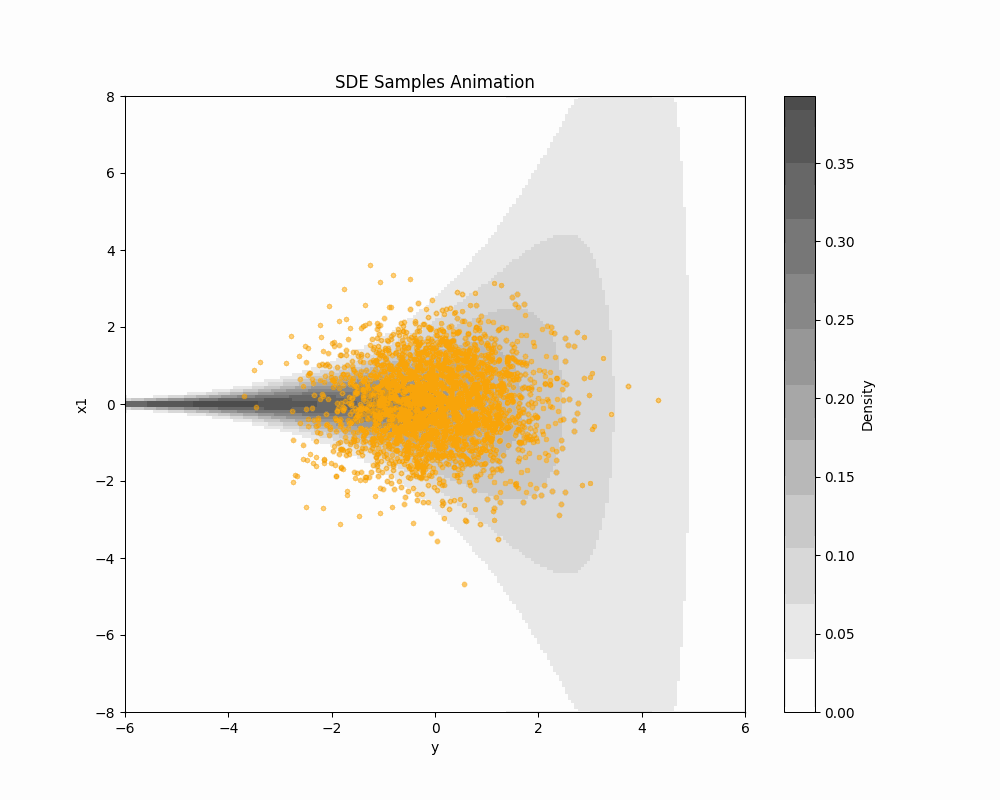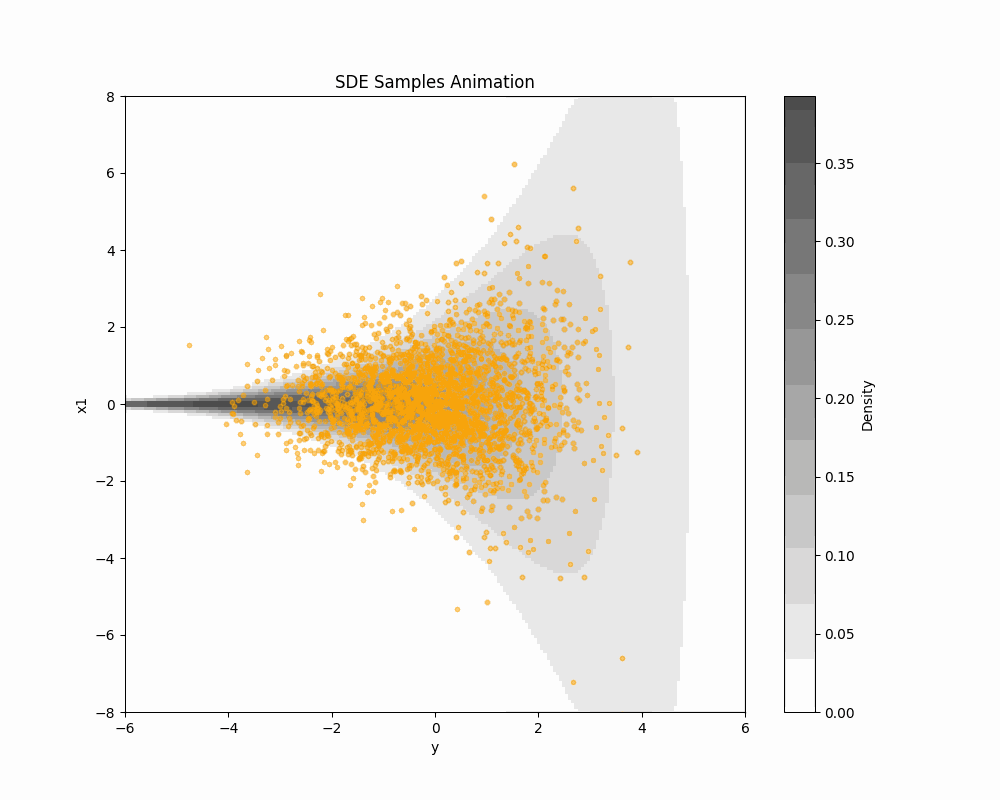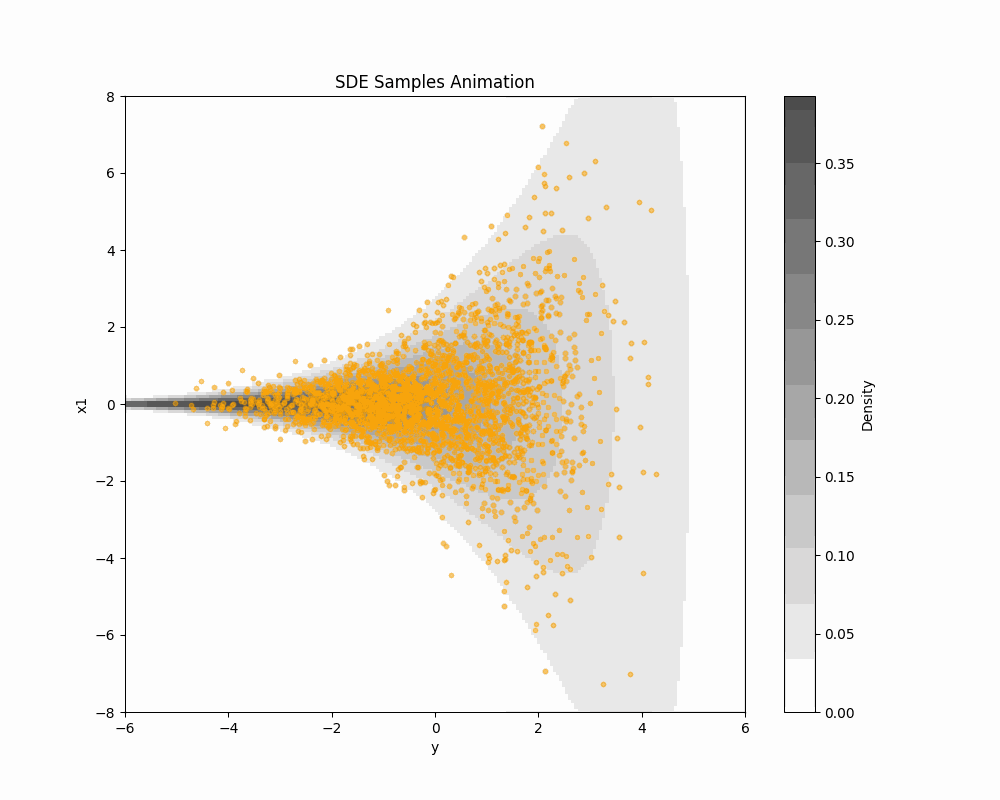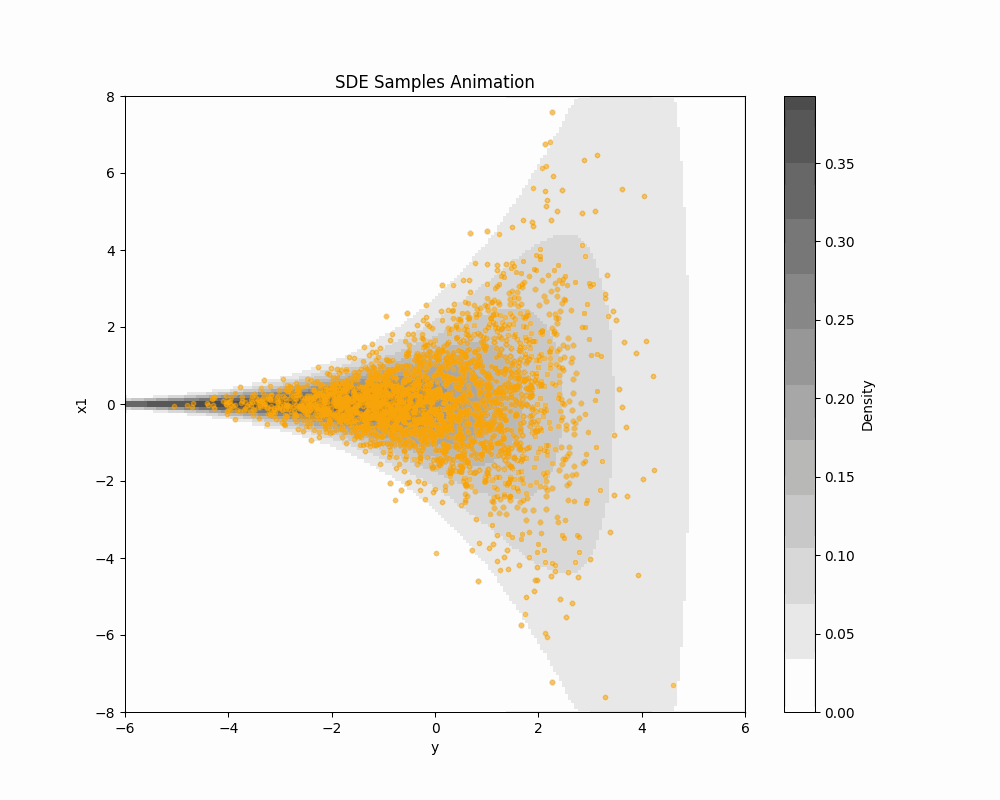
1 Schrödinger 橋によるサンプリング (DSB-GS)

1.1 はじめに

全く同様にして，Schrödinger 橋としての見方を導入することにより，DDGS の効率はさらに上げられる．

加えて，無雑音極限において，Schrödinger 橋問題は，エントロピー正則化を持つ最適輸送問題と Monge-Kantorovich 問題と関連がある (De Bortoli et al., 2021, p. 3.1節)．

この場合も，$T\to \mathrm{\infty }$ の極限において，DDGS は Schrödinger 橋の近似を与える．

1.2 Schrödiger-Föllmer サンプラー

$\mathbb{M}$ を OU 過程と取る代わりに，${\mathrm{\Pi }}_T(x_T)$ を Dirac 測度として Brown 橋を取ることもできる．これが (Föllmer, 1985) 以来のアプローチである．

このアプローチでは，IPF は２回のイテレーションで収束するという美点がある．このための数値的方法も広い分野で提案されている：(Barr et al., 2020), (Zhang et al., 2021)．

終端の測度を Dirac 測度としていることの綻びが数値的な不安定性に現れやすいことが (Vargas et al., 2023) で述べられている．

References

Barr, A., Gispen, W., and Lamacraft, A. (2020). Quantum ground states from reinforcement learning. In J. Lu and R. Ward, editors, Proceedings of the first mathematical and scientific machine learning conference,Vol. 107, pages 635–653. PMLR.

De Bortoli, V., Thornton, J., Heng, J., and Doucet, A. (2021). Diffusion schrödinger bridge with applications to score-based generative modeling. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems,Vol. 34, pages 17695–17709. Curran Associates, Inc.

Föllmer, H. (1985). An entropy approach to the time reversal of diffusion processes. In M. Metivier and E. Pardoux, editors, Stochastic differential systems filtering and control, pages 156–163. Berlin, Heidelberg: Springer Berlin Heidelberg.

Vargas, F., Grathwohl, W. S., and Doucet, A. (2023). Denoising Diffusion Samplers. In The eleventh international conference on learning representations.

Zhang, B., Sahai, T., and Marzouk, Y. (2021). Sampling via controlled stochastic dynamical systems. In I (still) can’t believe it’s not better! NeurIPS 2021 workshop.