変分推論１

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

より図が見やすい PDF 版は こちら．

関連ページ

1 導入

1.1 歴史

ハード \(K\)-平均法はモデルフリーのクラスタリングアルゴリズムである．Voronoi 分割による競争学習の一形態とも見れる．¹

一方で原論文 (Lloyd, 1982) では，パルス符号変調 の文脈で，アナログ信号の量子化の方法として提案している．²

実際，\(K\)-平均法は（非可逆）データ圧縮にも用いられる．クラスター中心での画像の値と，それ以外では帰属先のクラスター番号のみを保存すれば良いというのである．このようなアプローチを ベクトル量子化 (vector quantization) という．³

ソフト \(K\)-平均法とは，このようなデータ点のクラスターへの一意な割り当てを，ソフトマックス関数を用いて軟化したアルゴリズムであり，多少アルゴリズムとしての振る舞いは改善するとされている．

1.2 最適化アルゴリズムとしての見方

\(N\) 個のデータ \(\{x_n\}_{n=1}^N\) の \(K\) クラスへの \(K\)-平均クラスタリングアルゴリズムは，ハードとソフトの二種類存在するが，いずれも \[ J:=\sum_{n=1}^N\sum_{k=1}^Kr_{nk}\|x_n-\mu_k\|^2 \] という損失関数の逐次最小化アルゴリズムとみなせる．

この見方は，EM アルゴリズム への一般化の軸となる．

しかしこの目的関数 \(J\) が非凸関数であることが，第 5 節で示す実験結果で見る通り，アルゴリズムに強い初期値依存性をもたらす．

これをクラスタがより互いに離れるように，クラス割り当て法を修正することで対策した 最遠点クラスタリング (Gonzalez, 1985) が提案された．これは k-means++ (Arthur and Vassilvitskii, 2007) とも呼ばれており，データ圧縮法として用いた場合は復元誤差が \(O(\log K)\) でバウンド出来ることも示されている．

1.3 用いるデータ

実際のコードとデータを用いて \(K\)-平均法を解説する．

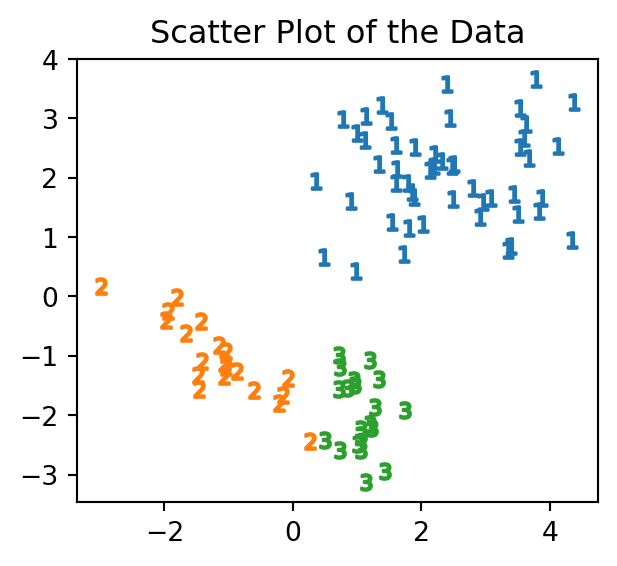
まずは，解説にために作られた，次のような３つのクラスタからなる２次元のデータを考え，これの正しいクラスタリングを目指す．

2 ハード \(K\)-平均法

2.1 アルゴリズムの説明

head \(K\)-means algorithm はデータ \(\{x^{(n)}\}_{n=1}^N\subset\mathbb{R}^I\) とクラスタ数 \(K\in\mathbb{N}^+\)，そして初期クラスター中心 \((m^{(k)})_{k=1}^K\in(\mathbb{R}^I)^K\) の３組をパラメータに持つ．

soft \(K\)-means algorithm 3.1 はさらに硬度パラメータ \(\beta\in\mathbb{R}_+\) を持つ．

numpy の提供する行列積を利用して，これを Python により実装した例を以下に示す．ソフト \(K\)-平均法の実装と対比できるように，負担率を通じた実装を意識した例である．

アノテーションを付してあるので，該当箇所（右端の丸囲み数字）をクリックすることで適宜解説が読めるようになっている．

def hkmeans_2d(data, K, init, max_iter=100):
    """
    ２次元データに対するハード K-平均法の実装例．

    Parameters:
    - data: (N,2)-numpy.ndarray
    - K: int クラスター数
    - init: (2,K)-numpy.ndarray 初期値

    Returns:
    - clusters: (N,)-numpy.ndarray クラスター番号
    """

    N = data.shape[0]
    I = data.shape[1]
    m = init
    r = np.zeros((K, N), dtype=float)

    for _ in range(max_iter):
        # Assignment Step
        for i in range(N):
            distances = np.array([d(data[i], m[:,k]) for k in range(K)])
            k_hat = np.argmin(distances)
            r[:,i] = 0
            r[k_hat,i] = 1
        
        # Update Step
        new_m = np.zeros_like(m, dtype=float)
        numerator = np.dot(r, data)
        denominator = np.sum(r, axis=1)
        for k in range(K):
            if denominator[k] > 0:
                new_m[:,k] = numerator[k] / denominator[k]
            else:
                new_m[:,k] = m[:,k]

        if np.allclose(m, new_m):
            break
        m = new_m
    
    return np.argmax(r, axis=0)

1

データ数を取得している．

2

データの次元を取得している．今回はすべて２次元データを用いる．

3

クラスター中心に引数として受け取った初期値を代入. \(2×K\)-行列であることに注意．

4

負担率を \(K×N\)-行列として格納している．その理由は後ほど行列積を通じた計算を行うためである．dtype=float の理由は後述．

5

この distances 変数は (K,)-numpy.ndarray になる．すなわち，第 \(k\) 成分が，第 \(k\) クラスター中心との距離となっているようなベクトルである．ただし，d は Euclid 距離を計算する関数として定義済みとした．

6

距離が最小となるクラスター番号 \(\hat{k}:=[\operatorname*{argmin}_{k\in[K]}d(m_k,x_i)]\) を，\(i\in[N]\) 番目のデータについて求める．

7

\(\hat{k}\) に基づいて負担率を更新するが，ループ内で前回の結果をリセットする必要があることに注意．

8

ここで dtype=float と指定しないと，初め引数 init が整数のみで構成されていた場合に，Python の自動型付機能が int 型だと判定し，クラスター中心 m の値が整数に限られてしまう．すると，アルゴリズムがすぐに手頃な格子点に収束してしまう．

9

numpy の行列積を計算する関数 np.dot を使用している．更新式 \[ m^{(k)}\gets\frac{\sum_{n=1}^Nr^{(n)}_kx^{(n)}}{\sum_{n=1}^Nr^{(n)}_k} \] の分子を行列積と見たのである．

10

分母 (denominator) は \((K,N)\)-行列 r の行和として得られる．

11

ゼロによる除算が起こらないように場合わけをしている．

12

クラスター中心がもはや変わらない場合はアルゴリズムを終了する．

13

負担率の最も大きいクラスター番号を返す．今回は hat_k の列をそのまま返せば良いが，soft \(K\)-means アルゴリズムにも通じる形で実装した．

注：実際に用いる実装

ただし，本記事の背後では次の実装を用いる．

クラスター中心の推移のヒストリーを保存して図示に利用したり，負担率 r の中身を見たりすることが出来るようにするため，assignment step と update step とに分けてクラスメソッドとして実装し，run メソッドでそれらを呼び出すようにしている．これに fetch_cluster と fetch_history メソッドを加えることで，クラスター番号とクラスター中心の推移を取得することが出来る．フィールド .r から（最終的な）負担率を見ることもできる．

class kmeans_2d:
    """
    ２次元データに対するソフト K-平均法の実装．

    Usage:
        kmeans = kmeans_2d(data, K, init, beta)
        kmeans.run()

    Parameters:
    - data: (N,2)-numpy.ndarray
    - K: int クラスター数
    - init: (2,K)-numpy.ndarray 初期値
    - beta: float 硬度パラメータ
    """

    def __init__(self, data, K, init, beta, max_iter=100):
        self.data = np.array(data, dtype=float)
        self.K = K
        self.init = np.array(init, dtype=float)
        self.beta = float(beta)
        self.max_iter = max_iter
        self.N = data.shape[0]  # データ数
        self.I = data.shape[1]  # 次元数 今回は２
        self.m = init  # クラスター中心の初期化．2×K行列．
        self.r = np.zeros((K, self.N), dtype=float)  # 負担率．K×N行列．
        self.history = [init.copy()] # クラスター中心の履歴．2×K行列．
    
    def soft_assigment(self):
        """soft K-means の場合の負担率の更新"""
        for i in range(self.N):
            distances = np.array([d(self.data[i], self.m[:,j]) ** 2 for j in range(self.K)]) # (N,)-numpy.ndarray
            denominator_ = np.sum(np.exp(-self.beta * distances))  # 分母
            self.r[:,i] = np.exp(- self.beta * distances) / denominator_

    def hard_assigment(self):
        """hard K-means の場合の負担率の更新"""
        for i in range(self.N):
            distances = np.array([d(self.data[i], self.m[:,j]) for j in range(self.K)]) # (N,)-numpy.ndarray
            k_hat = np.argmin(distances)  # 最小距離のクラスター番号
            self.r[:,i] = 0  # 前のループの結果をリセット
            self.r[k_hat,i] = 1
    
    def update(self):
        """クラスター中心の更新"""
        new_m = np.zeros_like(self.m, dtype=float) # ここで float にしないと，クラスター中心が整数に限られてしまう．
        numerator = np.dot(self.r, self.data)  # (K,2)-numpy.ndarray
        denominator = np.sum(self.r, axis=1)  # 各クラスターの負担率の和
        for k in range(self.K):
            if denominator[k] > 0:
                new_m[:,k] = numerator[k] / denominator[k]
            else:
                new_m[:,k] = self.m[:,k]
        self.m = new_m

    def fetch_cluster(self):
        """最終的なクラスター番号を格納した (N,)-array を返す"""
        return np.argmax(self.r, axis=0)
    
    def fetch_history(self):
        """クラスター中心の履歴を格納したリストを，３次元の np.array に変換して返す"""
        return np.stack(self.history, axis=0)

    def run_soft(self):
        """soft K-means アルゴリズムの実行"""
        for _ in range(self.max_iter):
            self.soft_assigment()
            self.update()
            self.history.append(self.m.copy())
            if np.allclose(self.history[-1], self.history[-2]):
                break
    
    def run_hard(self):
        """hard K-means アルゴリズムの実行"""
        for _ in range(self.max_iter):
            self.hard_assigment()
            self.update()
            self.history.append(self.m.copy())
            if np.allclose(self.history[-1], self.history[-2]):
                break

なお，この実装は \(\beta\ge500\) などの場合にオーバーフローが起こることに注意．これへの対処は logsumexp の使用などが考えられる．

2.2 初期値依存性

次の２つの初期値を与えてみる． \[ m_1:=\begin{pmatrix}4\\0\end{pmatrix},\quad m_2:=\begin{pmatrix}1\\4\end{pmatrix},\quad m_3=\begin{pmatrix}-1\\1\end{pmatrix}, \] と，\(m_2,m_3\) は変えずに \(m_1\) の \(y\)-座標を \(1\) だけ下げたもの \[ m_1':=\begin{pmatrix}4\\-1\end{pmatrix} \] とを初期値として与えてみる．

図 1: ハード K-平均法によるクラスタリングの結果．初期値は \((m_1,m_2,m_3)=\left(\begin{pmatrix}4\\0\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．赤丸で囲まれている点がクラスター中心 (CoC / Center of Cluster) の初期値で，その後の移動が図示されている．

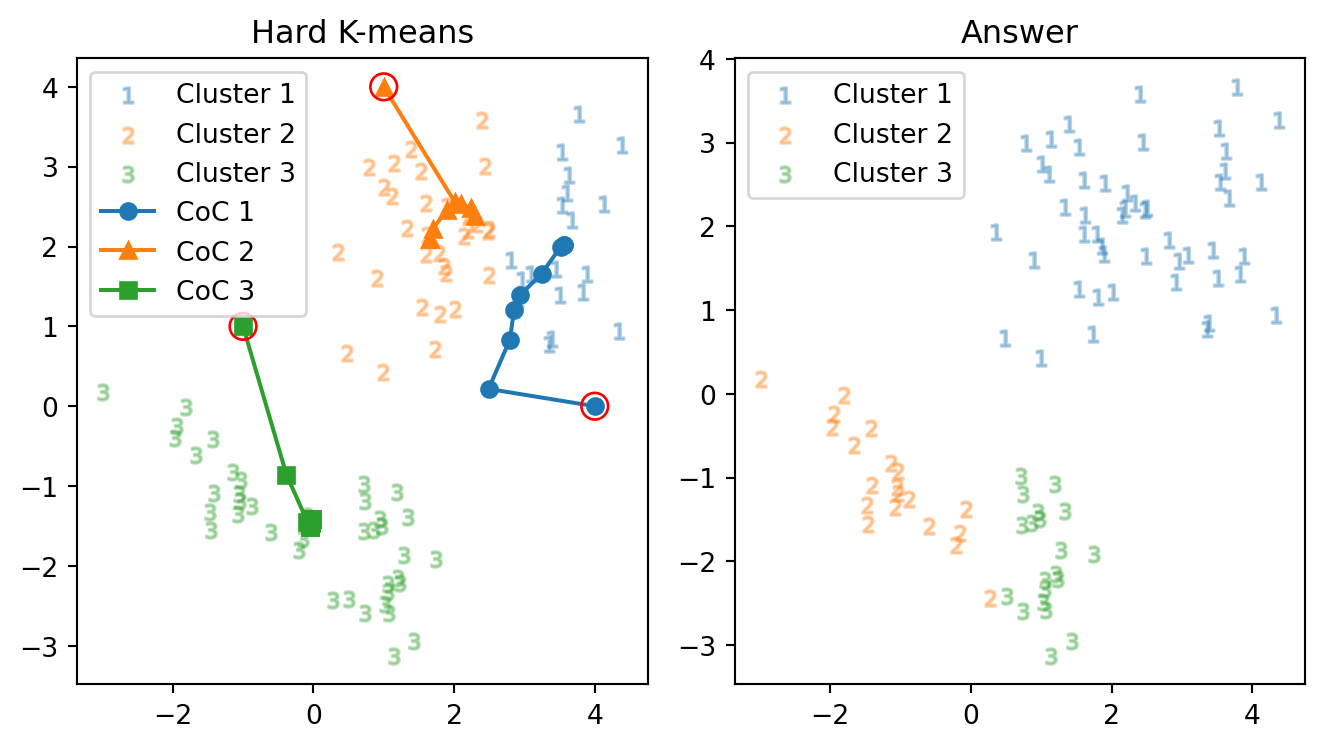
正解数: 51     正解率: 56.7 %     反復数: 9 回

別の初期値を与えてみる（右下の点 \(m_1\) を \(1\) だけ下に下げただけ）： \[ \begin{pmatrix}4\\0\end{pmatrix}=m_1\mapsto m_1':=\begin{pmatrix}4\\-1\end{pmatrix} \]

図 2: ハード K-平均法によるクラスタリングの結果．初期値は \((m_1',m_2,m_3)=\left(\begin{pmatrix}4\\-1\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．

正解数: 85     正解率: 94.4 %     反復数: 7 回

結果が全く変わり，\((m_1',m_2,m_3)\) を与えた方が，大きく正解に近づいている．具体的には，右下の初期値 \(m_1\) は右上の島に行くが，\(m_1'\) は左下の島に行ってくれる．

ハード \(K\)-平均アルゴリズムは初期値に敏感である ことがよく分かる．

2.3 局所解への収束

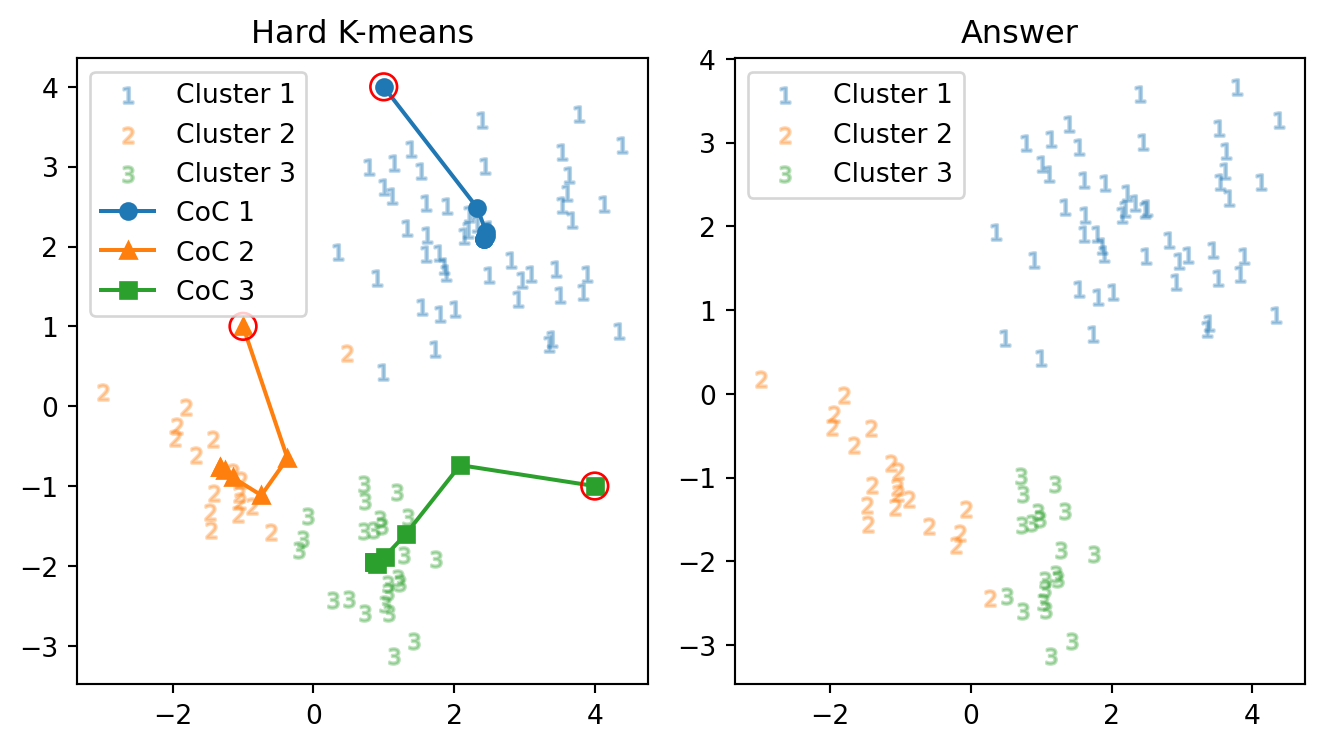
直前の結果2ではクラスター２と３の境界線で４つのミスを犯しており，これを修正できないか試したい．

そこで，答えに近いように， \[ m_1\gets\begin{pmatrix}2.5\\2\end{pmatrix},\;\; m_2\gets\begin{pmatrix}-1\\-1\end{pmatrix},\;\; m_3\gets\begin{pmatrix}1\\-2\end{pmatrix}, \] を初期値として与えてみて，正答率の変化を観察する．

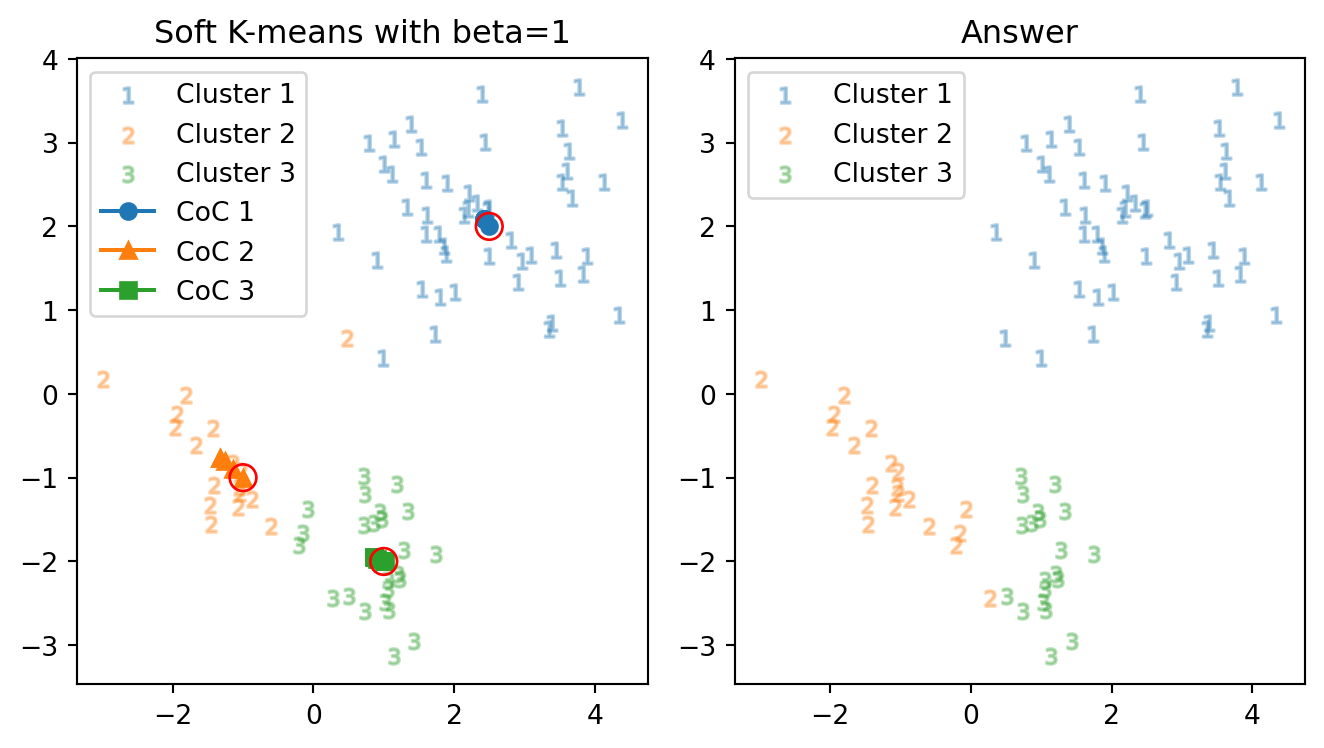
正解数: 85     正解率: 94.4 %     反復数: 5 回

もはや初期値から殆ど動いていないが，目標のクラスター３に分類された３つの点が，相変わらず３のままであり，加えてクラスター２の中心がこれらから逃げているようにも見えるので，クラスター２の初期値をよりクラスター３に近いように誘導し，クラスター３の中心をより右側から開始する：

\[ m_2:\begin{pmatrix}-1\\-1\end{pmatrix}\mapsto\begin{pmatrix}0\\-2\end{pmatrix}\;\; m_3:\begin{pmatrix}1\\-2\end{pmatrix}\mapsto\begin{pmatrix}2\\-2\end{pmatrix} \]

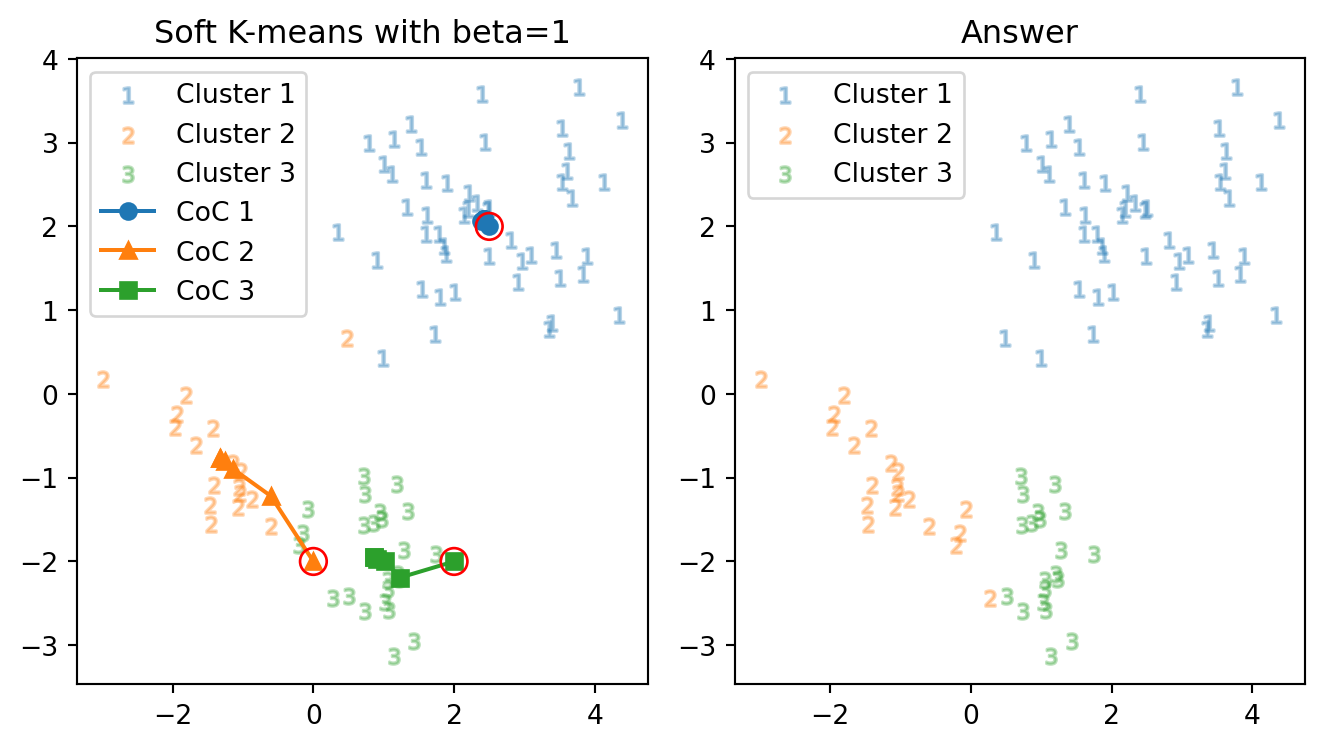
正解数: 85     正解率: 94.4 %     反復数: 6 回

こんなに誘導をしても，正しく分類してくれない．

実は，以上２つの初期値では，最終的に３つのクラスター中心は同じ値に収束している．よって，これ以上どのように初期値を変更しても，正答率は上がらないシナリオが考えられる．

以上の観察から，ハード \(K\)-平均法はある種の 局所解に収束する ようなアルゴリズムであると考えられる．

3 ソフト \(K\)-平均法

3.1 アルゴリズムの説明

ハード \(K\)-平均法2では，負担率 \[ r_{kn}\gets\delta_{k}(\operatorname*{argmax}_{i\in[k]}d(m_i,x_n)) \] は \(0,1\) のいずれかの値しか取らなかった．この振る舞いを， \[ \sigma(z;e)_i:=\frac{e^{z_i}}{\sum_{j=1}^Ke^{e_j}}\quad(i\in[K]) \] で定まる ソフトマックス関数 \(\sigma:\mathbb{R}^K\to(0,1)^K\) を用いて，「軟化」する．

ここでは，\(\beta\ge0\) として， \[ \sigma(z;e^{-\beta})_i=\frac{e^{-\beta z_i}}{\sum_{j=1}^Ke^{-\beta e_j}} \] の形で用い，\(\operatorname*{argmax}\) の代わりに \[ \begin{align*} r_{kn}&\gets\sigma(d(-,x_n)^2\circ m;e^{-\beta})_k\\ &=\frac{e^{-\beta d(m_k,x_n)^2}}{\sum_{j=1}^K e^{-\beta d(m_j,x_n)^2}} \end{align*} \] とする．ただし，\(d\) は \(\mathbb{R}^2\) 上の Euclid 距離とした．

3.1.1 硬度パラメータ

\(\beta\) は 硬度 (stiffness) または逆温度と呼ぶ．⁴ \(\sigma:=\beta^{-1/2}\) は距離の次元を持つ．

\(\beta=0\) のときは温度が無限大の場合にあたり，常に負担率は一様になる．絶対零度に当たる \(\beta\to\infty\) の極限が hard \(K\)-means アルゴリズムに相当する．

逆温度 \(\beta\) を連続的に変化させることで，クラスタ数に分岐が起こる，ある種の相転移現象を見ることができる．⁵

3.1.2 実装

実装は例えば hard \(K\)-means アルゴリズム2から，負担率計算の部分のみを変更すれば良い：

for i in range(N):
        distances = np.array([d(data[i], m[:,k]) for k in range(K)])
        denominator_ = np.sum(np.exp(-beta * distances))
        r[:,i] = np.exp(-beta * distances) / denominator_

1

データ \(x_i\) とクラスター中心 \((m_k)_{k=1}^K\) との距離を計算し，ベクトル \((d(x_n,m_k))_{k=1}^K\) を distances に格納している．

2

負担率の計算 \[ r_{ik}=\frac{\exp(-\beta d(m_k,x_i))}{\sum_{j=1}^K\exp(-\beta d(m_j,x_i))} \] を２段階に分けて行なっており，分母を先に計算して変数 denominator_ に格納している．

3

すでに計算してある分母 denominator_ を用いてデータ \(x_i\) の負担率 \((r_{ki})_{k=1}^K\) を計算し，\((K,N)\)-行列 r の各列に格納している．

3.2 挙動の変化の観察

逆温度をはじめに \(\beta=0.3\) としてみる．図 1 と全く同様な初期値 \[ m_1:=\begin{pmatrix}4\\0\end{pmatrix},\quad m_2:=\begin{pmatrix}1\\4\end{pmatrix},\quad m_3=\begin{pmatrix}-1\\1\end{pmatrix}, \] を与えてみると，次の通りの結果を得る：

図 3: 左がソフト K-平均法（\(\beta=1\)），右がハード K-平均法によるクラスタリングの結果（図２の左と全く同じもの）．初期値は \((m_1,m_2,m_3)=\left(\begin{pmatrix}4\\0\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．赤丸で囲まれている点がクラスター中心 (CoC / Center of Cluster) の初期値で，その後の移動が図示されている．

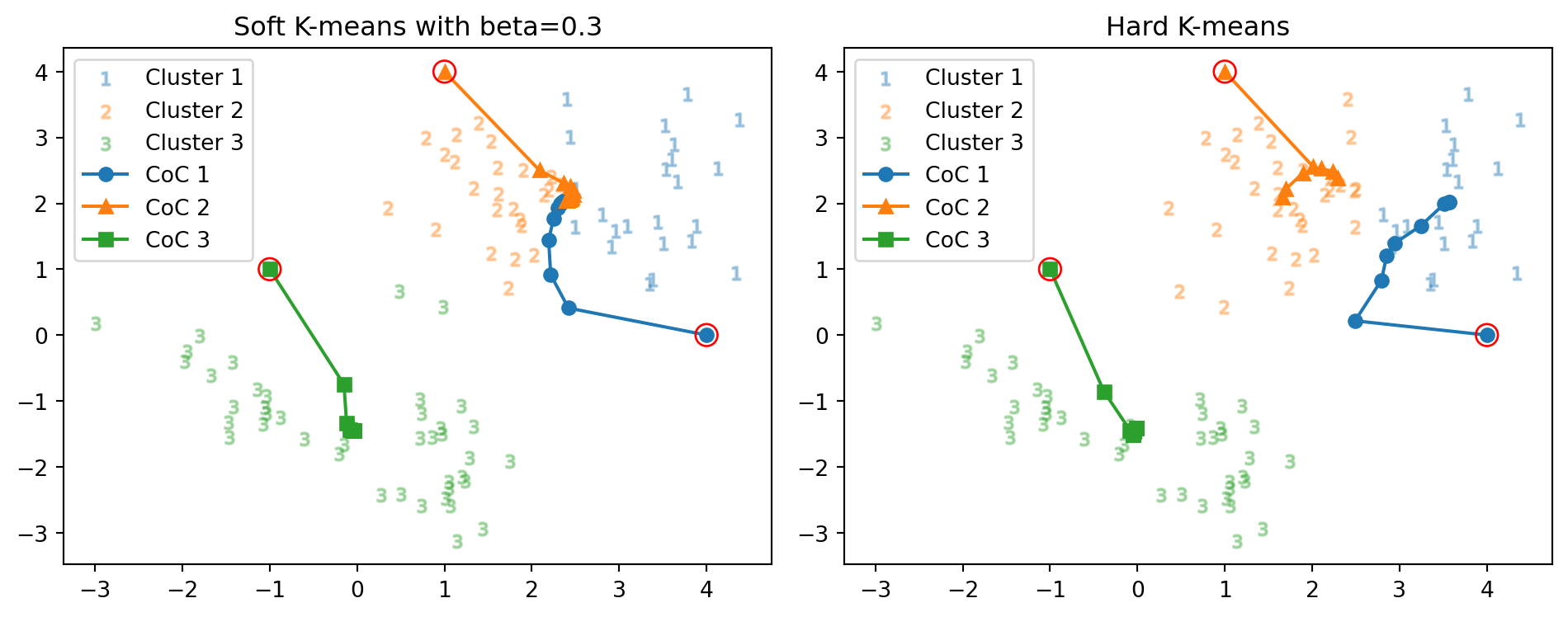
正解数: 44 vs. 51     正解率: 48.9 % vs. 56.7 %     反復数: 28 回 vs. 9 回

クラスターの境界が変化しており，正解率は悪化している．さらに，反復数が９回であったところから，３倍に増えている（28回）．

また，右上の２つのクラスター中心の収束先は，微妙にずれているが ほとんど一致している 点も注目に値する．

参考：最終的なクラスター中心の座標

centers = history[-1, :, :]
df = pd.DataFrame(centers, columns=['Cluster1', 'Cluster2', 'Cluster3'])
print(df)

   Cluster1  Cluster2  Cluster3
x  2.397456  2.397535 -0.036071
y  2.047565  2.047580 -1.448288

図 2 で与えた初期値 \((m_1',m_2,m_3)\) も与えてみる．

図 4: ソフト K-平均法（\(\beta=1\)）によるクラスタリングの結果，右がハード K-平均法によるクラスタリングの結果（図２の右と全く同じもの）．初期値は \((m_1',m_2,m_3)=\left(\begin{pmatrix}4\\-1\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．

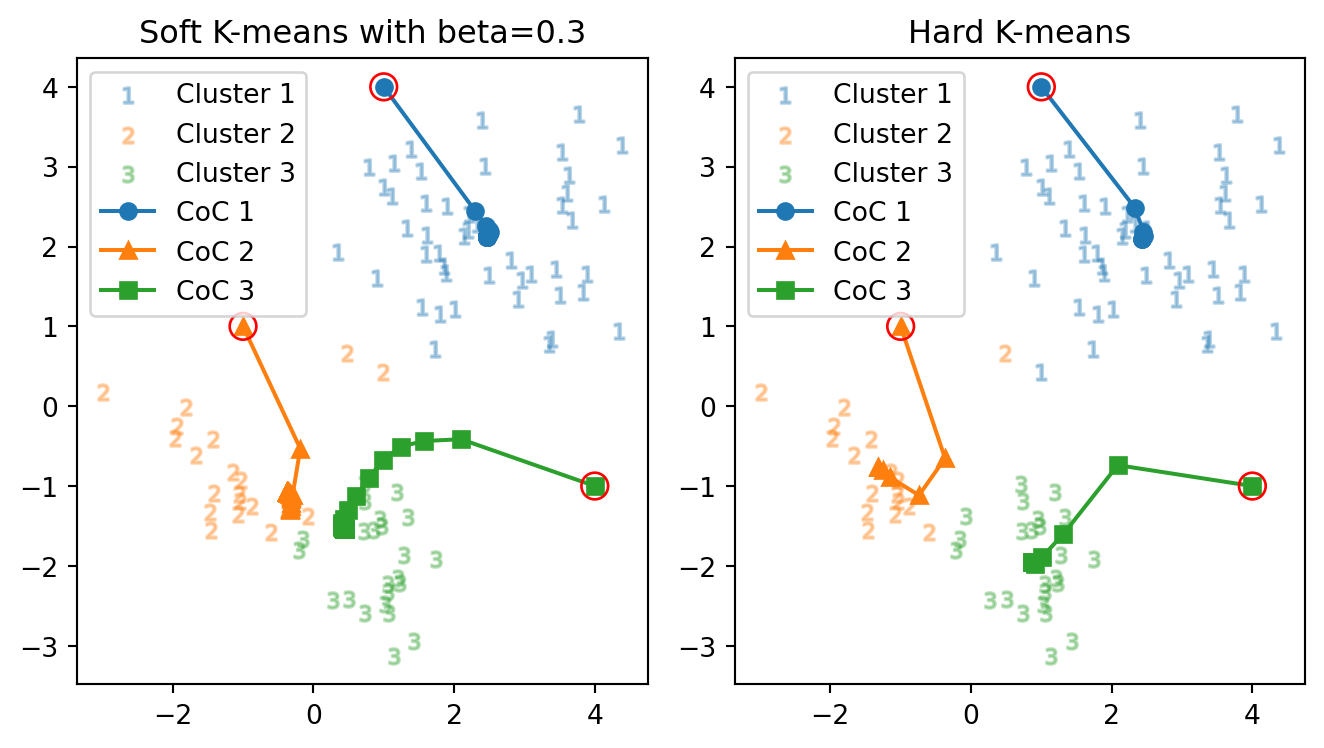
正解数: 85 vs. 85     正解率: 94.4 % vs. 94.4 %     反復数: 59 回 vs. 7 回

クラスター境界と正答率は変わらないが，反復数がやはり７回から大きく増えている．

結果はやはり 図 3 とは大きく異なっており，ハード \(K\)-平均法で観察された初期値鋭敏性が，変わらず残っている．

加えてこの場合も 図 3 のクラスター１と２と同様に，クラスター２と３の中心がほぼ一致している．

参考：最終的なクラスター中心の座標

   Cluster1  Cluster2  Cluster3
x  2.466833 -0.369537  0.447958
y  2.124961 -1.076874 -1.543758

\(\beta=0.3\) の場合のソフト \(K\)-平均法は，この例では クラスター中心が融合する傾向にある ようである．

一般に，\(\beta\) が小さく，温度が大きいほど，エネルギーランドスケープに極小点が少なくなり，クラスターは同じ場所へ収束しやすくなると予想される．

3.3 高温になるほどクラスター数は減少する

初期値を直前で用いた \[ m_1\gets\begin{pmatrix}4\\-1\end{pmatrix},\quad m_2\gets\begin{pmatrix}1\\4\end{pmatrix},\quad m_3\gets\begin{pmatrix}-1\\1\end{pmatrix}, \] で固定とし，さらに温度を上げて，逆温度を \(\beta=0.1\) としてみる．

図 5: ソフト K-平均法（左\(\beta=0.1\)，右\(\beta=1\)）によるクラスタリングの結果．初期値は \((m_1',m_2,m_3)=\left(\begin{pmatrix}4\\-1\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．

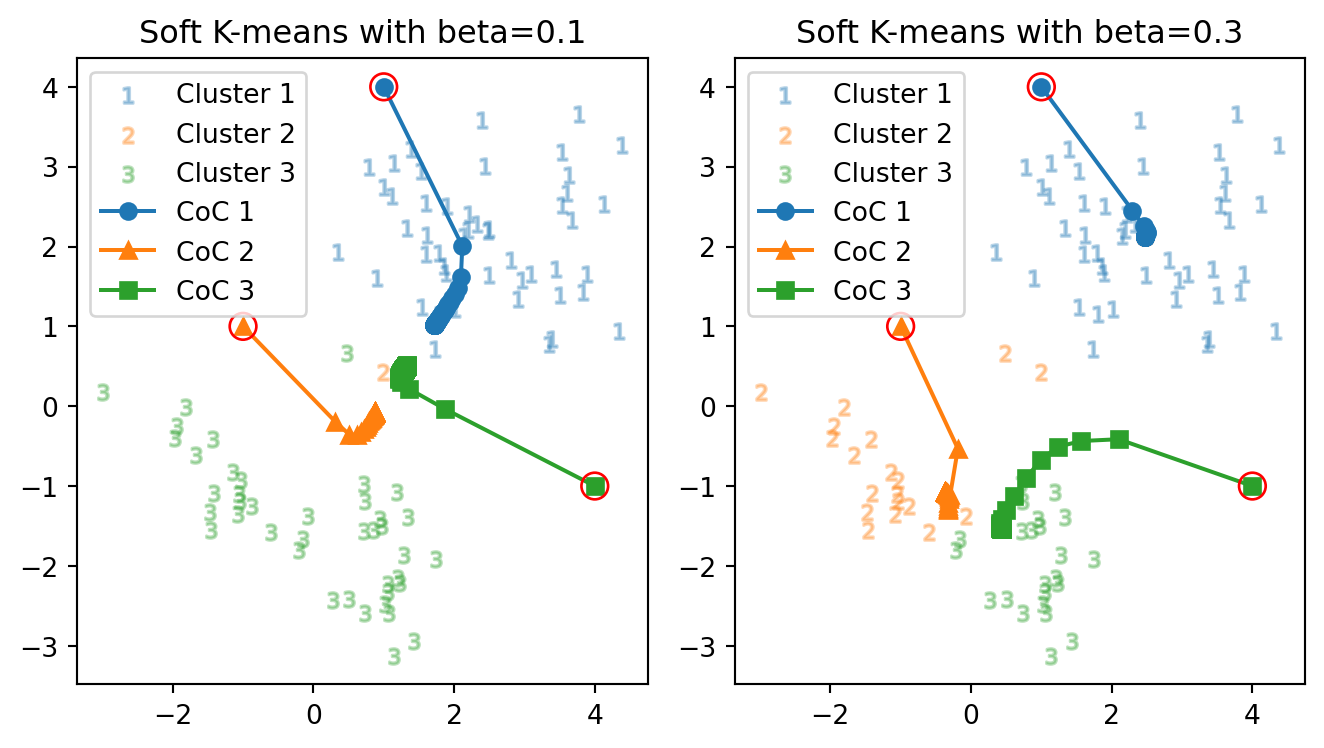
正解数: 68 vs. 85     正解率: 75.6 % vs. 94.4 %     反復数: 101 回 vs. 59 回

反復数はさらに増加し，全てがほとんど同じクラスターに属する結果となってしまった．

参考：最終的なクラスター中心の座標

   Cluster1  Cluster2  Cluster3
x  1.715903  0.862511  1.329066
y  1.012398 -0.099845  0.511186

温度が大変に高い状態では，全てが乱雑で，３つのクラスターが一様・公平に負担率を持つようになった．そのため，第一歩からほとんど全体の中心へと移動し，反復数が減る．

次に，温度を少し下げて，逆温度を \(\beta=2\) としてみる．

図 6: ソフト K-平均法（左\(\beta=10\)，右\(\beta=1\)）によるクラスタリングの結果．初期値は \((m_1',m_2,m_3)=\left(\begin{pmatrix}4\\-1\end{pmatrix},\begin{pmatrix}1\\4\end{pmatrix},\begin{pmatrix}-1\\1\end{pmatrix}\right)\)．

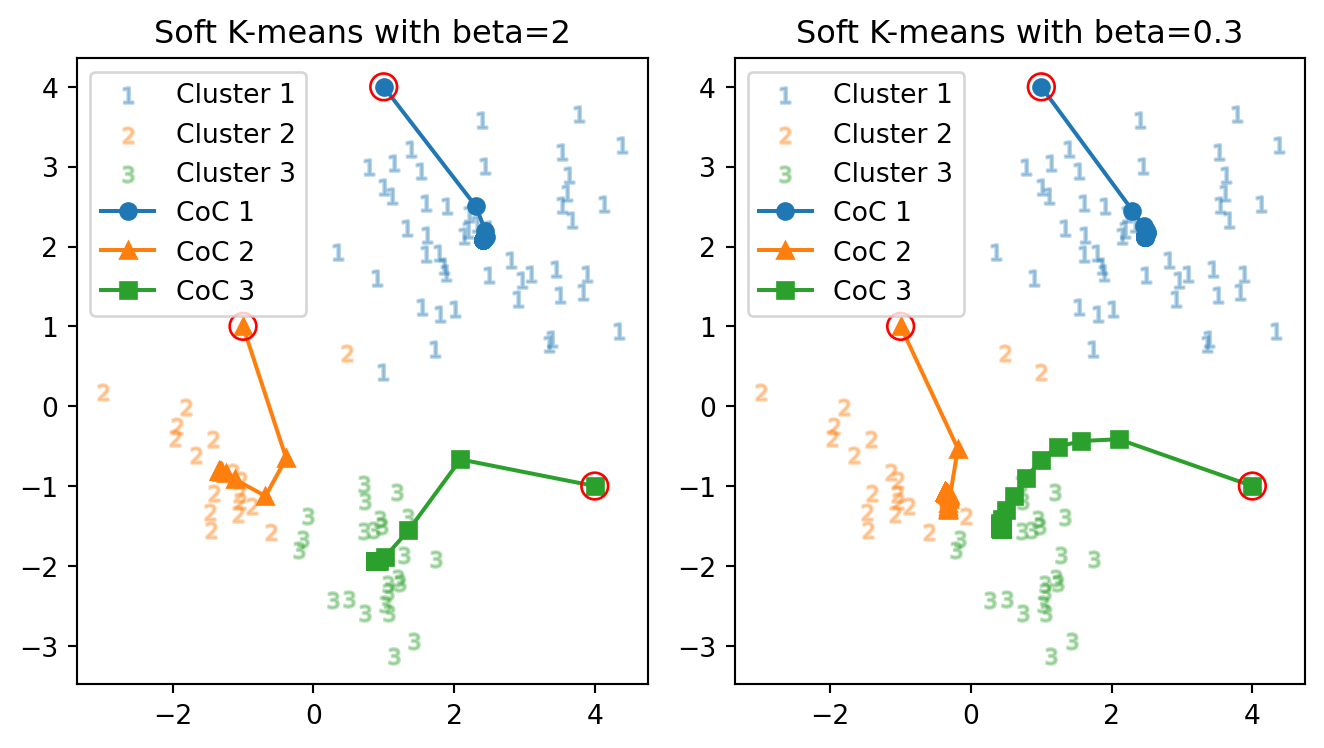
正解数: 85 vs. 85     正解率: 94.4 % vs. 94.4 %     反復数: 17 回 vs. 59 回

初めて soft \(K\)-means アルゴリズムを用いた場合で，３つのクラスター中心がはっきりと別れた．反復回数は，\(\beta=0.3\) の場合と比べればやはり落ち着いている．

しかし，正解率は head \(K\)-means の場合（ 図 2 など）と全く同じである．実は，最終的なクラスター中心も 図 2 の最終的なクラスター中心とほとんど同じになっている．

参考：最終的なクラスター中心の座標

今回のソフト \(K\)-平均法の最終的なクラスター中心

   Cluster1  Cluster2  Cluster3
x  2.416113  0.881629 -1.338782
y  2.086327 -1.934090 -0.816316

図 2 のハード \(K\)-平均法の最終的なクラスター中心

   Cluster1  Cluster2  Cluster3
x  2.426102  0.868333 -1.323353
y  2.091429 -1.948458 -0.765176

以上より，ソフト \(K\)-平均法は温度を上げるほどクラスター数が少なくなり，温度を下げるほどクラスター数は上がり，十分に温度を下げるとハード \(K\)-平均法に挙動が似通う．

3.4 最適な硬度の選択

\(\beta=0.2\) ではクラスターが２つに縮退し，\(\beta=1\) では hard \(K\)-means アルゴリズムの結果とほとんど変わらなくなる．その中間では次のように挙動が変わる：

図 7: ソフト K-平均法によるクラスタリングの結果の比較（\(\beta=0.2\) vs. \(\beta=0.25\)）．

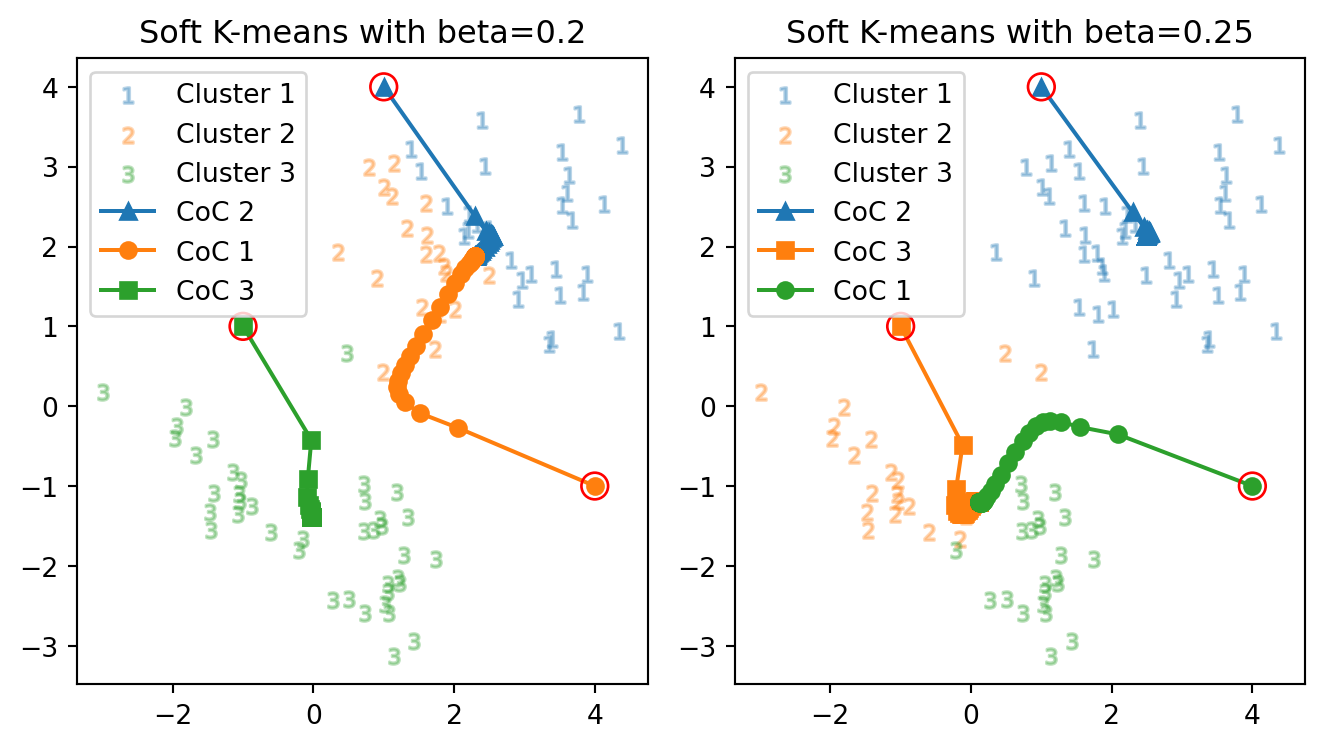
正解数: 50 vs. 86
正解率: 55.6 % vs. 95.6 %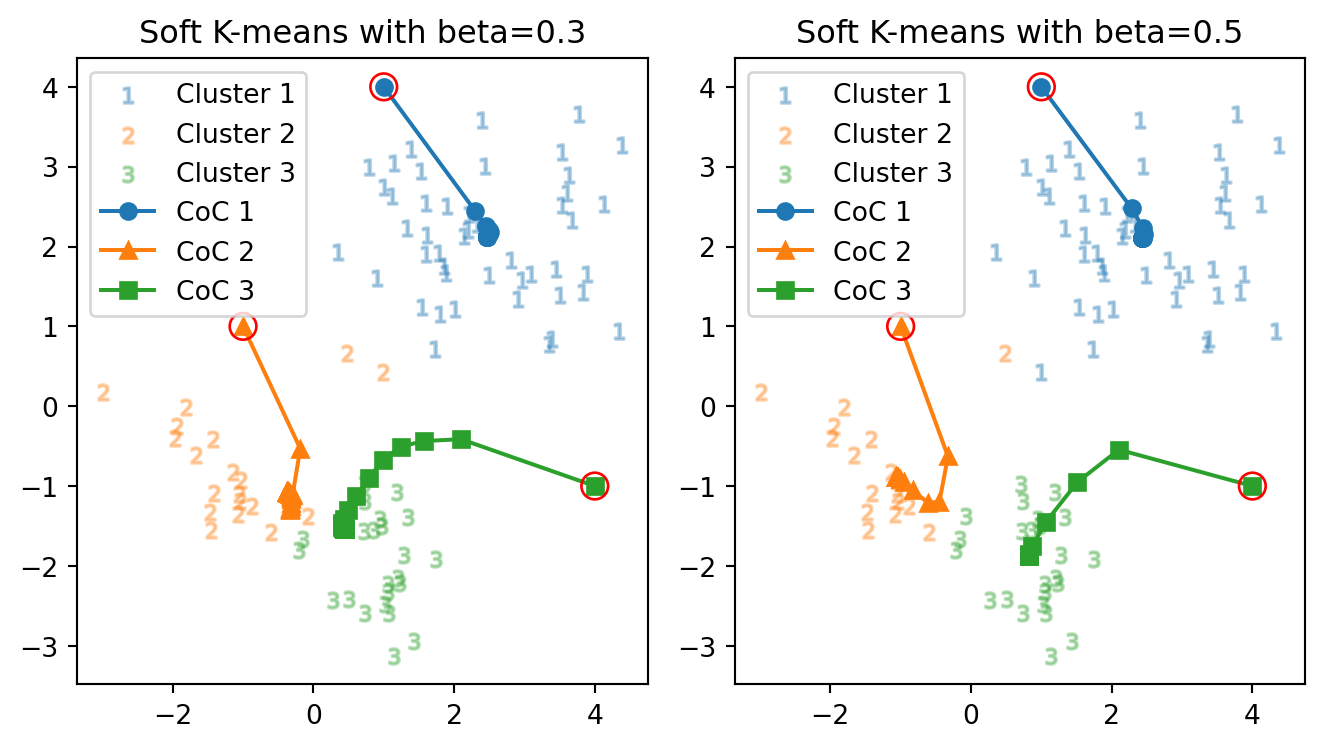

図 8: ソフト K-平均法によるクラスタリングの結果の比較（\(\beta=0.3\) vs. \(\beta=0.5\)）．

正解数: 85 vs. 85
正解率: 94.4 % vs. 94.4 %

やはり，温度が高い場合はクラスター中心が合流・融合してしまいやすいが，冷却することでクラスター数は大きい状態で安定する，と言えるだろう．

4 本番データセットでの実験

今まで使っていたデータ1.3はクラスターのオーバーラップはなかったため，いわば優しいデータであった．ここからはよりデータ生成過程が複雑なデータを用いて，ソフト \(K\)-平均法の挙動を観察する．

4.1 データの概観

今度は，次の４クラスのデータを用いる．

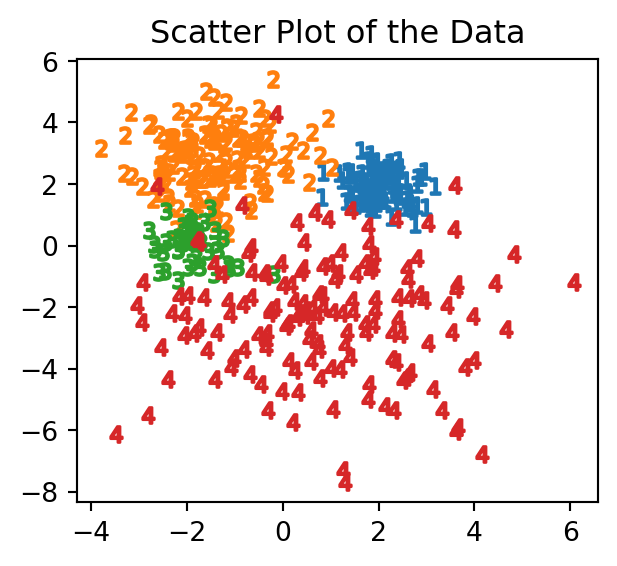
実は，これは４つの Gauss 分布から生成されたデータである．

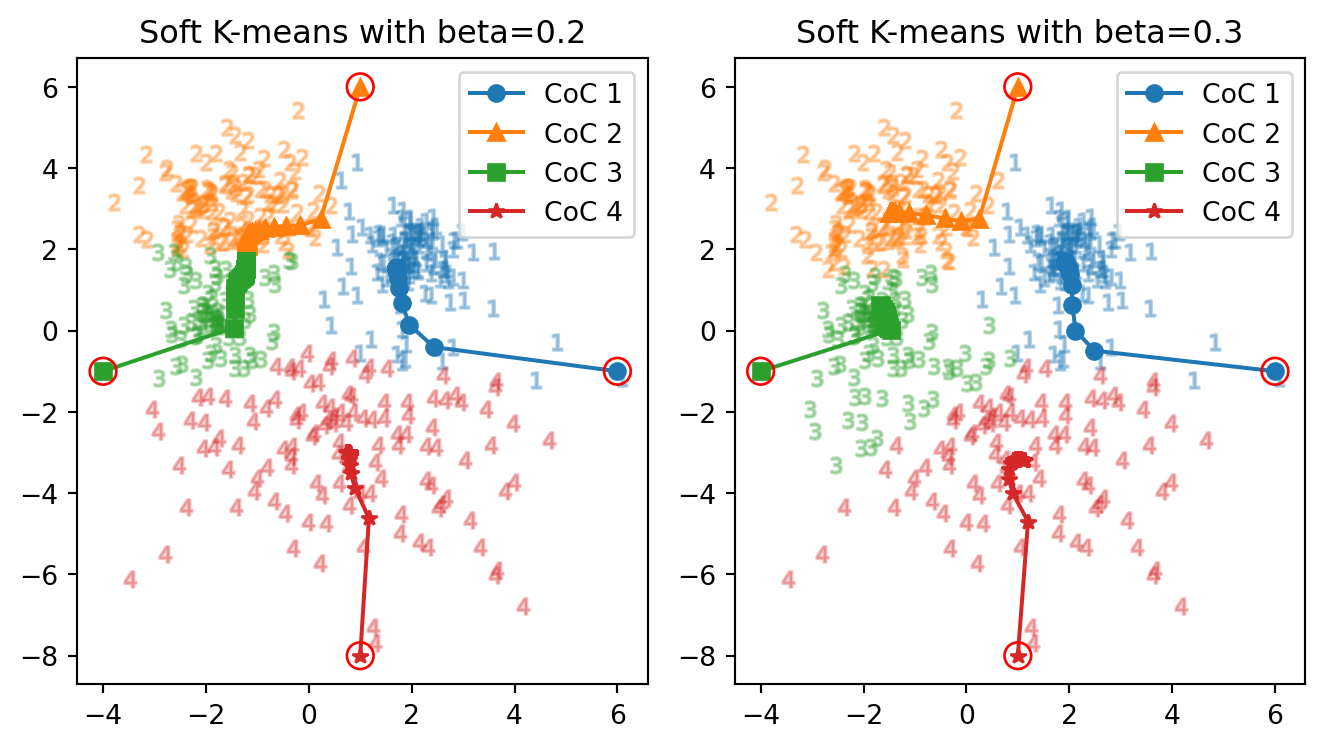
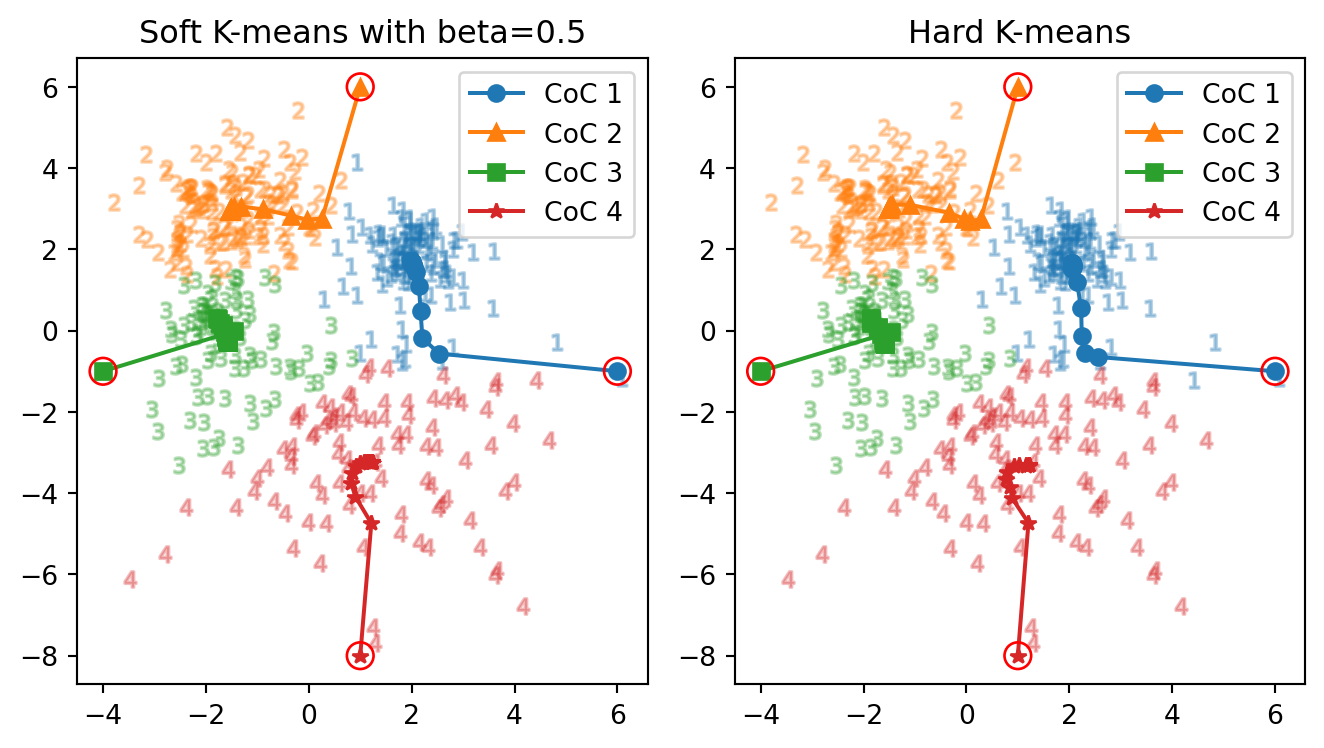
4.2 最適な温度の選択

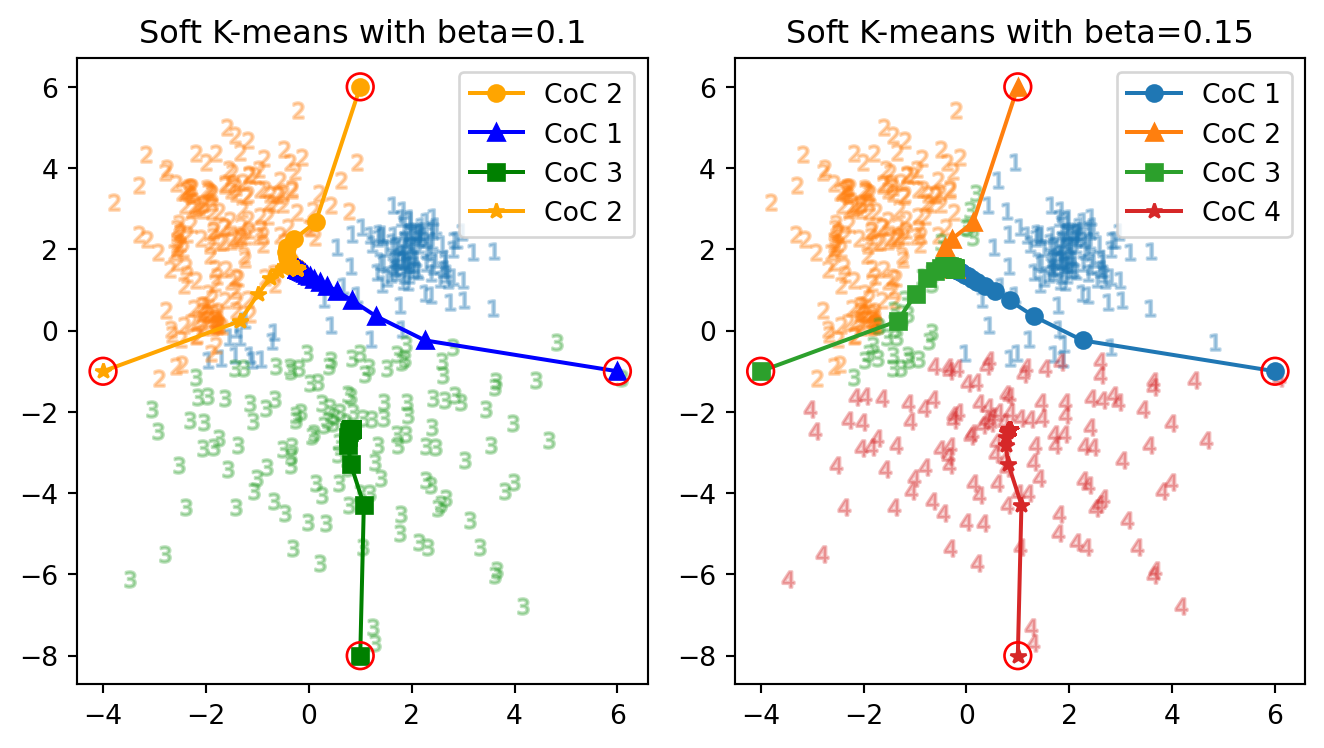
正解数: 377 vs. 366     正解率: 83.8 % vs. 81.3 %     反復数: 49 回 vs. 62 回
正解数: 386 vs. 375     正解率: 85.8 % vs. 83.3 %     反復数: 101 回 vs. 70 回
正解数: 378 vs. 378     正解率: 84.0 % vs. 84.0 %     反復数: 39 回 vs. 14 回

5 実験結果まとめ

結論

• データ 1.3 に対して，（初期値 \((m'_1,m_2,m_3)\) で）ソフト \(K\)-平均法を適用すると，
  • \(\beta\ge2\) の場合で結果はハード \(K\)-平均法と変わらなくなる．
  • \(\beta=1\) の場合で結果はクラスターがほとんど２つになり，\(\beta\le0.5\) では計算機上では実際に２つになってしまう．
  • 正答率は \(1\le\beta\le1.1\) で最大であった．
  • \(\beta\) を大きくするほど，反復回数は減少していった．
• データ 4.1 に対しても，以上の４点について同様の傾向が確認できた．

こうしてソフト \(K\)-平均法とハード \(K\)-平均法の性質は分かった．主に

1. 初期値依存性
2. クラスタ数 \(K\) の選択法

の問題が未解決であり，恣意性が残る．

これを，ベイズ混合モデリングにより解決する方法を次稿で紹介する：

References

Arthur, D., and Vassilvitskii, S. (2007). K-means++: The advantages of careful seeding. In Proceedings of the eighteenth annual ACM-SIAM symposium on discrete algorithms, pages 1027–1035. USA: Society for Industrial; Applied Mathematics.

Bishop, C. M. (2006). Pattern recognition and machine learning. Springer New York.

Gonzalez, T. F. (1985). Clustering to minimize the maximum intercluster distance. Theoretical Computer Science, 38, 293–306.

Lloyd, S. (1982). Least squares quantization in PCM. IEEE Transactions on Information Theory, 28(2), 129–137.

MacKay, D. J. C. (2003). Information theory, inference and learning algorithms. Cambridge University Press.

MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. In Proceedings of the fifth berkeley symposium on mathematical statistics and probability,Vol. 1, pages 281–297.

Murphy, K. P. (2022). Probabilistic machine learning: An introduction. MIT Press.

Footnotes

1. (MacKay, 2003, p. 285)．

2. Lloyd は 1957 年には発表していたが，論文の形になったのが 1982 である．\(K\)-means という名前の初出は (MacQueen, 1967) とされている．

3. (MacKay, 2003, p. 284)，(Bishop, 2006, p. 429)，(Murphy, 2022, p. 722) 21.3.3節．クラスター中心は 符号表ベクトル または 代表ベクトル (code-book vector) という．

4. stiffness の用語は (MacKay, 2003, p. 289) から．実は各クラスターに Gauss モデルを置いた場合の分散 \(\sigma^2\) に対して，\(\beta=\frac{1}{2\sigma^2}\) の関係がある．次稿 参照．

5. (MacKay, 2003, p. 291)．