Poisson 過程を見てみよう

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1 Poisson 過程

1.1 はじめに

Poisson 過程と言った場合，Poisson 点過程 \(\eta\) と Poisson 計数過程 \(N\) の２つを峻別する必要がある．¹

\(E=[0,T]\)，\(\lambda>0\) をレートとした場合，

• \(E\) 上の（一様な） Poisson 点過程 \(\eta\) とは，\(X_k\overset{\text{i.i.d.}}{\sim}\mathrm{U}([0,T])\) を一様確率変数，\(\kappa\sim\mathrm{Pois}(\lambda T)\) を Poisson 確率変数として， \[ \eta=\sum_{k=1}^\kappa\delta_{X_k} \] で表せる 確率核 \(\Omega\to E\) をいう．
• \(E\) 上の（一様な） Poisson 計数過程 \(N\) とは，点過程 \(\eta\) の \([0,t]\) 内の点の数 \[ N_t:=\#\left\{n\in\mathbb{N}\mid X_n\le t\right\}=\sum_{n=1}^\infty1_{\left\{X_n\le t\right\}} \] で定まる 確率過程 \(\{N_t\}\subset\mathcal{L}(\Omega)\) をいう．

このとき， \[ \eta([0,t])\sim\mathrm{Pois}(\lambda t), \] \[ N_t\sim\mathrm{Pois}(\lambda t), \] が成り立ち，\(N\) は Lévy 過程になる．

\(N\) は Lévy 過程の中でも，大きさ１の跳躍のみで増加するものとして特徴付けられる．²

\(N\) は，ランダム測度 \(\eta\) が定める \[ N_t(\omega)=\eta(\omega,[0,t])=\int_0^t\eta(\omega,ds) \] とも理解できる．

1.2 点過程の定義

定義 (point process)³

\((E,\mathcal{E})\) を測度空間とする．\(E\) 上の 点過程 とは，次の条件を満たす確率核 \(\eta:\Omega\to E\) をいう： \[ \eta(\omega,B)\in\mathbb{N}\cup\{\infty\},\qquad\omega\in\Omega,B\in\mathcal{E}. \]

従って，任意の点過程 \(\eta\) に対して，積分 \[ (\eta|f)(\omega):=\int_E\eta(\omega,dx)f(x)\in[-\infty,\infty] \] が定まる．

点過程 \(\eta\) が 真の点過程 であるとは，ある \(E\)-値確率変数の列 \(X_1,X_2,\cdots\) と，\(\mathbb{N}\cup\{\infty\}\)-値確率変数 \(\kappa\) が存在して， \[ \eta=\sum_{n=1}^\kappa \delta_{X_n}\;\;\text{a.s.} \] と表せることとする．

真の点過程になるための条件

(Revuz and Yor, 1999, p. 471) 定義XII.1.1 は違う定義を与えている：

\(E\) 上の点過程とは，\(E_\delta:=E\cup\{\delta\}\) 上の確率過程 \(\{e_t\}_{t\in\mathbb{R}_+}\subset\mathcal{L}(\Omega;E_\delta)\) であって，次の２条件を満たすものをいう：

1. \((t,\omega)\mapsto e_t(\omega)\) は \(\mathcal{B}(\mathbb{R}^+)\otimes\mathcal{F}\)-可測である．
2. \(D_\omega:=\left\{t\in\mathbb{R}_+\mid e_t(\omega)\ne\delta\right\}\) は殆ど確実に可算である．

(Kingman, 2006) の定義は「\(E\) 内のランダムに決まる可算集合」というもので，これと等価な定義である．この定義は，上で与えた確率核による定義よりも強い（範囲が狭い）ものである．

確率核の意味での点過程が，追加で次の条件を満たすとき，真の点過程になる．⁴ 特に，(Revuz and Yor, 1999) と (Kingman, 2006) の意味でも点過程である．

ある可算な分割 \(\sqcup_{n\in\mathbb{N}}B_n=E\) が存在して， \[ \operatorname{P}[\eta(B_n)<\infty]=1 \] である．

• \(E\) が Polish 空間で，\(\eta(\omega,-)\) が（殆ど確実に）任意の有界集合上で有限ならば，これを満たす．
• \(\sigma\)-有限な強度測度を持つ Poisson 過程もこれを満たす（第 1.4 節）．

例 (Cox, 1955 過程)⁵

\(\xi\) を確率核 \(\Omega\to E\) とする．すなわち，可測写像 \(\Omega\to\mathcal{P}(E)\) であるとする．このような確率核 \(\xi\) をランダム測度ともいう．

ランダム測度 \(\xi\) によって定まる強度測度を持った Poisson 過程 \(\eta\) を，Cox 過程 または二重確率 Poisson 過程という．

式で表すと，強度測度 \(\lambda\) を持つ Poisson 点過程の分布を \(\Pi_\lambda\in\mathcal{P}(E)\) とすると， \[ \eta|\xi\overset{\text{d}}{=}\Pi_\xi \] を満たす点過程 \(\eta:\Omega\to E\) をいう．

例えば，Poisson 過程のレート関数を Gauss 過程によってモデリングした場合，これは Cox 過程によりモデリングしていることになる．⁶

1.3 強度測度

点過程には「各集合 \(B\in\mathcal{E}\) に平均何個の点が入るか」を表す 強度測度 \(\lambda\) が定まる．平均測度 とも呼ばれる．

この強度測度 \(\lambda\) は \(\operatorname{E}[d\eta]\) のようなものであり，Fubini の定理のような性質 \[ \operatorname{E}\left[\int_E u\,d\eta\right]=\int_Eu\operatorname{E}[d\eta] \] が成り立つ．これを Campbell の公式 という．

定義 (intensity / mean measure)⁷

\(\eta\) を可測空間 \((E,\mathcal{E})\) 上の点過程とする．\(\eta\) の 強度測度 とは，次で定まる測度 \(\lambda:\mathcal{E}\to[0,\infty]\) をいう： \[ \lambda(B):=\operatorname{E}[\eta(B)],\qquad B\in\mathcal{E}. \]

命題 (Campbell, 1909 の公式)⁸

\(\eta\)　を点過程，\(\lambda\) をその強度測度とする．任意の \(u\in\mathcal{L}(E)\) について，\((\eta|u)\) は確率変数であり，加えて \(u\in\mathcal{L}^1(\lambda)\) または \(u\ge0\) である場合，次が成り立つ： \[ \operatorname{E}\left[\int_Eu(x)\eta(dx)\right]=\int_Eu(x)\lambda(dx). \]

証明

\(u\) がある \(B\in\mathcal{E}\) の特性関数 \(u=1_B\) である場合， \[ \int_Eu(x)\eta(dx)=\eta(B) \] であり，点過程 \(\eta\) の定義からこれは確率変数である．

期待値の線型性より一般の単関数，単調収束定理より一般の可測関数についても成り立つ．

\(u\in\mathcal{L}^1(\lambda)\) であるとき，\(u\) に収束する単関数列 \[ u_n:=\sum_{i=1}^{m_n}a_i^{(n)}1_{B_i^{(n)}}\nearrow u \] を取ると，Lebesgue の優収束定理より次のように結論づけられる： \[\begin{align*} \operatorname{E}\left[\int_Eu(x)\eta(dx)\right]&=\lim_{n\to\infty}\operatorname{E}\left[\int_Eu_n(x)\eta(dx)\right]\\ &=\lim_{n\to\infty}\operatorname{E}\left[\sum_{i=1}^{m_n}a_i^{(n)}\eta(B_i^{(n)})\right]\\ &=\lim_{n\to\infty}\sum_{i=1}^{m_n}a_i^{(n)}\lambda(B_i^{(n)})\\ &=\int_Eu(x)\lambda(dx)=(\lambda|u)<\infty. \end{align*}\]

\(u\ge0\) の場合も同様で，Lebesgue の優収束定理が単調収束定理に変わるのみである．

1.4 Poisson 点過程の定義

定義 (Poisson (point) process / random measure)⁹

\((E,\mathcal{E})\) を可測空間，\(\lambda:\mathcal{E}\to[0,\infty]\) を測度とする．強度（測度） \(\lambda\) を持つ Poisson 過程 とは，次の２条件を満たす点過程 \(\eta\) をいう：

1. 任意の \(B\in\mathcal{E}\) に対して，\(\eta(B)\sim\mathrm{Pois}(\lambda(B))\)．
2. 任意の \(m\in\mathbb{N}\) と互いに素な可測集合 \(B_1,\cdots,B_m\in\mathcal{E}\) について，\(\eta(B_1),\cdots,\eta(B_m)\) は独立である．

２つの強度測度 \(\lambda,\lambda'\) は \(\sigma\)-有限であるとする．

このとき，\(\lambda=\lambda'\) ならば，これを強度とする Poisson 過程は分布同等である．¹⁰

加えて，\(\sigma\)-有限な強度測度を持つ Poisson 過程は，真の点過程（と同分布）である：

命題（Poisson 過程が真の点過程となるとき）¹¹

\(\lambda\) を \(\sigma\)-有限とする．このとき，ある確率変数の列 \(\{X_n\}\subset\mathcal{L}(\Omega;E)\) と \(\mathbb{N}\cup\{\infty\}\)-値確率変数 \(\kappa\) が存在して， \[ \eta:=\sum_{n=1}^\kappa\delta_{X_n} \] は強度 \(\lambda\) の Poisson 過程となる．

実は Poisson 点過程は，Poisson 分布と同様に，可算な範囲で再生性がある：\(\eta^{(1)},\eta^{(2)},\cdots\) を独立な Poisson 点過程とすると， \[ \eta:=\sum_{k=1}^\infty\eta^{(k)} \] も Poisson 点過程であり，強度測度は \(\nu:=\sum_{k=1}^\infty\lambda^{(k)}\) となる．¹²

従って，実際は \(\sigma\)-有限な強度測度を持つ Poisson 過程よりもさらに一般的な設定で上の定理が成り立つ．

1.5 例

• 強度測度が有限であるとき，複合二項過程として極めて明瞭な理解ができる．

• 区間上の Poisson 過程は，一様分布に関する複合二項過程になる．点の間の間隔は指数分布に従う．¹³

1.5.1 複合二項過程

\(\mu\in\mathcal{P}(E),\pi\in\mathcal{P}(\mathbb{N})\) とする．\(X_k\overset{\text{i.i.d.}}{\sim}\mu\) と \(\kappa\sim\pi\) について， \[ \eta:=\sum_{k=1}^\kappa\delta_{X_k} \] は点過程を定める．これを サンプリング分布 \(\mu\) を持った \(\pi\) による 複合二項過程 という．¹⁴

ある \(\gamma>0\) に関して \(\pi=\mathrm{Pois}(\gamma)\) と取った場合，\(\eta\) は強度 \(\gamma\mu\) を持った Poisson 過程となる．

複合二項過程について，次が成り立つ：

命題（有限な強度を持つ Poisson 過程の特徴付け）¹⁵

\(\lambda:\mathcal{E}\to(0,\infty)\) を有限測度とする．このとき，点過程 \(\eta\) について，次の２条件は同値である：

1. \(\eta\) は \(\lambda\) を強度測度とする Poisson 過程である．
2. サンプリング分布 \(\mu:=\lambda(E)^{-1}\lambda\) を持つ \(\mathrm{Pois}(\lambda(E))\)-複合二項過程である．

特に，\(\eta(E)=m\) で条件づけた分布は，\(\delta_{X_1}+\cdots+\delta_{X_m}\) に等しい．

1.5.2 \(\mathbb{R}_+\) 上の Poisson 過程

\(\mathbb{R}_+\) の Poisson 過程で，強度が \(\mathbb{R}_+\) 上の Lebesgue 測度の定数倍であるものを 一様 Poisson 過程 といい，\(\lambda>0\) を レート ともいう．

命題（\(\mathbb{R}_+\) 上の Poisson 点過程の特徴付け）¹⁶

\(\eta\) を \(\mathbb{R}_+\) 上の点過程とする．このとき，\(\lambda>0\) に関して次は同値：

1. \(\eta\) はレート \(\lambda\) を持った一様 Poisson 過程である．
2. 到着時刻 \[ T_n(\omega):=\inf\left\{t\ge 0\mid \eta(\omega,[0,t])\ge n\right\} \] の間隔は \(\operatorname{Exp}(\lambda)\) の独立同分布である．

1.6 印付き過程

定義 (\(K\)-marked process)¹⁷

\(\eta\) を \(E\) 上の真の点過程，\(K:E\to F\) を確率核，\(\{Y_n\}\subset\mathcal{L}(\Omega;F)\) を確率変数列とする．加えて，任意の \(m\in\mathbb{N}\cup\{\infty\}\) について，\(\kappa=m\) と \(X_1,\cdots,X_m\) の値で条件づけた \(Y_i\) の分布は，もはや \(X_i\) の値にしか依らずに独立に定まるとする： \[ (Y_n)_{n\le m}\,|\,\kappa=m,(X_n)_{n\le m}\overset{\text{d}}{=}\otimes_{n=1}^mK(X_n,-) \] このとき，\(E\times F\) 上の真の点過程 \[ \xi:=\sum_{n=1}^\kappa\delta_{(X_n,Y_n)} \] を \(X\) の \(K\) で印付けられた過程 または \(K\)-付印過程という．

\(\eta\) を \(\sigma\)-有限な強度 \(\lambda\) を持つ Poisson 過程とするとき，\(\eta\) の任意の可測写像 \(T:E\to F\) による像は \(T_*\lambda\) を強度とする Poisson 過程となり，\(\eta\) の任意の \(K\)-印付き過程もやはり Poisson 過程になる．¹⁸

\(K:E\to\mathcal{P}(F)\) が定値関数になる場合（すなわち \(\{Y_n\}\) が \(X_n\) の値に依らずに独立同分布に定まる場合），これを 独立 \(K\)-付印 という．

例（降水量の時系列）

雨がふるという事象が Poisson 点過程に従い，その際の降水量がランダムに決まるため，降水量の時系列は古くから独立付印 Poisson 過程としてモデル化されている (Todorovic and Yevjevich, 1969)．¹⁹

例（待ち行列過程）

顧客が特定のタイミング \(T_n\) でのみ到着するとした場合，その際の人数 \(N_n\) との組 \((T_n,N_n)\) は付印 Poisson 過程としてモデル化できる (Brémaud, 1981, pp. 233 例3)．

例（ニューロン発火の時系列）

(R. Shibue and Komaki, 2017), (F. Shibue Ryohei AND Komaki, 2020) にて，ニューロン集団の発火特性の推定に応用されている．

命題（一様 Poisson 過程の独立付印過程の特徴付け）

\[ \xi=\sum_{n=1}^\infty1_{\left\{T_n<\infty\right\}}\delta_{(T_n,Y_n)} \] を \(\mathbb{R}_+\times E\) 上の点過程， \[ \eta=\sum_{n=1}^\infty1_{\left\{T_n<\infty\right\}}\delta_{T_n} \] を \(\mathbb{R}_+\) 上の点過程とする．

\(\gamma>0\) と \(\mu\in\mathcal{P}(E)\) について，次は同値：

1. \(\xi\) はレート \(\gamma\) を持つ一様 Poisson 過程 \(\eta\) の \(\mu\)-独立付印である．
2. \(T_1,Y_1,T_2-T_1,Y_2,\cdots\) は独立で，\(T_n-T_{n-1}\sim\operatorname{Exp}(\gamma)\) かつ \(Y_n\overset{\text{i.i.d.}}{\sim}\mu\) である．

1.7 剪定

定義 (\(p\)-thinning)²⁰

\(p:E\to[0,1]\) を可測関数とし，確率核 \(K:E\to2\) を次で定める： \[ K_p(x,-):=\biggr(1-p(x)\biggl)\delta_0+p(x)\delta_1. \]

\(E\) 上の真の点過程 \(X\) の，この確率核に関する \(E\times2\) 上の \(K\)-印付き過程 \(M\) に対して， \[ (\omega,B)\mapsto M(\omega,B\times\{1\}) \] で定まる \(E\) 上の真の点過程を \(X\) の \(p\)-剪定 という．

すなわち，点 \(x\in E\) に定まる所定の確率 \(p(x)\) に関して，確率 \(p(X_n)\) で点 \(X_n\) を脱落させて得る点過程を，\(p\)-剪定という．

\(p\)-剪定は強度 \(p(x)\lambda(dx)\) を持つ Poisson 過程となる．加えて，\(1-p\)-剪定と違いに独立になる．²¹

例（非一様な Poisson 過程のシミュレーション）

この剪定によって，連続なレート関数 \(\lambda\) を持つ非一様な Poisson 過程をシミュレーションする方法が (Lewis and Shedler, 1979) で提案され，(Ogata, 1981) が一般の点過程に拡張した．

実際，yuimaでもこの方法が採用されている（第 1.9.2 節）．

アルゴリズムは次のとおりである：

\(\lambda\le\lambda^*\) を満たす２つのレート関数を持つ Poisson 過程 \(\eta,\eta^*\) を考える．\(\eta^*([0,x_0])\) 内の点 \[ X_1^*,X_2^*,\cdots,X_{\eta^*([0,x_0])}^* \] を生成し，それぞれの点を確率 \(1-\frac{\lambda(X_i^*)}{\lambda^*(X_i^*)}\) で取り除く．すると，残った点は \[ \frac{\lambda(X_i^*)}{\lambda^*(X_i^*)}\lambda^*(dx)=\lambda(dx) \] をレート関数にもつ Poisson 過程の分布，すなわち \(\eta\) の分布に従う．

最も簡単な場合としては，\(\lambda^*:=\max_{t\in[0,x_0]}\lambda(t)\) などと取れば良いが，\(\lambda\) が変動が激しい関数である場合，より効率が良い方法があるかもしれない．

すると，定値なレート関数を持つ Poisson 過程 \(\eta^*\) は，指数分布に従う確率変数をシミュレーションすることなどによって得られる（命題 1.5.2）．

1.8 Poisson 過程に関する積分

1.8.1 直接の積分

命題（Poisson 点過程との積分が定まるための条件）²²

\((E,\mathcal{E},\lambda)\) を \(\sigma\)-有限な測度空間，\(\eta\) を \(E\) 上の強度測度 \(\lambda\) を持つ Poisson 点過程とする．

このとき，\(f\in\mathcal{L}(E)_+\) について，次は同値：

1. \(\operatorname{P}[(\eta|f)<\infty]=1\)．
2. 次が成り立つ： \[ \int_E(f\land1)d\lambda<\infty. \]

また，これらの条件が成り立たないとき，\(\operatorname{P}[(\eta|f)=\infty]=1\) が成り立つ．

従って，\(f\in\mathcal{L}^1(\lambda)\) に関して，\((\eta|f)\) は殆ど確実に有限になる．

1.8.2 補過程に関する積分

加えて，中心化された積分 \[ I(f):=(\eta|f)-(\lambda|f)\in L^2(\operatorname{P}) \] は \(L^1(\lambda)\cap L^2(\lambda)\) 上の等長作用素で，\(L^2(\lambda)\) 上に有界延長する．²³

1.8.3 Poisson 積分の分布

命題（Poisson 積分の分布）²⁴

\((E,\mathcal{E})\) を可測空間，\(\eta\) を有限な強度測度 \(\lambda\) を持つ Poisson 点過程とする．このとき，\(\eta\) に関する \(h\in\mathcal{L}^1(\lambda;\mathbb{R}^d)\) の積分 \[ (\eta|h)(\omega)=\int_Eh(z)\eta(\omega,dz) \] の第二キュムラント母関数は，次のように表される： \[\begin{align*} \psi(u)&=\int_E\biggr(e^{i(u|h(z))}-1\biggl)\lambda(dz)\\ &=\int_{\mathbb{R}^d}\biggr(e^{i(u|x)}-1\biggl)(h_*\lambda)(dx). \end{align*}\] すなわち，\((\eta|h)\) は複合 Poisson 分布 \(\mathrm{CP}(\|h_*\lambda\|_\mathrm{TV},\|h_*\lambda\|_\mathrm{TV}^{-1}h_*\lambda)\) に従う，平均 \((\lambda|h)\)，分散 \((\lambda|h^2)\) の確率変数である．

1.9 Poisson 計数過程のシミュレーション

yuimaパッケージでは，Poisson 計数過程は複合 Poisson 計数過程の特別な場合として扱うため，シミュレーション法は第 2.5 節で扱い，ここでは結果のみを示す．

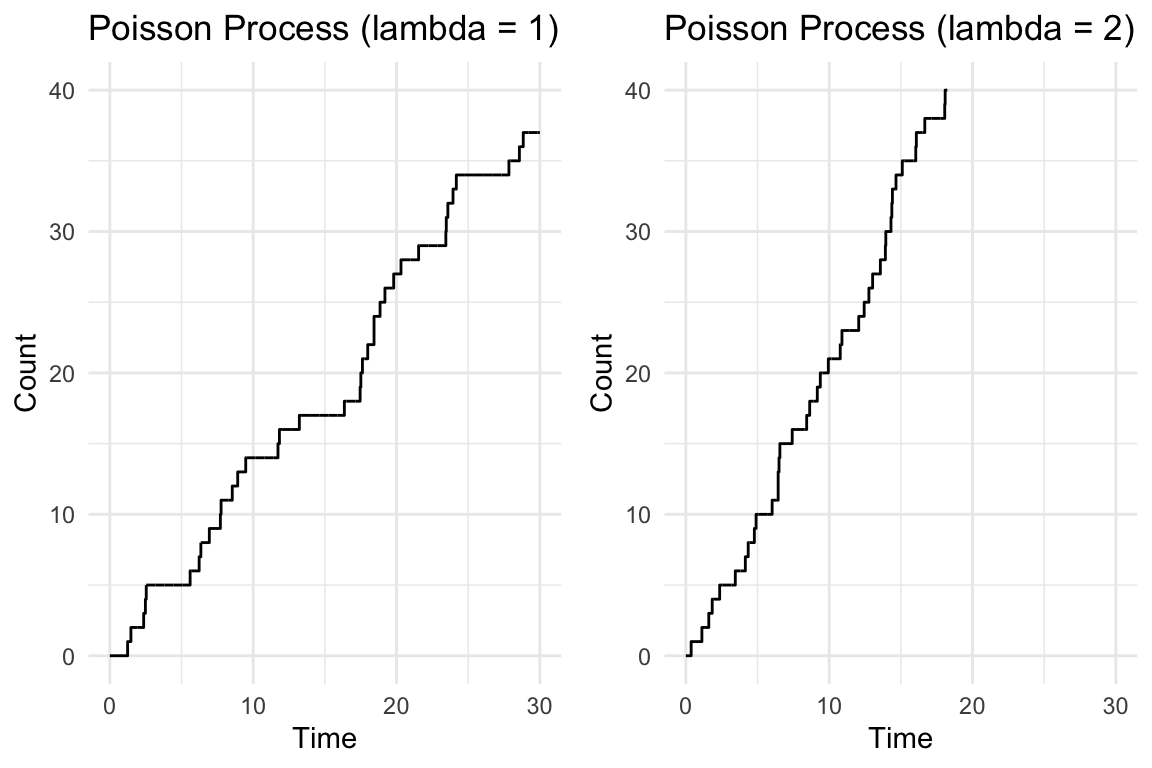
1.9.1 一様な Poisson 計数過程

強度 \(\lambda>0\) を持つ（一様な） Poisson 計数過程とは，\(\mathbb{R}_+\) 上のレート \(\lambda>0\) を持つ一様な Poisson 点過程（第 1.5.2 節）\(\eta\) に対して， \[ N_t(\omega):=\eta(\omega,[0,t]) \] で定まる Lévy 過程である．

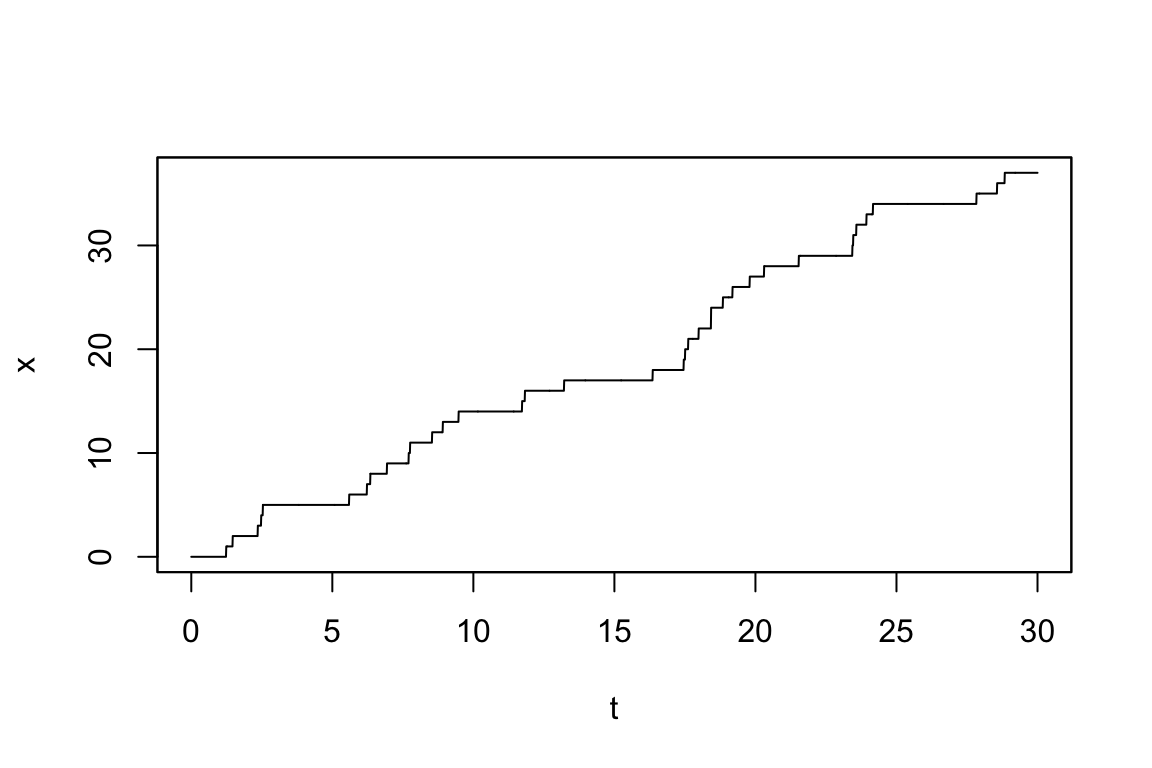
レート \(\lambda>0\) はジャンプの頻度を表している：

1.9.2 非一様な Poisson 計数過程

強度関数 \(\lambda:\mathbb{R}_+\to\mathbb{R}^+\) を持つ 非一様な Poisson 計数過程 とは，全く同様な定義 \[ N_t(\omega):=\eta(\omega,[0,t]) \] をし，ただ \(\eta\) の強度測度を \(\lambda(t)\ell_+(dt)\) に置き換えたものである．

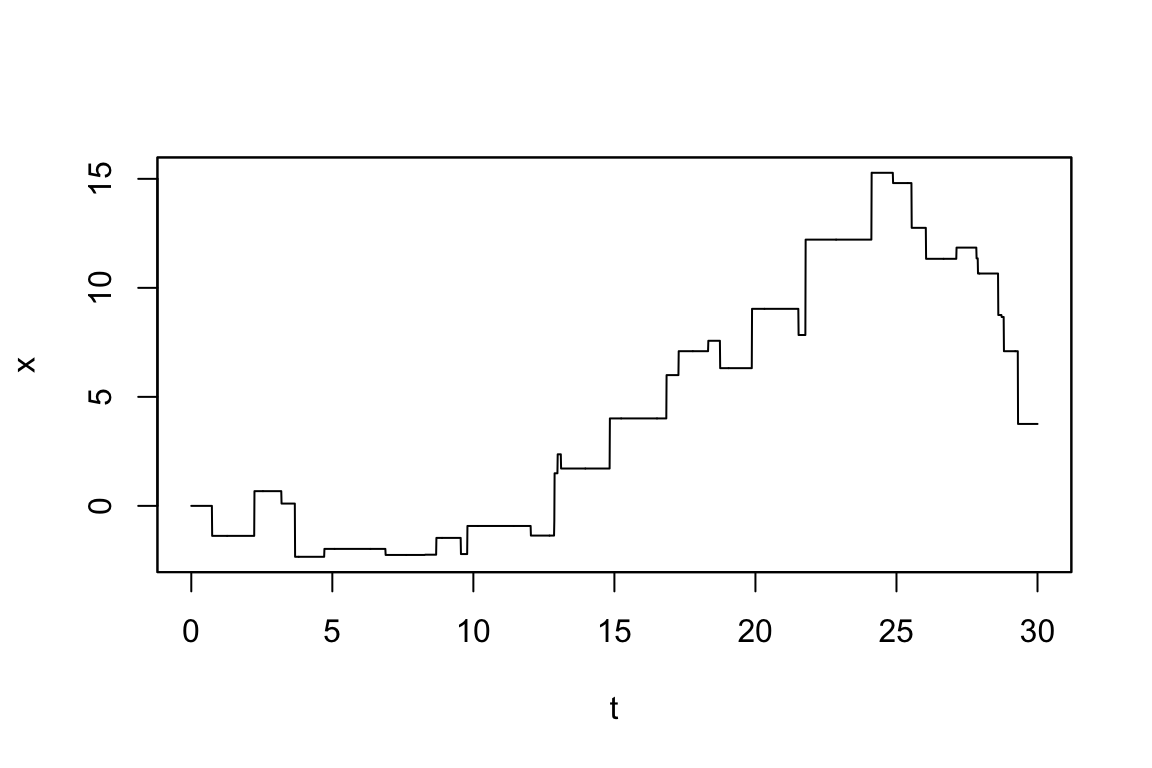
例えば，強度関数 \[ \lambda(t)=10e^{-\frac{t}{5}} \] を持つ非一様な Poisson 過程は次のような見本道を持つ：

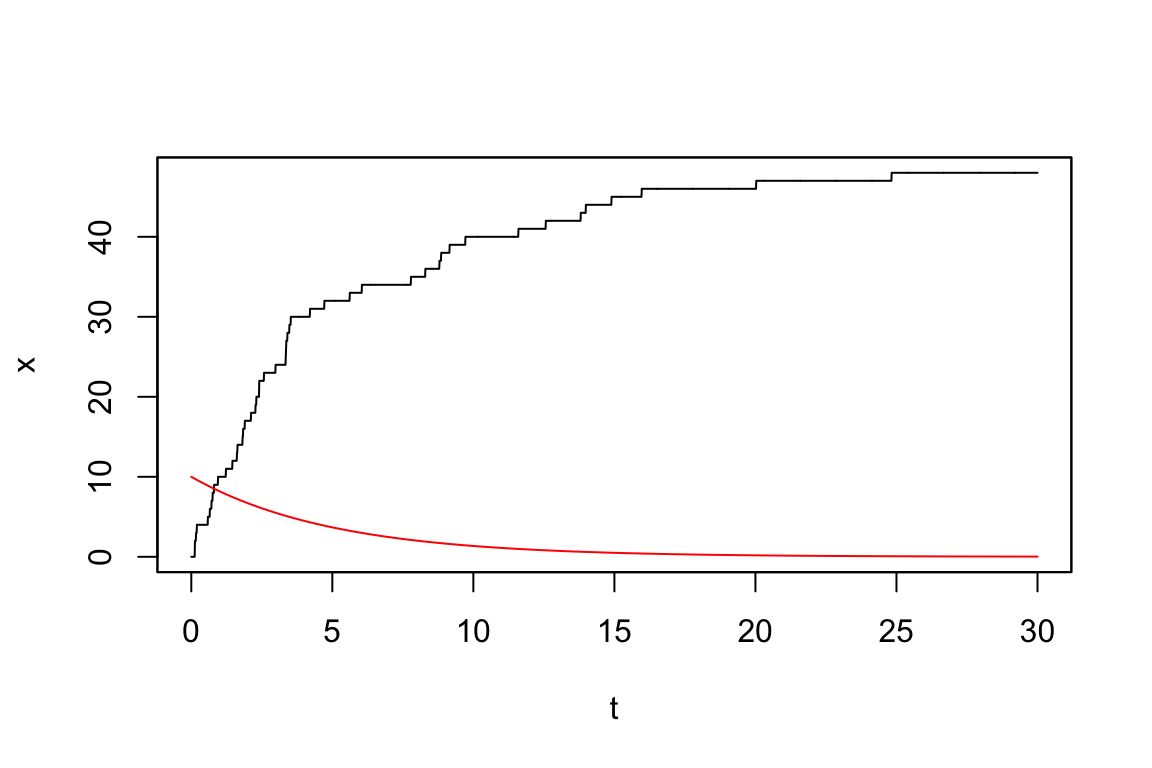
時間が経つごとに強度関数 \(\lambda\) の値（赤線）が小さくなり，それに伴ってジャンプの頻度が減少していくことがわかる．

2 複合 Poisson 過程

2.1 はじめに

点過程としての複合 Poisson 過程は，印付けられた Poisson 点過程（第 1.6 節）から構成される．

2.1.1 計数過程として

Poisson 過程 \(N\) は，大きさ１の跳躍のみで増加する Lévy 過程として特徴付けられるのであった．

この跳躍の大きさを任意の確率分布 \(\mu\in\mathcal{P}(\mathbb{R})\) に従ったものに変更したもの \[\begin{align*} M_t&:=\sum_{n=1}^{N_t}Y_n\\ &=\sum_{k=1}^\kappa Y_k1_{\left\{X_k\le t\right\}} \end{align*}\] が 複合 Poisson （計数）過程 \(\mathrm{CP}(\lambda,\mu)\) である．²⁵

\(\mu=\delta_1\) の場合が Poisson 過程に当たる．²⁶

注（従属操作による見方）²⁷

\(Y_n\overset{\text{i.i.d.}}{\sim}\mu\) について，これが定めるランダムウォーク \[ S_n:=\sum_{k=1}^nY_k \] を 再起過程 (renewal process) という．²⁸

\(\mu=\operatorname{Exp}(\lambda)\) の場合の再起過程が定める計数過程 \[ N_t:=\sum_{n=0}^\infty1_{[0,t]}(S_n) \] が Poisson 過程なのであった．

これに対して，\(N_t\) を従属過程とした従属 \(M_t:=S_{N_t}\) が複合 Poisson 過程 \(\mathrm{CP}(\lambda,\mu)\) と理解できる．

2.1.2 点過程として

この複合 Poisson 過程は，印付けられた Poisson 過程 \[ \eta:=\sum_{n=1}^\kappa\delta_{(X_n,Y_n)} \] が \(E\times\mathbb{R}\) 上の強度測度 \(\mu\otimes\lambda\ell\) を持つ Poisson 点過程であり，各 \(X_n\) に \(Y_n\) の重みをつけて足し合わせた点過程 \[ \xi(\omega,B):=\int_{B\times\mathbb{R}}r\,\eta(\omega,dydr) \] が基になっている．

これが複合 Poisson 点過程であり，\(\xi\) に関する積分として \(M\) が理解できる（第 1.8.1 節参照）： \[ M_t(\omega)=\xi(\omega,[0,t])=\int^t_0\xi(\omega,ds). \]

注（Lévy 過程としての複合 Poisson 過程）²⁹

一様 Poisson 過程は定数の Lévy 測度 \(\lambda>0\) を持つ，特性量 \((0,0,\lambda\delta_1)\) が定める Lévy 過程である．

一方で，一様な複合 Poisson 過程 \(\mathrm{CP}(\lambda,\mu)\) は特性量 \((0,0,\lambda\mu)\) を持つ Lévy 過程である．

従って，Lévy 測度 \(\nu\) について，\(\|\nu\|_\mathrm{TV}\) はジャンプの頻度，\(\|\nu\|_\mathrm{TV}^{-1}\nu\) がジャンプの分布を表すと言える．

しかし，一般に Lévy 測度は，\(\left\{z\in\mathbb{R}^d\mid\lvert z\rvert>\epsilon\right\}\) 上では有限であっても，\(\mathbb{R}^d\setminus\{0\}\) 上で有限とは限らない．\(\mathbb{R}^d\setminus\{0\}\) 上でも有限である場合，跳躍部分は定義 2.4.1 の意味でも複合 Poisson 過程である．

すなわち，有限時区間内では（殆ど確実に）有限回しかジャンプしない純粋跳躍 Lévy 過程は，全て一様な複合 Poisson 計数過程である．³⁰

一般の Lévy 測度を持つ Lévy 過程は，一様な複合 Poisson 部分を跳躍部分にもつ Lévy 過程の，広義 \(\mathbb{H}^2\)-収束極限として表される．³¹

2.1.3 複合 Poisson 点過程の普遍性

違いに素な \(A,B\in\mathcal{E}\) に対して \(\xi(A)\perp\!\!\!\perp\xi(B)\) を満たすようなランダム測度 \(\xi\) は，固定した原子を持たないならば，ある決定論的な測度と複合 Poisson 点過程の和として表せる．³²

2.1.4 点過程と計数過程の峻別

ここでも \(\xi\) と \(M\) は全く異なる数学的対称であり，区別を要する．

特に，\(\xi\) は確率核，\(M\) は Lévy 過程である．

しかし，Lévy 過程に関する確率積分を定義する際，２つの概念は密接に関連する．

Lévy 過程が駆動する確率積分

というのも，\(\xi\) の背後には，拡張された空間 \(E\times\mathbb{R}^+\) 上の Poisson 点過程 \(\eta\) があり，\(M\) と \(\eta\) が密接に関連するのである．

\(M\) に関する確率積分は \[ dM_t=\eta(dzdt) \] と理解でき，\(\eta\) のランダム測度としての理解が活躍する．

\(\eta\) の平均測度は \(\nu\otimes\ell_+\) と表され，この \(\nu\) を Lévy 測度という．

すなわち，Lévy 過程に関する確率積分とは，Lévy 過程に付随する Poisson 点過程に関する確率積分に他ならない．

2.2 複合 Poisson 点過程の定義

2.2.1 一般的な定義

定義 (compound Poisson process)³³

\((E,\mathcal{E})\) を可測空間とする．\(E\) 上の 複合 Poisson 分布 とは，\(E\times(\mathbb{R}\setminus\{0\})\) 上の Poisson 過程 \(\eta\) を用いて \[ \xi(\omega,B)=\int_{B\times\mathbb{R}\setminus\{0\}}r\,\eta(\omega,dydr), \] \[ B\in\mathcal{E}, \] と表せる確率核 \(\xi:\Omega\to E\) をいう．

\(E\times\mathbb{R}\setminus\{0\}\) 上の Poisson 点過程 \(\eta\) の第二成分が，\(E\) 上のランダム点の「重み」のようなもので，\(\xi\) は重みをつけて点を積分したものと理解できる．これは一般化された Poisson 複合の手続きに思える．

\(\mathbb{R}^d\) 上の複合 Poisson 分布

上述の定義を，\(\mathbb{R}^d\) 上の分布 \(\mu\in\mathcal{P}(\mathbb{R}^d)\) の Poisson 複合 \(\mathrm{CP}(\lambda,\mu)\in\mathcal{P}(\mathbb{R}^d)\) と比較してみよう．

これは \[ X:=\sum_{n=1}^NZ_n,\qquad Z_n\overset{\text{i.i.d.}}{\sim}\mu,N\sim\mathrm{Pois}(\lambda) \] で定まる \(X\) の分布であり，特性関数は \[ \varphi_X(u)=\exp\left(\lambda\int_{\mathbb{R}^d}\biggr(e^{i(u|y)}-1\biggl)\mu(dy)\right) \] で与えられる．

複合 Poisson 過程はこれを過程に一般化したものであり，Poisson 複合の部分は \(E\times\mathbb{R}^+\) 上の Poisson 点過程の積分として一般化されている．

2.2.2 ジャンプ時刻とジャンプ幅が独立に決まる場合

第 1.6 節で扱ったような，（一様とは限らない）Poisson 点過程の独立付印の場合が特に重要なクラスである．

これは，Lévy 過程のジャンプ測度が，このクラスの複合 Poisson 点過程になるためである．³⁴

命題 (\(\rho_0\)-symmetric compound Poisson process with Lévy measure \(\nu\))³⁵

\(E\times\mathbb{R}^+\) 上の Poisson 点過程 \(\eta\) の強度測度が \(\lambda=\rho_0\otimes\nu\) で表せ，さらに次を満たすとする：

1. \(\rho_0\in\mathcal{P}(E)\) は \(\sigma\)-有限．
2. \(\nu\in\mathcal{P}(\mathbb{R}^+)\) は \[ \int_0^\infty(r\land1)\nu(dr)<\infty \] を満たす．

このとき，次が成り立つ：

1. \(\xi\) は \(\rho_0\)-対称である：\(\rho_0(B)=\rho_0(B')\) ならば，\(\xi(B)\overset{\text{d}}{=}\xi(B')\)．
2. 任意の \(\epsilon>0\) について \(\nu([\epsilon,\infty))<\infty\)．

例（Lévy 過程の跳躍測度）³⁶

Lévy 測度 \(\nu\) を持つ Lévy 過程 \((L_t)\) を考える．

このとき \(\nu\) は，\(\nu(\{0\})=0\) で， \[ \int_\mathbb{R}(1\land\lvert z\rvert^2)\nu(dz)<\infty \] を満たすとされる．

\[ \mathcal{A}_\nu:=\left\{A\in\mathcal{B}(\mathbb{R}\setminus\{0\})\mid \nu(A)<\infty\right\} \] に対して， \[ N([s,t]\times A):=\sum_{s\le r\le t}1_A(\Delta L_r) \] とすると，時刻 \([s,t]\) 間の，幅が \(A\in\mathcal{A}_\nu\) に入るジャンプの数を表す確率変数となる．

これは \(\mathbb{R}_+\times\mathbb{R}\setminus\{0\}\) 上の Poisson 点過程に延長し，強度 \(\ell_+\otimes\nu\) を持つ．

すなわち，\(N\) は Lévy 測度 \(\nu\) を持つ \(\ell_+\)-対称な複合 Poisson 点過程である．この \(N\) を 跳躍測度 (jump measure) ともいう．³⁷

Lévy 測度 \(\nu\) は，単位時間あたり（\(\ell_+\) で測って測度 \(1\) の集合あたり）の平均ジャンプ数を表す： \[ \nu(A)=\operatorname{E}[N([0,1]\times A)]. \]

なお，一般の加法過程（非一様 Lévy 過程）に対しても，同様に跳躍測度は \((\mathbb{R}^d\setminus\{0\})\times\mathbb{R}^+\) 上の Poisson 点過程になる．³⁸

2.3 複合 Poisson 点過程に関する積分

\(E\) 上の複合 Poisson 点過程 \(\xi\) とは，\(E\times\mathbb{R}^+\) 上の Poisson 点過程 \(\eta\) に他ならないため，Poisson 点過程に関する積分を通じて，\(f\in\mathcal{L}(E)\) に関して \[ \int_Ef(z)\,\xi(dz)=\int_Erf(y)\,\eta(dydr) \] と定義できる．³⁹

Campbell の定理 1.3 より，\((r,z)\mapsto rf(z)\) が \(\eta\) の強度測度 \(\lambda\) に関して可積分ならば，右辺は可積分であるから，\((\xi|f)\) も可積分な確率変数を定める．

例（Lévy 過程の Lévy-Itô 分解）⁴⁰

Lévy 過程（一般に加法過程）は，跳躍部分と連続部分との独立和に分解でき，これが Lévy-Itô 分解である．

跳躍部分は，複合 Poisson 点過程 \(\xi\) （跳躍測度）に関する積分として表せる．

しかし，Lévy 測度は \(\mathbb{R}^d\setminus\{0\}\) 上で有限であるのみで，\(0\) の近傍で発散する場合がある．これにより，小さなジャンプを繰り返し，純粋なジャンプの和は発散することがある．そのために，\(0\) の近傍での跳躍部分については，連続部分から項を借りて，中心化された Poisson 積分（第 1.8 節）に関して表示する必要がある．⁴¹

これを実際に見てみよう．\(L\) を特性量 \((\beta,\alpha^2,\nu)\) を持つ Lévy 過程，\(\eta\) を跳躍測度とする．

1. 強度測度 \(\lambda\) について， \[ \int_{\mathbb{R}^d}z\,\lambda(dz) \] は \(0\) の近傍で発散し得るため，単に \[ \int^t_0\int_{\mathbb{R}^d}z\,\eta(dsdz) \] として跳躍部分を表そうとしても，well-defined とは限らない．

2. しかし Lévy 測度は，\(B^d\subset\mathbb{R}^d\) を単位閉球として， \[ \int_{B^d}z^2\,\nu(dz)<\infty \] は満たすから，中心化された Poisson 積分（第 1.8.2 節） \[ \int^t_0\int_{B^d}z\,\widehat{\eta}(dsdz)<\infty \] は定義され，\(\mathcal{L}^2(\operatorname{P})\) の元である：補過程に関する Poisson 積分の等長性より，⁴² \[\begin{align*} \operatorname{E}\left[\left(\int^t_0\int_{B^d}z\,\widehat{\eta}(dsdz)\right)^2\right]&=\int^t_0\int_{B^d}z^2\,dt\lambda(dz)\\ &=t\int_{B^d}z^2\,\lambda(dz)<\infty. \end{align*}\]

3. 一方で \(\mathbb{R}^d\setminus B^d\) 上では， \[ \int_{\mathbb{R}^d\setminus B^d}(z\land1)\,\nu(dz)=\nu(\mathbb{R}^d\setminus B^d)<\infty \] であるから，単に \(\eta\) に関して積分しただけでも，殆ど確実に有限な値を持つ（第 1.8.1 節）．

4. 以上より，任意の Lévy 過程 \(L\) は次の分解として常に表示できる： \[ L_t=\beta t+\alpha B_t+\int^t_0\int_{B^d}z\widehat{\eta}(dsdz)+\int^t_0\int_{\left\{\lvert z\rvert>1\right\}}z\eta(dsdz). \] このとき，\(B\perp\!\!\!\perp N\) であり，最後の項は有限和としても表せる： \[ \int^t_0\int_{\mathbb{R}^d\setminus B^d}zN(dsdz)=\sum_{0\le r\le t}\Delta L_r1_{\mathbb{R}^d\setminus B^d}(\Delta L_r). \] この項が有限であることは，Lévy 測度 \(\nu\) が \(\mathbb{R}^d\setminus B^d\) 上で有限であることによる．

5. 追加で Lévy 測度 \(\nu\) が \[ \int_{B^d}\lvert z\rvert\,\nu(dz)<\infty \] も満たすような Lévy 過程（一般には加法過程）\(L\) については，跳躍部分は \[ L^{\text{jump}}_t:=\int_0^t\int_{\mathbb{R}^d\setminus\{0\}}z\,\eta(dsdz) \] と表せ，\(L-L^{\text{jump}}\) は連続過程で，\(L^{\text{jump}}\) と独立である．⁴³ このような分解ができるとき，\(L^{\text{jump}}\) を 跳躍部分，残りを 連続部分 という．

すなわち，Lévy 過程の中には，無数の小さな跳躍部分が連続部分が相殺しているために収束しているものがあり，そのような場合は明確に跳躍部分と連続部分に分離できないものがある．

例（ショット雑音）⁴⁴

ある \(\widetilde{k}\in\mathcal{L}^1(\ell_d)\) が定める核関数 \[ k(x,y):=\widetilde{k}(x-y) \] と，ある平均を持つ測度 \(\nu\in\mathcal{M}(\mathbb{R})\) が定める強度測度 \(\lambda:=\ell_d\otimes\nu\) を持つ \(\mathbb{R}^d\times\mathbb{R}\) 上の Poisson 点過程 \(\eta\) に関して， \[ Y_x:=\int_{\mathbb{R}^{d}\times\mathbb{R}}r\widetilde{k}(x-y)\eta(dydr) \] で定まる確率場 \(\{Y_x\}_{x\in\mathbb{R}^d}\) を，Poisson 過程 \(\eta\) が駆動する ショット雑音 という．

2.4 複合 Poisson 計数過程の定義

単に複合 Poisson 過程といった場合，通常，ここでいう一様な複合 Poisson 計数過程を指すことが多い．

2.4.1 一様な場合

定義 (compound Poisson processes)⁴⁵

\(\lambda>0\) を正数，\(\mu\in\mathcal{P}(\mathbb{R}^d)\) を確率分布とする．一様な 複合 Poisson 過程 \(\mathrm{CP}(\lambda,\mu)\) とは，強度 \(\lambda\) を持つ（一様な） Poisson 過程 \(N\) が定める Lévy 過程 \(\{X_t\}\subset\mathcal{L}(\Omega;\mathbb{R}^d)\) をいう： \[ X_t:=\sum_{n=1}^{N_t}Y_n, \] \[ Y_n\overset{\text{i.i.d.}}{\sim}\mu. \]

この \(X_t\) は Lévy 過程になっており，\(X_t\) の特性関数は \[ \varphi(u)=\exp\left(\lambda t\int_{\mathbb{R}^d}\biggr(e^{i(u|y)}-1\biggl)\mu(dy)\right) \] で表される．⁴⁶ すなわち，\(X_t\) は複合 Poisson 分布 \(\mathrm{CP}(\lambda t,\mu)\) に従う．

2.4.2 非一様・非有限な場合

すなわち，複合 Poisson 分布が一様であるとは，背後にある \(\mathbb{R}^d\times\mathbb{R}_+\) 上の Poisson 点過程が，\(\mathbb{R}_+\) 上の一様な Poisson 点過程（第 1.5.2 節）の独立付印過程になっていることをいう（第 1.6 節）．

さらに，Lévy 測度が \(\lambda\mu\) という有限測度になるという重要な仮定も含まれている．

一方で，一般の Lévy 分布の跳躍測度は，\(\mathbb{R}_+\) 上の一様な Poisson 点過程に基づくとは限らない（第 2.2.2 節）上に，\(\mathbb{R}^d\setminus\{0\}\) 上有限とも限らない．

このような場合でも，一般の複合 Poisson 点過程 \(\xi\) を通じて，複合 Poisson 計数過程が \[ M_t(\omega):=\xi(\omega,[0,t]) \] と定義できる．

\(\xi\) が \(\mathbb{R}_+\times\mathbb{R}^d\) 上の Poisson 点過程 \(\eta\) が定めるものであるとすると， \[ M_t(\omega)=\int_0^t\int_{\mathbb{R}^d\setminus\{0\}}r\,\eta(\omega,dsdr) \] と表せる．

2.5 シミュレーション

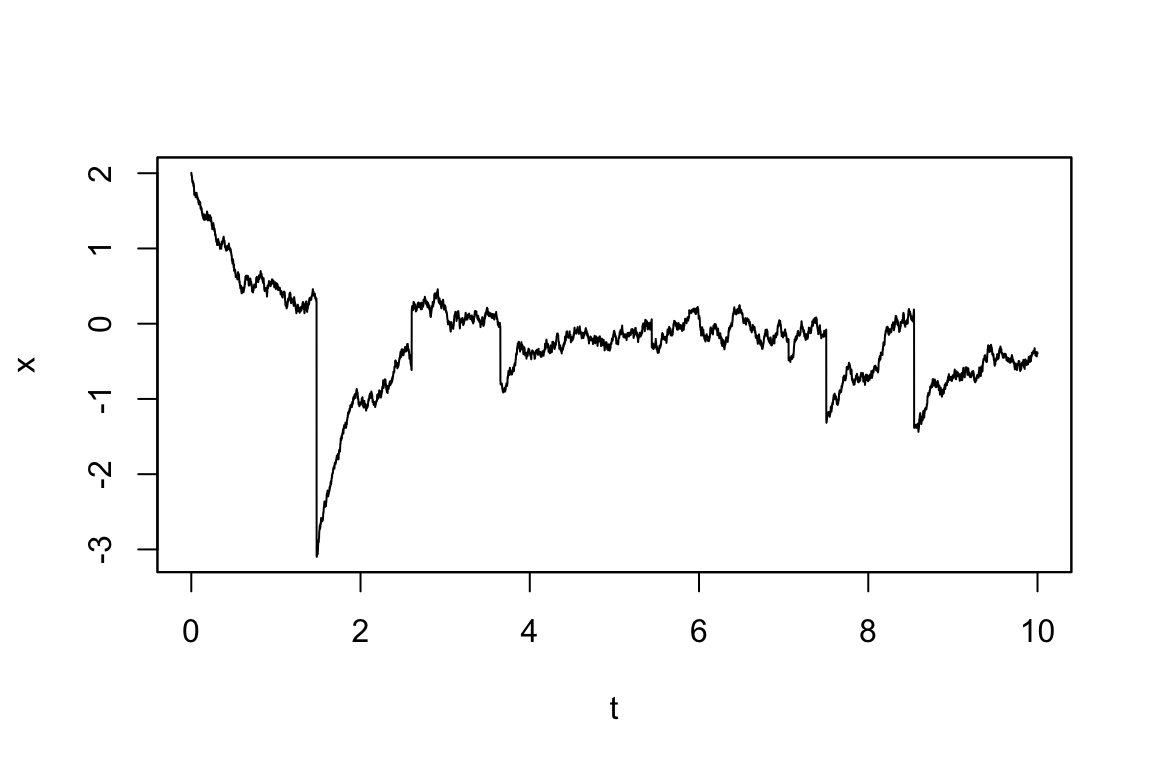
2.5.1 複合 Poisson 過程のシミュレーション

yuimaパッケージには，複合 Poisson 分布専用のコンストラクタsetPoissonが用意されている．このコンストラクタは２つの引数を持つ：

setPoissonの引数⁴⁷

• intensity：強度（関数） \(\lambda>0\) として用いる変数名を文字列で指定する．
• df：跳躍測度 \(\mu\in\mathcal{P}(\mathbb{R}^d)\) として用いる分布名を，文字列のリストで指定する．
• scale=1：\(\|\nu\|_\mathrm{TV}\) の値のこと．
• dimension=1：\(d\) の値．

例（一様 Poisson 過程の例）⁴⁸

Poisson 過程はジャンプの大きさが定数１の複合 Poisson 過程であるから，dfとしては \(\delta_1\) を意味するdconst(z,1)を指定する．

library(yuima)

mod1 <- setPoisson(intensity="lambda", df=list("dconst(z,1)"))

Terminal <- 30
samp <- setSampling(Terminal=Terminal, n=3000)
set.seed(123)
poisson1 <- simulate(mod1, true.par=list(lambda=1), sampling=samp)

plot(poisson1)

例（正規分布に従う跳躍を持つ複合 Poisson 過程）⁴⁹

dfとして正規分布族dnorm(z,mu,sigma)を指定すれば良い．

mod2 <- setPoisson(intensity="lambda", df=list("dnorm(z,mu,sigma)"))
poisson2 <- simulate(mod2, sampling=samp, true.par=list(lambda=1, mu=0, sigma=2))

跳躍分布が \(\mu=\operatorname{N}_1(0,2)\) である場合の複合 Poisson 過程をシミュレーションは次のとおり：

plot(poisson2)

2.5.2 複合 Poisson 過程が駆動する Lévy 過程のシミュレーション

この場合はsetModel内でモデルを定義する．

setModelの引数⁵⁰

• jump.coeff：\(dM_t\) 項の係数を，文字列のベクトルで指定する．
• measure.type：CPと指定することで，measure引数が複合 Poisson 過程 \(M\) に付随する Poisson 点過程 \(\eta\) の強度測度と解釈される．
• measure：\(\eta\) の強度測度 \(\lambda\otimes\nu\) を，intensityとdfのリストとして指定する．

例（複合 Poisson 跳躍を持つ Lévy 過程）⁵¹

複合 Poisson 過程 \(M\sim\mathrm{CP}(\lambda,\operatorname{N}(2,0.1))\) が定める SDE \[ dX_t=-\theta X_tdt+\sigma dB_t+\left(\gamma+\frac{X_{t-}}{\sqrt{1+X^2_{t-}}}\right)dM_t \] \[ X_0=0 \] は次のように定義する：

modJump <- setModel(drift = c("-theta*x"), diffusion = "sigma", jump.coeff=c("gamma+x/sqrt(1+x^2)"), measure = list(intensity="lambda", df=list("dnorm(z, -3, 1)")), measure.type="CP", solve.variable="x")

samp <- setSampling(n=10000,Terminal=10)

X <- simulate(modJump, xinit=2, sampling=samp, true.par= list(theta=2, sigma=0.5,gamma=0.3,lambda=0.5))
plot(X)

References

Applebaum, D. (2009). Lévy processes and stochastic calculus,Vol. 116. Cambridge University Press.

Baudoin, F. (2014). Diffusion processes and stochastic calculus,Vol. 16. European Mathematical Society.

Brémaud, P. (1981). Point Processes and Queues: Martingale Dynamics. Springer-Verlag Berlin Heidelberg New York.

Campbell, N. (1909). The study of discontinuous phenomena. Proc Cambr. Phil. Soc, vol. 15, pp. 117–136.

Chopin, N., and Papaspiliopoulos, O. (2020). An introduction to sequential monte carlo. Springer Cham.

Cox, D. R. (1955). Some statistical methods connected with series of events. Journal of the Royal Statistical Society: Series B (Methodological), 17(2), 129–157.

Eberle, A. (2012). Stochastic analysis.

Iacus, S. M., and Yoshida, N. (2018). Simulation and inference for stochastic processes with YUIMA: A comprehensive r framework for SDEs and other stochastic processes. Springer Cham.

Kallenberg, O. (2017). Random measures, theory and applications,Vol. 77. Springer Cham.

Kingman, J. F. C. (1992). Poisson processes. Clarendon Press.

Kingman, J. F. C. (2006). Poisson Processes Revisited. Probability and Mathematical Statistics, 26(1), 77–95.

Lewis, P. A. W., and Shedler, G. S. (1979). Simulation of nonhomogeneous poisson processes by thinning. Naval Research Logistics Quarterly, 26(3), 403–413.

Mitov, K. V., and Omey, E. (2014). Renewal processes. Springer Cham.

Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. MIT Press.

Nualart, D., and Nualart, E. (2018). Introduction to malliavin calculus,Vol. 8. Cambridge University Press.

Nummelin, E. (1984). General Irreducible Markov Chains and Non-Negative Operators,Vol. 83. Cambridge University Press.

Ogata, Y. (1981). On lewis’ simulation method for point processes. IEEE Transactions on Information Theory, 27(1), 23–31.

Protter, P. E. (2005). Stochastic integration and differential equations,Vol. 2. Springer Berlin, Heidelberg.

Resnick, S. I. (2002). Adventures in stochastic processes. Birkhäuser Boston.

Revuz, D., and Yor, M. (1999). Continuous martingales and brownian motion. Springer Berlin, Heidelberg.

Sato, K. (2013). Lévy processes and infinitely divisible distributions. Cambridge University Press.

Shibue, F., Ryohei AND Komaki. (2020). Deconvolution of calcium imaging data using marked point processes. PLOS Computational Biology, 16(3), 1–25.

Shibue, R., and Komaki, F. (2017). Firing rate estimation using infinite mixture models and its application to neural decoding. Journal of Neurophysiology, 118(5), 2902–2913. doi: 10.1152/jn.00818.2016.

Todorovic, P., and Yevjevich, V. (1969). Stochastic process of precipitation. Hydrology Papers. Colorado State University.

Vasdekis, G. (2021). On zig-zag extensions and related ergodicity properties (PhD thesis). University of Warwick. Retrieved from http://webcat.warwick.ac.uk/record=b3714913

伊藤清. (1991). 確率論. 岩波書店.

西村克己, and 江藤剛治. (1981). Marked point Processモデルによる降水量時系列の解析. 水理講演会論文集, 25, 191–196.

Footnotes

1. (Nualart and Nualart, 2018, p. 159) 例9.1.3，(Revuz and Yor, 1999, p. 471) 定義XII.1.3 などは，Poisson 計数過程の方を Poisson 過程と呼んでおり，(Last_Penrose2017?) などは Poisson 点過程の方を Poisson 過程と呼んでいる．(Eberle, 2012, p. 18) では，ここでは点過程とランダム測度を混用しているが，この２つを使い分けている．(Vasdekis, 2021) も，ここでいう計数過程を点過程と呼んでいる．

2. (Revuz and Yor, 1999, p. 472) 命題XII.1.4など．

3. (Kallenberg, 2017, p. 49)，(Last_Penrose2017?) 定義2.1 に倣った．全く同じ概念を (伊藤清, 1991, p. 298) は 偶然配置 と呼ぶ．

4. (Last_Penrose2017?) 系6.5 を参照．

5. (Last_Penrose2017?) 定義13.5 に倣った．

6. (Murphy, 2023, p. 696) 18.4.3 節も参照．

7. (伊藤清, 1991, p. 298) に倣った．

8. (Last_Penrose2017?) 命題2.7 に倣った．(Campbell, 1909) は元々真空管内の shot noise の研究をしていた．結果の一部は G. H. Hardy にもよるという．

9. (Nualart and Nualart, 2018, p. 160) 定義9.2.1，(Sato, 2013, p. 119) 第4章19節，(Resnick, 2002, p. 303)，(Sato, 2013, p. 119) 定義19.1，(Last_Penrose2017?) 定義3.1 に倣った．

10. (Revuz and Yor, 1999, p. 476) 命題 XII.1.12，(Last_Penrose2017?) 命題3.2 はより一般的な状況で示している．

11. (Nualart and Nualart, 2018, p. 160) 定理9.2.2 では，\(\lambda\) はアトムを持たないとし，\(E\) を Polish 空間として示している．(Last_Penrose2017?) 系3.7 はここよりも一般的な設定で示している．

12. (Eberle, 2012, p. 19) 定理1.6も参照．

13. 逆に，指数分布のシミュレーションにより，一様分布の順序統計量が効率的にシミュレーションできる．このことは粒子フィルターにおけるリサンプリングに応用できる．(Chopin and Papaspiliopoulos, 2020, p. 113) 命題9.1も参照．

14. \(\pi=\delta_m\) であるとき，\(\eta\) を単に二項（点）過程という．これは \(\eta(B)\sim\mathrm{Bin}(m,\mu(B))\) が成り立つためである．(Last_Penrose2017?) 定義3.4も参照．

15. (Last_Penrose2017?) 命題3.8も参照．

16. (Last_Penrose2017?) 定理7.2参照．

17. (Last_Penrose2017?) 定義5.3 に倣った．(Kingman, 1992, p. 55) 5.2節や (Brémaud, 1981, p. 233) も参照．

18. 例えば (Kingman, 1992, p. 55)，(Last_Penrose2017?) 命題5.5 を参照．

19. 日本語文献としては，(西村克己 and 江藤剛治, 1981) も参照．

20. (Last_Penrose2017?) 定義5.7 に従った．

21. (Last_Penrose2017?) 系5.9 参照．

22. (Last_Penrose2017?) 命題12.1 参考．

23. (Nualart and Nualart, 2018, p. 163) 9.3節，(Last_Penrose2017?) 命題12.4 など．

24. (Sato, 2013, p. 123) 定理19.5 や (Eberle, 2012, p. 20) 定理1.7 は強度測度 \(\lambda\) が有限な場合について述べている，(Nualart and Nualart, 2018, p. 164) は補過程に関する積分に関して述べており，そのために追加で\(-iu\int_Eh(z)\lambda(dz)\) の項を持つ．．

25. (Nualart and Nualart, 2018, p. 159) 例9.1.4，(Last_Penrose2017?) 例15.5 など．

26. (Applebaum, 2009, p. 50) も参照．

27. (Iacus and Yoshida, 2018, p. 171) 4.8.1 節も参照．

28. (Resnick, 2002, p. 174)，(Mitov and Omey, 2014, p. 1)，(Nummelin, 1984, p. 49) 定義4.2 などに倣った．

29. (Nualart and Nualart, 2018, pp. 159–160) も参照．

30. \(\left\{z\in\mathbb{R}^d\mid\lvert z\rvert>\epsilon\right\}\) 上で有限でないと，これを Lévy 測度にもつ Lévy 過程は存在しない．(Eberle, 2012, p. 20) 定理1.7も参照．

31. (Eberle, 2012, p. 26) 定理1.10 も参照．

32. (Kingman, 1992, p. 79) 第８章，(Last_Penrose2017?) 第 15.3 節参照．

33. (Last_Penrose2017?) に倣った．

34. 一様じゃない Lévy 過程，すなわち加法過程の場合は，\(\lambda((0,t]\times B)=\nu_t(B)\) という関係にある．これはもはや独立付印ではないが，やはり印付きの Poisson 過程が肝心であることは変わらない．

35. (Last_Penrose2017?) も参照，

36. (Nualart and Nualart, 2018, p. 162) 例9.2.4 を参考．

37. (Nualart and Nualart, 2018, p. 162) 例9.2.4 による用語法．\(N\) をランダム測度として跳躍測度と呼んでいる．

38. (Sato, 2013, p. 120) 定理19.2(i) を参照．

39. (Nualart and Nualart, 2018, p. 164) 例9.3.1，(Last_Penrose2017?) 15.4節なども参照．

40. (Nualart and Nualart, 2018, p. 164) 例9.3.1，(Sato, 2013, p. 120) 定理19.2，(Protter, 2005, p. 31) 定理42 など参照．

41. (Sato, 2013, p. 119) が指摘するように，まるで Cauchy の主値積分である．

42. ただし，\(\widehat{\eta}([0,t]\times A):=\eta([0,t]\times A)-t\nu(A)\) を中心化した Poisson 過程とした．これを Poisson 補過程 (compensated Poisson process) ともいう．

43. (Sato, 2013, p. 121) 定理19.3 も参照．

44. (Last_Penrose2017?) 例15.14 を参考にした．

45. (Iacus and Yoshida, 2018, p. 137), p.158，(Sato, 2013, p. 18) 定理4.3，(Protter, 2005, p. 33) 例2，(Baudoin, 2014, p. 90) 演習3.44，(Applebaum, 2009, p. 49) 命題1.3.11 に倣った．

46. (Sato, 2013, p. 20) 命題4.5など参照．

47. (Iacus and Yoshida, 2018, p. 137) 参照．

48. (Iacus and Yoshida, 2018, pp. 137–138) も参照．

49. (Iacus and Yoshida, 2018, p. 139) も参照．

50. Lévy 過程が駆動する SDE モデルの定義方法は (Iacus and Yoshida, 2018, p. 191) 4.11.3 節を参照．

51. (Iacus and Yoshida, 2018, p. 191) 参照．