ニューラル常微分方程式

PyTorch によるハンズオン

Deep
Sampling
Python
Author

司馬博文

Published

8/20/2024

概要
Gauss 分布からデータ分布までの変換を，可逆なニューラルネットワークでモデリングする正規化流は，ODE に基づいて設計することもできる．この方法は Neural ODE や連続な正規化流 (CNF) ともいう．今回は PyTorch を用いて，正規化流の実装の概要を見る．

関連ページ

1 事前準備

Code 
import math
import numpy as np
from IPython.display import clear_output
from tqdm import tqdm_notebook as tqdm

import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.color_palette("bright")
import matplotlib as mpl
import matplotlib.cm as cm

import torch
from torch import Tensor
from torch import nn
from torch.nn  import functional as F
from torch.autograd import Variable

use_cuda = torch.cuda.is_available()

まずは ODE ソルバーを用意する．これはどのようなものでも NODE のサブルーチンとして使うことができる．

def ode_solve(z0, t0, t1, f):
    """
    Simplest Euler ODE initial value solver
    """
    h_max = 0.05
    n_steps = math.ceil((abs(t1 - t0)/h_max).max().item())

    h = (t1 - t0)/n_steps
    t = t0
    z = z0

    for i_step in range(n_steps):
        z = z + h * f(z, t)
        t = t + h
    return z

NODE では，\(D_{x}L_t\) と \(D_\theta L_t\) とは随伴状態 \(a(t)\) に関する ODE で得られる．

この ODE の係数を事前に自動微分を通じて計算しておくための親クラスを定義する：

class ODEF(nn.Module):
    def forward_with_grad(self, z, t, grad_outputs):
        """Compute f and a df/dz, a df/dp, a df/dt"""
        batch_size = z.shape[0]

        out = self.forward(z, t)

        a = grad_outputs
        adfdz, adfdt, *adfdp = torch.autograd.grad(
            (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a),
            allow_unused=True, retain_graph=True
        )
        # grad method automatically sums gradients for batch items, we have to expand them back
        if adfdp is not None:
            adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0)
            adfdp = adfdp.expand(batch_size, -1) / batch_size
        if adfdt is not None:
            adfdt = adfdt.expand(batch_size, 1) / batch_size
        return out, adfdz, adfdt, adfdp

    def flatten_parameters(self):
        p_shapes = []
        flat_parameters = []
        for p in self.parameters():
            p_shapes.append(p.size())
            flat_parameters.append(p.flatten())
        return torch.cat(flat_parameters)

2 Neural ODE の実装

Neural ODE では誤差逆伝播の代わりに随伴感度法を用いる．

これは torch.nn.Module を継承したクラスとしては定義できないため，torch.autograd.Function を継承したクラスとして定義する：

class ODEAdjoint(torch.autograd.Function):
    @staticmethod
    def forward(ctx, z0, t, flat_parameters, func):
        assert isinstance(func, ODEF)
        bs, *z_shape = z0.size()
        time_len = t.size(0)

        with torch.no_grad():
            z = torch.zeros(time_len, bs, *z_shape).to(z0)
            z[0] = z0
            for i_t in range(time_len - 1):
                z0 = ode_solve(z0, t[i_t], t[i_t+1], func)
                z[i_t+1] = z0

        ctx.func = func
        ctx.save_for_backward(t, z.clone(), flat_parameters)
        return z

    @staticmethod
    def backward(ctx, dLdz):
        """
        dLdz shape: time_len, batch_size, *z_shape
        """
        func = ctx.func
        t, z, flat_parameters = ctx.saved_tensors
        time_len, bs, *z_shape = z.size()
        n_dim = np.prod(z_shape)
        n_params = flat_parameters.size(0)

        # Dynamics of augmented system to be calculated backwards in time
        def augmented_dynamics(aug_z_i, t_i):
            """
            tensors here are temporal slices
            t_i - is tensor with size: bs, 1
            aug_z_i - is tensor with size: bs, n_dim*2 + n_params + 1
            """
            z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim]  # ignore parameters and time

            # Unflatten z and a
            z_i = z_i.view(bs, *z_shape)
            a = a.view(bs, *z_shape)
            with torch.set_grad_enabled(True):
                t_i = t_i.detach().requires_grad_(True)
                z_i = z_i.detach().requires_grad_(True)
                func_eval, adfdz, adfdt, adfdp = func.forward_with_grad(z_i, t_i, grad_outputs=a)  # bs, *z_shape
                adfdz = adfdz.to(z_i) if adfdz is not None else torch.zeros(bs, *z_shape).to(z_i)
                adfdp = adfdp.to(z_i) if adfdp is not None else torch.zeros(bs, n_params).to(z_i)
                adfdt = adfdt.to(z_i) if adfdt is not None else torch.zeros(bs, 1).to(z_i)

            # Flatten f and adfdz
            func_eval = func_eval.view(bs, n_dim)
            adfdz = adfdz.view(bs, n_dim)
            return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1)

        dLdz = dLdz.view(time_len, bs, n_dim)  # flatten dLdz for convenience
        with torch.no_grad():
            ## Create placeholders for output gradients
            # Prev computed backwards adjoints to be adjusted by direct gradients
            adj_z = torch.zeros(bs, n_dim).to(dLdz)
            adj_p = torch.zeros(bs, n_params).to(dLdz)
            # In contrast to z and p we need to return gradients for all times
            adj_t = torch.zeros(time_len, bs, 1).to(dLdz)

            for i_t in range(time_len-1, 0, -1):
                z_i = z[i_t]
                t_i = t[i_t]
                f_i = func(z_i, t_i).view(bs, n_dim)

                # Compute direct gradients
                dLdz_i = dLdz[i_t]
                dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0]

                # Adjusting adjoints with direct gradients
                adj_z += dLdz_i
                adj_t[i_t] = adj_t[i_t] - dLdt_i

                # Pack augmented variable
                aug_z = torch.cat((z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z), adj_t[i_t]), dim=-1)

                # Solve augmented system backwards
                aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics)

                # Unpack solved backwards augmented system
                adj_z[:] = aug_ans[:, n_dim:2*n_dim]
                adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params]
                adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:]

                del aug_z, aug_ans

            ## Adjust 0 time adjoint with direct gradients
            # Compute direct gradients
            dLdz_0 = dLdz[0]
            dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0]

            # Adjust adjoints
            adj_z += dLdz_0
            adj_t[0] = adj_t[0] - dLdt_0
        return adj_z.view(bs, *z_shape), adj_t, adj_p, None

これを nn.Module クラスとしてラップすることで，準備完了である：

class NeuralODE(nn.Module):
    def __init__(self, func):
        super(NeuralODE, self).__init__()
        assert isinstance(func, ODEF)
        self.func = func

    def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False):
        t = t.to(z0)
        z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func)
        if return_whole_sequence:
            return z
        else:
            return z[-1]

3 ダイナミクスの再現

3.1 線型ダイナミクス

簡単な線型ダイナミクスを，線型なダイナミクスで学習する．

class LinearODEF(ODEF):
    def __init__(self, W):
        super(LinearODEF, self).__init__()
        self.lin = nn.Linear(2, 2, bias=False)
        self.lin.weight = nn.Parameter(W)

    def forward(self, x, t):
        return self.lin(x)

class SpiralFunctionExample(LinearODEF):
    def __init__(self):
        super(SpiralFunctionExample, self).__init__(Tensor([[-0.1, -1.], [1., -0.1]]))

class RandomLinearODEF(LinearODEF):
    def __init__(self):
        # super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)
        super(RandomLinearODEF, self).__init__(Tensor([[0.1, -0.1], [0.1, -0.1]]))

def to_np(x):
    return x.detach().cpu().numpy()
def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)):
    plt.figure(figsize=figsize)
    if obs is not None:
        if times is None:
            times = [None] * len(obs)
        for o, t in zip(obs, times):
            o, t = to_np(o), to_np(t)
            for b_i in range(o.shape[1]):
                plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma)

    if trajs is not None:
        for z in trajs:
            z = to_np(z)
            plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5)
        if save is not None:
            plt.savefig(save)
    plt.show()

def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10, lr=0.01):
    # Create data
    z0 = Variable(torch.Tensor([[0.6, 0.3]]))

    t_max = 6.29*5
    n_points = 200

    index_np = np.arange(0, n_points, 1, dtype=np.int64)
    index_np = np.hstack([index_np[:, None]])
    times_np = np.linspace(0, t_max, num=n_points)
    times_np = np.hstack([times_np[:, None]])

    times = torch.from_numpy(times_np[:, :, None]).to(z0)
    obs = ode_true(z0, times, return_whole_sequence=True).detach()
    obs = obs + torch.randn_like(obs) * 0.01

    # Get trajectory of random timespan
    min_delta_time = 1.0
    max_delta_time = 5.0
    max_points_num = 32
    def create_batch():
        t0 = np.random.uniform(0, t_max - max_delta_time)
        t1 = t0 + np.random.uniform(min_delta_time, max_delta_time)

        idx = sorted(np.random.permutation(index_np[(times_np > t0) & (times_np < t1)])[:max_points_num])

        obs_ = obs[idx]
        ts_ = times[idx]
        return obs_, ts_

    # Train Neural ODE
    optimizer = torch.optim.Adam(ode_trained.parameters(), lr=lr)
    for i in range(n_steps):
        obs_, ts_ = create_batch()

        z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True)
        loss = F.mse_loss(z_, obs_.detach())

        optimizer.zero_grad()
        loss.backward(retain_graph=True)
        optimizer.step()

        if i % plot_freq == 0:
            z_p = ode_trained(z0, times, return_whole_sequence=True)

            plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"Files/{name}/{i//plot_freq}.png")
            clear_output(wait=True)
ode_true = NeuralODE(SpiralFunctionExample())
ode_trained = NeuralODE(RandomLinearODEF())
conduct_experiment(ode_true, ode_trained, 500, "linear")

ImageMagick により git 生成した結果は次の通り：

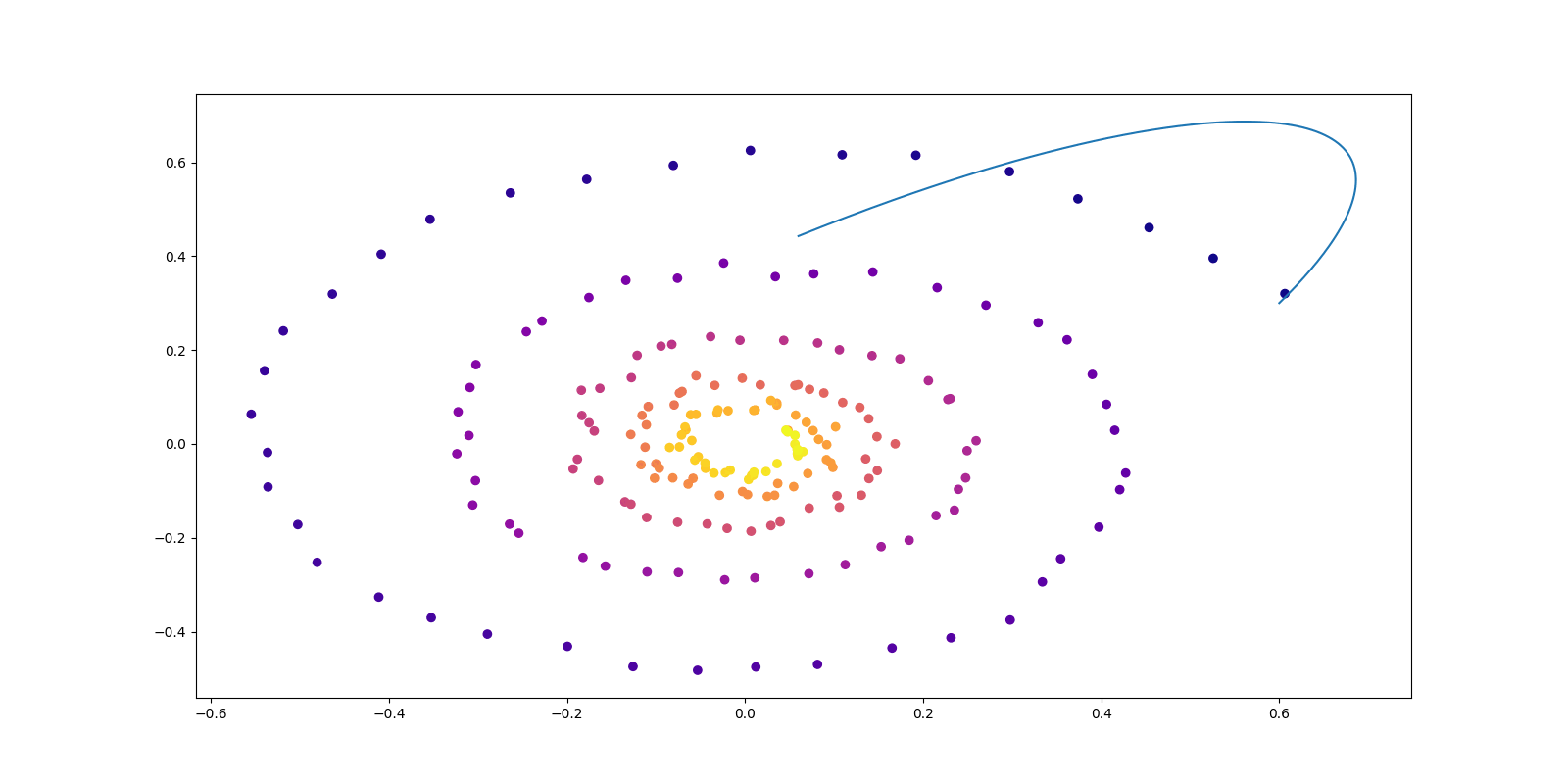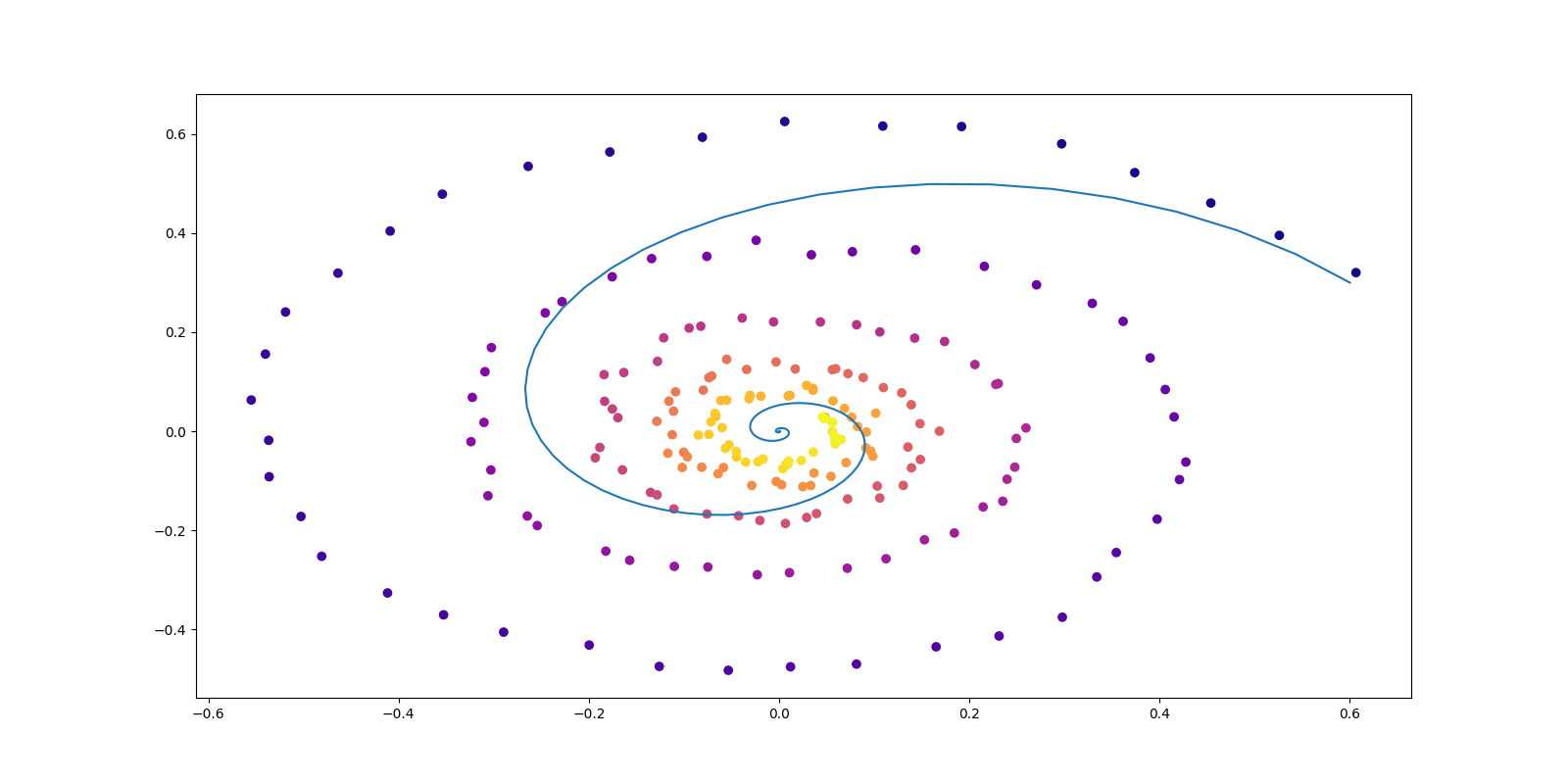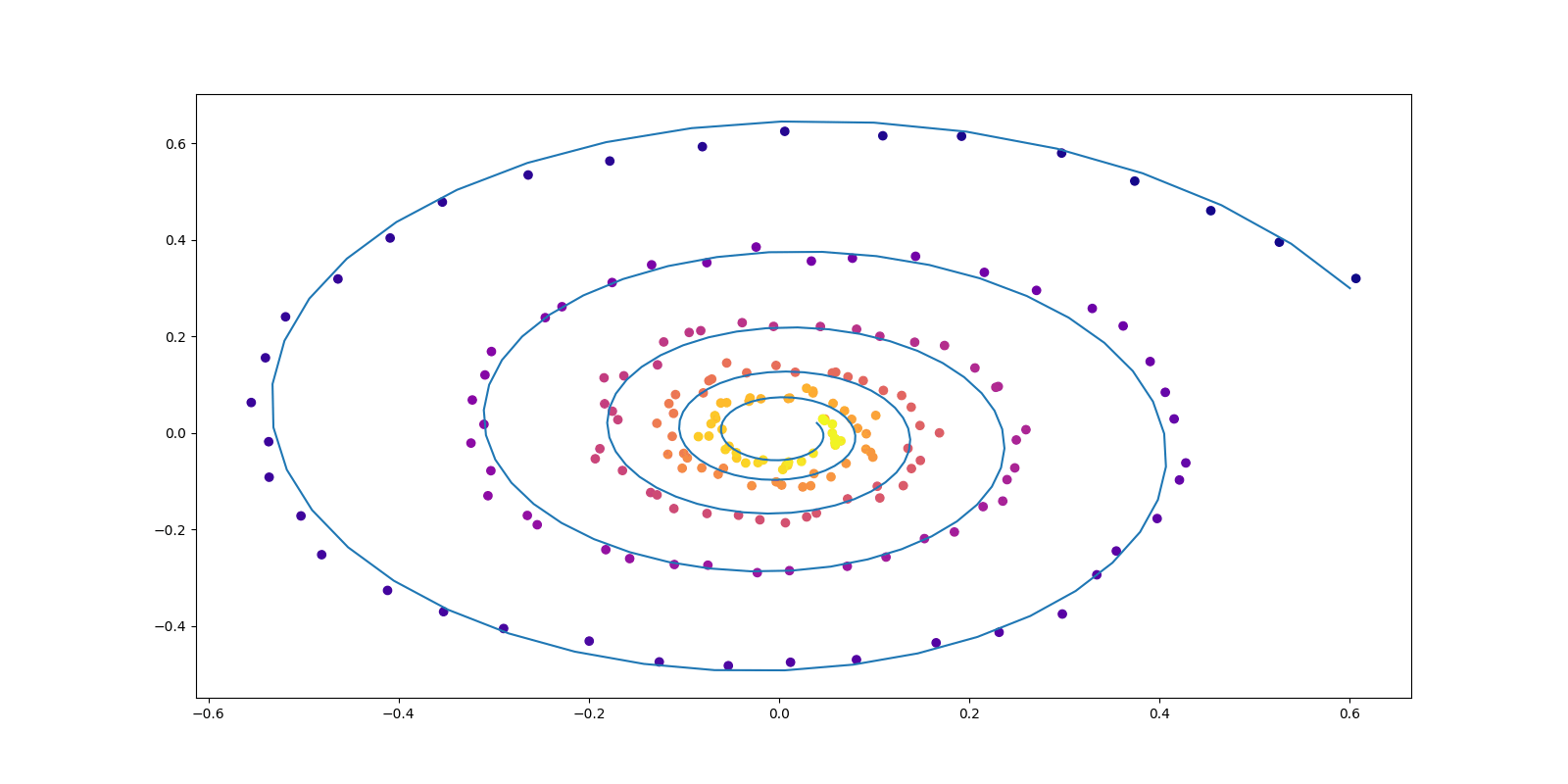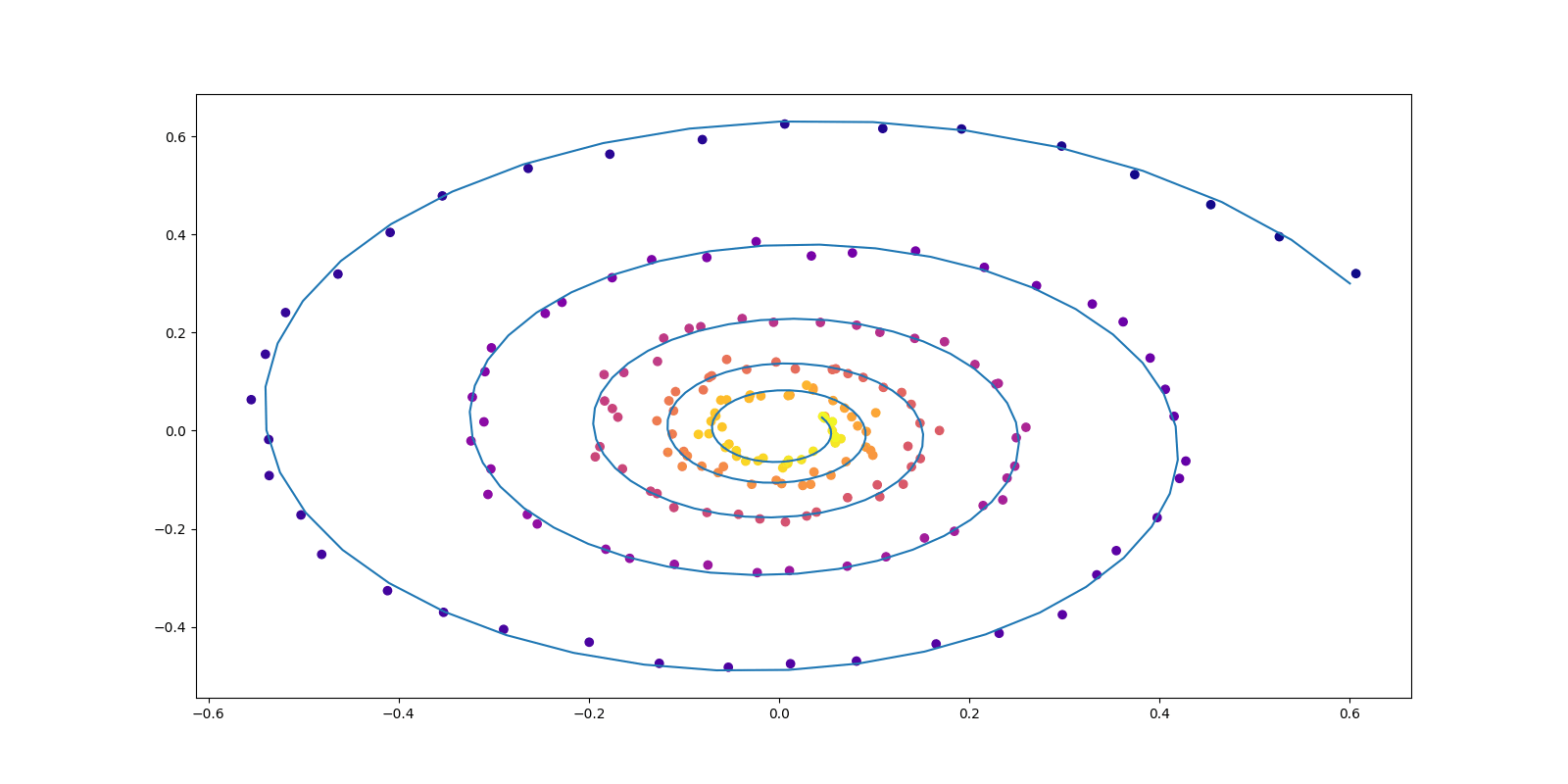
convert -delay 10 -loop 0 $(for i in {0..49}; do echo $i.png; done) output.gif

3.2 非線型ダイナミクス

今回は非線型のダイナミクスを，ELU を備えた一層のニューラルネットワークで学習する：

class TestODEF(ODEF):
    def __init__(self, A, B, x0):
        super(TestODEF, self).__init__()
        self.A = nn.Linear(2, 2, bias=False)
        self.A.weight = nn.Parameter(A)
        self.B = nn.Linear(2, 2, bias=False)
        self.B.weight = nn.Parameter(B)
        self.x0 = nn.Parameter(x0)

    def forward(self, x, t):
        xTx0 = torch.sum(x*self.x0, dim=1)
        dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0)
        return dxdt

class NNODEF(ODEF):
    def __init__(self, in_dim, hid_dim, time_invariant=False):
        super(NNODEF, self).__init__()
        self.time_invariant = time_invariant

        if time_invariant:
            self.lin1 = nn.Linear(in_dim, hid_dim)
        else:
            self.lin1 = nn.Linear(in_dim+1, hid_dim)
        self.lin2 = nn.Linear(hid_dim, hid_dim)
        self.lin3 = nn.Linear(hid_dim, in_dim)
        self.elu = nn.ELU(inplace=True)

    def forward(self, x, t):
        if not self.time_invariant:
            x = torch.cat((x, t), dim=-1)

        h = self.elu(self.lin1(x))
        h = self.elu(self.lin2(h))
        out = self.lin3(h)
        return out
func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]]))
ode_true = NeuralODE(func)

func = NNODEF(2, 16, time_invariant=True)
ode_trained = NeuralODE(func)

conduct_experiment(ode_true, ode_trained, 3000, "nonlinear", plot_freq=30, lr=0.001)

逡巡を繰り返して学習する様子がよく伺える．学習率を lr=0.001 としているが，lr=0.01 でも lr=0.005 でも，学習が非常に良い線まで行ってもすぐに初期値よりもカオスなダイナミクスに戻ってしまう挙動がよく見られた．

4 文献紹介

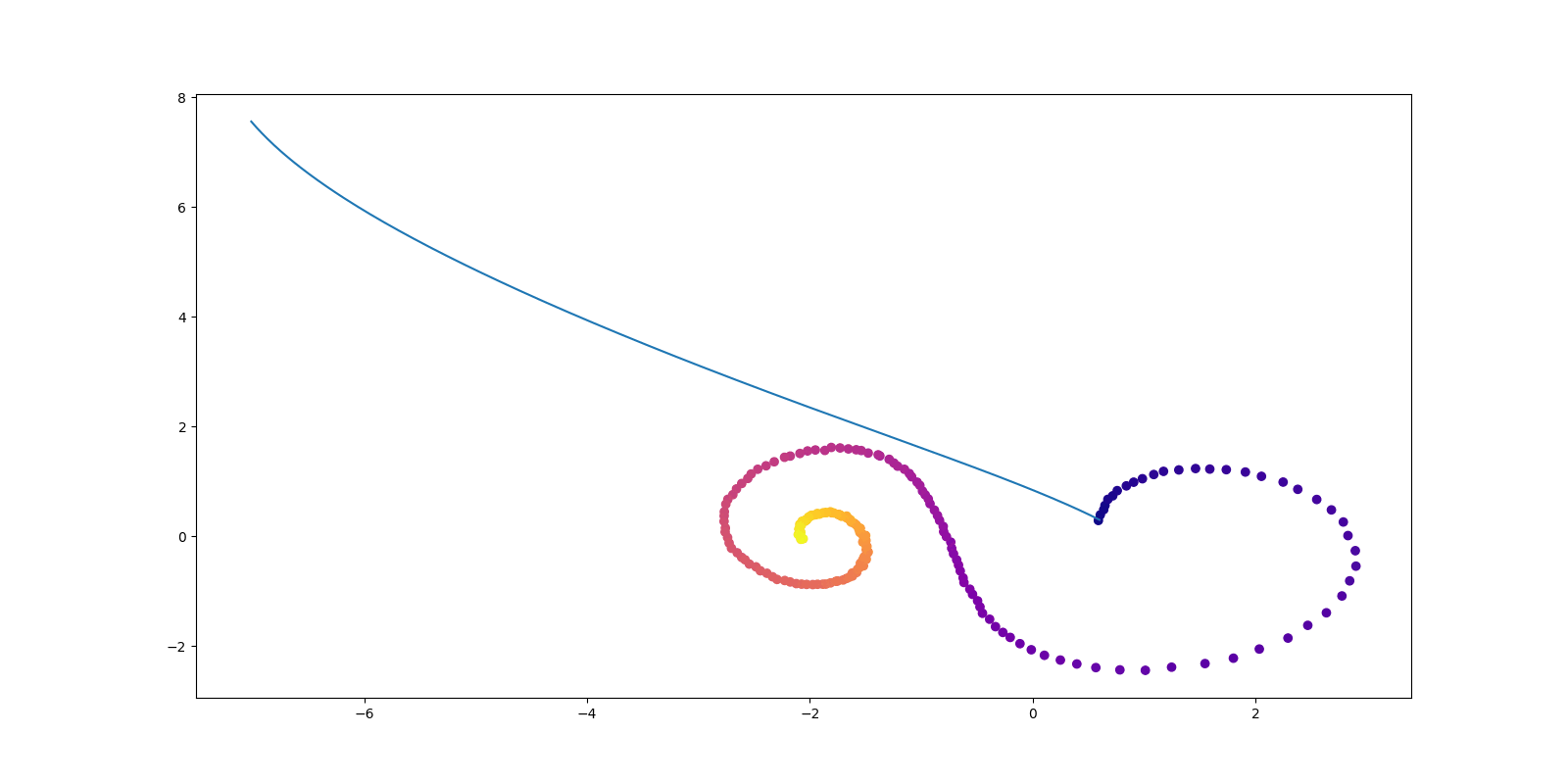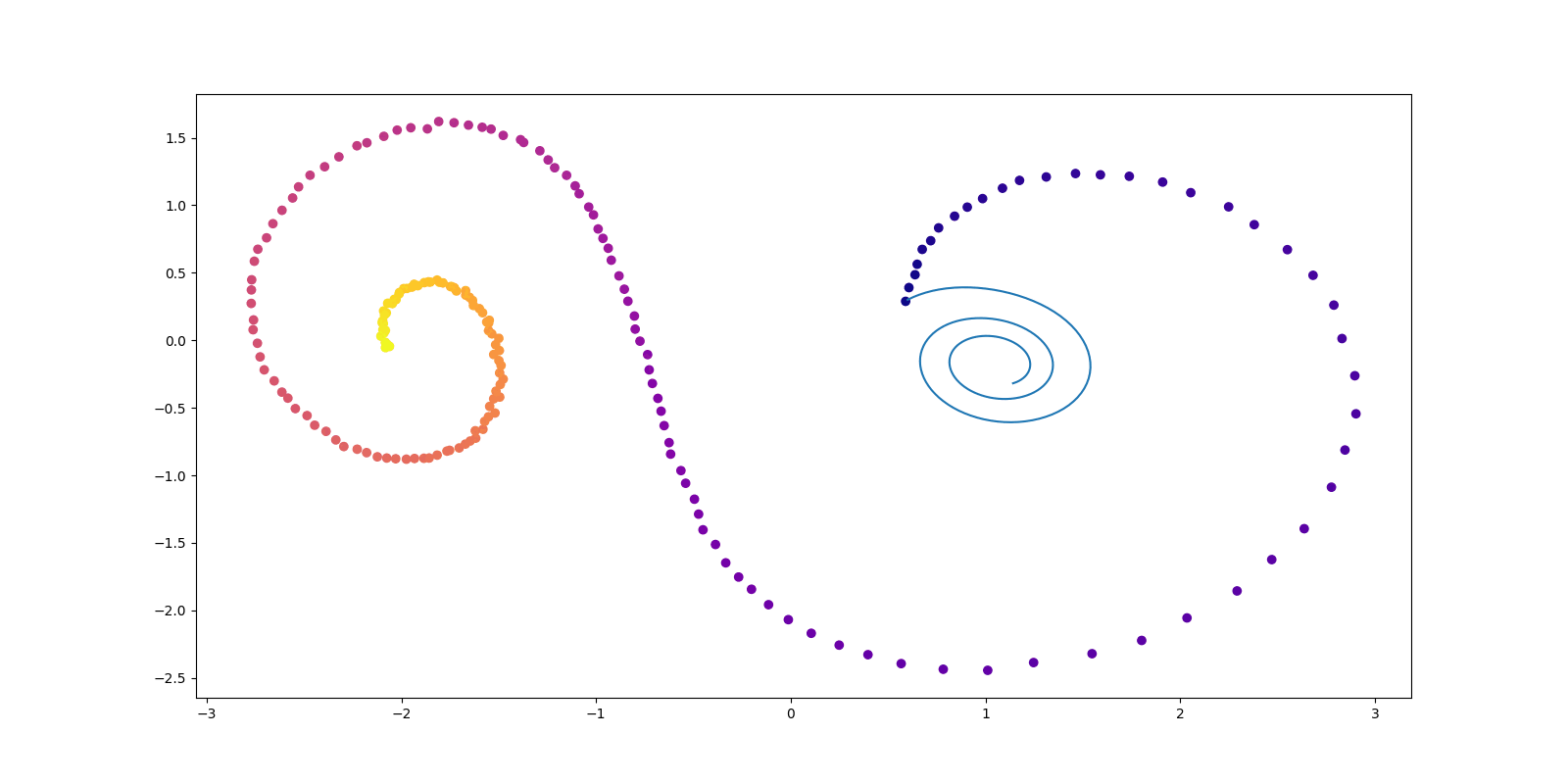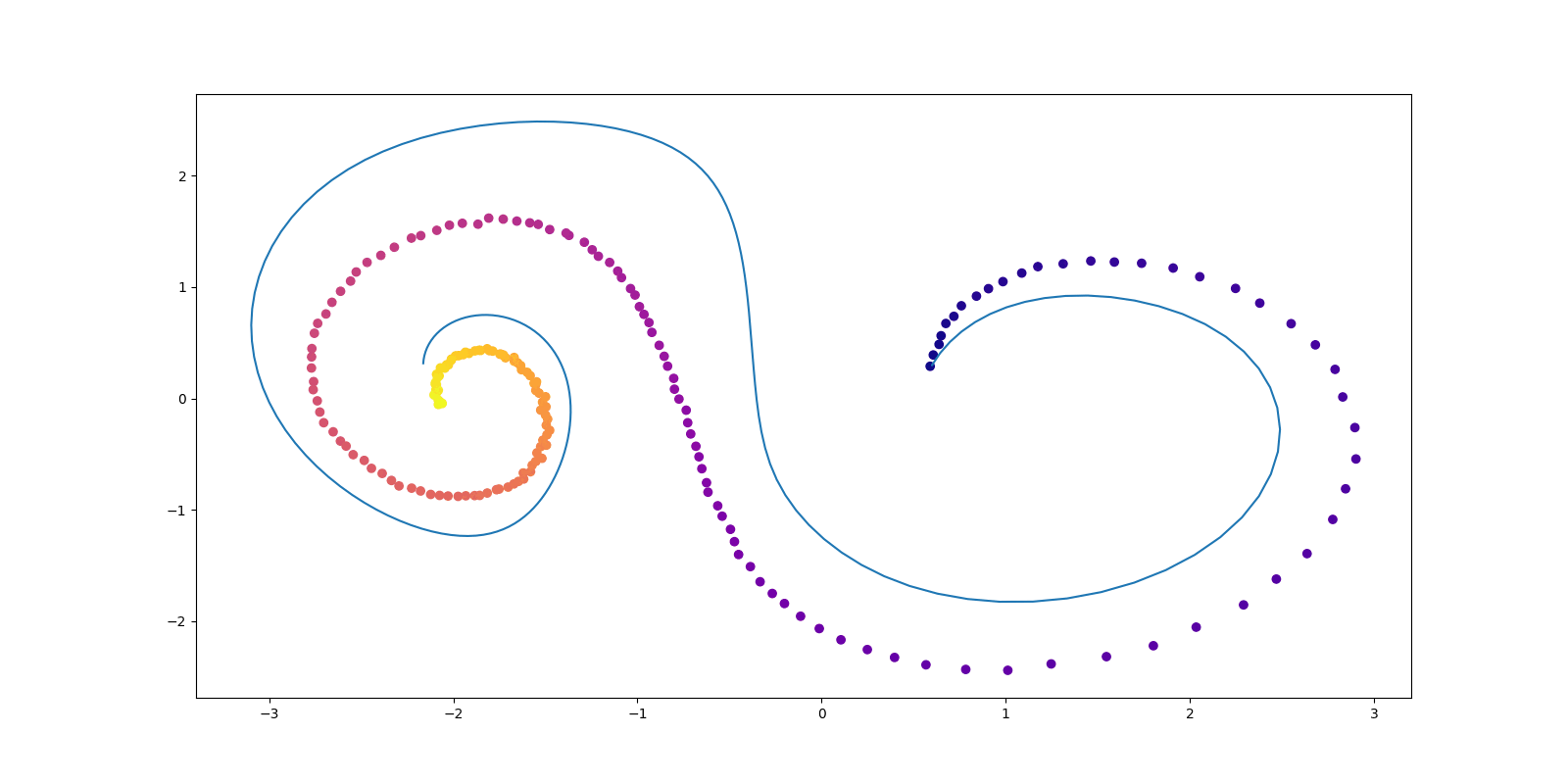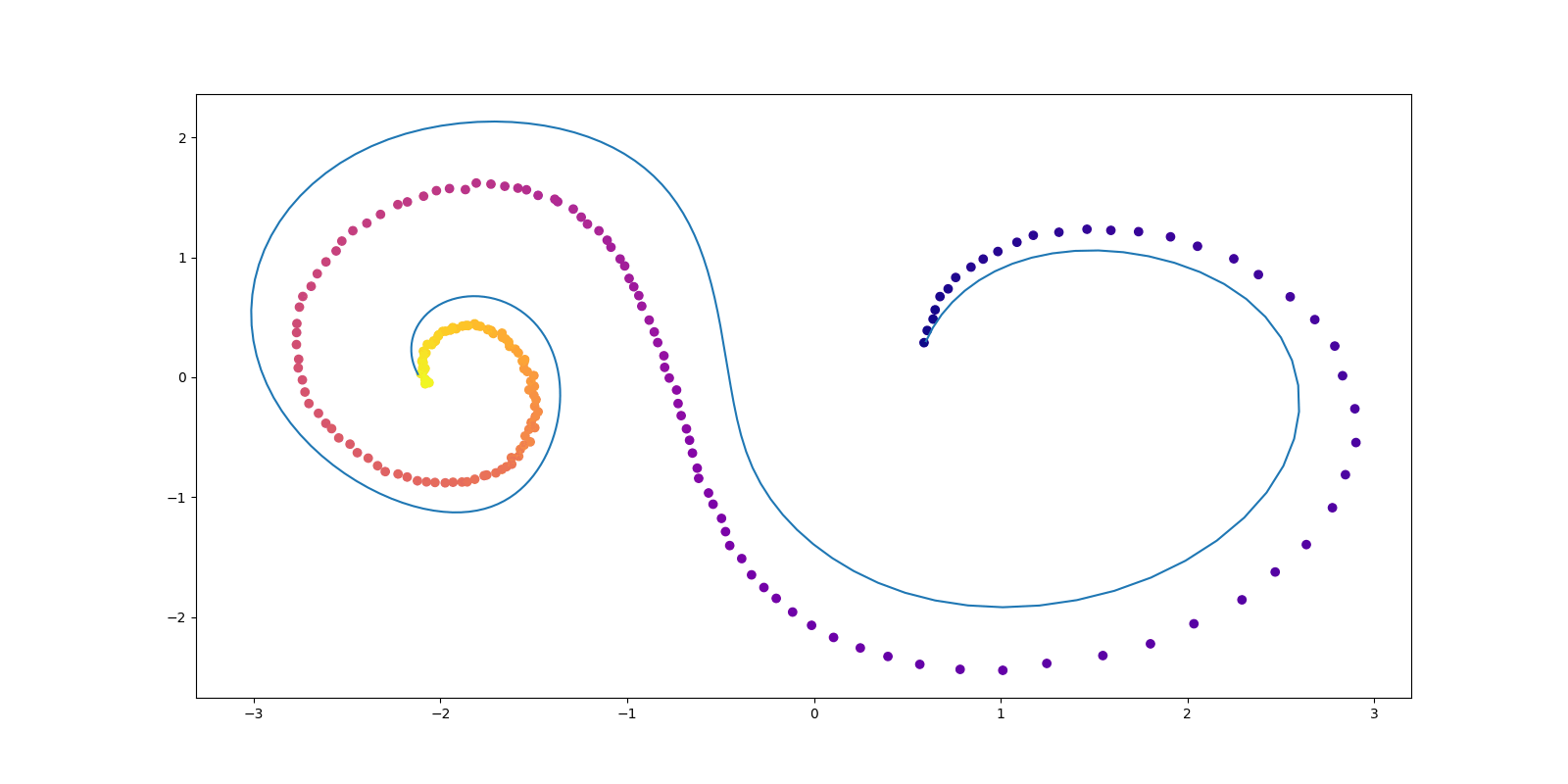
Mikhail Surtsukov 氏によるチュートリアルが，このレポジトリで公開されている．

FFJORD (Grathwohl et al., 2019) の実装は，このレポジトリで公開されている．

References

Grathwohl, W., Chen, R. T. Q., Bettencourt, J., and Duvenaud, D. (2019). Scalable Reversible Generative Models with Free-form Continuous Dynamics. In International conference on learning representations.