分布道の学習としての生成モデリング
Denoising Diffusion から Schrödinger Bridge へ
2024-08-03
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
関連ページ
1 導入
1.1 サンプラーに使う
一方で本稿では，正規化定数が不明な分布 \[ \pi(x)=\frac{\gamma(x)}{Z},\qquad Z:=\int_\mathcal{X}\gamma(x)\,dx \] に対しても使える汎用サンプラー DDS (Denoising Diffusion Sampler) (Vargas et al., 2023) とその Schrödinger 橋による改良を扱う：
1.2 DDS の現状
MCMC, SMC そして ABC の代替手法ともくされているが，理論が未発達である．例えば (Bortoli, 2022) などの既存の理論は，スコア関数の推定誤差の言葉で収束を論じており，この推定誤差は実践上では確認が難しいものであると言える (Heng et al., 2024)．
加えて，拡散模型は確率的局所化の考え方と関係が深いことが知られており，近似メッセージ伝搬を取り入れることで，定量的な収束保証をつけることもできる (Montanari and Wu, 2023)．
1.3 AIS (Neal, 2001) との比較
焼きなまし重点サンプリング (AIS: Annealed Importance Sampling) では，目標分布 \(\pi\) に至る列 \(\pi_0,\cdots,\pi_p=\pi\) が得られており，\(\pi_0\) からのサンプリングは可能である場合の重点サンプリング法のテクニックである．
具体的には，拡張された空間 \(\mathcal{X}^{p+1}\) 上の目標分布 \[ \pi_p\otimes P_p'\otimes\cdots\otimes P_1' \] に対して \(\pi_0\otimes P_1\otimes P_2\otimes\cdots\otimes P_p\) を提案分布に用いたとして荷重荷重を計算する．特に (Neal, 2001) では \(P_i'\) として \[ P_i(x_{i-1},x_i)\pi_{i-1}(x_i-1)=\pi_i(x_i)P_i^{-1}(x_{i-1},x_i) \] を満たす後ろ向き核 \(P_i^{-1}\) を用いており，この場合の重点荷重は次の表示を持つ：1 \[ w(X_{1:p}):=\frac{\pi_p(X_p)}{\pi_{p-1}(X_{p})}\frac{\pi_{p-1}(X_{p-1})}{\pi_{p-2}(X_{p-1})}\cdots\frac{\pi_2(X_2)}{\pi_1(X_2)}\frac{\pi_1(X_1)}{\pi_0(X_1)} \]
すなわち，AIS では \(\mathcal{X}^{p+1}\) 上で重点サンプリングを行い，\(x_p\) の成分のみに注目することで周辺分布では \(\pi_p\) に対する効率的な重点サンプリングが実現される，という手法であるが，その分効率が落ちている (Doucet et al., 2022)．
例えば目標分布 \(\pi_p\) からのシミュレーションが実は可能で，\(P_i\equiv\pi_p\) と取れる場合，重点サンプリングは正確に行えるが，AIP は迂回した分 \[ \mathrm{V}[\log w(X_{1:p})]=\sum_{i=1}^p\mathrm{V}\left[\log\frac{\pi_i(X_i)}{\pi_{i-1}(X_i)}\right]>0 \] という分散が発生してしまう．
または，ある \(\pi_p\) に収束する MCMC 核 \(P\) に関して \(P_i\equiv P\) と取った場合，もし比 \[ \frac{\pi_p(X_p)}{\pi_0P_1\cdots P_p(X_0)} \] が計算できたならば，十分 \(p>0\) を大きく取ることで極めて効率的な重点サンプリングが可能になるが，AIS では \(w\) の分散が大きくなってしまう．
実は，分散を最小にする \(\mathcal{X}^{p+1}\) 上での提案分布は，後ろ向き確率核 \(P_i^{-1}\) ではなく，提案分布 \(Q:=\pi_0\otimes P_1\otimes P_2\otimes\cdots\otimes P_p\) の時間反転が与える (Del Moral et al., 2006)．
1.4 非一様 Langevin 過程を用いるもの
連続な架橋 \((\pi_t)_{t\in[0,p]}\) を取り， \[ dX_t=\nabla\log\pi_t(X_t)\,dt+\sqrt{2}\,dB_t,\qquad X_0\sim\pi_0, \] を連続時間極限とするような離散化 \[ P_k(x_{k-1},dx_k):=\mathrm{N}_d\biggr(x_{k-1}+\delta\nabla\log\pi_k(x_{k-1}),2\delta I_d\biggl),\qquad\delta>0, \] を考える．これは (Heng et al., 2020), (Wu et al., 2020), (Thin et al., 2021) などで扱われている．この過程が時刻 \(p\) において \(\mathrm{N}_d(0,I_d)\) とどれほど乖離があるかの知見は，模擬アニーリングに対する数理解析の下で蓄積されている (Fournier and Tardif, 2021), (Tang et al., 2024)．
この時間反転は (Haussmann and Pardoux, 1986) により導かれている： \[ d\overline{X}_t=\biggr(-\nabla\pi_{T-t}(\overline{X}_t)+2\nabla\log q_{T-t}(\overline{X}_t)\biggl)\,dt+\sqrt{2}d\overline{B}_t,\qquad\overline{X}_0\sim q_T, \] ただし，\(q_t\) は \((X_t)\) の周辺分布とした．
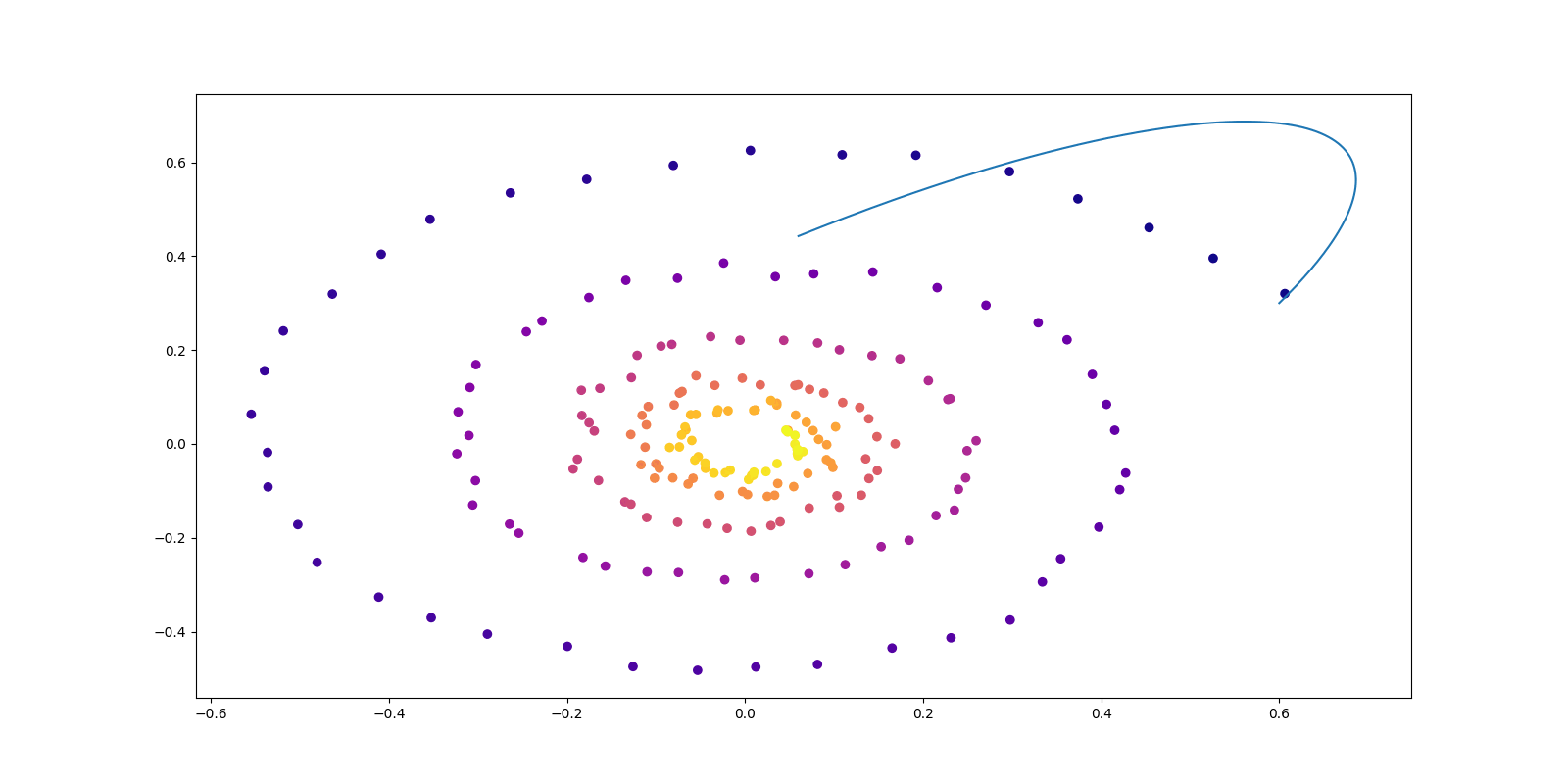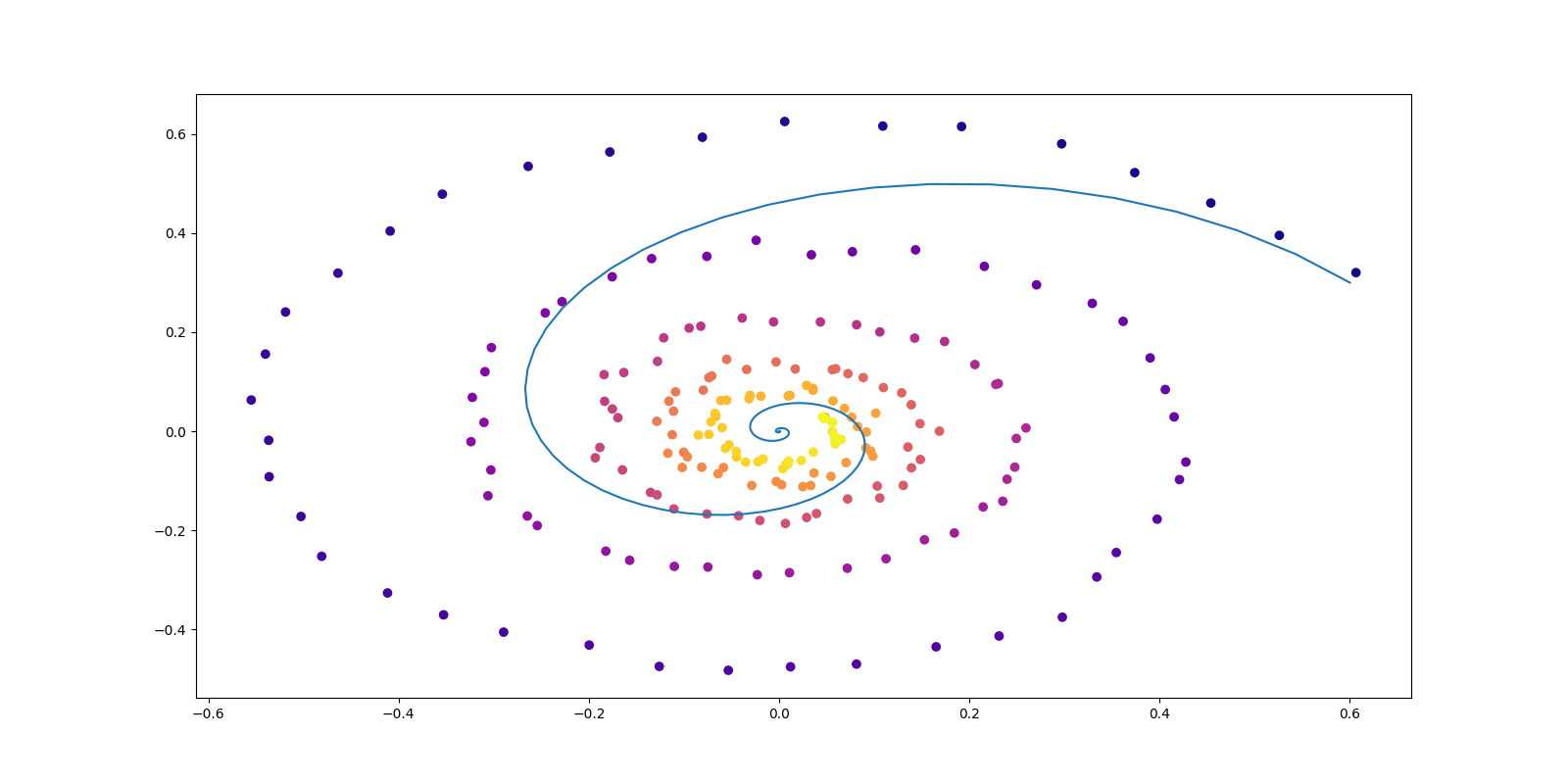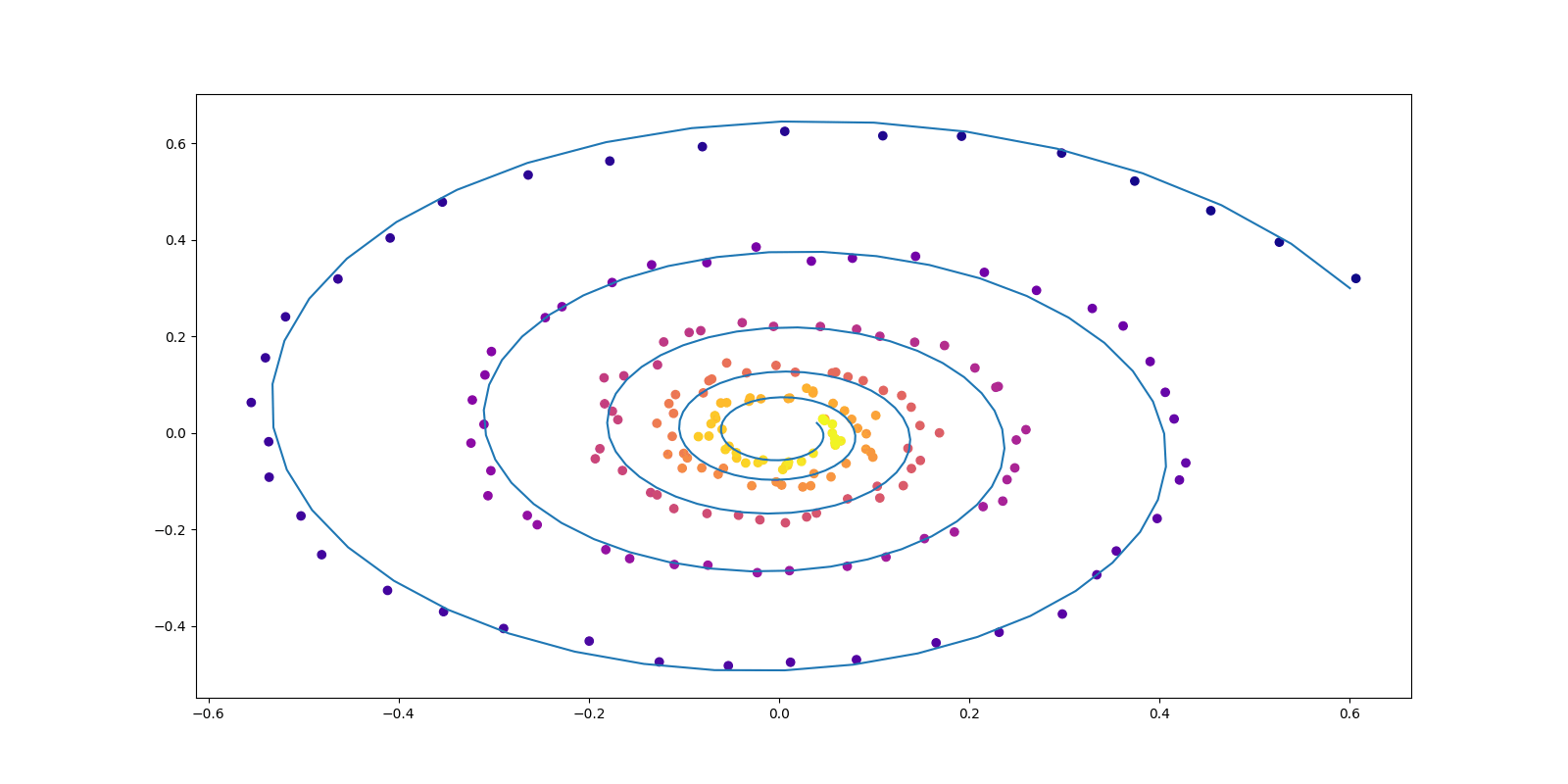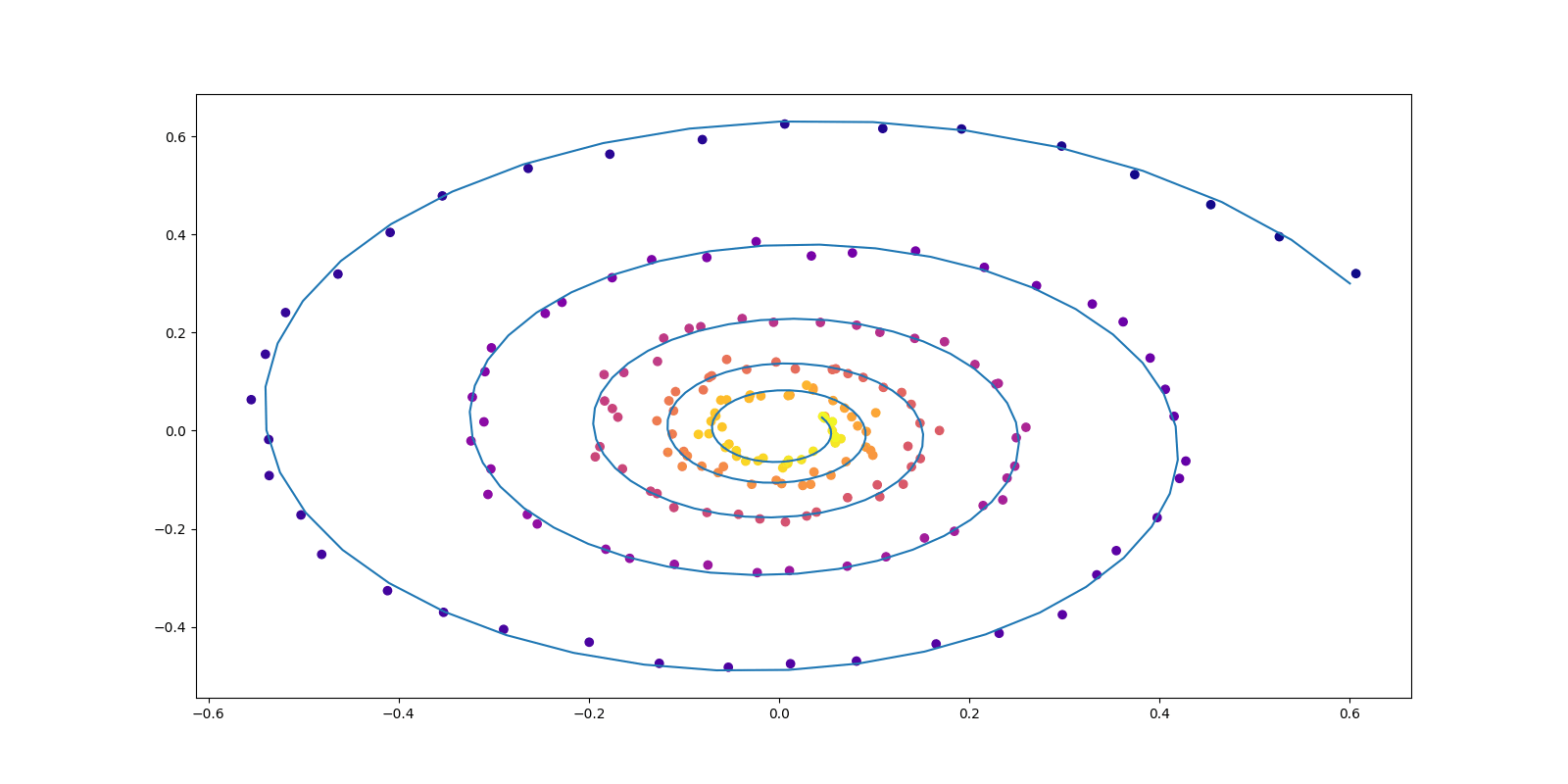
2 雑音除去拡散によるサンプリング (DDGS)
2.1 はじめに
(Vargas et al., 2023) は次の２点を克服するサンプラーを提案した．
2.1.1 条件付き生成
DDPS と DSB-PS は，\(y\in\mathcal{Y}\) について一様に均してしまった 償却推論 を行っている．
特殊な \(y\in\mathcal{Y}\) に対しても，これにフィットしたモデルを作りたい状況がある．
2.1.2 正規化定数のわからない分布
同時に DDPS と DSB-PS は，正規化定数の不明な分布などからのサンプリングには使えない．
ここでは， \[ p(x)=\frac{\gamma(x)}{Z},\qquad Z:=\int_\mathcal{X}\gamma(x)\,dx \] という形で，\(\gamma\) のみを与えられた場合を考える．
DDPS において考えたように，\((X_0,Y)\) からのサンプルが得られないため，\(\nabla_x\log p_t(x_t)\) の項の近似に関しては別のアプローチを考える必要がある．
2.2 \(h\)-変換としての表示
雑音除去拡散 \[ dZ_t=\frac{1}{2}Z_t\,dt+\nabla_z\log p_{T-t}(Z_t|y)\,dt+dW_t,\qquad Z_0\sim p_T(x_T|y), \] の \(\nabla_x\log p_t(x_t)\) の表示が消えるような変数変換を考える．
まず，OU 過程 \((X_t)\) を定常分布 \(X_0\sim\mathrm{N}_d(0,I_d)\) から始めた場合の分布を \(\mathbb{M}\) とすると，この逆は \[ dZ_t=-\frac{1}{2}Z_t\,dt+dW_t,\qquad Z_0\sim\mathrm{N}_d(0,I_d), \] である．この過程の \(\mathbb{M}\) の下での \(h\)-変換は， \[ dZ_t=-\frac{1}{2}Z_t\,dt+\nabla_z\log h_{T-t}(Z_t)\,dt+dW_t,\qquad Z_0\sim p_T(x_T), \] \[ h_t(x_t):=\int_\mathcal{X}\Phi(x_0)m_{T|T-t}(x_0|x_t)\,dx_0,\qquad \Phi(x_0):=\frac{p(x_0)}{\phi_d(x_0;0,I_d)} \] と表せる．ただし \(m\) は OU 過程 \((X_t)\) の遷移密度とした．
この表示に対するパラメトリックな近似 \[ dZ_t=-\frac{1}{2}Z_t\,dt+u^\theta_{T-t}(Z_t)\,dt+dW_t,\qquad Z_0\sim\mathrm{N}_d(0,I_d), \] の分布を \(\mathbb{Q}^\theta\) で表し，\(\operatorname{KL}(\mathbb{P},\mathbb{Q}^\theta)\) を最小化することが最初に思いつくが，これでは \(\mathbb{P}\) からのサンプル，従って \(p\) からのサンプルを必要としてしまう．
2.3 逆 KL-乖離度の最適制御
\(h\)-変換をした理由は，\(\operatorname{KL}(\mathbb{Q}^\theta,\mathbb{P})\) ならば計算できる点にある．
\[ \mathcal{L}(\theta):=\operatorname{KL}(\mathbb{Q}^\theta,\mathbb{P})=\operatorname{E}_{\mathbb{Q}^\theta}\left[\frac{1}{2}\int^T_0\|u^\theta_{T-t}(Z_t)\|^2\,dt-\log\Phi(Z_T)\right] \] については，\(\log\Phi(Z_T)\) には \(\theta\) が出現しないため，第一項のみに集中すれば良い．
そうすると，これは KL 最適制御問題として解くことができる．
3 Schrödinger 橋によるサンプリング (DSB-GS)
3.1 はじめに
全く同様にして，Schrödinger 橋としての見方を導入することにより，DDGS の効率はさらに上げられる．
加えて，無雑音極限において，Schrödinger 橋問題は，エントロピー正則化を持つ最適輸送問題と Monge-Kantorovich 問題と関連がある (De Bortoli et al., 2021, p. 3.1節)．
この場合も，\(T\to\infty\) の極限において，DDGS は Schrödinger 橋の近似を与える．
3.2 Schrödiger-Föllmer サンプラー
\(\mathbb{M}\) を OU 過程と取る代わりに，\(\Pi_T(x_T)\) を Dirac 測度として Brown 橋を取ることもできる．これが (Föllmer, 1985) 以来のアプローチである．
このアプローチでは，IPF は２回のイテレーションで収束するという美点がある．このための数値的方法も広い分野で提案されている：(Barr et al., 2020), (Zhang et al., 2021)．
終端の測度を Dirac 測度としていることの綻びが数値的な不安定性に現れやすいことが (Vargas et al., 2023) で述べられている．
References
Barr, A., Gispen, W., and Lamacraft, A. (2020). Quantum ground states from reinforcement learning. In J. Lu and R. Ward, editors, Proceedings of the first mathematical and scientific machine learning conference,Vol. 107, pages 635–653. PMLR.
Bortoli, V. D. (2022). Convergence of denoising diffusion models under the manifold hypothesis. Transactions on Machine Learning Research.
De Bortoli, V., Thornton, J., Heng, J., and Doucet, A. (2021). Diffusion schrödinger bridge with applications to score-based generative modeling. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems,Vol. 34, pages 17695–17709. Curran Associates, Inc.
Del Moral, P., Doucet, A., and Jasra, A. (2006). Sequential Monte Carlo Samplers. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(3), 411–436.
Doucet, A., Grathwohl, W. S., Matthews, A. G. D. G., and Strathmann, H. (2022). Score-based diffusion meets annealed importance sampling. In A. H. Oh, A. Agarwal, D. Belgrave, and K. Cho, editors, Advances in neural information processing systems.
Föllmer, H. (1985). An entropy approach to the time reversal of diffusion processes. In M. Metivier and E. Pardoux, editors, Stochastic differential systems filtering and control, pages 156–163. Berlin, Heidelberg: Springer Berlin Heidelberg.
Fournier, N., and Tardif, C. (2021). On the simulated annealing in rd. Journal of Functional Analysis, 281(5), 109086.
Haussmann, U. G., and Pardoux, E. (1986). Time Reversal of Diffusions. The Annals of Probability, 14(4), 1188–1205.
Heng, J., Bishop, A. N., Deligiannidis, G., and Doucet, A. (2020). Controlled sequential monte carlo. The Annals of Statistics, 48(5), 2904–2929.
Heng, J., Bortoli, V. D., and Doucet, A. (2024). Diffusion Schrödinger Bridges for Bayesian Computation. Statistical Science, 39(1), 90–99.
Montanari, A., and Wu, Y. (2023). Posterior sampling from the spiked models via diffusion processes.
Neal, R. M. (2001). Annealed Importance Sampling. Statistics and Computing, 11, 125–139.
Tang, W., Wu, Y., and Zhou, X. (2024). Discrete-Time Simulated Annealing: A Convergence Analysis via the Eyring-Kramers Law. Numerical Algebra, Control and Optimization.
Thin, A., Kotelevskii, N., Doucet, A., Durmus, A., Moulines, E., and Panov, M. (2021). Monte carlo variational auto-encoders. In M. Meila and T. Zhang, editors, Proceedings of the 38th international conference on machine learning,Vol. 139, pages 10247–10257. PMLR.
Vargas, F., Grathwohl, W. S., and Doucet, A. (2023). Denoising Diffusion Samplers. In The eleventh international conference on learning representations.
Wu, H., Köhler, J., and Noe, F. (2020). Stochastic Normalizing Flows. In H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, and H. Lin, editors, Advances in neural information processing systems,Vol. 33, pages 5933–5944. Curran Associates, Inc.
Zhang, B., Sahai, T., and Marzouk, Y. (2021). Sampling via controlled stochastic dynamical systems. In I (still) can’t believe it’s not better! NeurIPS 2021 workshop.