ベイズ統計学とスピングラス

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

ベイズ統計学と統計物理学

スパース符号の復元を題材として

上掲稿で扱ったスパース符号の復元の問題をさらに押し進め，より実用的な誤り訂正符号の設定を考える．

モデルにハイパーパラメータが増え，厳密に証明できる事項は大きく減る．（逆）温度パラメータ \(\beta>0\) が特定の値を取る際，厳密解が計算可能であり，これを 西森温度 と呼ぶ．¹ これは，ハイパーパラメータ \(\beta>0\) が指定する分布族が，真の事後分布を含む条件と等価になる．

1 誤り訂正符号

1.1 線型符号

有限体 \(\mathbb{F}_p\) 上の固定符号長 \(n\) を持つ 線型符号 とは，\(\mathbb{Z}\)-部分加群 \(C\subset\mathbb{F}_p^n\) のことである： \[ a(x+y)=ax+ay\quad(a\in\mathbb{Z},x,y\in C). \]

このクラスの符号については，Hamming 距離 \(d\) の最小値 \[ \min_{\substack{x,y\in C\\ x\ne y}}d(x,y) \] が線型時間で計算可能であるために，誤り訂正符号の例として重宝される．

例（最も単純な線型パリティ検査符号）²

\[ C:=\left\{\mathtt{000},\mathtt{011},\mathtt{101},\mathtt{110}\right\} \] とすると，\(\mathbb{F}_2^3\) 上の \(\mathbb{Z}\)-部分加群となっている．

加えて，この線型符号は次の構造を持つ：任意の符号語 \(x_1x_2x_3\in C\) について， \[ x_1+x_2\equiv x_3\mod 2. \] すなわち，真の符号は前半２ビット（情報ビット）に含まれており，最後の符号は パリティ検査ビット と呼ばれる．

１ビットの誤りまでなら，\(x_3\) の偶奇が変わるために，誤りを検出できる．このことを，\(C\) は単一パリティ検査符号であるという．

1.2 パリティ検査

定義（パリティ検査方程式）

\(n>k\in\mathbb{N}\) に対して，\((n,k)\)-線型符号 とは，ある行列 \(H\in M_{n,n-k}(\mathbb{F}_2)\) を用いて \[ C=\mathrm{Ker}\;H \] と定義される符号 \(C\subset\mathbb{F}_2^n\) のことをいう．このとき，\(H\) を パリティ検査行列，符号語 \(x\in C\) が満たす性質 \[ Hx=0 \] を パリティ検査方程式 という．

例（組織符号）³

前掲の例（第 1.1 節）のように，情報ビットと組織ビットが完全に分離している符号を 組織符号 という．

これは，ある行列 \(G\in M_{k,n-k}(\mathbb{F}_2)\) が存在して，白文 \(u\in\mathbb{F}_2^k\) に対する符号が \[ x=(I_k\;G)^\top u \] と表せる場合に当たる．

このとき，パリティ検査行列 \(H\in M_{n,n-k}(\mathbb{F}_2)\) を \[ H:=(G\;I_{n-k}) \] で定めると，パリティ検査方程式が成り立つ．

実際， \[ Hx=(G\;I_{n-k})(I_k\;G)^\top u=Ou=0. \]

こうして定まる \(H\) はパリティ検査行列の標準形ともいう．

パリティ検査行列における誤り訂正では，次の逆問題を考えることになる．

シンドローム復号

対称通信路が加法的ノイズを印加するならば，受信符号 \(y\) はあるベクトル \(e\in\mathbb{F}_2^n\) に対して \[ y=x+e \] の形で表される．

すると，パリティ検査方程式より， \[ s:=Hy=He \] が必要である．この値 \(s\) を シンドローム という．

シンドロームは誤りベクトル \(e\) のみの関数であるから，良い設定下では誤り \(e\) を推定することができる．

例（低密度パリティ検査）⁴

一般に，パリティ検査方程式 \[ s=He \] から \(e\) を推定する問題は計算量的に困難になる．

しかし，例えばパリティ検査行列が \[ H=(C_1\;C_2) \] \[ C_1\in M_{n-k,k}(\mathbb{F}_2),\quad C_2\in M_{n-k,n-k}(\mathbb{F}_2) \] と２つの疎行列の結合として表される場合（Gallager 符号 (Gallager, 1960) という），Bethe 近似による効率的な復号アルゴリズムが存在する．

1.3 スピングラスとの類似性

スピングラスとの類似性を最初に指摘したのは (Sourlas, 1989) であり，すぐに西森ラインとの関連性も知られた (Hidetoshi Nishimori, 2001)．

現在ではこの対応は誤り訂正符号に限らず，極めて広範な統計的推定問題に渡っていることが認識されている．

実際，スピングラス理論で開発されたレプリカ法，cavity method, 信念伝搬法は盛んに統計的推定問題に応用されている (Zdeborová and Krzakala, 2016)．

Perhaps the most important message we want to pass in this review is that many calculations that physics uses to understand the world can be translated into algorithms that machine learning uses to understand data. (Zdeborová and Krzakala, 2016, p. 457)

2 スピングラスと西森温度

スピングラス系にベイズ推定を紐づけることができる．

その際，伝統的にスピングラス理論で扱われた quenched ensemble とも annealed ensemble とも違う第三のアンサンブル planted ensemble を扱うことになる．

2.1 設定：２点相互作用のみを考えた Ising モデル

配置空間を \(x\in\{\pm1\}^N\) とし，\(N\) 個の頂点を持ったグラフ \(\mathcal{G}=(\mathcal{V},\mathcal{E})\) が定める Ising モデル \[ E(x,y)=-\sum_{(i,j)\in\mathcal{E}}y_{ij}x_ix_j \tag{1}\] を考える．

\(y_{ij}>0\) の場合 \(x_i,x_j\) は揃い，\(y_{ij}<0\) の場合 \(x_i,x_j\) は反対方向を向く方がエネルギー \(E\) が下がる．

フラストレーションについて

この系を絶対零度まで冷却した際，\((y_{ij})\) に指定された通りのルールを満たす配置 \(x\in\{\pm1\}^N\) があるならばその配置が出現するはずである．この場合，系はフラストレーションを持たないという．

そうでない場合でも，ファクターグラフ \((\mathcal{V},\mathcal{E},(y_{ij}))\) が定めるフラストレーションを最小にした基底状態が見つかるはずである．

なお，あるファクターグラフがフラストレーションを持たないかどうかは，クラス P に属する問題である．すなわち，多項式時間で判定可能である．⁵

相互作用項 \(y_{ij}\) が確率的に与えられる場合，その系を スピングラス という．

スピングラス理論で代表的な (Edwards and Anderson, 1975) モデルでは，\(\{y_{ij}\}\) はある簡単な分布の独立同分布確率変数だとして，系の振る舞いを分析する．⁶

一方でここでは，確率変数 \(y_{ij}\) は次に説明するように定まると考えることで，スピングラス系とベイズ推定問題との対応が明らかになる．⁷

2.2 スピングラス系のベイズからの解釈

統計的な手続きは，スピングラス系を特殊な方法で生成し，その基底状態を探る逆問題として理解できる．⁸ こうして生成されたスピングラスを planted ensemble と呼ぶ．

具体的には，前稿 で扱った信号推定の問題で，情報源の分布 \(p(x)\) と通信路の分布 \(p(y|x)\) が，あるパラメータ \(\alpha,\beta\) の分だけ一般化し，次の過程を考える：

planted ensemble⁹

1. 配置 \(x\in\{\pm1\}^N\) をある分布 \(p_\alpha(x)\) に従って選ぶ．¹⁰
2. 相互作用項 \(y\) を，この \(x\) と式 (1) で定まる Hamiltonian \(E\) が定める Boltzmann 分布 \(p_\beta(y|x)\) からサンプリングする： \[ p_\beta(y|x):=\frac{e^{-\beta E(x,y)}}{\mathcal{Z}_\beta} \] \[ \mathcal{Z}_\beta:=\sum_{y\in\mathcal{E}}e^{-\beta E(x,y)} \]
3. 観測者は \(y\) のみを見て，\(x\) がなんだったかを考える．\(y\) を生成するのに用いたパラメータの真値 \(\alpha^*,\beta^*\) も未知とする．¹¹

最初に設定される Ising スピンの配置 \(x\in\{\pm1\}^N\) を信号とみなすと，ノイズが加わった観測とは coupling \(y_{ij}\) のみを見ることに対応する．

そして信号推定とは，この \(y_{ij}\) が定める Hamiltonian \(E(x,y)\) の基底状態を探索することに他ならない．信号 \(x\) が，planted ensemble の基底状態に埋め込まれているわけである．

例（planted ensemble と同一視できる系）¹²

二元対称通信路における誤り訂正符号のスピングラス的解釈（第 1.3 節）はこの例の１つに過ぎない．

さらに，\(x\) を一般の潜在変数とし，事前分布 \(p(x)\) と確率核 \(p(y|x)\) が定める確率的グラフィカルモデルは，すべてこの枠組みに収まる．

以上，Bayes 推定の文脈でスピングラスの planted ensemble を定義したが，同様にしてスピングラス系の中に情報を隠すことは，よく見られるモデリング法である．

• Hopfield モデル (Hopfield, 1982) はランダムな配置を記憶させたスピングラス系であり，脳科学において連想記憶のモデルとしても用いられる．
• タンパク質の折りたたみ構造をモデリングするとき，その native configuration を基底状態として埋め込むことがある (Bryngelson and Wolynes, 1987)．
• グラフ内の大規模なクリークを見つける問題の難易度を，対応する planted ensemble における MCMC の収束の遅さとして捉えることができる (Mark Jerrum, 1992)．
• 同様に，グラフの２分割問題と擬似アニーリングとにも対応が存在する (M. Jerrum and Sorkin, 1993)．
• 充足性問題（四色問題など）の計算複雑性も，planted ensemble に対応させて示された (Achlioptas and Coja-Oghlan, 2008)．

The authors find that making the connection between planting and inference very explicitly brings a lot of insight into a generic inference problem and for this reason we built the present review around this connection. (Zdeborová and Krzakala, 2016, p. 469)

比例的高次元漸近論

\(M:=\lvert\mathcal{E}\rvert\) が観測 \(y\) のサイズとなる．

従来の統計学における漸近理論では，パラメータの次元 \(N\) は固定とし，\(M\to\infty\) の極限での理論が展開された．

現代では，モデルのサイズも大きくする \(N\to\infty\) の極限を考える需要が高まっている．

しかしこの場合でも，統計力学のツールボックスはこれを可能にする．

特に，比 \(\alpha:=\frac{M}{N}\) を保ったまま \(N,M\to\infty\) の極限を考えるスキームは 比例的高次元 と呼ばれる．

一般に，\(\alpha\) が十分大きい場合は，モデルの複雑性に対して観測も多いので，意味のある情報が引き出せるはずであり，\(\alpha\) が小さいほど困難になっていくはずである．

実際に，比例的高次元極限では，前稿でみた閾値現象が普遍的に生じることが知られている．これが，スピングラスの相転移に対応するのである．

2.3 西森ライン

前節 2.2 の解釈では，観測 \(y\) を経たあとの信号 \(x\) の事後分布は \[\begin{align*} p_{\alpha,\beta}(x|y)&\,\propto\,p_\beta(y|x)p_\alpha(x)\\ &=\frac{e^{-\beta E(x,y)}p_\alpha(x)}{\mathcal{Z}_{\alpha,\beta}} \end{align*}\] \[ \mathcal{Z}_{\alpha,\beta}:=\sum_{x\in\mathcal{E}}e^{-\beta E(x,y)}p_\alpha(x) \] で与えられる．

ただし，ここで，観測者の立てたモデルにおいて，パラメータ \(\alpha,\beta\) は真の値 \(\alpha^*,\beta^*\) とは異なり得るとする．

仮に観測者の用いたパラメータが真のパラメータと一致していた \((\alpha,\beta)=(\alpha^*,\beta^*)\) の場合，種々の魅力的な性質が成り立つ．これを西森条件という．¹³

中でも特に，次の性質は 西森対称性 と呼ばれている：¹⁴ \[ \operatorname{E}[f(X_1,X_2)]=\operatorname{E}[f(X^*,X_2)] \] ただし，\(X_1,X_2\) は事後分布からのランダムサンプル（平衡状態にあるレプリカ）であり，\(X^*\) は \(p(x)\) に従う真の信号とした．

この西森対称性を通じて，自由エネルギー（＝ KL 乖離度）をはじめとした厳密解が求まるのである．そのことを簡単なモデルで確認したのが 前稿 である．

西森対称性の含意

西森対称性とは，planted ensemble において，元々の配置 \(x^*\) は，Boltzmann 分布の平衡状態からのサンプル \(X\) と平均的に（マクロ的には）見分けがつかないという性質である．

西森対称性を用いた厳密解は，前稿で多く紹介している：

ベイズ統計学と統計物理学

スパース符号の復元を題材として

前稿では信号推定の問題を扱ったが，情報源分布 \(p(x)\) と通信路 \(p(y|x)\) のモデルがすでにわかっていることは，西森条件に相当する．

すなわち，信号推定の問題は，自然に西森ライン上で議論している場合に当たるのである．

一般に，事後平均推定量 \(\widehat{X}_n\) が平均自乗誤差を最低にするのであった：

\[ \operatorname{E}[(\widehat{X}_n-X^*)^2]=\min_{\widehat{X}_n}\operatorname{E}[(\widehat{X}_n-X^*)^2] \]

一般にこの値は不可知であるが，西森ライン上では＝モデルの特定が成功している場合，\(\widehat{X}_n\) の分散に平均的に（＝\(\operatorname{E}\) 内で）一致することになる．

これが 命題 \[ \DeclareMathOperator{\MMSE}{MMSE} \MMSE=\operatorname{E}[X^2]-\operatorname{E}\biggl[\langle X\rangle^2\biggr] \] の意味であるとも見れる．

換言すれば，Boltzmann 分布のうち，\(\beta\) が真値 \(\beta^*\) に一致する場合のみ，Bayes 推定の観点からは特別な意味を持つことになる．これを 西森温度 というのである．

2.4 Planted Ensemble の新規性

スピングラスでは，ランダムに定まる相互作用項 \(Y_{ij}\) と，これが定める Boltzmann 分布 \(\frac{e^{-\beta H}}{\mathcal{Z}}\) の２つの平均が存在する．

後者に関する平均は \(\langle X\rangle:=\operatorname{E}[X|Y]\) で表す一方で，前者に関する平均はよく \([-]\) で表される．¹⁵

従来のスピングラス理論では，disorder \(Y_{ij}\) に関する quenched average \([-]\) を先に取ることで，従来の Ising 模型と同様の議論に持ち込む戦略が取られる．

スピングラス理論における２つの平均¹⁶

系が大きくなるほど，\(\frac{\log Z_N}{N}\) の値はその quenched average に集中していく．¹⁷

従ってこの quenched average を求めることが中心問題とされる： \[ f=\lim_{N\to\infty}-\frac{1}{\beta N}[\log Z]. \] これは，自由エネルギー密度の quenched average と呼ばれる．

しかしこれに解決が難しく，値を計算するヒューリスティックとしてレプリカトリックが用いられる： \[ f\approx-\lim_{N\to\infty}\frac{1}{\beta N}\lim_{n\to\infty}\frac{[Z^n]-1}{n}. \]

一方で，次の値は計算が簡単であり，quenched average の下からの評価として用いられることがある： \[ f_{\text{annealed}}:=-\frac{1}{\beta N}\log[Z]. \] これは annealed average と呼ばれる．

こうして，quenched ensemble, average ensemble の両方が用いられることがあるが，この両方に共通していたのが \(Y_{ij}\) に関する平均を先に取る という点である．

しかし，planted ensemble ではこのアプローチをとっていない．

This notion of averaging over disorder is so well engraved into a physicist’s mind that going away from this framework and starting to use the related (replica and cavity) calculations for a single realization of the disorder has lead to a major paradigm shift and to the development of revolutionary algorithms such as the survey propagation (M. Mézard et al., 2002).

なお，この要約伝搬法は Bethe 近似に関係がある (Kabashima, 2005)．

一方で，planted ensemble では，スピンの配置を決めてから，\(Y_{ij}\) を生成している．当然，実際の物理過程とは違うものであり，Monte Carlo 法の真逆をやっているものであるが，ベイズ統計学との関連の結節点になる．

それだけでなく，スピングラス転移などの物理現象に関しても示唆を与える対象だとわかりつつある．¹⁸

2.5 レプリカ対称性の破れ

レプリカ対称性は大雑把に，平衡状態のダイナミクスの緩和過程によって表現できる．

事後分布 \(p(x|y)\) について

レプリカ法によるレプリカ対称性の破れパターン¹⁹

• レプリカ対称 であるとは，この平衡分布からスタートする MCMC が，系が大きくなる極限 \(N\to\infty\) で，どの平衡状態も一様に線型の複雑性でサンプリング可能であることをいう．²⁰
• d1RSB (dynamical one-step of replica symmetry breaking) とは，系が大きくなる極限 \(N\to\infty\) に対して線型の複雑性でサンプリング可能な平衡状態が，指数減少していくことを言う．
• 1RSB (static one-step RSB) とは，平衡分布からスタートする MCMC がサンプリング可能な平衡状態が，全体の一部に留まることをいう．また，任意の２つの平衡状態の間の距離は，\(N\to\infty\) の極限で殆ど確実に，２つの値のいずれかのみを取ることを言う．
• FRSB (full-step RSB) とは，任意の２つの平衡状態の間の距離が，ある絶対連続分布に従うことをいう．

RSB 下では，\(N\to\infty\) の極限で，Boltzmann 分布の自己平均化＝測度の集中が起こらない．

例（自発磁化密度）²¹

平衡状態から開始する Glauber 動力学を考えると，例えば \(d\ge2\) 次元での外場を持たない強磁性 Ising 模型では，臨界温度以下である限り， \[ \lim_{t\to\infty}\lim_{N\to\infty}\langle\sigma_i(t)\rangle_G\ne\langle\sigma_i\rangle \] が成り立つ．ただし，\(\langle-\rangle_G\) は特定の初期状態を持つ Glauber 動力学に関する平均とした．

特に，ある自発磁化密度 \(M(\beta)>0\) が存在して， \[ \lim_{t\to\infty}\lim_{N\to\infty}\langle\sigma_i(t)\rangle_G\in\{\pm M(\beta)\} \] である．

この「準平衡状態」と言える状態にとらわれる現象は普遍的であるが，この「準平衡状態」が，初期位置の関数として，時間にも空間にも不変性が存在しないときが，スピングラスである．

3 A Planted Spin Glass Model of Error Correcting Codes

誤り訂正符号を例に取り，censored block model (Abbe et al., 2014) とも呼ばれる具体的な planted ensemble を考える．²²

3.1 設定

planted spin glass of error correcting code

• \(p_\alpha(x)\) を \(\{\pm1\}^N\) 上の 一様分布とする．
• 辺の集合 \(\mathcal{E}\) は，大きさ \(M\) で，ランダムに生成されるものとする．²³
• \(p_\rho(y|x)\) は，ある確率 \(\rho\in(0,1)\) に関して， \[ p(y_{ij}|x_i^*,x_j^*)=\rho\delta_{y_{ij},x_i^*x_j^*}+(1-\rho)\delta_{y_{ij},-x_i^*x_j^*} \] の直積として定まるとする．²⁴

この設定下では，事後分布は \[\begin{align*} p(x|y)&=\frac{p(y|x)p(x)}{p(y)}\\ &=\frac{\prod_{(i,j)\in E}e^{\beta^*y_{ij}x_ix_j}}{2^N(2\cosh\beta^*)^Mp(y)} \end{align*}\] と表せる．ただし， \[ \beta^*:=\beta^*(\rho):=\frac{1}{2}\log\frac{\rho}{1-\rho} \tag{2}\] とした．

これは，Hamiltonian \[ H(x,y):=-\sum_{(i,j)\in\mathcal{E}}y_{ij}x_ix_j \tag{3}\] が定める Boltzmann 分布に他ならない．

証明²⁵

この設定下では， \[ \rho=\frac{e^{\beta^*}}{2\cosh\beta^*},\qquad\beta^*:=\frac{1}{2}\log\frac{\rho}{1-\rho} \] が成り立ち， \[ p(y_{ij}|x_i^*,x_j^*)=\frac{e^{\beta^*y_{ij}x^*_ix^*_j}}{2\cosh\beta^*} \] と表せるためである．

解釈

• まず，二元対称通信路における誤り訂正符号としての見方ができる (Iba, 1999, pp. 3879 3節)

  \((i,j)\in\mathcal{E}\) に関して， \[ y_{ij}^{\text{in}}:=x_ix_j \] が送信符号であるとし，確率 \(1-\rho\) で誤りが生じるとする： \[ y_{ij}=\begin{cases} y_{ij}^{\text{in}} & \text{with probability }\rho,\\ -y_{ij}^{\text{in}} & \text{with probability }1-\rho. \end{cases} \]

• 次に，teacher-student sinario としての見方もできる (Zdeborová and Krzakala, 2016, pp. 473–2.1節)

  \(N\) 人が，\(\pm1\) のいずれかが書かれたカードを持っているとし，教師はこれを知っているとする．

  生徒は，人物 \(x_i,x_j\) が持っているカードが一致しているならば \(y_{ij}=1\)，そうでないならば \(y_{ij}=-\) と知らされるが，正しく知らされる確率は \(\rho\) であるとする．

3.2 ベイズ推定からの解釈

そこで，前節の計算に基づき，事後分布を分布族 \[ p(x|y)\,\propto\,e^{-\beta H(x,y)},\qquad\beta>0, \tag{4}\] によりモデリングしたとすると，\(\beta=\beta^*(\beta)\) の場合が真の事後分布に当たる．

ただし，この真のハイパーパラメータの値 \(\beta^*(\rho)\) はわからないとする．

このとき例えば，平均正解個数を最大化した MMO (Maximum Mean Overlap) 復号をしたいならば，²⁶ \[ \widehat{x}_i=\mathrm{sign}(\langle x_i\rangle) \tag{5}\] というように，planted spin glass 系の平衡状態における磁化密度を計算することで達成できる．汎用的には，Monte Carlo 法を通じて解けることになる．²⁷

こうして，推定の問題が，スピングラスの planted ensemble の平衡状態のシミュレーションや基底状態の探索の問題に翻訳されたことになる．

特に，\(\beta=\beta^*(\rho)\) に設定した場合のみ，西森条件が成り立ち，これを満たす値 \((\beta,\rho)\) の集合を西森ラインという．

3.3 西森ラインの発見

西森ラインは元々，純粋に Hamiltonian \(H\) と Boltzmann 分布 (4) を持つ Edwards-Anderson モデルの解析の中で発見されたものであり，ベイズ統計学との関連はその約 10 年後になってから見出された．

3.3.1 ゲージ変換

(H. Nishimori, 1980) では，この Hamiltonian (3) が，任意の点 \(\widetilde{x}\in\{\pm1\}^N\) が定める次の変換に対して不変であることが利用された： \[ x_i\mapsto x_i\widetilde{x}_i, \] \[ y_{ij}\mapsto y_{ij}\widetilde{x}_i\widetilde{x}_j. \]

この変換を真の配置 \(\widetilde{x}=x^*\in\{\pm1\}^N\) について考える．真の配置 \(x^*\) がこのゲージ変換を受けると，全てのスピンが \(1\) に揃った状態に写される．

続いて，相互作用項 \(y_{ij}\) は，確率 \(\rho\) で \(y_{ij}=1\)，確率 \(1-\rho\) で \(y_{ij}=-1\) を満たす独立同分布列となる．

こうして，今回の設定 3.1 も Edwards-Anderson モデルに帰着され，この設定の中で全てのスピンが揃った強磁性状態を探索する問題に変換される．

この \(\{y_{ij}\}\) に関する Edwards-Anderson モデル \(H\) において，\(\rho\) と \(\beta\) の値の関係が系の振る舞いを決定し，その相図は元々の planted ensemble の性質と同一視できる．²⁸

3.3.2 西森ライン上での西森条件

このとき，Edwards-Anderson モデルは \(\beta=\beta^*\) （式 2）の場合に限り，内部エネルギーや比熱の上限が厳密解を持つ：²⁹ \[ \langle E\rangle=-M\tanh\beta^*. \tag{6}\]

この条件 \(\beta=\beta^*(\rho)\) を満たす組 \((\beta,\rho)\) を，\(T\)-\(p\) 相図上で見たとして，西森ライン と呼んだのであった．³⁰

平均次数 \(3\) を持つランダムグラフ上の \(\pm1\) Edwards-Anderson モデルの \(T\)-\(p\) 相図．(Zdeborová and Krzakala, 2016, p. 477 Figure. 2) から．

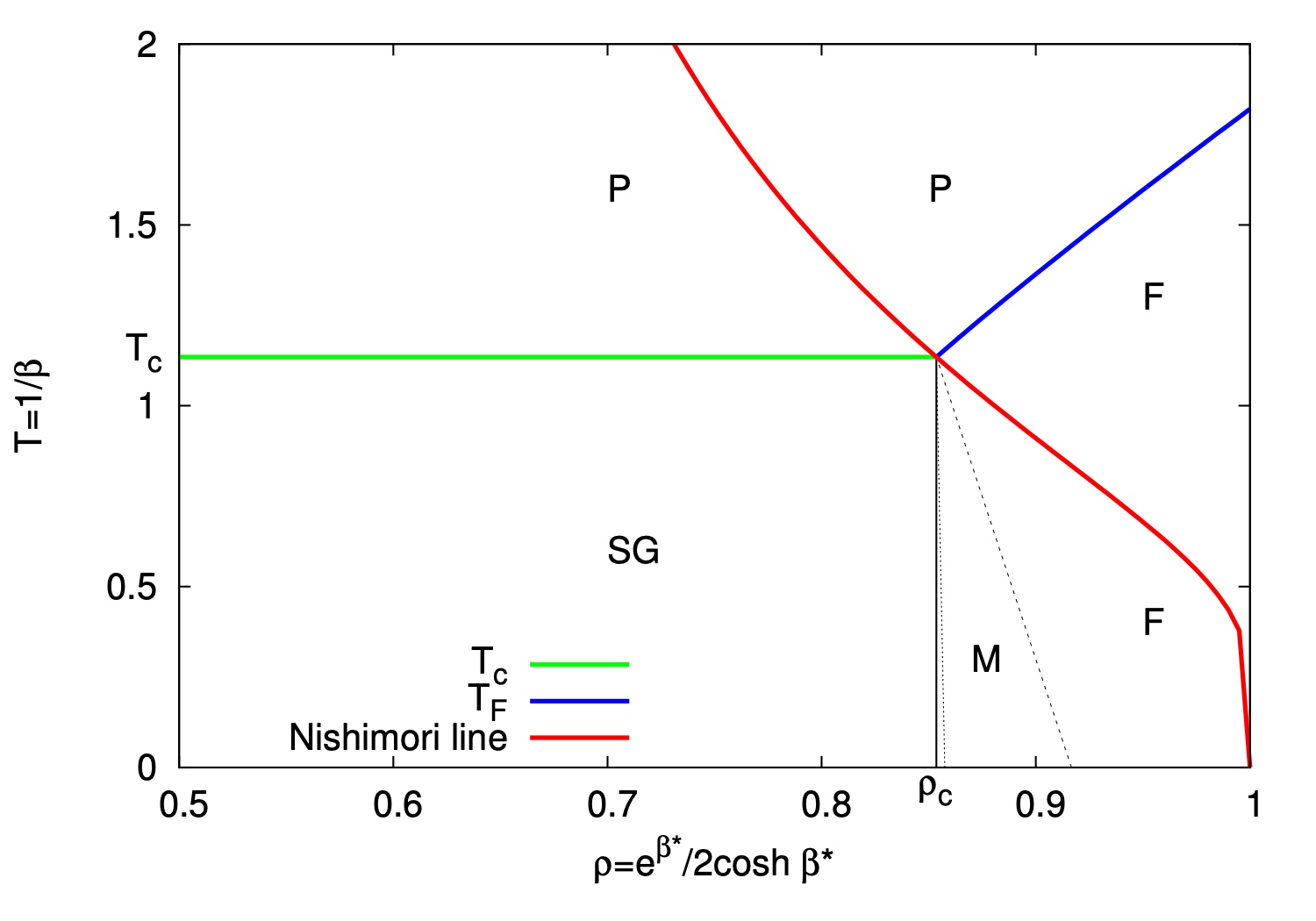
西森ラインは，相転移点 \(\beta_c\) を通るにも拘らず，内部エネルギーは常に特異性を示さない．特異部が消えているのである．³¹

そして何より，途中でスピングラス相を通過しない．³²

3.4 西森ラインの意味

一般の模型に対してこのようなゲージ変換が見つかるわけでもなければ，その変換の物理的な意味が定かでない．

3.4.1 ベイズによる解釈と一般化

しかし，西森ラインとは，今回の設定 3.1，または一般の planted spin glass model （第 2.2 節）において，モデルが正しく特定されていること \(\beta=\beta^*\) の特別な場合と理解できる (Iba, 1999)．

西森ラインの存在は長らく謎であったが，ベイズ推論の文脈では明確な意味を持つのである．特に，ゲージ対称性が存在しないモデルであっても，第 2.2 節の teacher-student scenario に当てはまる統計問題である限り，対応するスピングラス系に西森ラインは考えられる．³³

西森条件とは，モデルが正しく特定されている場合に成り立つ魅力的な性質の数々であると理解できる．

3.4.2 西森ライン上でのベイズ推論

モデルの特定が正しかったとする：\(\beta=\beta^*\)．

高温領域 \(\beta^*<\beta_c,\rho<\rho_c\) では，\(\rho\) が \(1/2\) に近いことに対応する．対応する Edwards-Anderson モデルは常磁性相 P にある．もはやこの系は planted information \(x^*\) を憶えておらず，真値 \(x^*\) の推定が（情報理論的に）不可能である．

一方で，低温領域 \(\beta^*>\beta_c,\rho>\rho_c\) では，Monte Carlo 法は高速に強磁性状態へ収束する．Monte Carlo 法により熱平均 (5) を計算することで，真値 \(x^*\) を最適に推定できる．

これら２つの領域の中間に「推定可能だが，計算が困難」という状態（スピングラス相）は存在せず，２つの領域の間には二次の相転移が見られる．³⁴

\(T_c\) の値は，ランダムグラフ \(\mathcal{G}\) の平均次数が大きいほど大きくなる．即ち，観測の数が多いほど，真値 \(x^*\) を推定することが可能な範囲が広がる．

3.5 誤特定の場合にはスピングラス相が現れる

モデルの真のハイパーパラメータ \(\beta^*\) を知らなかった場合を考える．

\(\rho<\rho_c\) であるとき，推定は不可能である．系を低温にしていくとスピングラス相が現れ，Monte Carlo 法の収束は圧倒的に遅くなる．加えて，推定は不可能であるはずなのに，\(\beta\to\infty\) の極限でも磁化が残る．これは過適応・過学習の現象と対応する．

\(\rho>\rho_c\) であるとき，推定は可能であるが，系が低温過ぎると強磁性相が存在しない可能性があるどころか，スピングラス相が同居する相が出現する可能性さえある．従って，ハイパーパラメータ \(\beta\) を大きくしすぎないことが大事である．

スピングラス相，過学習，いずれの現象も，西森ライン上では見られない．スピングラス系の不可知な性質は，真のモデルが不明な場合の推定問題の困難さと同根なのである．

3.6 系の温度はハイパーパラメータに対応する

以上の，Edwards-Anderson 模型の相図は，統計推測において「ハイパーパラメータ \(\beta^*\) の選択が大事」であることを示唆してくれる．

実際，EM アルゴリズム (Dempster et al., 1977) はこれを考慮した MAP 推定と捉えられる．

変分推論２

EM アルゴリズム

EM アルゴリズムは，エビデンス \(p_\beta(x|y)\) を最大化するように \(\beta\) を調整することでハイパーパラメータの真値 \(\beta^*\) と MAP 推定量 \(x^*\) を同時に探索する．

具体的には，温度 \(\beta\) における自由エネルギーを計算し（\(E\)-ステップ），その最大化を図る（\(M\)-ステップ）ことを繰り返す．

スピングラスで西森ラインから外れた状態では物理量の正確な計算が困難であるように，EM アルゴリズムでも一般に \(E\)-ステップは intractable であることが知られている．

また，自由エネルギーの代わりに内部エネルギーを用い，最大値点 \(\beta^*\) で満たすべき条件である西森条件 (6) を用いて \(M\)-ステップを実行することも考えられる．³⁵

即ち，西森条件を「成り立ってほしい条件」として，ハイパーパラメータの最大化に用いる方法が EM アルゴリズムであるとも捉えられるのである．

4 終わりに

モデルの誤特定 \(\beta\ne\beta^*\) が起こった場合，統計解析は泥沼に陥る．

この「泥沼」とは，物理的に正確な意味で，スピングラスであったわけだ．

逆に，モデルを正しく特定できているとき．通信の問題において，encoding と channel のモデルが正しく理解されているとき，復号難易度は大きく下がるはずである．これが，西森ライン上で物理量の計算が一気に簡単になる理由である．

References

Abbe, E., Bandeira, A. S., Bracher, A., and Singer, A. (2014). Decoding binary node labels from censored edge measurements: Phase transition and efficient recovery. IEEE Transactions on Network Science and Engineering, 1(1), 10–22.

Achlioptas, D., and Coja-Oghlan, A. (2008). Algorithmic barriers from phase transitions. In 2008 49th annual IEEE symposium on foundations of computer science, pages 793–802.

Bryngelson, J. D., and Wolynes, P. G. (1987). Spin glasses and the statistical mechanics of protein folding. Proceedings of the National Academy of Sciences, 84(21), 7524–7528.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological), 39(1), 1–22.

Edwards, S. F., and Anderson, P. W. (1975). Theory of spin glasses. Journal of Physics F: Metal Physics, 5(5), 965.

Gallager, R. G. (1960). Low Density Parity Check Codes (PhD thesis). MIT. Retrieved from http://hdl.handle.net/1721.1/11804

Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Science, 79(8), 2554–2558.

Iba, Y. (1999). The Nishimori line and Bayesian statistics. Journal of Physics A: Mathematical and General, 32(21), 3875.

Jerrum, Mark. (1992). Large cliques elude the metropolis process. Random Structures & Algorithms, 3(4), 347–359.

Jerrum, M., and Sorkin, G. B. (1993). Simulated annealing for graph bisection. In Proceedings of 1993 IEEE 34th annual foundations of computer science, pages 94–103.

Kabashima, Y. (2005). Replicated bethe free energy: A variational principle behind survey propagation. Journal of the Physical Society of Japan, 74(8), 2133–2136.

Krzakala, F., Zdeborova, L., Angelini, M. C., and Caltagirone, F. (2015). Statistical physics of inference and bayesian estimation.

Mattis, D. C. (1976). Solvable spin systems with random interactions. Physics Letters A, 56(5), 421–422.

Mézard, Marc, and Montanari, A. (2009). Information, physics, and computation. Oxford University Press.

Mézard, M., Parisi, G., and Zecchina, R. (2002). Analytic and algorithmic solution of random satisfiability problems. Science, 297(5582), 812–815.

Nishimori, H. (1980). Exact results and critical properties of the ising model with competing interactions. Journal of Physics C: Solid State Physics, 13(21), 4071.

Nishimori, Hidetoshi. (2001). Statistical physics of spin glasses and information processing: An introduction. Oxford University Press.

Sourlas, N. (1989). Spin-glass models as error-correcting codes. Nature, 339(6227), 693–695.

Talagrand, M. (2011). Mean Field Models for Spin Glasses. Volume I: Basic Examples. Springer Berlin, Heidelberg.

Zdeborová, L., and Krzakala, F. (2016). Statistical physics of inference: Thresholds and algorithms. Advances in Physics, 65(5), 453–552.

横尾英俊. (2004). 情報理論の基礎. 共立出版.

樺島祥介, and 杉浦正康. (2008). コトの物理学. 物性研究, 91(1), 1–33.

西森秀稔. (1999). スピングラス理論と情報統計力学. 岩波書店.

Footnotes

1. 西森ライン ともいう．(Iba, 1999)，(西森秀稔, 1999, p. 55)など参照．

2. (横尾英俊, 2004, pp. 101–102)も参照．

3. (横尾英俊, 2004, p. 106) も参照．

4. (樺島祥介 and 杉浦正康, 2008, p. 28) も参照．

5. 充足可能性問題と違い，３項以上の相互作用を考えてもクラス P のままである．(Marc Mézard and Montanari, 2009, p. 246) や (樺島祥介 and 杉浦正康, 2008) も参照．

6. 例えば (Talagrand, 2011) など．

7. 従って，planted ensemble における \(\{y_{ij}\}\) は，同一の真値 \(x^*\) で繋がっているため，強い相関を持つ．この相関から \(x^*\) を読み解けるか？が逆に問題となっているのである．

8. 特に，信号処理などの情報科学的な設定で，この対応がつけやすい．というのも，一般の統計的な問題では，「スピングラスを生成する」部分に相当するような，データ生成過程に対する事前知識を持っていることが稀であり，モデル選択も重要なトピックに入るためである．一方で，スピングラス系と対応づけるとき，モデル選択は一般に射程には入らない．(Zdeborová and Krzakala, 2016, p. 456) も参照．一般の統計的問題を，どのようにしてスピングラスの planted ensemble と対応づけられるかについては，(Zdeborová and Krzakala, 2016, p. 468) 1.3.2 節を参照．

9. こうして生成されたスピングラス系を，planted ensemble と呼び，このシナリオを機械学習の訓練過程に準えて teacher-student scenario とも呼ぶのが (Zdeborová and Krzakala, 2016, p. 462) の用語である．これを (Iba, 1999, p. 3881) は符号理論に準えて，encoding-decoding scenario と呼ぶべき設定で解説している．(Marc Mézard and Montanari, 2009, p. 249) にも同様の通信に準えた記述がある．なお，最後の２つの文献では，事前分布 \(p(x)\) を一様分布に限っている．

10. 前稿 では，この \(x\) を \(x^*\) と表した．(Zdeborová and Krzakala, 2016) のように，これを lanted configuration または ground truth と呼ぶとわかりやすい．

11. この \(y\) は quenched disorder ともいう．quenched disorder が，ある信号 \(x\) とその通信 \(p(y|x)\) によって生成された系を，planted ensemble と考えるのである．そこで，(Zdeborová and Krzakala, 2016, p. 468) は planted disorder と呼んでいる．大変良い呼び名である．

12. (Zdeborová and Krzakala, 2016, p. 468) に多くの関連文献がまとめられている．

13. (Zdeborová and Krzakala, 2016, p. 476) も参照．

14. (Zdeborová and Krzakala, 2016, p. 475) 2.1 節も参照．(Krzakala et al., 2015, p. 13) の \([Z^n]_{\text{planted}}=\frac{[Z^{n+1}]_{\text{quenched}}}{[Z]_{\text{quenched}}}\) も関係するかもしれない．

15. (Marc Mézard and Montanari, 2009, p. 249) では \([-]\) ではなく \(\mathbb{E}\) で表されている．これを quenched average という．

16. (Zdeborová and Krzakala, 2016, pp. 480–2.5節)，(Marc Mézard and Montanari, 2009, pp. 102 5.4節) が詳しい．

17. 数学的な説明としては (Talagrand, 2011, p. 7) も参照．

18. このことは物理学にも進展を与えており，従来考えられなかった解析が進むことがあるという． (Krzakala et al., 2015, pp. 10 2.3節) や (Zdeborová and Krzakala, 2016, p. 483) 2.5.3 節 Quiet Planing を参照ください．

19. (Zdeborová and Krzakala, 2016, p. 483) 2.6 節，(Marc Mézard and Montanari, 2009, p. 253) 12.3.3 節．

20. (Zdeborová and Krzakala, 2016, p. 483) 2.6 節の興味深い説明方法．

21. (Marc Mézard and Montanari, 2009, p. 250) 12.3.1 節参照．

22. (Mattis, 1976) のモデルとも深い関連があるという．(Zdeborová and Krzakala, 2016, p. 474) も参照．ここでは planted SG model と呼ばれている．

23. すなわち，\(G(N,M)\)-Erdős–Rényi ランダムグラフ とする．

24. 従って，各 \(y_{ij}\) は \(x^*\) で条件付けると独立である．

25. (Zdeborová and Krzakala, 2016, p. 475)，(Iba, 1999, p. 3879)．

26. (Krzakala et al., 2015, p. 6) では MARG (Minimal Error Assignments Estimator) と呼ばれている．

27. また，平均場の設定では cavity method によって解ける．(Zdeborová and Krzakala, 2016, p. 475) も参照．

28. この同一視は，Nishimori ensemble と planted ensemble との同一視と論じることもできる (Krzakala et al., 2015, p. 12) 2.6 節．

29. (H. Nishimori, 1980) の報告である．(西森秀稔, 1999, pp. 53–)，(Iba, 1999, p. 3879) 式 (25)，(Marc Mézard and Montanari, 2009, p. 248) 式 (12.15) も参照．平均次数 \(c\) を持つランダムグラフ上の Edwards-Anderson モデルでは，\(M:=\lvert\mathcal{E}\rvert=c/2\) となる．

30. \(\beta^*\) は \(\rho\) の関数であることに注意．式 (2) 参照．

31. (西森秀稔, 1999, p. 55) も参照．

32. これは静的な RSB 相が存在しないことを言う．１次の相転移，動的な one-step RSB (d1RSB) 相などは見られることがある (Zdeborová and Krzakala, 2016, pp. 484 2.7節)．

33. (Iba, 1999, p. 3882) の時点で示唆されていた考え方である．

34. (Zdeborová and Krzakala, 2016, pp. 478 2.3節) も参照．

35. (Zdeborová and Krzakala, 2016, p. 479) 2.4節による素晴らしい洞察！