ベイズ統計学と統計物理学

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

本稿では全ての結果に数学的に厳密な証明をつけることを優先し，簡単なモデルを取り上げた．

一般のモデルと，スピングラス理論との大局観は，次稿を参照：

1 Bayes 推定

符号の誤り訂正，または denoising の文脈で Bayes 推定を考える．

雑音が加わる通信路から受け取った観測から真の信号を推定するというデノイジング問題は，Bayes 推定が自然に選好される格好の設定である．

1.1 デノイジング問題としての設定

情報源は無記憶で，確率分布 $p(x)dx$ に従うとし，通信路は，確率核 $p(y|x)dy$ に従うとする．

送信符号は１つの実数 $x^{\ast }\sim p(x)dx$ であったとし，この単一の入力 $x^{\ast }$ を $n$ 回独立に観測する： $$y_1,\cdots ,y_n\stackrel{\text{iid}}{\sim }p(y|x^{\ast })dy.$$

この観測を経たあと，送信符号 $x^{\ast }$ はいったい何だったのかを推定することを考えると，極めて自然に Bayes 推定が選択される．

純粋な解釈を持つ Bayes 推定

まず，何の観測もない場合，$x^{\ast }$ の確率分布は $p(x)dx$ である（設定上）．

しかし，すでに観測 $y_1,\cdots ,y_n$ を経ている．よってこの事象の上での $x^{\ast }$ の条件付き分布を計算すれば良いことになる： $$p(x|y_1,\cdots ,y_n)=\frac{p(\mathit{y}|x)p(x)}{p(\mathit{y})}$$ $$\begin{array}{}\text{(1)}& =\frac{{\displaystyle p(y_1|x)\cdots p(y_n|x)p(x)}}{{\displaystyle {\int }_{\mathbb{R}}p(y_1|x)\cdots p(y_n|x)p(x)dx}}\end{array}$$

こうして，誤り訂正符号の文脈では，Bayes 事前確率・事後確率が純粋に確率（または頻度）としての解釈を持つ．通常の統計的枠組みよりも仮定が多いが，その仮定の形式が Bayes 推定の形式にピッタリなのである．

信号処理と Bayesian formalism の類似性は (Iba, 1999, p. 3876)，(Zdeborová and Krzakala, 2016, p. 456) でも指摘されている．

また，統計力学をベイズ推定の特殊な場合とみなせるという見方は，(Jaynes, 1957) から始まる．¹

1.2 例：Delta-Gauss 混合

入力は $1/2$ の確率で $x=0$ だが，もう $1/2$ の確率で標準正規分布 $\mathrm{N}(0,1)$ に従うとする： $$p(x)dx=\frac{1}{2}{\delta }_0(dx)+\frac{1}{2}\mathrm{N}(0,1)(dx).$$ 通信路は加法的 Gauss 型であるとする： $$p(x,y)=\frac{1}{\sqrt{2\pi }}\exp (-\frac{(x-y{)}^2}{2}).$$ では真値を $x^{\ast }=1$ として，$n=10$ 回の観測データを生成してみる：

using Random

Random.seed!(123)
data = 1 .+ randn(10)
print(data)

[1.8082879284649667, -0.12207250811417336, -0.10463610232929588, 0.5830073648350667, 1.2875879806238557, 1.2298186980518677, 0.5782313356003073, -0.355590621101197, -0.08821851393628699, 1.7037583257923017]

愚直な計算から，$p(\mathit{y})$ は次の積分から得られる：

$$\begin{array}{rl}p(\mathit{y})& ={\int }_{\mathbb{R}}p(\mathit{y}|x)p(x)dx\\ & ={\int }_{\mathbb{R}}\prod _{i=1}^{n}p(y_i|x)p(x)dx\\ & =\frac{1}{2}\frac{1}{(2\pi {)}^{n+1}}{\int }_{\mathbb{R}}\exp (-\frac{1}{2}\sum _{i=1}^n(y_i-x{)}^2+x^2)dx\\ & +\frac{1}{2}\frac{1}{(2\pi {)}^n}\exp (-\frac{1}{2}\sum _{i=1}^n(y_i-x{)}^2)dx.\end{array}$$

これを実際に計算した結果は (Krazakala and Zdeborová, 2024, p. 117) で与えられている．

ここでは，邪教のような計算を啓示するのではなく，Julia と Turing を通じて計算する方法を紹介する (Storopoli, 2021)．

using Turing, Distributions

prior = MixtureModel([Normal(0.0, 1.0), Normal(0.0, 0.005)], [0.5, 0.5])

@model function mixed_normal_model(data)
    μ ~ prior
    for i in 1:length(data)
        data[i] ~ Normal(μ, 1)
    end
end

model = mixed_normal_model(data)

chain = sample(model, NUTS(), 100000)

using MCMCChains, Plots, StatsPlots

plot(chain[:μ], seriestype = :density, xlabel = "x*", ylabel = "Density", title = "Posterior Distribution", color = "#78C2AD")

vline!([1], color = :pink, linewidth = 2, label = "x^* = 1")

注（$x^{\ast }=0$ でのアトムについて）

$x^{\ast }=0$ に原子が存在する．

ここでは密度関数は滑らかに見えるが，実際には $x^{\ast }=0$ で不連続である．

これは，計算の都合上，${\delta }_0$ を $\mathrm{N}(0,0.005)$ で代用したためである．

1.3 MAP 推定量

定義 (maximum a posterior estimator)

$$\hat{x}:=\underset{x\in \mathbb{R}}{\mathrm{argmax}}p(x|y_1,\cdots ,y_n)$$ で定まる推定量 ${\mathbb{R}}^n\to \mathbb{R}$ を MAP 推定量 という．

例 1.2 などをはじめ，ほとんどの場面では良い推定量を与え，多くの場合の最初のチョイスとして適しているかもしれない．

しかし，例 1.2 をさらに変形することで，次のような事後分布が得られる状況は容易に想像がつく：

function f(x)
    if -1.8 < x < -1.6
        return 2.5
    elseif 0 < x < 1.5
        return 1
    else 
        return 0
    end
end

plot(f, -2, 2, size=(600, 400), legend=false, color="#78C2AD")

図 1

1.4 ベイズ最適推定量

図 1 の状況でも，たしかに１点のみを選ぶならば MAP 推定量で良いかもしれないが，$x\le 0$ である確率は $x\ge 0$ である確率よりも低いため，この意味では，$x\in [0,3/2]$ の範囲に推定量が収まっていた方が好ましいかもしれない．

推定量 ${\hat{x}}_n:{\mathbb{R}}^n\to \mathbb{R}$ を評価するには，何らかのアプリオリな 損失 の概念が必要である．これを損失関数 $L:{\mathbb{R}}^2\to \mathbb{R}$ という形で与える．

すると，損失の期待値が計算可能になり，これを 危険 という： $$R({\hat{x}}_n):=\mathrm{E}[L({\hat{x}}_n(\mathit{Y}),X)].$$

このリスクを最小化する推定量を ベイズ最適推定量，その際のリスクを ベイズリスク という．²

1.4.1 $l^2$-ベイズ最適推定量

命題

$L(x,y):=(x-y{)}^2$ と定める．このとき，事後平均 がベイズリスクを達成する： $$\hat{x}(\mathit{y}):={\int }_{\mathbb{R}}xp(x|\mathit{y})dx.$$

証明

図 1 の場合では，事後平均は約 $0.1$ で，かろうじて正になる．

1.4.2 $l^1$-ベイズ最適推定量

命題

$L(x,y):=|x-y|$ と定める．このとき，事後中央値 がベイズリスクを達成する．

証明

図 1 の場合では，事後中央値は $0.5$ となる．大変頑健な推定だと言えるだろう．

1.4.3 最適決定規則

今回の誤り訂正符号の文脈の目標は，$x^{\ast }$ の復元であることを思い出せば，今回の損失は $L(x,y)={\delta }_0(x-y)$ ととり，復号が成功する確率を最大とする推定量が「最良」と言うべきであろう： $$R({\hat{x}}_n)=\mathrm{P}[{\hat{x}}_n(\mathit{Y})=X]$$

これは結局 MAP 推定量 $${\hat{x}}_n:=\underset{x\in \mathbb{R}}{\mathrm{argmax}}p(x|\mathit{y})$$ で与えられることになる．

2 統計物理からの視点

真のシグナル $x^{\ast }\in \mathbb{R}$ を，Bayes 事後平均によって点推定する問題を，統計力学の観点から考察する．

次節 3 で，スパースな一般次元のベクトル $x^{\ast }\in {\mathbb{R}}^d$ を復元する問題に拡張する．

2.1 事後分布をある物理系の平衡分布と見る

ベイズの公式 (1) が与える事後分布 $p(x|\mathit{y})$ は，次の Boltzmann-Gibbs 分布として理解できる： $$p(x|\mathit{y})=\frac{e^{\log p(\mathit{y}|x)p(x)}}{p(\mathit{y})}$$ $$=\frac{e^{-H(x,\mathit{y})}}{Z(\mathit{y})},$$ $$H(x,\mathit{y}):=-\log p(\mathit{y}|x)-\log p(x),$$ $$Z(\mathit{y}):=p(y).$$

すなわち，Bayes 事後分布 $p(x|\mathit{y})$ は，$\mathbb{R}\times {\mathbb{R}}^n$ を配位空間に持ち，Hamiltonian $H(x,\mathit{y})$ を持つ正準集団の平衡分布と捉えることができる．

従って，Bayes 事後平均とは，この系に関する熱平均になる．加えて，MAP 推定量とは，この系に関する基底状態となる．

しかし，この系の，物理的な意義どころか，統計的な意義も定かではない．

2.2 もう一つの見方

今回，通信路は加法的に Gauss ノイズを加えるものとしたのであった： $$p(\mathit{y}|x)d\mathit{y}=\mathrm{N}(x,{\sigma }^2{)}^{\otimes n}(d\mathit{y})$$ この場合，前節 2.1 でみた方法の他に，事後分布 $p(x|\mathit{y})$ を次のように理解することもできる： $$p(x|\mathit{y})=\frac{e^{-H(x,\mathit{y})}}{Z(\mathit{y})},$$ $$H(x,\mathit{y}):=\frac{1}{2{\sigma }^2}\sum _{i=1}^n(x^2-2x{y}_i)-\log p(x),$$ $$Z(\mathit{y}):={\left(\frac{1}{(2\pi {\sigma }^2{)}^{\frac{n}{2}}}\frac{e^{-\frac{|\mathit{y}{|}^2}{2{\sigma }^2}}}{p(\mathit{y})}\right)}^{-1}.$$

この Hamiltonian $H$ により定まる系の分配関数 $Z(\mathit{y})$ は，情報源 $p(x)$ と Gauss 型通信路 $p(\mathit{y}|x)$ で与えられた観測 $\mathit{y}$ に関する周辺モデル $p(\mathit{y})$ と，完全にランダムなホワイトノイズ $\mathrm{N}(0,{\sigma }^2{)}^{\otimes n}$ との尤度比，または ベイズ因子 になっている．

式変形

$$\begin{array}{rl}p(x|\mathit{y})& =p(\mathit{y}|x)\frac{p(x)}{p(\mathit{y})}\\ & =\frac{p(x)}{p(\mathit{y})}\frac{1}{(2\pi {\sigma }^2{)}^{\frac{n}{2}}}{e}^{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(x-y_i{)}^2}\\ & =\frac{p(x)}{p(\mathit{y})}\frac{e^{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{y}_i^2}}{(2\pi {\sigma }^2{)}^{\frac{n}{2}}}{e}^{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(x^2-2x{y}_i)}\\ & =\frac{p(x)e^{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(x^2-2x{y}_i)}}{Z(\mathit{y})}\\ & =\frac{1}{Z(\mathit{y})}\exp (\log p(x)-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(x^2-2x{y}_i))\end{array}$$

さらに，この系 $H$ における自由エントロピーは，$p(\mathit{y})$ と $\mathrm{N}(0,{\sigma }^2{)}^{\otimes n}$ との間の KL 乖離度となっている： $$F_n:={\int }_{{\mathbb{R}}^n}\log \frac{p(\mathit{y})}{q(\mathit{y})}p(\mathit{y})d\mathit{y}=\mathrm{KL}(p,q).$$ ただし，$q$ は $\mathrm{N}(0,{\sigma }^2{)}^{\otimes n}$ の密度とした．

この系の他の物理量も，自由エネルギーと定数倍違うのみとなっている：

命題（エントロピーと相互情報量）³

この Hamiltonian $H$ を持つ系について，

1. エントロピー $H$ は次で与えられる：

   $$\begin{array}{rl}H(Y)& :=-{\int }_{{\mathbb{R}}^n}(\log p(\mathit{y}))p(\mathit{y})d\mathit{y}\\ & =\frac{n}{2}\log (2\pi {\sigma }^2)\\ & +\frac{1}{2{\sigma }^2}{\int }_{{\mathbb{R}}^n}|\mathit{y}{|}^{2}p(\mathit{y})d\mathit{y}-F_n.\end{array}$$

2. 相互情報量 $I$ は次で与えられる：

   $$\begin{array}{rl}I(X,Y)& :=\mathrm{KL}(p(x,y),p(x)p(y))\\ \\ & =\frac{n}{2{\sigma }^2}{\int }_{\mathbb{R}}{x}^{2}p(x)dx-F_n.\end{array}$$

特に，いずれも自由エネルギーの定数倍である

証明

1. の式変形は次のとおり： $$\begin{array}{rl}H(Y)& :=-{\int }_{{\mathbb{R}}^n}(\log p(\mathit{y}))p(\mathit{y})d\mathit{y}\\ & =-{\int }_{{\mathbb{R}}^n}p(\mathit{y})d\mathit{y}\log q(\mathit{y})-F_n\\ & =-{\int }_{{\mathbb{R}}^n}(-\frac{n}{2}\log (2\pi {\sigma }^2)-\frac{|\mathit{y}{|}^2}{2{\sigma }^2})p(\mathit{y})d\mathit{y}-F_n\\ & =\frac{n}{2}\log (2\pi {\sigma }^2)+\frac{n}{2{\sigma }^2}{\int }_{\mathbb{R}}{y}_i^{2}p(y_i)d{y}_i-F_n.\end{array}$$

2. 次の関係式を用いる： $$I(X,Y)=H(Y)-H(Y|X)$$ $H(Y)$ は 1. から判明しており，$H(Y|X)$ は次のように計算できる：

   $$\begin{array}{rl}H(Y|X)& =-{\int }_{{\mathbb{R}}^{n+1}}\log p(\mathit{y}|x)p(\mathit{y}|x)p(x)dxd\mathit{y}\\ & =-{\int }_{{\mathbb{R}}^{n+1}}\log (\frac{1}{(2\pi {\sigma }^2{)}^{\frac{n}{2}}}\exp (-\frac{1}{2{\sigma }^2}\sum _{i=1}^n(y_i-x{)}^2))p(\mathit{y}|x)p(x)dxd\mathit{y}\\ & ={\int }_{{\mathbb{R}}^{n+1}}(\frac{n}{2}\log (2\pi {\sigma }^2)+\frac{\sum _{i=1}^n(x-y_i{)}^2}{2{\sigma }^2})p(\mathit{y}|x)p(x)dxd\mathit{y}\\ & =\frac{n}{2}\log (2\pi {\sigma }^2)+\frac{1}{2{\sigma }^2}{\int }_{\mathbb{R}}({\int }_{{\mathbb{R}}^n}\sum _{i=1}^n(x-y_i{)}^{2}p(\mathit{y}|x)d\mathit{y})p(x)dx\\ & =\frac{n}{2}\log (2\pi {\sigma }^2)+\frac{n{\sigma }^2}{2{\sigma }^2}{\int }_{\mathbb{R}}p(x)dx\\ & =\frac{n}{2}\log (2\pi {\sigma }^2)+\frac{n}{2}.\end{array}$$

これと，$y_i$ には $x_i$ とこれと独立な分散 ${\sigma }^2$ のノイズが加わって得られる値であることから，次のように計算できる： $$\begin{array}{rl}I(X,Y)& =H(Y)-\frac{n}{2}\log (2\pi {\sigma }^2)-\frac{n}{2}\\ & =-F_n-\frac{n}{2}+\frac{n}{2{\sigma }^2}{\int }_{\mathbb{R}}{y}_i^{2}p(y_i)d{y}_i\\ & =-F_n-\frac{n}{2}+\frac{n}{2{\sigma }^2}({\sigma }^2+{\int }_{\mathbb{R}}{x}^{2}p(x)dx)\\ & =-F_n+\frac{n}{2{\sigma }^2}{\int }_{\mathbb{R}}{x}^{2}p(x)dx.\end{array}$$

2.3 西森対称性

命題 (Nishimori, 1980)⁴

$P:\mathbb{R}\to {\mathbb{R}}^n$ を確率核，$X^{\ast }\in \mathcal{L}(\mathrm{\Omega })$ は分布 $\nu \in \mathcal{P}(\mathbb{R})$ を持ち，$Y\in \mathcal{L}(\mathrm{\Omega };{\mathbb{R}}^n)$ の分布は $$\mu (dy)={\int }_{\mathbb{R}}\nu (dx)P(x,dy)$$ で定まるとする．ここで，$Y$ で条件づけた $X^{\ast }$ の確率分布を $P^{X|Y}$ とする： $$\nu (dx)={\int }_{{\mathbb{R}}^n}\mu (dy)P^{X|Y}(y,dx).$$ $$X^{(1)},\cdots ,X^{(k)}\stackrel{\text{iid}}{\sim }{P}^{X|Y}$$ を独立な確率変数列とすると，次が成り立つ：任意の $f\in {\mathcal{L}}_b({\mathbb{R}}^{n+k})$ について，

$$\begin{array}{rl}& \mathrm{E}[f(Y,X^{(1)},\cdots ,X^{(k)})]\\ & =\mathrm{E}[f(Y,X^{(1)},\cdots ,X^{(k-1)},X^{\ast })].\end{array}$$

$X^{(1)},\cdots ,X^{(k)}$ で表した確率変数の $P^{X|Y}$ に関する積分を Boltzmann 積分または熱平均と呼び，観測を作り出す過程 $(X^{\ast },Y)$ に関する積分を無秩序積分 (disorder expectation) または quenched average という．⁵

証明

この設定の下で，$(X^{\ast },Y)$ の結合分布が次の２通りで表せていることに注意： $$\nu (dx)P(x,dy)=\mu (dy)P^{X|Y}(y,dx).$$ 従って， $$\begin{array}{rl}& \nu (dx)P(x,dy)P^{X|Y}(y,d{x}^{(1)},\cdots ,d{x}^{(k)})\\ & =\mu (dy)P^{X|Y}(y,dx)P^{X|Y}(y,d{x}^{(1)},\cdots ,d{x}^{(k)})\end{array}$$ に関して $f(Y,X^{(1)},\cdots ,X^{(k)})$ の期待値を取ると，次のように計算できる： $$\begin{array}{rl}& \mathrm{E}[f(Y,X^{(1)},\cdots ,X^{(k)})]\\ & ={\int }_{{\mathbb{R}}^{n+k}}f(y,x^{(1)},\cdots ,x^{(k-1)},x^{(k)})P^{X|Y}(y,d{x}^{(1)})\cdots P^{X|Y}(y,d{x}^{(k)})\mu (dy)\\ & ={\int }_{{\mathbb{R}}^{n+k}}f(y,x^{(1)},\cdots ,x^{(k-1)},x)P^{X|Y}(y,d{x}^{(1)})\cdots P^{X|Y}(y,d{x}^{(k-1)})\nu (dx)P(x,dy)\\ & =\mathrm{E}[f(Y,X^{(1)},\cdots ,X^{(k-1)},X^{\ast })].\end{array}$$

確率核 $P$ にまつわる記法は次の記事も参照：

数学記法一覧

本サイトで用いる記法と規約

物理的な解釈

$P^{X|Y}$ に関する積分を $⟨-⟩$ で表すことで，何をどのように物理的に解釈しているかが明確になる： $$⟨X⟩=\mathrm{E}[X|Y].$$

この見方を採用すると，期待値を $$\mathrm{E}[f(Y,X^{(1)},\cdots ,X^{(k)})]={\mathrm{E}}^Y\left[⟨f(Y,X^{(1)},\cdots ,X^{(k)})⟩\right]$$ と二段階で捉えていることになる．右辺の外側の期待値は単に $Y$ のみに関してとっていることになる．

第 2.2 節で考えたモデル $H$ における Boltzmann 分布が $P^{X|Y}$ となり，平均 $⟨-⟩$ はこれに関する平均となる．

一方で，Hamiltonian $H$ にもランダム性が残っているのであり，これに関する平均が $(X^{\ast },Y)$ に関する平均に当たる．

こうして，ベイズ統計モデルはスピングラス系（特にランダムエネルギーモデル (Derrida, 1980)）と同一視できるようになる．

だが同時に，スピングラスのサンプリングを困難にする多谷構造も，ベイズ統計に輸入されるのである……．

スピングラスについては，次の記事も参照：

数学者のための統計力学１

Ising 模型とスピングラス

2.4 最小自乗誤差推定量

第 1.4.1 節で扱った最小自乗誤差推定量の自乗誤差は次のように計算できる：

命題（最小自乗誤差の表示）

$⟨X⟩:=\mathrm{E}[X|Y]$ と表す．事後平均推定量の自乗誤差は次のように表せる： $$\begin{array}{rl}\mathrm{MMSE}& :=\mathrm{E}[(X-\mathrm{E}[X|Y]{)}^2]\\ & =\mathrm{E}[X^2]-\mathrm{E}[⟨X{⟩}^2].\end{array}$$

証明

$$\begin{array}{rl}\mathrm{E}[\mathrm{V}[X|Y]]& =\mathrm{E}[(\mathrm{E}[X|Y]-X{)}^2]\\ & =\mathrm{E}[\mathrm{E}[X|Y{]}^2-2X\mathrm{E}[X|Y]+X^2]\\ & =\mathrm{E}[\mathrm{E}[X|Y{]}^2]-2\mathrm{E}[X\mathrm{E}[X|Y]]+\mathrm{E}[X^2]\\ & =\mathrm{E}[X^2]-\mathrm{E}[\mathrm{E}[X|Y{]}^2].\end{array}$$

この変形では，繰り返し期待値の法則 $$\begin{array}{rl}\mathrm{E}[X\mathrm{E}[X|Y]]& =\mathrm{E}[[X\mathrm{E}[X|Y]|Y]]\\ & =\mathrm{E}[\mathrm{E}[X|Y{]}^2]\end{array}$$ を西森の対称性の代わりに用いたことになる．

換言すれば，西森の対称性を証明したのと同様の方法を本命題にも適用したため，直接命題の適用は回避したことになる．

2.5 KL 乖離度の微分としての分散

次の定理は，相互情報量 $I$ と MMSE を結びつける定理であるため，(Guo et al., 2005) 以来，I-MMSE 定理 と呼ばれている．

命題（自由エネルギーによる特徴付け） (Guo et al., 2005)⁶

簡単のため，$n=1$ とする．このとき，$\beta :={\sigma }^{-2}$ に関して，次の式が成り立つ：

1. 自由エネルギー $F_1$ について， $$\frac{\partial F_1}{\partial \beta }=\frac{\mathrm{E}[⟨X{⟩}^2]}{2}.$$

2. 相互情報量 $I(X,Y)$ について，

   $$\begin{array}{rl}\frac{\partial I(X,Y)}{\partial \beta }& =\frac{\mathrm{E}[X^2]-\mathrm{E}[⟨X{⟩}^2]}{2}\\ & =\frac{\mathrm{MMSE}}{2}\end{array}$$

ただし，$⟨X⟩:=\mathrm{E}[X|Y]$ と定めた．

証明

$$\begin{array}{rl}\log \frac{p(y)}{q(y)}& =\frac{{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}{\int }_{\mathbb{R}}{e}^{-\frac{(x-y{)}^2}{2{\sigma }^2}}p(x)dx}}{\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{y^2}{2{\sigma }^2}}}\\ & ={\int }_{\mathbb{R}}{e}^{-\frac{x^2-2xy}{2{\sigma }^2}}p(x)dx.\end{array}$$

この $p(y)dy$ に関する積分を $\beta$ で微分すれば良いのであるが，$p(y)$ 自体が $\sigma$ に依存し，そのまま計算したのでは大変煩雑になる．

そこで，$y=\sigma z+x^{\ast }$ と変数変換をすることで，標準 Gauss 確率変数 $Z\sim {\gamma }_1$ と真値 $X^{\ast }$ は独立で，$\sigma$ も含まないから，次のように計算ができる： $$\begin{array}{rl}{F}_1(\beta )& ={\int }_{\mathbb{R}}\log \frac{p(y)}{q(y)}p(y)dy\\ & =\mathrm{E}[\log ({\int }_{\mathbb{R}}{e}^{-\frac{x^2-2xY}{2{\sigma }^2}}p(x)dx)]\\ & =\mathrm{E}[\log ({\int }_{\mathbb{R}}\exp (-\frac{x^2}{2{\sigma }^2}+\frac{xZ}{\sigma }+\frac{x{X}^{\ast }}{{\sigma }^2})p(x)dx)]\\ & =\mathrm{E}[\log ({\int }_{\mathbb{R}}\exp (-\frac{x^2\beta }{2}+xZ\sqrt{\beta }+x{X}^{\ast }\beta )p(x)dx)].\end{array}$$

こうして，最右辺の期待値に関する密度はもう $\beta$ に依存しないから，次のように微分が計算できる．ただし， $$\exp (-\frac{x^2\beta }{2}+xZ\sqrt{\beta }+x{X}^{\ast }\beta )p(x)dx$$ は $p(x|y)$ の定数倍，すなわち Gibbs 測度 $\frac{e^{-H(x,y)}}{Z(y)}dx$ の定数倍であることに注意して，これらに関する平均を引き続き $⟨-⟩:=\mathrm{E}[-|Y]$ で表すこととすると，

$$\begin{array}{rl}\frac{\partial F_1(\beta )}{\partial \beta }& =\mathrm{E}\left[\frac{{\displaystyle {\int }_{\mathbb{R}}(-\frac{x^2}{2}+\frac{xZ}{2\sqrt{\beta }}+x{X}^{\ast })e^{-\frac{x^2\beta }{2}+xZ\sqrt{\beta }+x{X}^{\ast }\beta }p(x)dx}}{{\displaystyle {\int }_{\mathbb{R}}\exp (-\frac{x^2\beta }{2}+xZ\sqrt{\beta }+x{X}^{\ast }\beta )p(x)dx}}\right]\\ & =-\frac{\mathrm{E}[⟨X^2⟩]}{2}+\frac{1}{2\sqrt{\beta }}\mathrm{E}[⟨X⟩Z]+\mathrm{E}[⟨X⟩X^{\ast }].\end{array}$$

$⟨X⟩$ が中に入っているのは，$\sigma [X^{\ast },Z]$ に関する条件付き期待値を $\mathrm{E}$ 内で取ったためと捉えられる．

まず，第二項は，Stein の補題 2.6 の系から， $$\begin{array}{rl}\frac{1}{2\sqrt{\beta }}\mathrm{E}[⟨X⟩Z]& =\frac{1}{2\sqrt{\beta }}\sqrt{\beta }(\mathrm{E}[⟨X^2⟩]-\mathrm{E}[⟨X{⟩}^2])\\ & =\frac{\mathrm{E}[⟨X^2⟩]}{2}-\frac{\mathrm{E}[⟨X{⟩}^2]}{2}\end{array}$$

第三項は，西森の対称性から， $$\begin{array}{r}\mathrm{E}[⟨X⟩X^{\ast }]=\mathrm{E}[⟨X{⟩}^2].\end{array}$$

以上を併せると， $$\frac{\partial F_1(\beta )}{\partial \beta }=\frac{\mathrm{E}[⟨X{⟩}^2]}{2}.$$

1. の主張も，$n=1$ のときは $$I(X,Y)=\frac{\beta }{2}{\int }_{\mathbb{R}}{x}^{2}p(x)dx-F_1$$ であったために従う： $$\begin{array}{rl}\frac{\partial I(X,Y)}{\partial \beta }& =\frac{\mathrm{E}[X^2]}{2}-\frac{\mathrm{E}[⟨X{⟩}^2]}{2}\\ & =\frac{\mathrm{MMSE}}{2}.\end{array}$$

$\mathrm{E}[⟨X{⟩}^2]$ は $q$ とも表され，スピングラスの 秩序パラメータ ともいう．⁷

$I$ の $\beta$ に関する二回微分を計算することより，$\beta$ に関する凸関数であることもわかる．

2.6 Stein の補題

命題 (Stein, 1972)

可積分な確率変数 $X\in {\mathcal{L}}^1(\mathrm{\Omega })$ について，次は同値：

1. $X$ の分布は標準Gaussである：$X\sim {\gamma }_1$．
2. 任意の $f\in C_b^1(\mathbb{R})$ について， $$\mathrm{E}[f^{\prime }(X)]=\mathrm{E}[Xf(X)]<\mathrm{\infty }.$$

証明

• (1)$\Rightarrow$(2)

  $f,f^{\prime }$ はいずれも有界としたから， $$\mathrm{E}[f^{\prime }(X)],\mathrm{E}[f(X)]<\mathrm{\infty }$$ が成り立つ．

  ${\gamma }_1$ の密度 $\varphi$ は ${\varphi }^{\prime }(x)=-x\varphi (x)$ を満たすことに注意すれば，部分積分により， $$\begin{array}{rl}\mathrm{E}[f^{\prime }(X)]& =-{\int }_{\mathbb{R}}f(x){\varphi }^{\prime }(x)dx\\ & ={\int }_{\mathbb{R}}f(x)x\varphi (x)dx=\mathrm{E}[f(X)X].\end{array}$$

• (2)$\Rightarrow$(1)

  $X$ は可積分としたから，特性関数 $\phi (u):=\mathrm{E}[e^{iuX}]$ は少なくとも $C^1(\mathbb{R})$-級で，その微分は $\varphi (x):=e^{iux}$ に関する仮定 $\mathrm{E}[{\varphi }^{\prime }(X)]=\mathrm{E}[X\varphi (X)]$ を通じて $$\begin{array}{rl}{\phi }^{\prime }(u)& =i\mathrm{E}[X{e}^{iuX}]=-u\mathrm{E}[e^{iuX}]\\ & =-u\phi (u),u\in \mathbb{R},\end{array}$$ と計算できる．

  この微分方程式は規格化条件 $\phi (0)=1$ の下で一意な解 $\phi (u)=e^{-\frac{u^2}{2}}$ を持つ．

系

$⟨X⟩:=\mathrm{E}[X|Y]$ とこれと独立な $Z\sim {\gamma }_1$ に関して，次が成り立つ：

$$\begin{array}{rl}\mathrm{E}[⟨X⟩Z]& =\mathrm{E}\left[\frac{\partial ⟨X⟩}{\partial Z}\right]\\ & =\sqrt{\beta }(\mathrm{E}[⟨X^2⟩]-\mathrm{E}[⟨X{⟩}^2])\end{array}$$

証明

最初の等号 $$\mathrm{E}[⟨X⟩Z]=\mathrm{E}\left[\frac{\partial ⟨X⟩}{\partial Z}\right]$$ は Stein の補題による．

続いて， $$⟨X⟩={\int }_{\mathbb{R}}xp(x|Y)dx$$ は $Y=\sigma Z+X^{\ast }$ を通じてのみ $Z$ に依存するから， $$\begin{array}{}\text{(2)}& \frac{\partial ⟨X⟩}{\partial Z}=\frac{\partial ⟨X⟩}{\partial Y}\frac{dY}{dZ}=\sigma \frac{\partial ⟨X⟩}{\partial Y}\end{array}$$ が成り立つ．あとは $⟨X⟩=\mathrm{E}[X|Y]$ の $Y$ に関する微分を計算すれば良い．

$$\frac{\partial p(y|x)}{\partial y}=-\frac{y-x}{{\sigma }^2}p(y|x).$$ また， $$p(y)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{\int }_{\mathbb{R}}{e}^{-\frac{(x-y{)}^2}{2{\sigma }^2}}p(x)dx$$ であったから， $$\begin{array}{rl}{p}^{\prime }(y)& =\frac{1}{\sqrt{2\pi {\sigma }^2}}{\int }_{\mathbb{R}}-\frac{y-x}{{\sigma }^2}{e}^{-\frac{(x-y{)}^2}{2{\sigma }^2}}p(x)dx\\ & =-{\int }_{\mathbb{R}}\frac{y-x}{{\sigma }^2}p(y|x)p(x)dx\\ & =-{\int }_{\mathbb{R}}\frac{y-x}{{\sigma }^2}p(x|y)p(y)dx\\ & =-\frac{y-⟨X⟩}{{\sigma }^2}p(y).\end{array}$$ $$\therefore \frac{p^{\prime }(Y)}{p(Y)}=\frac{⟨X⟩-Y}{{\sigma }^2}$$

に注意すれば，次のように計算できる：

$$\begin{array}{rl}\frac{\partial ⟨X⟩}{\partial Y}& =\frac{\partial }{\partial Y}{\int }_{\mathbb{R}}xp(x|Y)dx\\ & =\frac{\partial }{\partial Y}{\int }_{\mathbb{R}}x\frac{p(Y|x)p(x)}{p(Y)}dx\\ & ={\int }_{\mathbb{R}}x\frac{\partial }{\partial Y}\frac{p(Y|x)p(x)}{p(Y)}dx\\ & ={\int }_{\mathbb{R}}x\frac{\partial p(Y|x)}{\partial Y}\frac{p(x)}{p(Y)}dx\\ & +{\int }_{\mathbb{R}}x\left(\frac{\partial }{\partial Y}\frac{1}{p(Y)}\right)p(Y|x)p(x)dx\\ & =-{\int }_{\mathbb{R}}x\frac{Y-x}{{\sigma }^2}p(x|Y)dx\\ & -\frac{p^{\prime }(Y)}{p(Y)}{\int }_{\mathbb{R}}xp(x|Y)dx\\ & =-\frac{Y}{{\sigma }^2}⟨X⟩+\frac{⟨X^2⟩}{{\sigma }^2}\\ & -⟨X⟩\frac{⟨X⟩-Y}{{\sigma }^2}\\ & =\frac{1}{{\sigma }^2}(⟨X^2⟩-⟨X{⟩}^2).\end{array}$$

最後，式 ($\text{???}$) より， $$\begin{array}{rl}\frac{\partial ⟨X⟩}{\partial Z}& =\sigma \frac{\partial ⟨X⟩}{\partial Y}\\ & =\sqrt{\beta }(⟨X^2⟩-⟨X{⟩}^2).\end{array}$$

3 スパースベクトルの復号

スパースベクトルの信号推定問題を考える．ここまで，$x,x^{\ast }$ は $\mathbb{R}$ の点としてきたが，本節では，${\mathbb{R}}^d,d=2^N$ の one-hot ベクトルであるとする．

3.1 設定

真の信号 $x^{\ast }\in {\mathbb{R}}^d$ は，$d$ 次元の one-hot ベクトルであるとする．すなわち，次の集合 ${\mathrm{\Delta }}_d$ の元であるとする： $${\mathrm{\Delta }}_d:=\{x\in {\mathbb{Z}}^d\mid \parallel x{\parallel }_1=1\}.$$

加えて，${\mathrm{\Delta }}_d$ 上の一様分布に従うとする：$x^{\ast }\sim \mathrm{U}({\mathrm{\Delta }}_d)$．

これを分散 $\frac{{\sigma }^2}{N}$ を持った Gauss ノイズを通じて観測する： $$Y\sim {\mathrm{N}}_d(x^{\ast },\frac{{\sigma }^2}{N}{I}_d).$$

事前分布を $p(x)$，$Y$ の分布を $p(y)$ とすると，Bayes の定理より， $$\begin{array}{rl}p(x|y)& =\frac{p(x)}{p(y)}\prod _{i=1}^d\frac{e^{-\frac{(y_i-x_i{)}^2}{2{\sigma }^2/N}}}{\sqrt{2\pi {\sigma }^2/N}}\\ & =\frac{\prod _{i=1}^d\varphi (y_i;0,{\sigma }^2/N)}{p(y)}\\ & \times \frac{1}{2^N}\prod _{i=1}^d\exp (-\frac{x_i^2-2x_i{y}_i}{2{\sigma }^2/N})\end{array}$$

ただし，$\varphi (-;\mu ,\sigma ):=\frac{d{\mathrm{N}}_1(\mu ,\sigma )}{d{\ell }_1}$ を正規密度とした．

3.2 スピングラス系との同一視

この事後分布 $p(x|y)$ は，次の Hamiltonian $H$ に関する，逆温度 $\beta ={\sigma }^{-2}$ での Boltzmann 分布とみなせる：

$$\begin{array}{rl}p(x|y)& =\frac{1}{\mathcal{Z}}{e}^{-\beta H(x,y)}\\ H(x,y)& :=-N{\sigma }^2\log 2\\ & -\frac{N}{2}\sum _{i,j=1}^d{x}_i^{\ast }{x}_j^{\ast }\sqrt{(1-2y_i)(1-2y_j)}\end{array}$$

注

この Hamiltonian は非物理的なものであり，planted ensemble とも呼ばれる．(Murphy, 2023, p. 843) での clamped という表現と同じニュアンスである．詳しくは次項参照：

また，$H$ の表示については，$x^{\ast }\in {\mathrm{\Delta }}_d$ であるから，$i,j\in [d]$ と２つの和をとっているように見えるが，二つの添え字が一致している場合しか非零な値は取らず，結局 $$H(x,y)=-\frac{N}{2}\sum _{j=1}^d(2y_j-1)x_j+N{\sigma }^2\log 2$$ であることに注意．

なお，分配関数は $$\mathcal{Z}:=\frac{1}{2^N}\sum _{i=1}^d\exp (\frac{N}{2{\sigma }^2}(2y_i-1)),$$ と表される．

3.3 自由エネルギー密度の計算

系が用意されたら，統計力学はまず，代表的な物理量の熱力学極限を計算する．特に自由エネルギー密度は，熱力学極限 $N\to \mathrm{\infty }$ において自己平均性（確率論では集中性という性質）を示すことが期待される．

自由エネルギー密度 $\mathrm{\Phi }$ は，熱力学極限を通じて $$\mathrm{\Phi }(\beta ):=\underset{N\to \mathrm{\infty }}{lim}\frac{\mathrm{E}[\log \mathcal{Z}]}{N}$$ と定まる．

I-MMSE 定理（第 2.5 節）はこの多次元の $X$ に関しても有効であり， $${\mathrm{\Phi }}_N(\beta ):=\frac{\mathrm{E}[\log \mathcal{Z}]}{N}$$ に関して， $$\frac{\partial {\mathrm{\Phi }}_N(\beta )}{\partial \beta }=\frac{\mathrm{E}[|⟨X⟩{|}^2]}{2}$$ が成り立つ．

証明

まず有限の $N\in {\mathbb{N}}^{+}$ で計算する．

$$\frac{\partial {\mathrm{\Phi }}_N(\beta )}{\partial \beta }=\frac{1}{N}\mathrm{E}\left[\frac{1}{\mathcal{Z}}\frac{\partial \mathcal{Z}}{\partial \beta }\right]$$ の右辺を求めれば良い．

$$Y_i=X_i^{\ast }+\frac{\sigma }{\sqrt{N}}{Z}_i$$ であり，one-hot ベクトル $x\in {\mathrm{\Delta }}_d$ については $$x_j=x_j^2,|x{|}^2=1$$ でもあることに注意すれば，

$$\begin{array}{rl}\mathcal{Z}& =\sum _{i=1}^d{e}^{-H(x^{(i)},Y)}\\ & =\frac{1}{2^N}\sum _{i=1}^d\exp (-\frac{N\beta }{2}|x^{(i)}{|}^2+N\beta (Y|x^{(i)}))\\ & =\frac{1}{2^N}\sum _{i=1}^d\exp (-\frac{N\beta }{2}|x^{(i)}{|}^2+N(X^{\ast }|x^{(i)})\beta +(Z|x^{(i)})\sqrt{N\beta })\end{array}$$ $$\frac{\partial \mathcal{Z}}{\partial \beta }=\sum _i^d(-\frac{N}{2}|x^{(i)}{|}^2+N(X^{\ast }|x^{(i)})+\frac{\sqrt{N}}{2\sqrt{\beta }}(Z|x^{(i)}))e^{-H(x^{(i)},Y)}$$ $$\frac{1}{\mathcal{Z}}\frac{\partial \mathcal{Z}}{\partial \beta }=-\frac{N}{2}⟨|X{|}^2⟩+N⟨(X^{\ast }|X)⟩+\frac{\sqrt{N}}{2\sqrt{\beta }}⟨(Z|X)⟩$$ $$\frac{1}{N}\mathrm{E}\left[\frac{1}{\mathcal{Z}}\frac{\partial \mathcal{Z}}{\partial \beta }\right]=\mathrm{E}\left[⟨-\frac{⟨|X{|}^2⟩}{2}+⟨(X^{\ast }|X)⟩+\frac{⟨(Z|X)⟩}{2\sqrt{N\beta }}⟩\right]$$ これは１次元の場合の計算（第 2.5 節）と同様に， $$\frac{\partial {\mathrm{\Phi }}_N(\beta )}{\partial \beta }=\frac{\mathrm{E}[|⟨X⟩{|}^2]}{2}$$ と計算できる．

よって，$N\to \mathrm{\infty }$ の極限でも右辺が定数に収束し（右辺は $2^N$ 項和を含む），この種の関係式が成り立ち続けるならば，$\mathrm{\Phi }$ は $\beta$ の一次関数の形であるはずである．実際，次が示せる：

命題⁸

$\mathrm{\Delta }:={\sigma }^2$ の関数として，自由エネルギー密度 $\mathrm{\Phi }$ は次で定まる関数 $f:{\mathbb{R}}^{+}\to {\mathbb{R}}_{+}$ に一致する： $$f(\mathrm{\Delta }):=\{\begin{array}{ll}\frac{1}{2\mathrm{\Delta }}-\log 2& \mathrm{\Delta }\le {\mathrm{\Delta }}_c,\\ 0& \mathrm{\Delta }\ge {\mathrm{\Delta }}_c.\end{array}$$ $${\mathrm{\Delta }}_c:=\frac{1}{2\log 2}$$

証明

次節 3.4 では ${\mathrm{\Phi }}_N$ を $f$ によって上下から評価することで，数学的に厳密な証明を与える．ここでは，本ベイズモデルをランダムエネルギーモデルとみなし，レプリカ法によって計算した場合の証明の概略を付す．

$n$ 個のレプリカを複製した際の，それぞれの配置 $(i_1,\cdots ,i_n)\in [d{]}^n$ について足し合わせることで，$Z^n$ の disorder average を取る．

最終的に次の表示を得る： $$e^{nN(\log 2+\frac{\beta }{2})}\approx \int dQdM{e}^{Ns(Q,M)+N\beta (\sum _{a=1}^n{M}_a+\frac{1}{2}\sum _{a,b=1}^n{Q}_{a,b})}$$ $$\begin{array}{}\text{(3)}& =:\int dQdM{e}^{Ng(\mathrm{\Delta },Q,M)}.\end{array}$$ ただし，$M_a:={\delta }_{i_a,1}\in 2$ は磁化のベクトル，$Q_{ab}:={\delta }_{i_a,i_b}$ は overlap matrix と呼ばれる．

積分はこの $M_a,Q_{ab}$ の全体について実行され，同じ $M_a,Q_{ab}$ の値を取る配置の数を $$\mathrm{\#}(Q,M)=:e^{Ns(Q,M)}$$ と表した．

$N\to \mathrm{\infty }$ の極限では，式 (3) に対して Laplace 近似を実行すれば良い．

従って，$Q,M$ の構造のうち，特に支配的なものの特定に成功すれば，解が求まることになる．

最初の仮定として，レプリカ $i_1,\cdots ,i_d$ は交換可能で見分けがつかないはずだろう，という replica symmetric ansatz が考えられる．

このレプリカ対称性を仮定すると，次の３通りまでシナリオが絞られる：

1. 任意のレプリカは同一の状態にある：$i_a\equiv i\in [d]$．だが，正しいレプリカではない $i\ne 1$．

   このとき，$Q_{ab}\equiv 1,M_a\equiv 0$ となり，$s(Q,M)=\log 2$，かつ $g(\beta ,Q)=\log 2+n^2/\mathrm{\Delta }$．

   これは $N\to \mathrm{\infty }$ の極限で $n$ に関して線型ではなく，物理的な解が得られるとは思えず，レプリカ法も解析接続に失敗する．

2. 任意のレプリカは全て正しい状態にある：$i_a\equiv 1$．

   $Q_{ab}=M_a\equiv 1$ となり，$s(Q,M)=0,g(\beta ,Q)=n/\mathrm{\Delta }+n^2/2\mathrm{\Delta }$．

3. レプリカ内に少なくとも２つの違う状態がある：

   このとき，$g(\beta ,Q)=n/2\mathrm{\Delta }+n\log 2$．

２と３の場合から，次の２つが解の候補として回収できた： $$\mathrm{E}[Z^n]=e^{-nN(\log 2-\frac{\beta }{2})},$$ $$\mathrm{E}[Z^n]=0.$$

この２つは，次節 3.4 から導かれる厳密な結果に一致する．

最後，自由エネルギーの $\mathrm{\Delta }$ に関する凸性と解析性から，結論を得る．

3.4 自由エネルギーの上下評価

レプリカ法を回避し，数学的に厳密な証明を与えるには，次のように上下から評価することになる．

補題（下界）⁹

$${\mathrm{\Phi }}_N(\mathrm{\Delta })\ge f(\mathrm{\Delta })$$

証明

一般に下からの評価は，$Z_i$ に関する項をまとめて無視して良いために，簡単である．

$$Y_i=X_i^{\ast }+\frac{\sigma }{\sqrt{N}}{Z}_i,$$ $$Z_i\stackrel{\text{iid}}{\sim }{\mathrm{N}}_1(0,1),$$

であることから，$i^{\ast }$ を $X_{i^{\ast }}^{\ast }=1$ を満たす添字 $i^{\ast }\in [d]$ とすると，

$$\begin{array}{rl}\mathcal{Z}& =\frac{1}{2^N}\sum _{i=1}^d\exp (\frac{N{Y}_i}{{\sigma }^2}-\frac{N}{2{\sigma }^2})\\ & =\frac{1}{2^N}\sum _{i=1}^d\exp (\frac{N{X}_i^{\ast }}{{\sigma }^2}+\frac{\sqrt{N}}{\sigma }{Z}_i-\frac{N}{2{\sigma }^2})\\ & \ge \frac{1}{2^N}\exp (\frac{N}{{\sigma }^2}+\frac{\sqrt{N}}{\sigma }{Z}_{i^{\ast }}-\frac{N}{2{\sigma }^2})\\ & =\frac{1}{2^N}\exp (\frac{N}{2{\sigma }^2}+\frac{\sqrt{N}}{\sigma }{Z}_{i^{\ast }})\end{array}$$

と評価できる．

$$\log \mathcal{Z}\ge \frac{N}{2{\sigma }^2}+\frac{\sqrt{N}}{\sigma }{Z}_{i^{\ast }}-N\log 2.$$ $$\begin{array}{rl}{\mathrm{\Phi }}_N(\mathrm{\Delta })& =\frac{\mathrm{E}[\log \mathcal{Z}]}{N}\\ & \ge \frac{1}{N}(\frac{N}{2{\sigma }^2}-N\log 2)\\ & =\frac{1}{2\mathrm{\Delta }}-\log 2.\end{array}$$

これより，低温領域に於ては， $${\mathrm{\Phi }}_N\ge f\mathrm{on}(0,{\mathrm{\Delta }}_c)$$ が確認できた．

続いて， $$\begin{array}{rl}\frac{\partial {\mathrm{\Phi }}_N(\mathrm{\Delta })}{\partial \mathrm{\Delta }}& =\frac{\partial {\mathrm{\Phi }}_N(\mathrm{\Delta })}{\partial \beta }\frac{d\beta }{d\mathrm{\Delta }}\\ & =\frac{\mathrm{E}[|⟨X⟩{|}^2]}{2}(-\frac{1}{{\mathrm{\Delta }}^2})\le 0\end{array}$$ であることと， $$\underset{\mathrm{\Delta }\to \mathrm{\infty }}{lim}{\mathrm{\Phi }}_N(\mathrm{\Delta })=0$$ であることから，$[{\mathrm{\Delta }}_c,\mathrm{\infty })$ 上においても非負であることがわかる．

以上より， $${\mathrm{\Phi }}_N\ge f\mathrm{on}{\mathbb{R}}_{+}.$$

補題（上界）¹⁰

$${\mathrm{\Phi }}_N(\mathrm{\Delta })\le f(\mathrm{\Delta })+o(1)(N\to \mathrm{\infty })$$

証明

${\mathrm{\Phi }}_N$ の上界は，Boltzmann 分布 $p(x|y)$ に関する期待値に対して，Jensen の不等式を用いることで導かれる．このような不等式は annealed bound とも呼ばれる．

真値 $x^{\ast }$ とノイズ $z$ が確定している（従って，$x_{i^{\ast }}^{\ast }=1$ を満たす $i^{\ast }\in [d]$ も確定している）とすると， $$\begin{array}{rl}\mathcal{Z}& =\frac{1}{2^N}\sum _{i=1}^d\exp (-\frac{N\beta }{2}+N{x}_i^{\ast }\beta +z_i\sqrt{N\beta })\\ & =\frac{1}{2^N}(\exp (\frac{N\beta }{2}+z_{i^{\ast }}\sqrt{N\beta })+\sum _{i\ne i^{\ast }}\exp (-\frac{N\beta }{2}+z_i\sqrt{N\beta }))\end{array}$$ $$\log \mathcal{Z}=\log (\exp (\frac{N\beta }{2}+z_{i^{\ast }}\sqrt{N\beta }-N\log 2)+\sum _{i\ne i^{\ast }}\frac{1}{2^N}\exp (-\frac{N\beta }{2}\ast Z_i\sqrt{N\beta }))$$ と計算できる．凹関数 $\log$ に対する Jensen の不等式より， $$\begin{array}{rl}\mathrm{E}[\log \mathcal{Z}]& \le \mathrm{E}[\log (\exp (\frac{N\beta }{2}+Z_{i^{\ast }}\sqrt{N\beta }-N\log 2)\\ & +\sum _{i\ne i^{\ast }}{\mathrm{E}}_{Z_{-i^{\ast }}}[\frac{1}{2^N}\exp (-\frac{N\beta }{2}+Z_i\sqrt{N\beta })])]\\ & =\mathrm{E}[\log (\exp (\frac{N\beta }{2}+Z_{i^{\ast }}\sqrt{N\beta }-N\log 2)+\frac{2^{N-1}}{2^N})]\\ & \le \mathrm{E}[\log (\exp (\frac{N\beta }{2}+Z_{i^{\ast }}\sqrt{N\beta }-N\log 2)+1)]\\ & =\mathrm{E}[\log (e^{N(\frac{\beta }{2}-\log 2)}{e}^{Z_{i^{\ast }}\sqrt{N\beta }}+1)].\end{array}$$

最初の等号にて，$\xi \sim \mathrm{N}(\mu ,{\sigma }^2)$ の積率母関数が $$\mathrm{E}[e^{t\xi }]=\exp (\mu t+\frac{{\sigma }^2{t}^2}{2})$$ で表せることを用いた．

この $Z_{i^{\ast }}$ という確率変数は複雑に定まっており，これを直接議論することは後回しにする．

本補題の主張は，純粋に関数 $$g(z):=\exp (N(\frac{\beta }{2}-\log 2)+z\sqrt{N\beta })+1$$ の性質を考察するだけで従う．この関数 $g$ を用いると， $$\begin{array}{rl}{\mathrm{\Phi }}_N(\beta )& =\frac{\mathrm{E}[\log \mathcal{Z}]}{N}\\ & \le \frac{1}{N}\mathrm{E}[\log (g(Z_{i^{\ast }}))]\end{array}$$ と表せる．$g$ も $\log g$ も凸関数であるから， $$\begin{array}{rl}\log g(|z|)& \le \log g(0)+|z|\frac{d}{dz}\log g(|z|)\\ & =\log g(0)+\frac{g^{\prime }(|z|)}{g(|z|)}\\ & \le \log g(0)+|z|\sqrt{N\beta }\\ & =\log (e^{N(\frac{\beta }{2}-\log 2)}+1)+|z|\sqrt{N\beta }.\end{array}$$

これより， $$\begin{array}{rl}{\mathrm{\Phi }}_N(\beta )& \le \frac{1}{N}\mathrm{E}[\log (g(|Z_{i^{\ast }}|))]\\ & \le \frac{1}{N}\log (e^{N(\frac{\beta }{2}-\log 2)}+1)+\sqrt{\frac{\beta }{N}}\mathrm{E}[|Z_{i^{\ast }}|].\end{array}$$

よって，$Z_{i^{\ast }}$ が可積分であることさえ認めれば，$N\to \mathrm{\infty }$ のとき， $$\mathrm{\Delta }\ge {\mathrm{\Delta }}_c\iff \frac{\beta }{2}\le \log 2$$ のとき，$\log (e^{N(\frac{\beta }{2}-\log 2)}+1)\ge 0$ であり，そうでない場合は $$\log (1+e^x)\le xx\in {\mathbb{R}}_{+}$$ より， $${\mathrm{\Phi }}_N(\mathrm{\Delta })\le \frac{\beta }{2}-\log 2+o(1)(N\to \mathrm{\infty })$$ を得る．

3.5 解釈

$N\to \mathrm{\infty }$ の極限において，高温領域 $\mathrm{\Delta }>{\mathrm{\Delta }}_c$ において，最小自乗誤差（MMSE）は $1$ であり，何をどうしても復号することはできない．Gauss ノイズ $\mathrm{\Delta }={\sigma }^2$ が大きすぎるのである．

一方で，低温領域 $\mathrm{\Delta }<{\mathrm{\Delta }}_c$ において，${\partial }_{\beta }f=\frac{1}{2}$ であり，従って MMSE は $0$ になる．よって完全な誤りのない復号が可能であるはずである．

設定（第 3.1 節）が与えられたならば，立ち所に，$\mathrm{\Delta }$ が大きいほど復号が難しいことは予想がつく．しかし，ある閾値 ${\mathrm{\Delta }}_c$ に依存して，少なくとも $N\to \mathrm{\infty }$ の極限では，

• ２つの領域で全く異なる振る舞いをすること
• ２つの振る舞いのみに分類される（ある一定以上の確率で復号が可能である，などの中間状態がない）こと

は驚きである．

実は，高温領域 $\mathrm{\Delta }>{\mathrm{\Delta }}_c$ では，自由エネルギー $F_N$ が $0$ に指数収束する．$F_N$ とは，完全な Gauss ノイズ $$q(y)dy:={\mathrm{N}}_d(0,\frac{\mathrm{\Delta }}{N}{I}_d)$$ と $p(y)$ との KL 距離距離であったから，メッセージ $x^{\ast }$ を完全な雑音と見分けることが加速度的に難しくなっていくのである．

3.6 自由エネルギーのさらに鋭い評価

命題（KL 乖離度は指数収束する）¹¹

高温領域 $\mathrm{\Delta }>{\mathrm{\Delta }}_c$ において，ある $C>0$ が存在して，任意の $N\in {\mathbb{N}}^{+}$ について次が成り立つ：

$$\begin{array}{r}{F}_N(\mathrm{\Delta })=\mathrm{KL}(p(y)|q(y))\le e^{-CN}\end{array}$$

ただし，$p$ は観測信号 $Y\sim {\mathrm{N}}_d(X^{\ast },\frac{\mathrm{\Delta }}{N}{I}_d)$ の密度，$q$ は ${\mathrm{N}}_d(0,\frac{\mathrm{\Delta }}{N}{I}_d)$ の密度とした．

証明

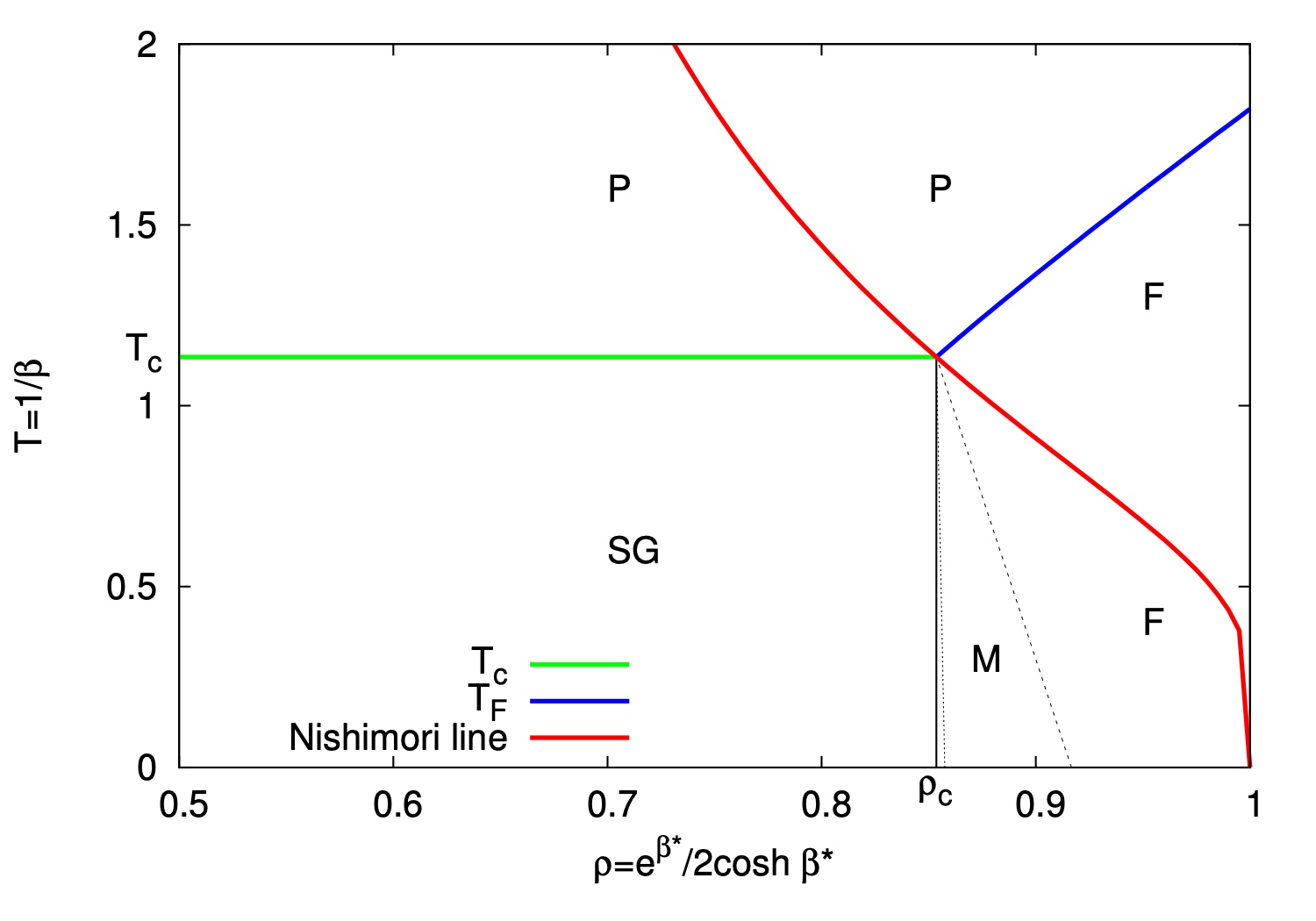
第 3.4 節で示した ${\mathrm{\Phi }}_N$ の上界評価では， $$\begin{array}{rl}{\mathrm{\Phi }}_N(\beta )& =\frac{\mathrm{E}[\log \mathcal{Z}]}{N}\\ & \le \frac{1}{N}\mathrm{E}[\log (\exp (N(\frac{\beta }{2}-\log 2)+Z_i^{\ast }\sqrt{N\beta })+1)]\end{array}$$ を得て，$Z_i^{\ast }$ の評価を回避したのであった．

これに正面から取り組むことで，高温領域 $\mathrm{\Delta }>{\mathrm{\Delta }}_c$ での ${\mathrm{\Phi }}_N$ の指数収束を示すことができる．

高温領域 $\mathrm{\Delta }>{\mathrm{\Delta }}_c$ では， $$f:=-\frac{\beta }{2}+\log 2>0$$ が成り立つ．

$Z_{i^{\ast }}$ は，まず $X^{\ast }$ によって条件付ければ $Z_{i^{\ast }}|X^{\ast }\sim \mathrm{N}(0,1)$ であるから， $$\begin{array}{rl}N{\mathrm{\Phi }}_N(\beta )& \le \mathrm{E}[\log (e^{-fN+Z_{i^{\ast }}\sqrt{N\beta }}+1)]\\ & ={\int }_{\mathbb{R}}\frac{e^{-\frac{z^2}{2}}}{\sqrt{2\pi }}\log (e^{-fN+z\sqrt{N\beta }}+1)dz\\ & =({\int }_{-\mathrm{\infty }}^R+{\int }_R^{\mathrm{\infty }})\frac{e^{-\frac{z^2}{2}}}{\sqrt{2\pi }}\log (e^{-fN+z\sqrt{N\beta }}+1)dz\end{array}$$ と分解すると，まず $(-\mathrm{\infty },R)$ 上の積分は $N\to \mathrm{\infty }$ に関して指数収束する．

実際，$R>0$ に対して $N\in {\mathbb{N}}^{+}$ を十分大きく取ることで，ある $ϵ>0$ が存在して $$-fN+z\sqrt{N\beta }\le -ϵfN$$ を満たすようにできるから，

$$\begin{array}{rl}& {\int }_{-\mathrm{\infty }}^R\frac{e^{-\frac{z^2}{2}}}{\sqrt{2\pi }}\log (e^{-fN+z\sqrt{N\beta }}+1)dz\\ & <{\int }_{\mathbb{R}}\frac{e^{-\frac{z^2}{2}}}{\sqrt{2\pi }}\log (e^{-ϵfN}+1)dz\\ & =\log (1+e^{-ϵfN})\le e^{-ϵfN}.\end{array}$$ 最後の不等式は $$\log (1+x)\le xx\in \mathbb{R}$$ による．

従って，あとは $(R,\mathrm{\infty })$ 上の積分が指数収束することを示せば良いが，再び $\log (1+x)\le x$ に注意して $$\begin{array}{rl}& {\int }_{\mathbb{R}}^{\mathrm{\infty }}\frac{e^{-\frac{z^2}{2}}}{\sqrt{2\pi }}\log (e^{-fN+z\sqrt{N\beta }}+1)dz\\ & \le {\int }_{\mathbb{R}}^{\mathrm{\infty }}\frac{1}{\sqrt{2\pi }}{e}^{-fN+z\sqrt{N\beta }-\frac{z^2}{2}}dz\\ & =e^{\frac{N\beta }{2}-fN}{\int }_{\mathbb{R}}^{\mathrm{\infty }}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(z-\sqrt{N\beta }{)}^2}{2}}dz\\ & =e^{\frac{N\beta }{2}-fN}\mathrm{P}[Z>R-\sqrt{N\beta }]\end{array}$$ と評価できるから，あとは $Z\sim {\gamma }_1$ の尾部確率が指数収束するかどうか（正確には劣 Gauss 性を持つかどうか）の問題に帰着する．

実はこれは yes である．中心化された確率変数の積率母関数が，ある $\sigma >0$ に関して $$\mathrm{E}[e^{\lambda \xi }]\le e^{\frac{{\lambda }^2{\sigma }^2}{2}}\lambda \in \mathbb{R}$$ を満たすことは，ある $\kappa >0$ が存在して $$\mathrm{P}[|\xi |\ge t]\le 2e^{-\frac{t^2}{2{\kappa }^2}}$$ を満たすことに同値になる．特に，$\Rightarrow$ 方向には $\kappa =\sigma$ ととれる．¹² ${\mathrm{\Phi }}_N$ の上界評価（第 3.4 節）で触れたように，（中心化された）Gauss 確率変数はこれを満たす．

よって， $$\begin{array}{rl}& e^{\frac{N\beta }{2}-fN}\mathrm{P}[Z>R-\sqrt{N\beta }]\\ & \le e^{\frac{N\beta }{2}-fN}{e}^{-\frac{(R-\sqrt{N\beta }{)}^2}{2}}\\ & =e^{\frac{N\beta }{2}-fN}{e}^{-\frac{R^2}{2}+\sqrt{N\beta }R-\frac{N\beta }{2}}\\ & =\exp (-\frac{R^2}{2}+\sqrt{N\beta }R-Nf).\end{array}$$

この最右辺，ある定数 $C>0$ が存在して，$e^{-CN}$ で抑えられる．

あるいは，任意の $N\in {\mathbb{N}}^{+}$ に対して $$R:=\sqrt{\frac{N}{\beta }}f-\delta \delta >0$$ と取ることで，$(-\mathrm{\infty },R),(R,\mathrm{\infty })$ 上の積分のそれぞれについて，同様の評価を得る．

以上より， $$\begin{array}{rl}{F}_N(\mathrm{\Delta })& =N{\mathrm{\Phi }}_N\\ & \le e^{-KN}.\end{array}$$

命題（劣 Gauss 確率変数の特徴付け）¹³

$X\in L(\mathrm{\Omega })$ を確率変数とする．このとき，次の４条件は同値で，さらに $\{K_1,\cdots ,K_5\}\subset {\mathbb{R}}^{+}$ はある $C\in \mathbb{R}$ が存在して，${\mathrm{\forall }}_{i,j\in [5]}{K}_j\le C{K}_i$ を満たすように取れる．

1. 尾部確率の評価：ある $K_1>0$ が存在して，¹⁴ $$\mathrm{P}[|X|\ge t]\le 2e^{-\frac{t^2}{K_1^2}},t\ge 0.$$
2. $L^p$-ノルムの評価：ある $K_2>0$ が存在して， $$\parallel X{\parallel }_{L^p}\le K_2\sqrt{p},p\ge 1.$$
3. $X^2$ の積率母関数の $0$ の近傍での評価：ある $K_3>0$ が存在して， $$|\lambda |\le \frac{1}{K_3}\Rightarrow \mathrm{E}[e^{{\lambda }^2{X}^2}]\le e^{K_3^2{\lambda }^2}.$$
4. $X^2$ の積率母関数のある1点での値：ある $K_4>0$ が存在して， $$\mathrm{E}\left[e^{\frac{X^2}{K_4^2}}\right]\le 2.$$
5. さらに，$X$ が中心化されている場合，次とも同値：ある $K_5>0$ が存在して， $$\mathrm{E}[e^{\lambda X}]\le e^{K_5^2{\lambda }^2},\lambda \in \mathbb{R}.$$

以上の同値な条件を満たす確率変数 $X$ を 劣 Gauss (sub-Gaussian) という．

3.7 まとめ

大変単純化された設定 toy model であったが，比例的高次元極限 $N\to \mathrm{\infty }$ において，厳密に示せる相転移を示す模型である．

すなわち，ただ一つの非零成分 $1$ に対して，ノイズの分散 ${\sigma }^2$ が $(2\log 2{)}^{-1}$ より大きいかどうかで，これが復号可能かどうかが決まる．

この $2\log 2$ という値は (Donoho and Johnstone, 1994) が universal threshold と呼ぶ値の例であり，ランダムエネルギーモデルのスピングラス相転移境界と対応する．¹⁵

一般のモデルでは，この臨界温度の値は不明である上に，$\mathrm{\Delta }>{\mathrm{\Delta }}_c$ の高温領域での効率的な推定法が見つかっていない場合も多い．

このような，高次元統計推測の問題においては，統計物理学，特にスピングラス理論の知見が活発に応用されて，漸近極限における相図の解明，統計計算手法の開発が目指されている．

Schematic representation of a typical high-dimensional inference problem from (Zdeborová and Krzakala, 2016, p. 466)

4 終わりに

第 3 節において，統計力学の知見は，レプリカ法などの計算手法を通じて，$N\to \mathrm{\infty }$ における漸近極限として，「大規模な確率分布から平均値を計算するための”ツールボックス”」(樺島祥介, 2003) として働いている．

大自由度系では，次元に関して計算量が指数約に爆発してしまう．平衡統計力学の歴史はこの問題との戦いの歴史である，と言っても過言ではない．(樺島祥介 and 杉浦正康, 2008, p. 22)

References

Derrida, B. (1980). Random-energy model: Limit of a family of disordered models. Phys. Rev. Lett., 45, 79–82.

Donoho, D. L., and Johnstone, I. M. (1994). Ideal spatial adaptation by wavelet shrinkage. Biometrika, 81(3), 425–455.

Guo, D., Shamai, S., and Verdu, S. (2005). Mutual information and minimum mean-square error in gaussian channels. IEEE Transactions on Information Theory, 51(4), 1261–1282.

Iba, Y. (1999). The Nishimori line and Bayesian statistics. Journal of Physics A: Mathematical and General, 32(21), 3875.

Jaynes, E. T. (1957). Information theory and statistical mechanics. Phys. Rev., 106, 620–630.

Krazakala, F., and Zdeborová, L. (2024). Statistical physics methods in optimization and machine learning.

Krzakala, F., Zdeborova, L., Angelini, M. C., and Caltagirone, F. (2015). Statistical physics of inference and bayesian estimation.

Mézard, M., and Montanari, A. (2009). Information, physics, and computation. Oxford University Press.

Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. MIT Press.

Nishimori, H. (1980). Exact results and critical properties of the ising model with competing interactions. Journal of Physics C: Solid State Physics, 13(21), 4071.

Shalev-Shwartz, S., and Ben-David, S. (2014). Understanding machine learning: From theory to algorithms. Cambridge University Press.

Stein, C. (1972). A Bound for the Error in the Normal Approximation to the Distribution of a Sum of Dependent Random Variables. Stanford University. Retrieved from https://purl.stanford.edu/jc818sv7483

Storopoli, J. (2021). Bayesian statistics with julia and turing.

Vershynin, R. (2018). High-dimensional probability,Vol. 47. Cambridge University Press.

Zdeborová, L., and Krzakala, F. (2016). Statistical physics of inference: Thresholds and algorithms. Advances in Physics, 65(5), 453–552.

樺島祥介. (2003). コトの物理学：誤り訂正符号を例として. 日本物理学会誌, 58(4), 239–246.

樺島祥介, and 杉浦正康. (2008). コトの物理学. 物性研究, 91(1), 1–33.

西森秀稔. (2005). 相転移・臨界現象の統計物理学,Vol. 35. 培風館.

Footnotes

1. (Zdeborová and Krzakala, 2016, p. 467) も参照．

2. (Shalev-Shwartz and Ben-David, 2014, p. 25) や (Krazakala and Zdeborová, 2024, p. 119) に倣った．

3. (Krazakala and Zdeborová, 2024, p. 122)．

4. (Zdeborová and Krzakala, 2016, p. 464)，(Krazakala and Zdeborová, 2024, p. 123) 定理13，(Iba, 1999, pp. 3876–3877) などで扱われている．西森ライン上のみで見られる性質であるため，西森対称性と呼ぶ．西森ラインについては 次項 も参照．

5. (Mézard and Montanari, 2009, p. 249) や (Iba, 1999, p. 3876) などでは thermal average と quenched average の用語が採用されている．

6. (Krazakala and Zdeborová, 2024, p. 124) 定理14．

7. (西森秀稔, 2005, p. 123)なども参照．

8. (Krazakala and Zdeborová, 2024, p. 125) 定理15，(樺島祥介 and 杉浦正康, 2008, p. 14) なども参照．証明は (Krazakala and Zdeborová, 2024, p. 133) 7.B 節 を参考にした．

9. (Krazakala and Zdeborová, 2024, p. 125)補題８．

10. (Krazakala and Zdeborová, 2024, p. 126)補題９．

11. (Krazakala and Zdeborová, 2024, p. 132)補題10．

12. (Vershynin, 2018, p. 25)命題2.5.2など．

13. (Vershynin, 2018, p. 25)命題2.5.2．

14. この定数2は，1よりも真に大きい定数ならばなんでも良い．(Vershynin, 2018, p. 27)注2.5.3 も参照．

15. (Krzakala et al., 2015, p. 8) また p.16 も参照すべし．