ベイズ階層多ハザードモデル

前稿

Zig-Zag サンプラーについては次の記事も参照：

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1 ベイズ階層多ハザードモデル

1.1 多ハザードモデルの表現力

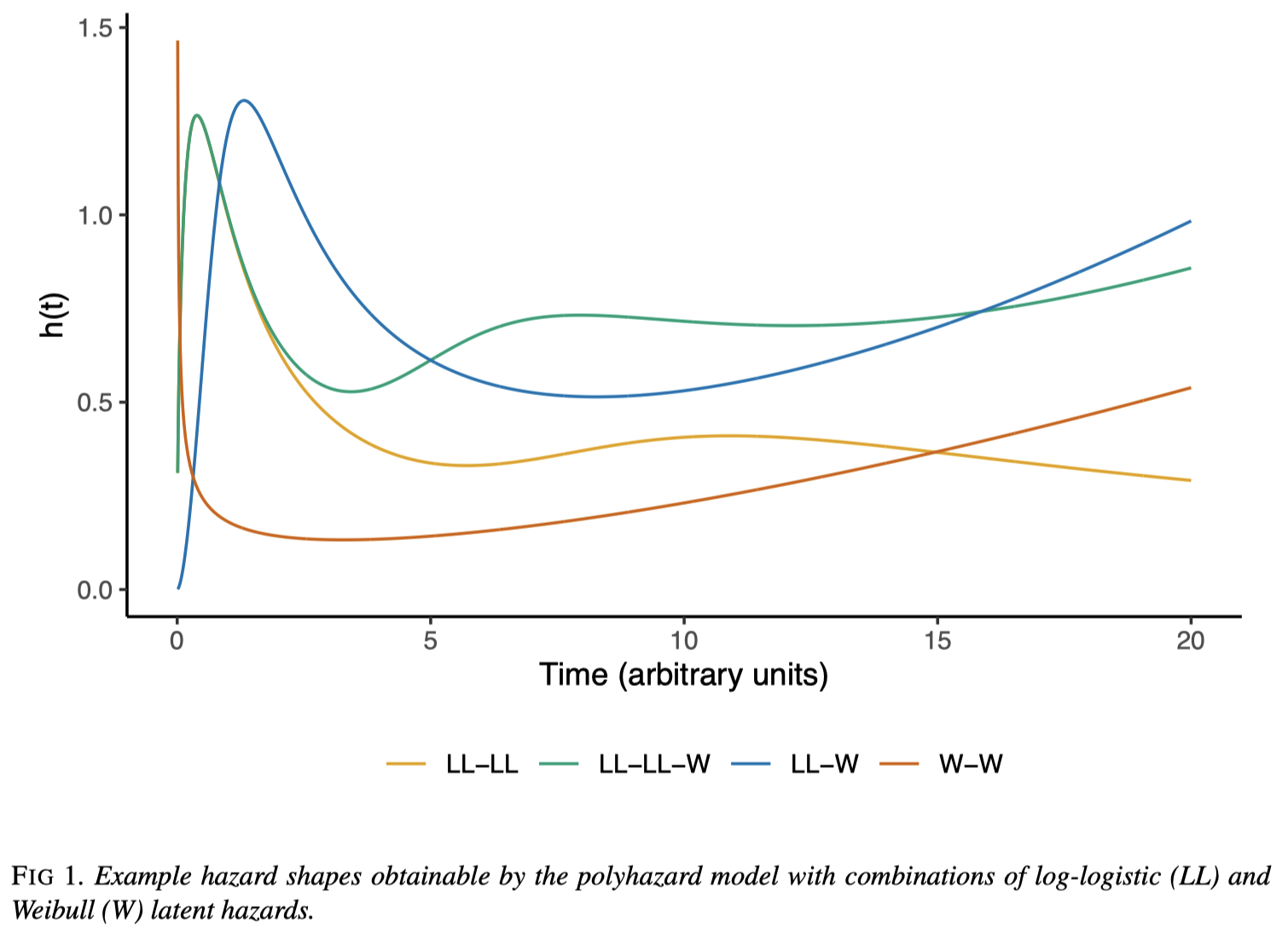
Polyhazard model もハザード関数をモデリングするが， \[ h_Y(y)=\sum_{j=1}^Kh_j(y) \] という形でモデリングし，個々の \(h_j\) にパラメトリックな仮定をおく．

仮に \(h_j\) として，形状母数 \(\nu>0\) と位置母数 \(\mu:=\alpha^{-\nu}>0\) を持つ Weibull 分布 \(\mathrm{W}(\nu,\mu)\) のハザード関数 \[ h_{\mathrm{W}}(y):=\mu\nu y^{\nu-1} \] と対数ロジスティック分布 \(\mathrm{LL}(\nu,\mu)\) のハザード関数 \[ h_{\mathrm{LL}}(y):=\frac{\left(\frac{\nu}{\mu}\right)\left(\frac{y}{\mu}\right)^{\nu-1}}{1+\left(\frac{y}{\mu}\right)^\nu} \] の２つのみを考えたとしても，複数のパラメトリックモデルを足し合わせることで驚異的な表現力を達成することができる．

(Hardcastle et al., 2024, p. 5) より．

1.2 ベイズ階層多ハザードモデル

(Hardcastle et al., 2024) では HTA への応用を念頭に，完全なベイズ階層多ハザードモデルの推定を試みている．

1.2.1 第１階層

各個別要因 \(k\in[K]\) の形状母数 \(\nu_k\) と位置母数 \(\mu_k\) に階層構造 \[ \log(\nu_k)=\alpha_k\sim\mathrm{N}(0,\sigma_\alpha^2) \tag{1}\] \[ \log(\mu_k)=\beta_{k,0}+\sum_{j\in\left\{j\in[p]\mid\gamma_{kj}=1\right\}}x_j\beta_{k,j},\qquad\beta_{k,0}\sim\mathrm{N}(0,\sigma_{\beta_0}^2) \tag{2}\] を考える．ただし，\(\gamma_{k,j}\in2\) は共変量 \(x_j\) が \(k\in[K]\) 番目の部分モデルに参加するかどうかを決める指示変数とする．

式 (2) で残っているパラメータ \(\beta_{k,j}\;(j\in[p])\) には \[ \beta_{k,j}\sim(1-\omega)\delta_0+\omega\operatorname{N}(0,\sigma_\beta^2) \] と spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) を仮定し，変数選択を促進する．選択された変数については \(\gamma_{k,j}=1\) とする．

以降，\(\theta_k=(\nu_k,\mu_k)\) とし，\((K,\gamma,\theta)\) を本モデルのパラメータと理解する（\(K\) の事前分布は後述 1.2.3）．

1.2.2 第２階層

\(\sigma_\alpha^2=2,\sigma_{\beta_0}^2=5\) は固定してしまうと，\(\phi:=(\omega,\sigma_\beta)\) がハイパーパラメータとして残っている．これには \[ \omega\sim\operatorname{Beta}(a,b) \] \[ \sigma_\beta\sim\operatorname{HalfCauchy}(0,1) \] という事前分布をおき，\(a=b=4\) と固定する．

前者はモデルのサイズについて Beta-二項分布を仮定することに等価である (3.1 節 Ley and Steel, 2009)．後者は (Gelman, 2006), (Polson and Scott, 2012) の推奨の通りである．

1.2.3 \(\mathcal{P}(E)\) 上の事前分布

実はまだ第一階層のパラメータが残っている．ハザードの数 \(K\) と \(h_k\) の関数形をどうするかである．

ここでは Weibull 分布 \(\mathrm{W}(\nu,\mu)\) と対数ロジスティック分布 \(\mathrm{LL}(\nu,\mu)\) の２つ \[ D=\{\mathrm{W}(\nu,\mu),\mathrm{LL}(\nu,\mu)\} \] から等確率で \[ K\sim\mathrm{Pois}_{>0}(\xi) \] 個選ぶこととする．

ハイパーパラメータ \(\xi\) については，(Hardcastle et al., 2024) では \(\xi=2\) としている．その根拠の１つに \[ \operatorname{P}[K\ge5]\approx0.061 \] を満たす性質が，実際の応用で５つ以上の競合リスクが存在する場面は稀であることに整合することを挙げている：

2 PDMP によるベイズ競合リスク分析

2.1 はじめに

前節で定義されたモデルのパラメータ空間 \[ (K,D,\gamma,\phi,\theta) \] 上での事後分布サンプリングを行うことを考える．\(\phi=(\omega,\sigma_\beta)\) はハイパーパラメータである．

基本的には \(\theta=(\theta_k)=(\nu_k,\mu_k)\) の事後分布サンプリングを考えるのであるが，\(K,\gamma\) の如何によって \(\theta\) の次元が変化する．

加えて \(D\) の如何によって尤度が変化するから，Poisson 点過程の強度関数に解析的な上界が見つかるはずもないため，Automatic Zig-Zag (Corbella et al., 2022) と Concave-Convex PDMP (Sutton and Fearnhead, 2023) を組み合わせて用いる．

2.2 \(\theta\) の Zig-Zag サンプリング

polyhazard model の標準的なサンプラーには Gibbs サンプラーや NUTS サンプラーがあり得るが，いずれも複数の次元の間を飛び回れるように拡張するには，空間の間の跳躍をうまく設計する必要がある．

この点で Zig-Zag サンプラーは従来のサンプリング法と対等であるが，今回の設定には多峰性の懸念も存在する．

というのも，\(D\) によって指定される分布は互いに交換可能であるため，混合モデリングにおける label switching problem (Jasra et al., 2005) 同様に事後分布は必然的に多峰性（対称性）を帯びるはずである．

多峰性への対処という点では，Zig-Zag サンプラーに軍配が上がるはずである (Andrieu and Livingstone, 2021)．

2.3 ハイパーパラメータ \(\phi\) のサンプリング

\((\theta,\phi)\) 上から結合分布を Zig-Zag サンプリングすることも可能であるが，\(\theta\) は \(\phi\) に依存するため，事後分布は強い相関構造を持つと予想される．

一方でこの条件付き構造は Gibbs サンプラーの発想で有効に利用したいものである．これには Zig-Zag within Gibbs (Sachs et al., 2023) を用いることができる．

この方法によれば，ハイパーパラメータ \(\phi=(\omega,\sigma_\beta)\) を固定した下で他の変数をサンプリングすることになる．この設定では次に論じるように変数選択の指示変数 \(\gamma\) に対する効率的なシミュレーション法も導く．

2.4 変数選択 \(\gamma\) のサンプリング

一般にベイズ変数選択は \(\gamma\) のような指示変数のサンプリングに問題を帰着させる方法 (Zanella, 2020) が state-of-the-art とされる．

しかし各 \(\gamma\in 2^{Kp}\) に対応するモデルの（周辺）尤度の計算が困難な場面は多く，特に今回の生存モデルはその一例である (Liang et al., 2023)．

しかし Zig-Zag サンプラーでは \(\{\beta_{k,j}=0\}\) のなす部分空間を通過する際に一定の確率でランダムな時間ここに囚われることで，自然な形で trans-dimensional なサンプリングが可能になることが (Chevallier et al., 2023), (Bierkens et al., 2023) により同時に提案されている．

この際 \(\{\beta_{k,j}=0\}\) から脱出する確率は時刻や位置に依らず（ハイパーパラメータ \(\omega\) の下で）一定であり，一様な Poisson 点過程のシミュレーションにより実現される．この意味で Zig-Zag サンプラーによる変数選択は，周辺尤度の計算を回避した効率的な計算法を提供する．

2.5 \(K,D\) のサンプリング

ここでは birth-death-swap 過程を用いる．というのも，３つの Poisson 点過程 \(\Lambda^b,\Lambda^d,\Lambda^s\) を用いて，これが到着するごとに確率核 \(q_b,q_d,q_s\) に従って新たなハザード関数の追加・消去・取り替えが起こる．

取り替えは必ずしも必要がないが，これの追加により多峰性の問題 2.2 が解決され，サンプラーの収束が改善されるという．

birth-death 過程は次の詳細釣り合い条件を満たせば良い： \[ \Lambda^b(t)\pi(\theta,D,K)q_b(u)=\Lambda^d(t)\pi(\theta',D',K')q_d(u'). \]

この方法は Zig-Zag within Gibbs (Sachs et al., 2023) の Gibbs 核を，(Green, 1995) の超次元跳躍核に取り替えていることに等しい．

3 文献紹介

Andrieu, C., and Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: Beyond the reversible scenario. The Annals of Statistics, 49(4), 1958–1981.

Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Chevallier, A., Fearnhead, P., and Sutton, M. (2023). Reversible jump PDMP samplers for variable selection. Journal of the American Statistical Association, 118(544), 2915–2927.

Corbella, A., Spencer, S. E. F., and Roberts, G. O. (2022). Automatic Zig-Zag Sampling in Practice. Statistics and Computing, 32(6), 107.

Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis, 1(3), 515–534.

Green, P. J. (1995). Reversible jump markov chain monte carlo computation and bayesian model determination. Biometrika, 82(4), 711–732.

Hardcastle, L., Livingstone, S., and Baio, G. (2024). Averaging polyhazard models using piecewise deterministic monte carlo with applications to data with long-term survivors.

Jasra, A., Holmes, C. C., and Stephens, D. A. (2005). Markov Chain Monte Carlo Methods and the Label Switching Problem in Bayesian Mixture Modeling. Statistical Science, 20(1), 50–67.

Ley, E., and Steel, M. F. J. (2009). On the effect of prior assumptions in bayesian model averaging with applications to growth regression. Journal of Applied Econometrics, 24(4), 651–674.

Liang, X., Livingstone, S., and Griffin, J. (2023). Adaptive MCMC for bayesian variable selection in generalised linear models and survival models. Entropy, 25(9).

Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.

Polson, N. G., and Scott, J. G. (2012). On the Half-Cauchy Prior for a Global Scale Parameter. Bayesian Analysis, 7(4), 887–902.

Sachs, M., Sen, D., Lu, J., and Dunson, D. (2023). Posterior Computation with the Gibbs Zig-Zag Sampler. Bayesian Analysis, 18(3), 909–927.

Sutton, M., and Fearnhead, P. (2023). Concave-Convex PDMP-based Sampling. Journal of Computational and Graphical Statistics, 32(4), 1425–1435.

Zanella, G. (2020). Informed proposals for local MCMC in discrete spaces. Journal of the American Statistical Association, 115(530), 852–865.