ベイズ階層多ハザードモデル
Zig-Zag サンプラーによるモデル平均法
次稿
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1 生存時間と競合リスクの解析
1.1 はじめに
医療経済学 などにおける 医療技術評価 (HTA: Health Technology Assessment) とは，新たな医療技術を臨床試験で評価し，リスクやコストを勘案して新技術の既存法との効果や安全性を評価・比較する 決定理論的な枠組み である．
この枠組みでは非負確率変数 \(Y\) に対して，例えば次のような平均の計算が必要になる： \[ \operatorname{E}[Y]=\int^\infty_0S_Y(y)\,dy,\qquad S_Y(y):=\operatorname{P}[Y\ge y]. \tag{1}\]
医療技術評価の文脈において \(Y\) は被験者のイベントまでの時間 (time-to-event) を表す確率変数で，\(S_Y\) は \(Y\) の 生存（割合）関数 といい，\(Y\) の分布関数 \(F_Y\) と次の関係を持つ： \[ S_Y(y)=1-F_Y(y). \]
平均 (1) を計算するためには，観測の打ち切りを乗り越えて \(S_Y\) を \([0,\infty)\) 全域で推定する必要があり，そのためにはベイズ手法が有望視されている（第 1.5 節）．
1.2 生存時間解析とは
イベントまでの時間 \(Y\) の生存関数 \(S_Y\) を推定する問題は 生存時間解析 (survival analysis) または信頼性解析として知られ，ほとんど統計学の起源と同時に始まる長い歴史を持つ．1
共変量 \(X\) の生存時間 \(Y\) への影響を調べる際には，生存関数 \(S_Y\) の代わりに ハザード関数 （または瞬間故障率，死亡率） \[ h(y):=\frac{f(y)}{S(t)}=-\frac{d \log S(y)}{d t},\qquad f(y)=F'(y)=-S'(y), \] もモデリングの対象になる．ただし \(f\) は \(Y\) の確率密度関数とした．
ハザード関数 \(h\) は，被験者の生存割合が \(S(y)\) である段階での，次の単位時間でのイベント発生率を表す．ハザード関数が判れば，生存関数は \[ S(y)=\exp\left(-\int^y_0h(t)\,dt\right) \] によって復元される．
さらに究極の目標として，生存時間 \(Y\) に影響を与える共変量 \(X\) の成分を特定することがある．この際に用いるモデルを 競合リスクモデル という（第 1.7 節）．
競合する \(K\) 個のリスク要因がそれぞれハザード \(h_1,\cdots,h_K\) を持つとき，イベント発生時刻 \(Y\) のハザードは和 \[ h_Y(y)=\sum_{j=1}^Kh_j(y) \] で与えられる．これを 多ハザード模型 (Polyhazard model)（第 1.6 節），\(h_i\) を 原因別ハザード という．
1.3 生存関数推定
1.3.1 欠測の問題
生存時間解析における最大の問題は観測の 打ち切り (censoring) である．
換言すれば，ほとんどの生存時間データでは種々の理由で被験者が脱落し，追跡終了時点以降はイベントの発生を確認できないのである．
そこで，５割生存時間 (MST: Median Survival Time) を代わりに推定対象としたり，ある打ち切り時刻 \(T>0\) までの区間のみに限って \(S:[0,T]\to[0,1]\) を推定することが考えられた．
1.3.2 パラメトリックモデル
\(S_Y\) をパラメトリックな分布族の中から推定することが考えられる．
この場合，形状母数 \(\nu>0\) によってハザード関数の増加・減少を柔軟にモデリングできる Weibull 分布 \(\mathrm{W}(\nu,\alpha)\) または (Rosin and Rammler, 1933) の分布 \[ f(x;\nu,\alpha)=\frac{\nu}{\alpha}\left(\frac{x}{\alpha}\right)^{\nu-1}\exp\left(-\left(\frac{x}{\alpha}\right)^\nu\right)1_{\left\{x>0\right\}},\qquad\alpha>0,\nu>0, \] \[ h(t)=\frac{\nu}{\alpha}\left(\frac{t}{\alpha}\right)^{\nu-1}1_{\left\{t>0\right\}} \] をはじめとして，Gamma 分布，対数正規分布，対数ロジスティック分布分布，パレート分布など，極値分布の指数変換様の分布族が用いられる．
1.3.3 ノンパラメトリックモデル
これには (Kaplan and Meier, 1958) や (Cutler and Ederer, 1958) の方法が古来より有名である．
1.4 回帰
1.4.1 ハザードの回帰
生存時間解析の主な目的は，生存曲線の正確な描画というより，生存時間を決定する要因の特定にある．
(Cox, 1972) はベースとなる生存関数 \(S_0\) (baseline survival curve) を局外母数として，\(S\) と \(S_0\) の関係をパラメトリックにモデリングする．
より正確には，ハザード関数 \(h\) のベース \(h_0\) からの比の対数を，線型な予測子 \[ \log \frac{h(y)}{h_0(y)}=X^\top\beta+\epsilon \] によってモデリングする．
一般にハザードの比を \[ h(y|x)=h_0(y)c(X^\top\beta) \] とモデリングするものを 乗法的ハザードモデル といい，特に \(c=\exp\) と取った場合を Cox の 比例ハザードモデル (Cox’s proportional hazard model) とも呼ばれる．
この方法は，打ち切りデータへの対処が簡便になることが美点である．
1.4.2 生存時間の回帰
生存時間 \(Y\) の対数を直接 \[ \log Y=\mu+\beta^\top X+\epsilon \] によってモデリングする方法は 加速故障時間モデル (AFT: Accelerated Failure Time Model) (Wei, 1992) と呼ばれる．
このモデルはハザード関数に，\(h_0\) を \(x=0\) の場合のハザード関数として \[ h(y|x)=e^{-\beta^\top x}h_0(ye^{-\beta^\top x}), \] という乗法的な仮定をおいていることに相当する．
1.5 生存関数推定再論
一方で医療行為の社会的な影響も考える HTA の目標を達成するためには，式 (1) のような量を計算する必要がある．
そのためには，生存曲線の推定と同時に打ち切り時点以降の外挿もできるようなモデルを考える必要があるが，Kaplan-Meier 法などのノンパラメトリック法は（現状）この用途には用いることができない．
表現力が高いパラメトリックモデルをベイズ推定することが，非常に魅力的な解決策として考えられ，実際 NICE のガイドラインでも推奨されている (Latimer, 2011)．
その際の魅力的なモデルに polyhazard model (Berger and Sun, 1993), (Louzada-Neto, 1999) がある．
(Latimer, 2013) では現状の HTA 分析では，生存時間モデルに対してモデル検証・モデル選択が不十分であることに警鐘が鳴らされている．
polyhazard model のような階層モデルを効率的にベイズ推定・モデル平均化ができるような MCMC 法が開発されることは，このモデル検証の手続きを自動化したり，より手軽にするために非常に重要である．
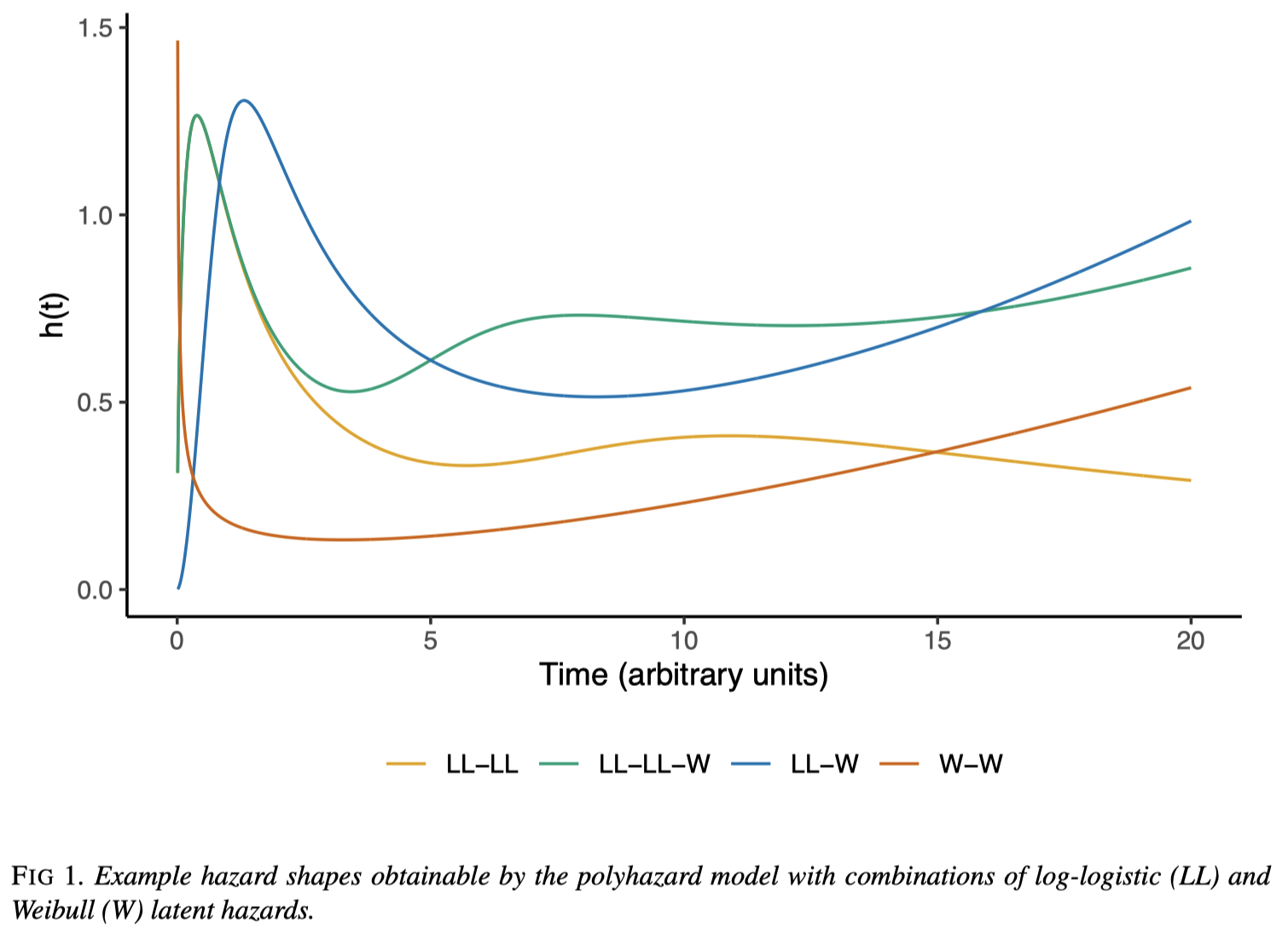
1.6 多ハザードモデルの表現力
Polyhazard model もハザード関数をモデリングするが， \[ h_Y(y)=\sum_{j=1}^Kh_j(y) \] という形でモデリングし，個々の \(h_j\) にパラメトリックな仮定をおく．
仮に \(h_j\) として，形状母数 \(\nu>0\) と位置母数 \(\mu:=\alpha^{-\nu}>0\) を持つ Weibull 分布 \(\mathrm{W}(\nu,\mu)\) のハザード関数2 \[ h_{\mathrm{W}}(y):=\mu\nu y^{\nu-1} \] と対数ロジスティック分布 \(\mathrm{LL}(\nu,\mu)\) のハザード関数 \[ h_{\mathrm{LL}}(y):=\frac{\left(\frac{\nu}{\mu}\right)\left(\frac{y}{\mu}\right)^{\nu-1}}{1+\left(\frac{y}{\mu}\right)^\nu} \] の２つのみを考えたとしても，複数のパラメトリックモデルを足し合わせることで驚異的な表現力を達成することができる．
1.7 競合リスク解析
1.7.1 モデルの解釈
polyhazard モデルでは各 \(h_k\) の前に係数がついていない点には注意が必要である．
各 \(h_k\) は実在の原因のハザードを表しており，各被験者は同時に \(K\) 個のリスクに晒されているというモデルである（第 1.2 節）．
このようなモデルを 競合リスクモデル (competing risk model) ともいう．
例えば，心臓の移植後のハザード曲線はバスタブ曲線の形を持ち，少なくとも２つの別々の競合するリスク要因が存在することが窺える (Demiris et al., 2015)．
1.7.2 競合リスクモデリング
しかし，リスク因子はほとんどの場合観測できず，潜在変数となる．\(K\) の数も不確実である．
このような識別不可能なモデルは，階層モデルとしてベイズ推論を実行することが向いていると言えるかも知れない．
さらに発展的なモデルにはマルチステートモデルもある (齋藤哲雄 and 室谷健太, 2023), (Saito and Murotani, 2024)．
1.8 ベイズ階層多ハザードモデル
(Hardcastle et al., 2024) では HTA への応用を念頭に，完全なベイズ階層多ハザードモデルの推定を試みている．ここではそのモデルの詳細を紹介する．
1.8.1 第１階層
各個別要因 \(k\in[K]\) の形状母数 \(\nu_k\) と位置母数 \(\mu_k\) に階層構造 \[ \log(\nu_k)=\alpha_k\sim\mathrm{N}(0,\sigma_\alpha^2) \tag{2}\] \[ \log(\mu_k)=\beta_{k,0}+\sum_{j\in\left\{j\in[p]\mid\gamma_{kj}=1\right\}}x_j\beta_{k,j},\qquad\beta_{k,0}\sim\mathrm{N}(0,\sigma_{\beta_0}^2) \tag{3}\] を考える．ただし，\(\gamma_{k,j}\in2\) は共変量 \(x_j\) が \(k\in[K]\) 番目の部分モデルに参加するかどうかを決める指示変数とする．
残っているパラメータ \(\beta_{k,j}\;(j\in[p])\) には \[ \beta_{k,j}\sim(1-\omega)\delta_0+\omega\operatorname{N}(0,\sigma_\beta^2) \] と spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) を仮定し，変数選択を促進する．
以降，\(\theta_k=(\nu_k,\mu_k)\) とし，\((K,\gamma,\theta)\) を本モデルのパラメータとする．
1.8.2 第二階層
\(\sigma_\alpha^2=2,\sigma_{\beta_0}^2=5\) は固定してしまうと，\(\phi:=(\omega,\sigma_\beta)\) がハイパーパラメータとして残っている．これには \[ \omega\sim\operatorname{Beta}(a,b) \] \[ \sigma_\beta\sim\operatorname{HalfCauchy}(0,1) \] という事前分布をおく．
前者はモデルのサイズについて Beta-二項分布を仮定することに等価である (3.1 節 Ley and Steel, 2009)．後者は (Gelman, 2006), (Polson and Scott, 2012) の推奨の通りである．
1.8.3 \(\mathcal{P}(E)\) 上の事前分布
実はまだ第一階層のパラメータが残っている．ハザードの数 \(K\) と \(h_k\) の関数形をどうするかである．
ここでは Weibull 分布 \(\mathrm{W}(\nu,\mu)\) と対数ロジスティック分布 \(\mathrm{LL}(\nu,\mu)\) の２つ \[ D=\{\mathrm{W}(\nu,\mu),\mathrm{LL}(\nu,\mu)\} \] から等確率で \[ K\sim\mathrm{Pois}_{>0}(\xi) \] 個選ぶこととする．
ハイパーパラメータ \(\xi\) については，(Hardcastle et al., 2024) では \(\xi=2\) としている．この根拠は \[ \operatorname{P}[K>4]\approx0.061 \] であることとしている．
1.8.4 部分的な階層モデル
元々部分的に階層化された多ハザードモデルは広く考えられていた．
(Demiris et al., 2015) は \(K\in\{1,2,3,4\}\) の poly-Weibull モデルを推定し，その適合具合を比較した．
(Benaglia et al., 2015) では \(K=2\) に限ったが，bi-Weibull モデルと bi-Gompertz モデルを推定し，視覚化手法によりモデルの適合具合を比較した．
このように個別のモデルを推定してベストのものを選び出す方法は，モデルの仮定を緩和して多くの変数を動かすようにすればするほど難しくなっていく．
例えば分布族も種々のものを考え，\(K\in\{1,2,3,4\}\) のいずれも考えるとなると，推定すべき個別のモデルは乗法的に増加していく．
そこで (Negrín et al., 2017) は，モデルを「比較」して「選択」するよりもむしろ，ベイズモデル平均 (BMA: Bayesian Model Averaging) を用いることでモデルの不確実性を考慮しつつ最終的なモデルを得ることを提案した．
しかし，そのモデルは \(K=2\) の Weibull 分布族にのみ限っていた．
2 PDMP によるベイズ競合リスク分析
(Hardcastle et al., 2024) では完全なベイズ階層 polyhazard モデルに対するサンプラーを Zig-Zag サンプラーに基づいて構成している．ここではこれを紹介する．
2.1 課題
完全なベイズ階層多ハザードモデルが考えられていなかったことは，次の３つの問題によると考えられる：
そこで局外母数 \((K,D,\gamma,\phi)\) と推定対象 \(\theta\in\mathbb{R}^{2K+\lvert\gamma\rvert_1}\) のサンプリングに，多峰性分布につよい Zig-Zag サンプラーを用いる．
2.2 \(\theta\) の Zig-Zag サンプリング
Zig-Zag サンプラーについては次の記事も参照：
No matching items
モデルが複雑であることに加えて尤度が変動することもあり，Poisson 点過程に対する解析的に上界が見つかるはずもないため，Automatic Zig-Zag (Corbella et al., 2022) を Concave-Convex PDMP (Sutton and Fearnhead, 2023) で修正して用いる．
続きは次稿参照：
No matching items
3 文献紹介
生存時間解析について (武冨奈菜美 and 山本和嬉, 2023) は網羅的で入門的な日本語文献である．
(西川正子, 2008) は競合リスクモデルに焦点を当てた日本語文献である．(齋藤哲雄 and 室谷健太, 2023), (Saito and Murotani, 2024) はマルチステートモデルも扱っている．(森満, 2016) は医学者による説明が与えられている．
本項は (Hardcastle et al., 2024) を大きく参考にした．
References
Benaglia, T., Jackson, C. H., and Sharples, L. D. (2015). Survival extrapolation in the presence of cause specific hazards. Statistics in Medicine, 34(5), 796–811.
Berger, J. O., and Sun, D. (1993). Bayesian analysis for the poly-weibull distribution. Journal of the American Statistical Association, 88(424), 1412–1418.
Corbella, A., Spencer, S. E. F., and Roberts, G. O. (2022). Automatic Zig-Zag Sampling in Practice. Statistics and Computing, 32(6), 107.
Cox, D. R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society. Series B (Methodological), 34(2), 187–220.
Cutler, S. J., and Ederer, F. (1958). Maximum utilization of the life table method in analyzing survival. Journal of Chronic Diseases, 8(6), 699–712.
Demiris, N., Lunn, D., and Sharples, L. D. (2015). Survival extrapolation using the poly-weibull model. Statistical Methods in Medical Research, 24(2), 287–301.
Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper). Bayesian Analysis, 1(3), 515–534.
Hardcastle, L., Livingstone, S., and Baio, G. (2024). Averaging polyhazard models using piecewise deterministic monte carlo with applications to data with long-term survivors.
Kaplan, E. L., and Meier, P. (1958). Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53(282), 457–481.
Latimer, N. R. (2011). NICE DSU technical support document 14: Undertaking survival analysis for economic evaluations alongside clinical trials–estrapolation with patient-level data. National Institute for Health; Care Excellence. Retrieved from https://www.sheffield.ac.uk/nice-dsu/tsds/survival-analysis
Latimer, N. R. (2013). Survival analysis for economic evaluations alongside clinical trials—extrapolation with patient-level data: Inconsistencies, limitations, and a practical guide. Medical Decision Making, 33(6), 743–754.
Ley, E., and Steel, M. F. J. (2009). On the effect of prior assumptions in bayesian model averaging with applications to growth regression. Journal of Applied Econometrics, 24(4), 651–674.
Louzada-Neto, F. (1999). Polyhazard models for lifetime data. Biometrics, 55(4), 1281–1285.
Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.
Negrín, M. A., Nam, J., and Briggs, A. H. (2017). Bayesian solutions for handling uncertainty in survival extrapolation. Medical Decision Making, 37(4), 367–376.
Polson, N. G., and Scott, J. G. (2012). On the Half-Cauchy Prior for a Global Scale Parameter. Bayesian Analysis, 7(4), 887–902.
Rosin, P., and Rammler, E. (1933). The law governing the fineness of powdered coal. Journal of the Institute of Fuel, 7, 29–36.
Saito, T., and Murotani, K. (2024). Competing risks and multistate modelsin oncology clinical trials. Japanese Journal of Biometrics, 45(1), 37–65.
Sutton, M., and Fearnhead, P. (2023). Concave-Convex PDMP-based Sampling. Journal of Computational and Graphical Statistics, 32(4), 1425–1435.
Wei, L. J. (1992). The accelerated failure time model: A useful alternative to the cox regression model in survival analysis. Statistics in Medicine, 11(14-15), 1871–1879.
森満. (2016). 専門医に必要な統計の知識と研究デザイン. 日本耳鼻咽喉科学会会報, 119(7), 989–992.
武冨奈菜美, and 山本和嬉. (2023). 生存時間解析・信頼性解析のための統計モデル. 日本統計学会誌, 52(2), 69–112.
西川正子. (2008). 生存時間解析における競合リスクモデル. 計量生物学, 29(2), 141–170.
齋藤哲雄, and 室谷健太. (2023). マルチステートモデルの理論とがん臨床研究への応用. 日本統計学会誌, 52(2), 221–267.
Footnotes
(武冨奈菜美 and 山本和嬉, 2023) は Halley の生命表や Daniel Bernoulli の競合リスク解析の例を挙げている．生命表については ベイズ計算の稿 も参照．↩︎
位置母数 \(\mu:=\alpha^{-\nu}>0\) の変換により第 1.3.2 節のハザード関数と見た目が異なることに注意．↩︎