動き出す次世代サンプラー・区分確定的モンテカルロ

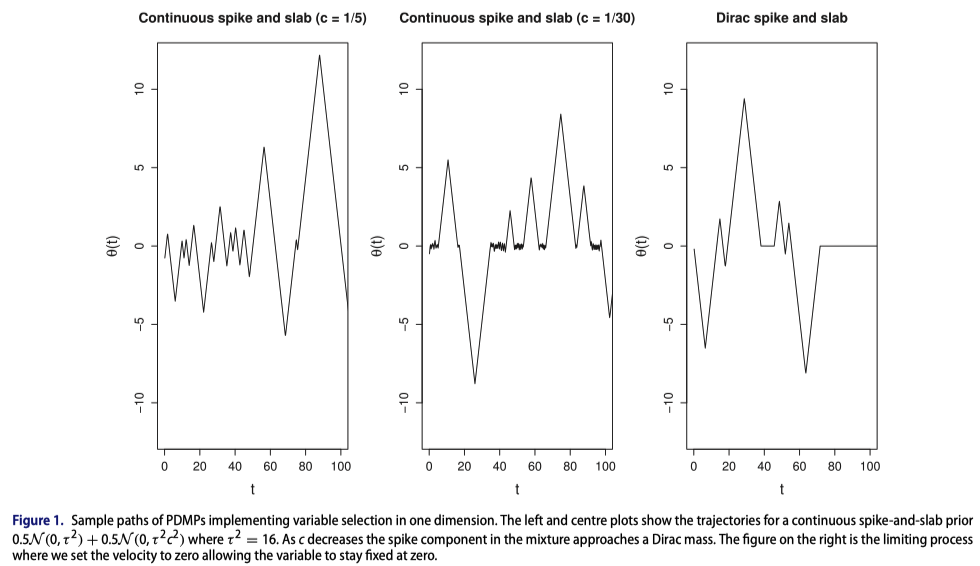
この研究の着想は極めて自然なものだと感じていた．実際 (Chevallier ほか, 2023) でも，Sticky PDMP ではないが，可逆ジャンプ PDMP が「極限として得られる」ことのシミュレーション上の言及がある：

Sticky PDMP (Bierkens ほか, 2023) や可逆ジャンプ PDMP がある種の極限過程としてみなせることは誰もが直感的に捉えていたことであろう．

新年に入り，指導教員と初めての研究ディスカッションをやってみようという初回であった１月15日のことであった．すでに Forward ECMC (Michel ほか, 2020) の解析について１時間半ほど議論し，方針が見えてきたところだったが，「研究として面白いだろうが，計算に時間がかかるだろう．より手早くできるテーマをもう一つ考えた方が良いかもしれない」という言葉をもらった．

ほとんど終わりかけの雑談のようなつもりで，Sticky PDMP は明らかに連続 spike-and-slab 分布の slab 幅に関する収束極限なのであるから，これを厳密に導出したいと前から思っていたことを話した．

すると思いがけず，これが Multiscale Analysis (Pavliotis と Stuart, 2008) の例であることが瞬時に指摘された．

その集は特別研究員や海外派遣プログラム，学生研究発表会などたくさんの申請・書類提出で忙しかったが，すぐに Sticky PDMP は必ずしも極限にならないことが理解された．極限ならば可逆になるはずである．

参考文献

Bierkens, J., Grazzi, S., Meulen, F. van der, と Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Chevallier, A., Fearnhead, P., と Sutton, M. (2023). Reversible Jump PDMP Samplers for Variable Selection. Journal of the American Statistical Association, 118(544), 2915–2927.

Michel, M., Durmus, A., と Sénécal, S. (2020). Forward Event-Chain Monte Carlo: Fast Sampling by Randomness Control in Irreversible Markov Chains. Journal of Computational and Graphical Statistics, 29(4), 689–702.

Pavliotis, G. A., と Stuart, A. M. (2008). Multiscale Methods: Averaging and Homogenization. Springer New York.

引用

BibTeX

@online{博文2025,
  author = {博文, 司馬},
  title = {動き出す次世代サンプラー・区分確定的モンテカルロ},
  date = {2025-02-17},
  url = {https://162348.github.io/posts/2025/Publications/Sticky.html},
  langid = {ja}
}

引用方法

博文司馬. (2025, February 17). 動き出す次世代サンプラー・区分確定的モンテカルロ.