ベイズ計算とは何か | About Bayesian Computation

History of Bayesian Computation (Martin et al., 2023, p. 4)

1 「ベイズ計算」の「ベイズ」とは何者か？

賭博，生命保険，確率論この三つの間には，その発生に切っても切れない因縁がある．この点を明確に摘出することは，統計学の黎明を知るのに不可欠であろう． (北川敏男, 1949)

de Moivre を彼の著 Approximation に，また Bayes を彼の定理に導いた原因は，純然たる数学的なものというよりも，神学的及び社会学的のものであった． (Pearson, 1926)

1.1 ベイズまでの統計学の黎明

統計学の黎明を要請したものは，社会への不安であった．筆者に言わせれば，この社会への不安を直視したのがドイツ，数で解決しようとしたのがイギリスで，解決への筋道を確率論で基礎づけたのがフランスである．

プロシヤにおける国勢学，イギリスにおける政治算術，フランスにおける古典確率論–統計学はこれら３つの異った厳選を持つと言われる (増山元三郎, 1950, p. 6)．

17世紀初頭から何度も流行を繰り返し，遂に1665年にはロンドンの人口の1/4を死に至らしめた ペストの大流行 は恐怖の対象であった．パンデミックは現代でも恐怖の対象であるが，当時はその全貌の把握が難しく，これが第一に切望された．月の運行による健康被害，国王の統治が疫病を引き起こす，などの俗見が流布していた時代である．しかし，「数」という解決手段は極めて功を奏した．

数による解決が他でもないイギリスから生まれたことは，Francis Bacon 1561-1626 と Thomas Hobbes 1588-1679 に象徴される自然科学の風土，「Aristotelesの三段論法を通じて，経験的に因果関係を発見することで，我々は自然を理解できる」という希望が当時のイギリスには存在したことが挙げられる．

海へ行け，きっと獲物があるぞという先輩が Bacon であった．漁獲法一般の講義をする先生が，例えば後世の J. S. Mill の帰納論理学に相当するのである．統計学を作った漁師たちは，Mill 先生の帰納法の論理学の講義などは，上の空で聞いた．そして各自の漁獲法を自らの浜で覚えたのである． (北川敏男, 1949, p. 12)

新大陸の発見，東洋への海路の開拓により，世界商業の中心は砂漠の商隊と地中海の商人とを介して栄えていたイタリアから，スペイン・ポルトガル・オランダを経て16世紀の終り頃には，すでにイギリスに移っていたのである．ここに興隆の一路を辿る市民社会・殷盛を極める海上貿易・繁栄する英都の商業・封建制の崩壊を示す Cromwell 革命 (1649) 後のイギリス社会に，市民科学としての政治算術が起ったことは敢えて異とするに足りないであろう (増山元三郎, 1950, p. 10)．

1.1.1 John Grauntの死亡表

ペスト流行の激しさの判定に寄与する人口状況を，最初に数によって理解しようとしたのが John Graunt 1620-1674 であった．

当時の英国王立理学協会¹ は，封建的な諸関係の崩壊解消と同時に，商品生産・貨幣による売買の全面支配によって貨幣的表現が富の大部分に侵入したことにより新たに誕生した市民階級が勢力を占めており，Graunt もこのような商人階級の出身であった．

そのような身分の Graunt が英国王の推薦を受けて王立協会員の名誉を勝ち取った論文 (Graunt, 1662) は，ギルド発行の死亡統計 Bills of Mortality と教会に蓄積していた統計資料² から統計的な処理を通じて世界初の「死亡表」を作成し，次の内容を初めて結論づけた．

• 36%の幼児は６歳未満で死亡する．
• 洗礼数をみると，男女比は16:15くらいである．
• 都市の死亡率は地方より高い．
• Londonの城外では死亡率は３倍である．

加えてLondonの世帯数を3通りの方法で推算し，世帯数は5万であろうと結論づけた．なお，当時の俗見ではLondon人口は100万と言われていた．

その後このような「生命表」は精緻化の一途を辿り，イギリスのギルド的な共助制度の土壌の上で，生命保険の成立という実を結んだ．

1.1.2 統計学への期待と希望

このイギリスの数を使った解決は，政治算術学派 と呼ばれ，海外への輸出が進んだ．

ドイツの牧師 Johann Peter Süβmilch 1707-1767 は Graunt に倣って，教会に蓄積していた統計資料を用い，出生率の性別比が長期的には女性1,000対男性1,050に収束することを発見した．

中でも特に，「たくさんのデータを集めると何かが見えてくる」ことに大きな希望を持ち，Graunt が教会の資料に注目したことを Columbus の新大陸発見になぞらえている．そう，歴史上最初の統計分析は，教会の資料によるものであったのである．

若し我々が家を一軒一軒数えていくならば，ある家では娘だけに，またある家では息子だけに，あるいはそうでなくとも，非常に不釣り合いな両者の配合にでくわすであろう．小さな社会や村落でも秩序的なものを認めることは，容易ではない．（中略）．かかる場合に，誰が，能く規則と秩序とに想達し得るだろう．所で，教会の記録はこの秩序の確認のための大きな手段である．それは教会用及び世俗用のためにすでに数世紀前から取られ，とくに宗教改革後はかなり正確にとられてきた．誰がそれを利用したか？その発見はアメリカ発見と同時に可能であったのだ．（中略）それをGrauntがなし得たのである． –Süβmilch (1741) 『神の秩序』 (Göttliche Ordnung) 訳文は (北川敏男, 1949) より．

このように Süβmilch は男児の出生率の方が高いことを神の存在証明と見なしたのであった．この宗教的な外被を取り去るには，確率論の登場をまたねばならなかったが，これにはさらにフランスの学派が合流するのを待つ必要があり，それには100年を要したのであった（ Section 1.7 も参照）．

1.2 ベイズが取り組んだ問題

というわけで，\(i=1,\cdots,n\) 番目の世帯の新生児が，男児である \(y_i=1\) か女児である \(y_i=0\) かのデータなどから，人口・疫病・国家動態に役立つ知識を引き出すことが当時の重要な問題意識であることをわかっていただけただろう．

イギリスの牧師 Thomas Bayes 1701-1761 は，より抽象的な設定で統計的推定の問題を研究していた．Bayes は就中，次のような区間推定の問題を考えていた．

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

ベイズが取り組んだ問題（現代語訳）

2値のデータ \(Y_i\in\{0,1\}\) は，ある未知の「成功率」 \(\theta\in(0,1)\) に従って， \[ Y_i=\begin{cases} 1&\text{確率 }\theta\text{ で}\\ 0&\text{残りの確率} 1-\theta\text{ で} \end{cases} \] という値を取るとする．³ このようなデータの独立観測標本 \(\boldsymbol{y}:=(y_1,\cdots,y_n)^\top\) から．神のみぞ知る，このデータ \(\boldsymbol{y}\) を生み出した真の成功率 \(\theta\) が，区間 \((a,b)\subset(0,1)\) に入っているという確率 \(\operatorname{P}[a<\theta<b|\boldsymbol{y}]\) をどう見積もれば良いか？

ここでは引き続き \(Y_i\) は性別で，\(\theta\) は男児が生まれる確率 \(\theta=\operatorname{P}[Y_i=1]\) だと解釈する．Bayes 自身は「ある未知の位置に白線が引かれたテーブル上にボールを \(n\) 個転がし，それぞれの領域に幾つのボールが入ったかの情報のみから，白線の位置を推定する」という表現によって問題を定式化した (Bayes, 1763)．これは後世ではビリヤード台の問題とも呼ばれた．こちらのサイトも参照．

1.3 ベイズのアイデア

彼の発想は極めてシンプルであり，次の3段階によって推定を試みた：

1. 事前分布 \(p(\theta)\) と呼ばれる，最初の \(\theta\in(0,1)\) に対する予想 \(p(\theta)\) を自由に表現する．⁴
2. 事前分布のデータ \(\boldsymbol{y}\) を観測した下での条件付き分布 \[p(\theta|\boldsymbol{y}):=\frac{p(\theta,\boldsymbol{y})}{p(\boldsymbol{y})}\] を計算する．これを事後分布という．
3. この事後分布 \(p(\theta|\boldsymbol{y})\) の形から区間推定を実行する．

この 3.の部分は，Bayes が特に区間推定に拘ったためのものであり，点推定でも良ければ次期予測でも良い．推定対象 3.を目的に応じて自由に入れ替えても，1.と 2.の部分が同じように動作するということ，これがベイズ統計学の枠組みである．

それだけに事後分布というものが表現力に富んでいるのである．また，以下の例で納得していただけるかもしれないが，ベイズ統計学の手続きは「眼前のデータは，事前の信念を変えるのにどれほど説得的であるか？」という観点からも見れ，定量的であると同時に定性的な判断も可能にする． Section 3.6 で紹介するように，この特徴は意思決定への応用おいても重要である．

問題に対する (Bayes, 1763) の解決

1. まず，事前分布 \(p(\theta)\) を設定する．Bayes は前述のビリヤードの問題を考えていたこともあり， 「\(\theta\in(0,1)\) は全く予想がつかない」「どんな \(\theta\) も同様にあり得る」という立場を取った．横軸を \(\theta\in(0,1)\) の値，縦軸を「主観的にあり得ると思う度合い」として図で表すと次の通りである：

import matplotlib.pyplot as plt
import numpy as np

# Define the range for x-axis
x = np.linspace(0, 1, 1000)

# Uniform distribution density function is constant
y = np.ones_like(x)

# Plot the graph
plt.figure(figsize=(3, 2)) # Size suitable for a smartphone screen
plt.plot(x, y, label='Uniform Distribution (0,1)', color=(0.35, 0.71, 0.73, 1))
plt.fill_between(x, y, color=(0.35, 0.71, 0.73, 0.3))
plt.xlabel('x')
plt.ylim(0, 1.5)
plt.ylabel('Density')
plt.title('Posterior Distribution')
plt.legend()
plt.grid(True)
plt.show()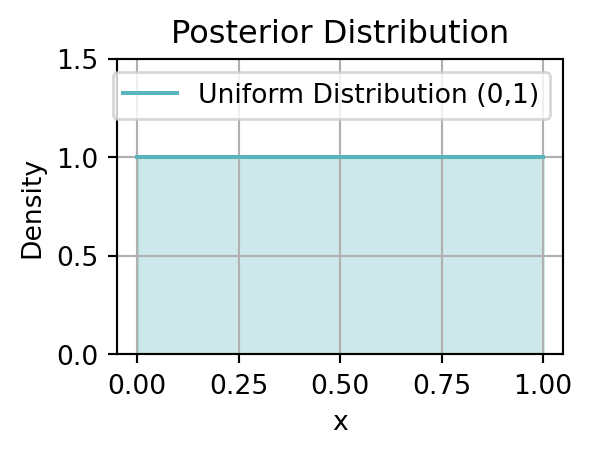

この図が表す \((0,1)\) 上の確率分布を一様分布という．このように，一様分布とは「どのような \(\theta\) の値も同様に確からしい」という予想の表現である．

2. 次に，データ \(\boldsymbol{y}=(y_1,\cdots,y_n)^\top\) が観測された後の条件付き分布 \(p(\theta|\boldsymbol{y})\) を計算することで，本データ \(\boldsymbol{y}\) が事前の信念 \(p(\theta)\) をどのように変えてしまうかを観る．簡単な確率論の結果として，条件付き分布は次の公式によって計算できる（講義ノートも参照）：⁵ \[ p(\theta|\boldsymbol{y})=\frac{p(\boldsymbol{y}|\theta)p(\theta)}{\int_\Theta p(\boldsymbol{y}|\theta)p(\theta)\,d\theta} \tag{1}\]

   例えば 日本の2021年の出生児性別のデータ を用いると次のようになる．

import matplotlib.pyplot as plt
from scipy.stats import beta

# パラメータの設定
n = 811622
male = 415903
female = n - male

# ベータ分布のPDFを計算
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, 1+male, 1+female)

# プロット
plt.figure(figsize=(3, 2))
plt.plot(x, y, label=f'Beta({1+male}, {1+female})', color=(0.35, 0.71, 0.73, 1))
plt.fill_between(x, y, color=(0.35, 0.71, 0.73, 0.3))
plt.xlabel('p')
plt.xlim(0.4, 0.6)
plt.ylabel('Probability Density')
plt.title('Bayesian Posterior Distribution')
plt.legend()
plt.grid()
plt.show()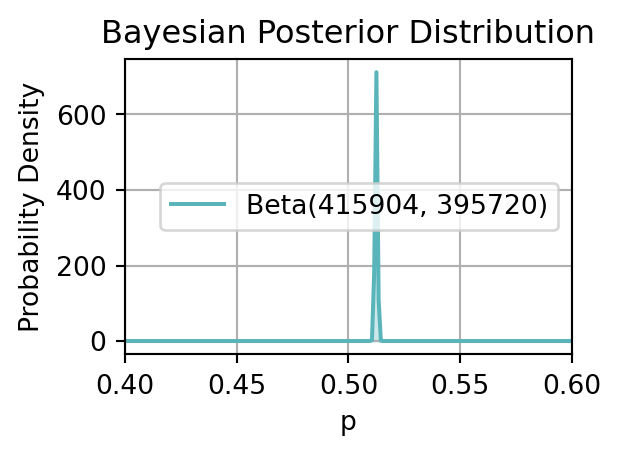

こうして極めて鋭い事後分布が出来た．事前に設定した分布 \(p(\theta)\) は極めて平坦な一様分布であったのに，それをデータで条件付けた \(p(\theta|\boldsymbol{y})\) には極めて鋭いスパイクが現れたのである．式 1 を認めるならば，この図は「男児の方が女児よりも生まれる確率が高い」ことの証拠として，極めて説得的ではないだろうか？

3. では区間推定の例として，\((a,b)=(0.5,1.0)\) として，「男児の方が女児よりも多い確率」を推定しよう．これは次を計算することになる： \[ \begin{align*} &\operatorname{P}\left[\frac{1}{2}<\theta<1\right]\\ &=\int^1_{\frac{1}{2}}p(\boldsymbol{y}|\theta)\,d\theta. \end{align*} \]

print(sum(y[500:600])/1000)

1.0030977682960893

もはや丸め誤差により \(1\) を越してしまっている．ほとんど確実に「男児の方が生まれる確率が高い」と結論づけて良いだろう．

この (Bayes, 1763) が実行したように，事後分布 \(p(\theta|\boldsymbol{y})\) をみて \(\theta\) に関する推論をする，という立場からの統計的営み全体をベイズ統計学．

1.4 ベイズ統計学の基本問題

事後分布 \(p(\theta|\boldsymbol{y})\) を導く際に用いた条件付き確率の公式である 式 1 \[ p(\theta|\boldsymbol{y})=\frac{p(\boldsymbol{y}|\theta)p(\theta)}{\int_\Theta p(\boldsymbol{y}|\theta)p(\theta)\,d\theta}\quad\text{(1)} \] は Bayesの公式 と呼ばれるようになった．今回の場合では，Pythonコードをご覧になった方はわかったかもしれないが，事後分布は \[ p(\theta|\boldsymbol{y})=\frac{\theta^m(1-\theta)^{n-m}}{B(m+1,n-m+1)} \] となり，これはパラメータの空間 \((0,1)\) 上の Beta分布 と呼ばれるものである．

現代のベイズ統計学の多くの統計量は，ある可積分関数 \(g:\Theta\to\mathcal{X}\) を用いて \[ \operatorname{E}[g(\theta)|\boldsymbol{y}]=\int_{\Theta}g(\theta)p(\theta|\boldsymbol{y})\,d\theta \tag{2}\] と表される．先ほどの Bayes の区間推定の例では \(g=1_{(a,b)}\) と取った場合に当たる．⁶ 実は，この積分は，この最も簡単と思われる \(p(\theta),p(\boldsymbol{y}|\theta)\) の設定でも，殆ど計算できないのである．

鮮やかな解決法を提示したかと思えば，結局実行出来ないのでは全く本末転倒である！そのこともあってか，論文 (Bayes, 1763) は実は Bayes の死後に Richard Price によって投稿されたものであり，生前に自ら投稿・発表した訳ではなかった．⁷ 当然，発表当時は全く注目を受けなかった (Stigler, 1990)．

Hence, despite the analytical availability of \(p(\theta|\boldsymbol{y})\) via (2)–“Bayes’ rule” as it is now known-—the quantity that was of interest to Bayes needed to be estimated, or computed. The quest for a computational solution to a Bayesian problem was thus born. (Martin et al., 2023, p. 2)

まとめ：ベイズ統計学の基本問題

ベイズの提示した統一的な統計推測の枠組み

1. 推定したい値 \(\theta\) の空間上に事前分布 \(p(\theta)\) を設定する．
2. 事前分布 \(p(\theta)\) のデータ \(\boldsymbol{y}\) に関する条件付き分布として事後分布 \(p(\theta|\boldsymbol{y})\) を得る．

は非常に自然で，特に確率分布 \(p(\theta),p(\theta|\boldsymbol{y})\) を簡単に視覚化できる現代では「データ \(\boldsymbol{y}\) は，パラメータ \(\theta\) に対する事前の信念をどれほど変えるに値するか？」を定量的にも定性的にも実感出来るという美点がある．

しかしながら，モデル \(p(\theta),p(\boldsymbol{y}|\theta)\) の設定をいくら簡単にしても根本的に計算が困難で実行不可能なのである．これを解決する分野をベイズ計算という．ベイズの論文 (Bayes, 1763) でも，計算法の開発が約半分を占めた．⁸ このように，Bayes統計学は当初からBayes計算の問題を懐胎していたのである．

In short, the implementation of all forms of Bayesian analysis relies heavily on numerical computation. (Martin et al., 2023, p. 2)

1.5 Laplaceの近似

フランスの数学者 Laplace は25歳時の初めての統計に関する著作 (Laplace, 1774) を発表した．この中で，Bayes が解こうとしたものと全く同じ

\[\begin{align*} &\operatorname{P}[a<\theta<b|\boldsymbol{y}]\\ &\quad=\frac{\int^b_a\theta^m(1-\theta)^{n-m}\,d\theta}{B(m+1,n-m+1)} \end{align*} \tag{3}\]

という積分計算の問題を，被積分関数を \[ f(\theta):=\frac{\log p(\theta|\boldsymbol{y})}{n} \] を用いて指数関数の形に表すことで解いた：⁹ \[ \begin{align*} \operatorname{P}[a<\theta<b|\boldsymbol{y}]&=\int^b_ap(\theta|\boldsymbol{y})\,d\theta\\ &=\int^b_ae^{nf(\theta)}\,d\theta \end{align*} \] この形に変形することがどのように役立つかは，次の定理が説明してくれる：

定理（Laplace近似）

¹⁰ 関数 \(f:[a,b]\to\mathbb{R}\) はただ一つの最大値を \(x_0\in(a,b)\) で取り，\(f''(x_0)>0\) を満たすとする．このとき \(n\to\infty\) の極限について， \[ \int^b_ae^{nf(x)}\,dx\sim\sqrt{-\frac{2\pi}{nf''(x_0)}}e^{nf(x_0)} \]

これを \(f\) の二次近似について適用することで，あらゆる確率分布 \(p(\theta|\boldsymbol{y})\,d\theta\) に関する積分 式 3 を，その正規近似に関する積分で近似できるのである．

この手法は現在のBayes計算手法のアイデアの源泉であり続けている (Rue et al., 2009), (MacKay, 2003)．

1.6 ベイズ統計学の長く苦しい時代

「ベイズの枠組みは理念的に好ましかろうと，実際には実行不可能である」というベイズ統計学の基本問題は，Laplace が普遍的な近似計算法を開発したこと（ Section 1.5 ）を除いて，次の進展を見るには計算機の発明と普及を待つ必要があった．その間実に2世紀超えである．

また，Laplace の近似手法は普遍的であり，Bayes の最初の設定のような簡単な設定の \(p(\theta|\boldsymbol{y}),g\) に限らずとも使えるという，ベイズ統計学に大きく資する特徴も備えていたが，パラメータ \(\theta\in(0,1)\) の次元が1ではなくなると途端に使えなくなるという欠点がある．

（前略）ベイズ統計学の有用性は以前から理解されていたが，この問題の抜本的な解決は1980年代まで待たざるを得なかった．それ以前は，ベイズの定理自体は18世紀に早々に発見されたにもかかわらず，長い間，確率の解釈，事前分布の設定，事後分布の計算の困難さのために哲学的議論に終始し，実用化にはほど遠かったのである．実用化の扉の鍵となったのは，一つは計算機の急速な発達，もう一つは計算集約的な画期的アルゴリズムの提案である． (樋口知之, 2014, p. 17)

1.7 フランスでの確率論の歴史

このように，Laplace が，ベイズ統計学暗黒の時代の中で唯一の小さな前進を生んだ．それだけでなく，Laplace は後の1812年に当時の確率論最大の集大成と言える大著『確率論の解析理論』を産んでおり，これが他でもないフランスから生まれたことにも相応の理由があった．

まず第一に，賭博の流行により，確率というものの理解と征服が嘱望された．

その（確率論の）発展の動きを与えたものは，交易を賭ける商業資本家が占星術よりも確実な指導をこの学術に求めるという様な社会が基盤となって存在したことである．例えば，17世紀中葉のPascalとFermatの間の往復文書に取り扱われたカード遊びの数学的問題が，広く人々の関心を呼び起こした事情の裏には，至富の途を確実に求める商人たちの渇望が学問が外の世界にあったことを忘れてはならない． (北川敏男, 1949)

第二に，統計的現象を神学的な畏怖の対象と見るのではなく，自然科学による自然の理解と征服の文脈の最先端として理解する土壌がフランスにあったことが指摘できる．

17, 18世紀の啓蒙的合理主義は，偶然的な事象に対しても数学的な取り扱いを行うことに特別の興味を持った．思想的にはこの時代精神こと確率論を発展させた最大の動力であった．その駆使する数学解析の多彩と合理主義の徹底とに於て，Laplace の大著はよくこの時代を代表するものと言うべきであろう．

当時の財務総監 Jacques Turgot を通じてパリ造幣局の監査官も務めた Nicolas de Condorcet 1743-94 は Laplace の確率論を積極的に社会分析に応用した．「社会数学」と呼んだこの運動は社会学の源流ともみなされる． 当然後進も Laplace に続いた．ベルギーの数学者 Adolphe Quetelet 1796-74 は Laplace の確率論を社会に応用することを目指し「社会物理学」なる分野を創始し，BMIの別名「ケトレー指数」にも名を残している．¹¹

古典確率論の一応の完成は典雅に見えるであろう．だが人は，確率論のもった政治的，社会的意義を忘れてはならない．理知を一切の尺度として「代数学の炉火によって倫理学及び政治学を照さん」(Condorcet) という時代精神，神の啓示に代らんとする確率論，それはフランス革命の思想的基礎に連関することを見失ってはならないのである． (北川敏男, 1949)

1.8 Quetelet による綜合

Quetelet は応用統計学の祖とも呼ばれる．

［政治算術学派から人口理論 (Malthus, 1798) をはじめとする数多くの統計的法則の発見など，多くの成果があったにも拘らず，］18世紀の後半は理論的成果の観点からは全く空白の時代であった．吾々はその原因を方法論が進歩しなかった点に見出しうる．先験的対数法則を中枢とする古典確率論の方法がこれと合流するに至るまで，統計学の理論的分野は足踏みを続けざるを得なかったのである．後述 Quetelet の手による，この合流の着手は，応に近代的意味における統計学の発足を示すものであるとともに，記述統計学の定礎を意味するものでなければならなかった．(増山元三郎, 1950, p. 12)

2 MCMCとSMCの発明

「積分が計算できない」というベイズ統計学の基本問題（ Section 1.4 ）は，計算機の発達と普及も欠かせなかったが，シミュレーションを取り入れた確率的アルゴリズムであるマルコフ連鎖モンテカルロ法 (MCMC) の発明によって本質的に解決された．

しかし，この解決は必ずしも初めからベイズ統計学のために考案されたわけではなく，むしろ物理学と第二次世界大戦とが着火剤となった．アメリカの原爆開発計画において，当時の数値積分法では解けないような高次元の積分を，通常のモンテカルロ積分法は使えない状況下で解く必要があったことが，MCMC発明の契機となった．

In fact, until Bayesians discovered MCMC, the only computational methodology that seemed to offer much chance of making practical Bayesian statistics practical was the portfolio of quadrature methods developed under Adrian Smith’s leadership at Nottingham. (Green et al., 2015, p. 836)

2.1 マルコフ連鎖によるモンテカルロ法の発明

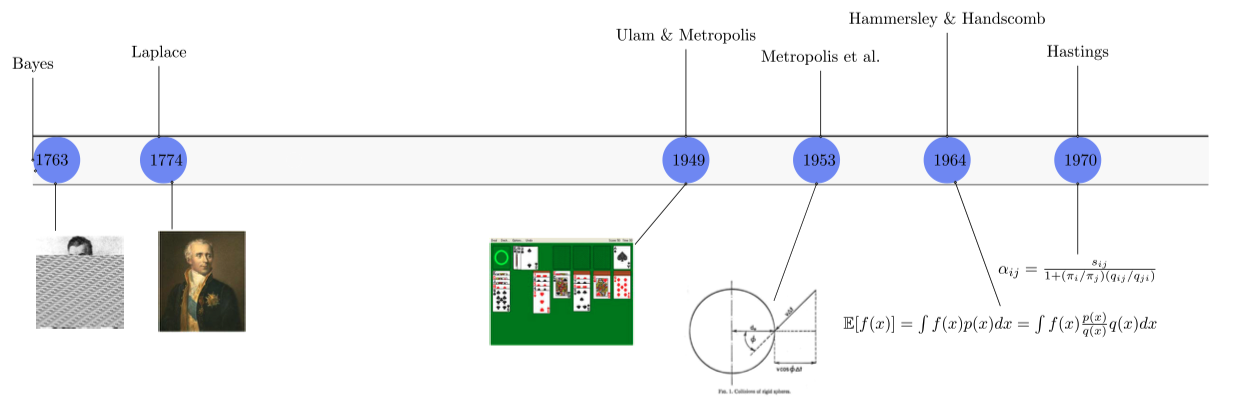
乱数のシミュレーションを用いた確率的なアルゴリズムをモンテカルロ法と総称する．これは Metropolis が同僚 Ulam のポーカー好きから，モナコの首都 Monte Carlo にちなんで名付けたものである (Nicholas Metropolis and Ulam, 1949)．このようなアルゴリズムが最初に生まれたのが，第二次世界大戦中の Los Alamos研究所 で進行中だった原爆開発計画である Manhattan計画 においてである．

当時の問題は，原子爆弾着火時における Schödinger 作用素の基底状態のエネルギーを計算することにあった．抽象的には，\(p\) を \(N\) 個の粒子が従う Boltzmann 分布として，積分 式 2 を計算することにあった：

\[ \operatorname{E}[g(\boldsymbol{\theta})]=\int_\Theta g(\boldsymbol{\theta})p(\boldsymbol{\theta})\,d\boldsymbol{\theta}\quad\text{(2)} \]

ただし，

1. 積分領域 \(\Theta\) が \(2N\) 次元というとてつもない高次元空間上であること
2. 分布 \(p\) は定数倍を除いてしか計算できない

という，2つの大きな制約があった．1.のために通常の数値積分法が使えず，また 2.により \(p\) からの直接の乱数シミュレーションが出来ないので，\(p\) からの乱数 \(X_1,\cdots,X_M\) を十分多く生成することで積分 式 2 を \[ \frac{1}{M}\sum_{i=1}^Mg(X_i) \] によって近似するという通常の Monte Carlo 積分法を実行することも出来ない．そこで，Metropolis ら当時の Los Alamos に集まった物理学者たちは新しい方法を考える必要があった．

最終的な解決 (N. Metropolis et al., 1953) は，Monte Carlo 法の中でもとりわけ画期的な発想によるものであった．それは，Markov 連鎖を用いるということである．Markov連鎖とは（ある一定の条件を満たす）確率過程のクラスであり，\(p\) から直接のシミュレーションが出来ない状況でも，\(p\) に収束するようなMarkov 連鎖を構成することは可能だったのである．

制約 1.と 2.は広く物理学とベイズ統計学の至る所で見られる障壁であり，これをものともしない汎用アルゴリズムの発明は極めて大きなブレイクスルーであった．(Dongarra and Sullivan, 2000) は Metropolis アルゴリズムを理学・工学分野に20世紀最大の影響を与えたアルゴリズムの1つとしている．

2.2 重点サンプリング法の発明

実は Manhattan 計画に最中に，もう一つのサンプリング技法が生まれていた．厚い壁で中性子線とガンマ線がどのように吸収されるかに取り組んでいたグループにて，Herman Kahn らが中心となり，式 2 の分布 \(p\) に関する積分が \[ \begin{align*} \operatorname{E}[g(\boldsymbol{\theta})]&=\int_\Theta g(\boldsymbol{\theta})p(\boldsymbol{\theta})\,d\boldsymbol{\theta}\\ &=\int_\Theta\frac{g(\boldsymbol{\theta})p(\boldsymbol{\theta})}{p^*(\boldsymbol{\theta})}p^*(\boldsymbol{\theta})\,d\boldsymbol{\theta} \end{align*} \] という式変形により，別の分布 \(p^*\) からのサンプリングを通じて計算できる，という技法が利用された．彼らはこれに重点サンプリング法という名前をつけた．これは Gerald Goertzel による命名である可能性が高い (Andral, 2022)．

なお，当時は \(p\) からのサンプリングを回避できるという点よりも，\(p^*\) をうまく選ぶことにより元々の \(p\) を用いた Monte Carlo 積分法を適用するよりも近似の精度をあげることが出来るという点の方が注目された (Hammersley and Handscomb, 1964)．

前節の Metropolis 法がMCMCの先駆けであるとしたら，この2つの美点を持った重点サンプリング法は，SMC（粒子フィルター） の先駆けであった．

2.3 MCMCの普及とギブスサンプラー

Metropolis 法の発明から，すぐにMCMCの画期性が広く認識された訳ではなかった．特に，元々物理学の文脈で発明されたこともあり，統計学の文脈への応用が始まるには (Hastings, 1970) の仕事を待つ必要があった．

しかし1970年代とはマイクロプロセッサが開発されたばかりの時代であり，¹² MCMCが実際の統計解析の現場で採用可能な計算手法になるとは（そもそも現代のように小型なコンピュータを個人が所有するようになるとは）夢にも思われなかった時代であったが，ここからたったの20年で現代人の生活とベイズ統計学は大きく変わることになる．

1. 各人が安価に高性能なコンピュータを所有するようになった．
2. 高次元分布からのサンプリングを可能にするアルゴリズムが発見された．

の2点が最後に加わることで，MCMCがベイズ計算法不動の金科玉条となった．

この 2.は計算機の性能の問題だけでなく，統計的画像処理 の分野から Gibbsサンプラー という新たなアルゴリズムが生まれた (Geman and Geman, 1984) ことによって実現された．¹³ これは，パラメータが \(\boldsymbol{\theta}=(\theta_1,\theta_2)^\top\) と表されるとき，適切に定めた初期値 \(\theta_2^{(0)}\) から初めて，条件付き分布からのサンプリング \[ \theta_1^{(i)}\sim p_1(\theta_1^{(i)}|\theta_2^{(i-1)},\boldsymbol{y}), \] \[ \theta_2^{(i)}\sim p_2(\theta_2^{(i)}|\theta_1^{(i)},\boldsymbol{y}), \] を繰り返すことで，最終的に \(\boldsymbol{\theta}^{(i)}:=(\theta_1^{(i)},\theta_2^{(i)})^\top\) は全体として \(p(\boldsymbol{\theta}|\boldsymbol{y})\) に従うように収束する，という技法である．

Gibbs 法により，パラメータ \(\boldsymbol{\theta}\) の次元が大きく，直接のサンプリングが難しい場合や，条件付き分布の系はわかっているが結合分布がわからない場合¹⁴ でも，\(\boldsymbol{\theta}=(\theta_1,\theta_2,\cdots)\) というように低次元変数の結合と理解することで，あるいは補助変数を追加してわざと問題を高次元化してでもそのような状況をうまく作り出すことで (Tanner and Wong, 1987) ，部分的な低次元サンプリングから組み上げることが出来るようになった．これを データ拡張 ともいう．さらにその後も，このアイデアが (Roberts and Rosenthal, 1999) のスライスサンプラーにつながっている．

この点をはっきり強調して示し，ベイズ統計学がすでに実行可能なものになっており，ベイズ統計学の基本問題（ Section 1.4 ）もすでに過去の遺物となっているということを，統計学界隈に広く知らしめたのが (Gelfand and Smith, 1990) であった．

3 ベイズ統計学のこれから

複雑化の一途を辿るモデル・データに対応できるベイズ計算手法の開発が，今後最も重要な課題である．情報コミュニケーション技術が高度に発展した現代ならではの課題は，次の3つに大きく分類できる：

1. 尤度不明モデル：尤度が解析的に得られない（または計算不可能）ほどに複雑なモデル
2. 変数 \(\boldsymbol{\theta}\) が高次元である：多くの変数を考慮に入れた高次元モデル
3. 観測 \(\boldsymbol{y}\) が高次元である：ビッグデータを用いた解析

3.1 擬似周辺尤度法

実は尤度 \(p(\boldsymbol{y}|\boldsymbol{\theta})\) が解析的に得られない場合や計算が極めて困難になる場合でも，この不偏推定量があればMCMCを実行して事後分布を得るのに十分である (Andrieu and Roberts, 2009)．この尤度 \(p(\boldsymbol{y}|\boldsymbol{\theta})\) の不偏推定量を得るのに粒子フィルターを用いた場合を，特に粒子MCMCという (Andrieu et al., 2010)．

このときの不偏推定量の性能が最終的な Monte Carlo 推定量に影響する．不偏推定量の分散を改善するには，サブルーチンである粒子フィルターの反復数を増やす必要がある．すると本体であるMCMCの反復数とのトレードオフが生じる．こうしてアルゴリズムの最適な調整が課題になる．

3.2 高次元問題に対処するMCMC

ほとんどのMCMC手法は，データサイズやモデルのパラメータサイズの増加に対して，計算負荷が飛躍的に上昇する次元の呪いに苦しむ．これを克服する手法はscalabilityの名の下に盛んに研究されている (鎌谷研吾, 2021, p. 394)．

1. 対象分布の探索を効率よく行う手法として，HMC (Hamiltonian Monte Carlo) 法が提案された (Neal, 2011)．他にも NUTS (No U-Turn Sampling) (Hoffman and Gelman, 2014), Metropolis-Adjusted Langevin Algorithm (Roberts and Tweedie, 1996), Stochastic Gradient MCMC (Nemeth and Fearnhead, 2021), PDMP (区分的確定なMCMC) (Bierkens et al., 2018), (Fearnhead et al., 2018) とジグザグサンプラーなどがある，
2. より良い提案分布の選択法について，MH法の最適スケーリング法，適応的サンプリング，焼き戻しなどの手法がある．
3. 並列計算による効率化の方向性には，並列MCMC，完全サンプリングなどの手法がある．
4. 他の分散低減法に，Rao-Blackwell化 (Casella and Robert, 1996)，操作変数法などがある．

ジグザグサンプラーについては，以下の記事も参照：

新時代の MCMC を迎えるために

モンテカルロ法の発展とは，背後の物理現象からの離陸の歴史でした．非対称な Metropolis-Hastings アルゴリズムがどのように生まれたかと，その最先端のアイデアと言える連続時間 MCMC 法の歴史を，サンプルコード付きで紹介します．（2024 年度統計数理研究所オープンハウス）

3.3 近似ベイズ手法

上述までの手法はいずれもシミュレーションを十分多く行えば（理論的には）任意の精度で正しい値を得ることができるが，¹⁵ その適用範囲やスケーラビリティが課題なのであった．そこで同時に，最初からある許容精度を定めた下での近似を実行することとし，代わりにより広い適用可能性と計算速度を得るための手法も探求されている．これを近似ベイズ法という．

一つのアプローチはシミュレーションによる方法である．これにはABC (Approximation Bayesian Computation) (Tavaré et al., 1997) と BSL (Bayesian synthetic likelihood) (Price et al., 2018) の2つの手法があるが，いずれもデータ生成過程（モデル）の複雑性と高次元性という２つの障壁が併存したときでも使える手法である．ABCではまず事後分布 \(p(\boldsymbol{\theta}|\boldsymbol{y})\) をある低次元な要約統計量 \(S:\mathcal{Y}\to\mathbb{R}^d\) を用いて \(p(\boldsymbol{\theta}|S(\boldsymbol{y}))\) で近似し，さらに尤度 \(p(\boldsymbol{y}|\boldsymbol{\theta})\) を直接評価することは回避し，シミュレーションのみを用いて \(p(\boldsymbol{\theta}|S(\boldsymbol{y}))\) を推定する．BSLはさらに尤度 \(p(S(\boldsymbol{y})|\boldsymbol{\theta})\) にパラメトリックな仮定をおく．

第二に最適化による方法がある．変分ベイズ手法とは，これは大きなパラメトリックモデル \(\{q^*(\boldsymbol{\theta})\}\) の中から \(p(\boldsymbol{\theta}|\boldsymbol{y})\) に最も近いものを選ぶ手法である．一方で INLA (integrated nested Laplace approximation) とは，Laplaceの近似（ Section 1.5 ）に最適化を組み合わせて高次元の問題にも対応する．

ABCでは逐次モンテカルロ法も大きな役割を果たしており，ABC-SMC (Sisson et al., 2007)，ABCフィルタリング (Jasra et al., 2012)，更には変分Bayes法への応用 (Tran et al., 2017) なども進んでいる．

変分Bayesの枠組みでは，モデルの誤想定に頑健な手法の開発も試みられている (Wang and Blei, 2019)．

3.4 ベイズ統計モデリングが理論モデルの実証に役立つ

ベイズモデリングの有用性は，（上述のベイズ計算の問題を除けば）どんなに複雑で大規模なモデルでも，統一的な思想と方法で対応できる点にある．

メカニズムを明示的に表現した数理社会学の数理モデルを，論理的に飛躍することなくダイレクトに統計モデルへと接続できるベイズ統計モデリングは，理論モデルベースの実証研究と相性のよい，たいへん便利な方法と言えるだろう． (浜田宏, 2022, p. 137)

MCMCの開発とパッケージへの実装，そして安価で高性能な計算機が普及してからというもの，ベイズ統計学の興隆は目覚ましく，現在ではベイズ統計学は統計学に関する論文の1割強を占め，諸科学分野全体に浸透しつつある．経済学・心理学への応用は早かったのに比べて，政治科学・社会科学への応用は遅れ気味であり，社会学での使用はまだ稀であると言える (Lynch and Bartlett, 2019)．

3.5 ベイズによる逆問題

ベイズ統計学の枠組みは，逆問題の文脈においても有用である．逆問題とは，観測データ \(\boldsymbol{y}\) が与えられたときに，そのデータを説明するようなモデルのパラメータ \(\boldsymbol{\theta}\) を推定する問題である．

3.6 ベイズによる因果推論

前節に挙げたベイズモデリングの美点は因果推論の文脈でも全く同様である．特に因果推論の問題では推定対象が複雑であることが多いが，このような場合でも全く同じ枠組みを提供してくれるのがベイズである．頻度論的接近では設定に応じた個別具体的な議論がベイズ計算の問題に帰着する点が利点として働くことは多いようである (Li et al., 2023)．

実際，ベイズノンパラメトリック手法は2016年の大西洋因果推論カンファレンスのコンペティションで大きな成功を見ている (Dorie et al., 2019)．加えて強い理論的な保証も得られつつあり (Ray and van der Vaart, 2020)，これにより因果推論分野で大きな注目を集めている (Linero and Antonelli, 2023), (Daniels et al., 2023)．

加えて，「あらゆる種の不確実性に対する統一的な定量化を与える」というベイズの性質は，因果推論から意思決定までの接続を地続きにし，例えば属人化医療などの現場でのダイナミックな意思決定に活用できることが期待される．

不確実性を定量化するのに、ベイズ計算では必ず『確率』を使います。一般の人から見たら、統計で確率を使うのは当たり前と思うでしょうが、じつは他の統計手法ではそうでもなく、さまざまな解釈が生まれてしまう。定量化にはすべて統一的に確率を使うベイズ計算は、非常にシンプルなので、最終的にすべての統計はベイズに行き着くしかないと思っています．鎌谷研吾

しかし，ベイズの方法が因果推論の分野で普及するための障壁は，近づきやすさにあると議論できる (Li et al., 2023)．従来の頻度論的な因果推論手法の成功には，潜在反応モデルの特定を殆どしなくて良いこと（モデルフリー），実装が簡単であることが少なからず寄与しているとすれば，ベイズ的接近もこれに当たるものを提供できるようになる必要があるだろう．Stan言語 (Carpenter et al., 2017) はこの方向への大きな試みである．

3.7 ベイズ学習

機械学習の手法を用いてベイズ推論を実行する営みをベイズ学習，または単に「機械学習への確率論的アプローチ」と言ってベイズの枠組みを暗に指す場合も多い (Murphy, 2022), (Ghahramani, 2013)．

古典的な統計手法と同様，多くの既存の（頻度論的）手法にはベイズ手法の対応物が存在する．ベイズの方法だと推定の確信度合いもセットで定量化され，頻度論的対応物よりも得られる情報が多い一方で，計算は既存手法よりも難しいことが多いという構造は，機械学習においても変わらない．

実際，現存のニューラルネットワークの訓練法を超えるベイズ計算法が今後提案されるとは考えにくいが，その最適化する所の目的関数が例えば正則化項付きの平均自乗誤差である場合は，ある正規事前分布と正規尤度に対するMAP推定量に対応する (Seitz 2022)．畢竟，多くの既存手法も「ベイズ学習を非ベイズ的な方法で実行している」と捉えられるのである（逆も然り）．

中でもベイズ学習を採用するのが良い場面としては，モデルの大きさに対して学習に使えるデータの数が少ない場合や，モデルに事前情報を組み込みたい場合¹⁶ ，さらには医療・政策への応用など意思決定に繋げるために不確実性の定量化が肝要な場面などがあり得る．

実際，ベイジアン・ニューラルネットワークでは計算の困難ささえ乗り越えれば，複数の適切なモデルに対し，事後分布によって平均を取って最終的なモデルとすることで，過学習を防止し (Mackay, 1995)，大きな性能改善を得ることができる (Wilson and Izmailov, 2020)．¹⁷

3.8 21世紀の統計学とベイズの役割

このように，21世紀に入ってからベイズの成功は目まぐるしく，この傾向はさらに進むと思われる．これは統計計算の手法の進化によって達成された．今後とも統計計算の手法は，シミュレーション・変分法・最適化の垣根を超えて多様化の一途を辿るだろう (Green et al., 2015, p. 857)．

その中でも筆者は，ベイズ手法が提供する事後分布として得られる不確実性の表現・視覚化が，計算機・自然・人間の間のよきインターフェイスとなっていくことを願っている．¹⁸

The applied statistician should be Bayesian in principle and calibrated to the real world in practice-—appropriate frequency calculations help to define such a tie. (Rubin, 1984)

References

Andral, C. (2022). An attempt to trace the birth of importance sampling.

Andrieu, C., Doucet, A., and Holenstein, R. (2010). Particle markov chain monte carlo methods. Journal of the Royal Statistical Society Series B: Statistical Methodology, 72(3), 269–342.

Andrieu, C., and Roberts, G. O. (2009). The pseudo-marginal approach for efficient monte carlo computations. The Annals of Statistics, 37(2), 697–725.

Bayes, T. (1763). An essay towards solving a problem in the doctrine of chances. By the late rev. Mr. Bayes, f. R. S. Communicated by mr. Price, in a letter to john canton, a. M. F. R. s. Philosophical Transactions, 53(1763), 370–418.

Bierkens, J., Bouchard-Côté, A., Doucet, A., Duncan, A. B., Fearnhead, P., Lienart, T., … Vollmer, S. J. (2018). Piecewise deterministic markov processes for scalable monte carlo on restricted domains. Statistics & Probability Letters, 136, 148–154.

Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., … Riddell, A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1), 1–32.

Casella, G., and Robert, C. P. (1996). Rao-blackwellisation of sampling schemes. Biometrika, 83(1), 81–94.

Daniels, M. J., Linero, A., and Roy, J. (2023). Bayesian nonparametrics for causal inference and missing data. Chapman; Hall/CRC.

Dongarra, J., and Sullivan, F. (2000). Guest editors introduction to the top 10 algorithms. Computing in Science & Engineering, 2, 22–23.

Dorie, V., Hill, J., Shalit, U., Scott, M., and Cervone, D. (2019). Automated versus do-it-yourself methods for causal inference: Lessons learned from a data analysis competition. Statistical Science, 34(1), 43–68.

Fearnhead, P., Bierkens, J., Pollock, M., and Roberts, G. O. (2018). Piecewise deterministic markov processes for continuous-time monte carlo. Statistical Science, 33(3), 386–412.

Gelfand, A. E., and Smith, A. F. M. (1990). Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association, 85(410), 398–409.

Geman, S., and Geman, D. (1984). Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6(6), 721–741.

Ghahramani, Z. (2013). Bayesian non-parametrics and the probabilistic approach to modelling. Philosophical Transactions of the Royal Society A: Mathematical Physical and Engineering Sciences, 371.

Graunt, J. (1662). Natural and political observations mentioned in following index, and made upon the bills of mortality.

Green, P. J., Łatuszyński, K., Pereyra, M., and Robert, C. P. (2015). Bayesian computation: A summary of the current state, and samples backwards and forwards. Statistics and Computing, 25(4), 835–862.

Hammersley, J. M., and Handscomb, D. C. (1964). Monte carlo methods. Springer Dordrecht.

Hastings, W. K. (1970). Monte carlo sampling methods using markov chains and their applications. Biometrika, 57(1), 97–109.

Hoffman, M. D., and Gelman, A. (2014). The no-u-turn sampler: Adaptively setting path lengths in hamiltonian monte carlo. Journal of Machine Learning Research, 15, 1593–1623.

Jasra, A., Singh, S. S., Martin, J. S., and McCoy, E. (2012). Filtergin via approximate bayesian computation. Statistics and Computing, 22, 1223–1237.

Laplace, P. S. (1774). Mémoire sur la probabilité des causes par les évènemens. Mémoires de Mathématique Et de Physique Presentés à l’Académie Royale Des Sciences, Par Divers Savans, & Lûs Dans Ses Assemblées, 6, 621–656.

Li, F., Ding, P., and Mealli, F. (2023). Bayesian causal inference: A critical review. Philosophical Transactions of the Royal Society A: Mathematical Physical and Engineering Sciences, 381(2247).

Linero, A. R., and Antonelli, J. L. (2023). The how and why of bayesian nonparametric causal inference. WIREs Computational Statistics, 15(1), e1583.

Lynch, S. M., and Bartlett, B. (2019). Bayesian statistics in sociology: Past, present, and future. Annual Review of Sociology, 45, 47–68.

Mackay, D. J. C. (1995). Probable networks and plausible predictions —a review of practical bayesian methods for supervised neural networks. Network: Computation in Neural Systems, 6(3), 469–505.

MacKay, D. J. C. (2003). Information theory, inference and learning algorithms. Cambridge University Press.

Malthus, T. R. (1798). An essay on the principle of population, as it affects the future improvement of society, with remarks on the speculations of mr. Godwin, m. Condorcet and other writers. J. Johnson, London.

Martin, G. M., Fraizier, D. T., and Robert, C. P. (2023). Computing bayes: From then ‘til now. Statistical Science, Advanced Publication, 1–17.

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E. (1953). Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6), 1087–1092.

Metropolis, Nicholas, and Ulam, S. M. (1949). The monte carlo method. Journal of the American Statistical Association, 44(247), 335–341.

Murphy, K. P. (2022). Probabilistic machine learning: An introduction. MIT Press.

Neal, R. M. (2011). In S. Brooks, A. Gelman, G. Jones, and X.-L. Meng, editors, pages 113–162. Chapman; Hall/CRC.

Nemeth, C., and Fearnhead, P. (2021). Stochastic gradient markov chain monte carlo. Journal of the American Statistical Association, 116(533), 433–450.

Pearson, K. (1926). Letters to editor. Nature, 117(2946), 551–552.

Price, L. F., Drovandi, C. C., Lee, A., and Nott, D. J. (2018). Bayesian synthetic likelihood. Journal of Computational and Graphical Statistics, 27(1), 1–11.

Ray, K., and van der Vaart, A. (2020). Semiparametric bayesian causal inference. The Annals of Statistics, 48(5), 2999–3020.

Roberts, G. O., and Rosenthal, J. S. (1999). Convergence of slice sampler markov chains. Journal of the Royal Statistical Society Series B: Statistical Methodology, 61(3).

Roberts, G. O., and Tweedie, R. L. (1996). Exponential convergence of langevin distributions and their discrete approximations. Bernoulli, 2(4), 341–363.

Rubin, D. B. (1984). Bayesianly justifiable and relevant frequency calculations for the applied statistician. The Annals of Statistics, 12(4), 1151–1172.

Rue, H., Martino, S., and Chopin, N. (2009). Approximate bayesian inference for latent gaussian models by using integrated nested laplace approximations. Journal of the Royal Statistical Society Series B: Statistical Methodology, 71(2), 319–392.

Sisson, S. A., Fan, Y., and Tanaka, M. M. (2007). Sequential monte carlo without likelihood. PNAS (Proceedings of the National Academy of Sciences of the United States of America), 104(6), 1760–1765.

Stigler, S. M. (1990). The history of statistics: The measurement of uncertainty before 1990. Harvard University Press.

Sun, S., Zhang, G., Shi, J., and Grosse, R. (2019). Functional variational bayesian neural networks. In International conference on learning representations.

Tanner, M. A., and Wong, W. H. (1987). The calculation of posterior distributions by data augmentation. Journal of the American Statistical Association, 82(398).

Tavaré, S., Balding, D. J., Griffiths, R. C., and Donnelly, P. (1997). Inferring coalescence times from DNA sequence data. Genetics, 145(2), 505–518.

Tran, M.-N., Nott, D. J., and Kohn, R. (2017). Variational bayes with intractable likelihood. Journal of Computational and Graphical Statistics, 26(4), 873–882.

Wang, Y., and Blei, D. M. (2019). Variational bayes under model misspecification. Proceedings of the 33rd International Conference on Neural Information Processing Systems, (1198), 13379–13389.

Wilson, A. G., and Izmailov, P. (2020). Bayesian deep learning and a probabilistic perspective of generalization. In Proceedings of the 34th international conference on neural information processing systems. Red Hook, NY, USA: Curran Associates Inc.

北川敏男. (1949). 統計学の認識. 白揚社.

増山元三郎. (1950). 推計学への道. 東大協組出版部.

安藤洋美. (1995). 最小二乗法の歴史. 現代数学社.

樋口知之. (2014). 統計数理の誕生とその広がり. 横幹, 8(1), 14–21.

浜田宏. (2022). ベイズで広がる数理社会学の世界. 理論と方法, 37(1), 124–137.

鎌谷研吾. (2021). マルコフ連鎖モンテカルロ法における平均回帰. 日本統計学会誌, 50(2), 381–402.

Footnotes

1. 正式名称をThe Royal Society for the Improvement of Natural Knowledge by Experimentという

2. 当局の人間に死亡を報告する義務は全くなかった。その代わり、それぞれの教区では2人かそれ以上の死体を調査し、死因を決定する義務を負う調査員を任命していた。「調査員」は死亡を報告する毎に遺族より少額の手数料を徴収する資格が与えられていたので、教区では任命しなければ貧困のため救貧税による支援が必要となりそうな人間を割り当てていた。（Wikipediaページより）

3. これは統計的モデルとしてBernoulli分布 \(Y_i|\theta\overset{\text{iid}}{\sim}\mathrm{Ber}(\theta)\) を仮定するということである．

4. パラメータ \(\theta\) は「男児が生まれる確率」であるが，これ自体にも事前分布という「確率」\(p(\theta)\) を導入することに戸惑う読者も居るだろう．しかし，これがベイズ統計学の特徴である．「男児が生まれる確率 \(\theta\)」だろうとなんだろうと，「わからない」「不確実性がある」と主観的に感じるあらゆる対象に，確率分布を導入して事後分布を得ることで推論を実行する，これがベイズ統計学の枠組みの普遍性であり，無差別性であり，有用性を支えている．

5. 各 \(\theta\) の下で目の前のデータ \(y_1,\cdots,y_n\) が生成される確率 \(p(\boldsymbol{y}|\theta)\) が低いということは，「その \(\theta\) から生成されたデータである確率は低い」という逆の発想ができる．そこで \(p(\boldsymbol{y}|\theta)\) という条件付き確率を尤度ともいう．今回は \(p(\boldsymbol{y}|\theta)=\theta^{\sum_{i=1}^ny_i}(1-\theta)^{\sum_{i=1}^n(1-y_i)}\) である．

6. さらに，\(g(\theta)=\theta^p\) と取った場合，事後積率という統計量になる．等に \(p=1\) の場合が事後平均である．

7. なお，1763に出版されたものはPriceによる補遺も付いた短縮版であり，全文は1974年に出版された．(Stigler, 1990)

8. pp.376-403 がBayesの論文の本論の内容であり pp.399-403 で計算法を３つのルールにまとめているが，その導出部は一部「長すぎるから掲載を省略する」とされている．

9. 一方で，Bayesの逆確率の問題への言及自体は，Laplaceの後年の1781年の著作Mémoire sur les probabilitésへのCondorcetによる序文で初めて登場する (Martin et al., 2023, p. 5)．

10. nCatLab 参照．

11. (安藤洋美, 1995) も参照．

12. 1970年にインテルが世界初の DRAMである Intel 1103 を発売した．Wikipediaページ参照．

13. 物理学では Heat Bath 法と呼ばれ古くから同様のアルゴリズムが存在したが，統計学界隈では現在でも Gibbs サンプラーと呼ばれる．

14. 統計的画像処理など，Markov 確率場 によってモデリングされる対象においてはよくある状況である．

15. この性質を指して，approximateの対義語としてexactという形容詞で表現される．

16. functional Bayes (Sun et al., 2019) という手法では，希望する入力と出力の組を事前に用意するのみで，適切な事前分布を提案してくれる枠組みである．

17. (Wilson and Izmailov, 2020) によると，二重降下現象も見られない．

18. 推定結果に自信がないときはそう表明してくれる機械は親しみやすい．