フローベース模型による条件付き生成

概要

拡散模型は拡張性にも優れており，条件付けが容易である．現状は誘導付き拡散によってこれが実現されるが，連続的な条件付き生成のために，フローマッチングなる方法も提案された．

1 誘導

拡散模型の美点には，条件付けが可能で拡張性に優れているという点もある．

実際，拡散模型の出現後，Conditional VAE (Kingma et al., 2014) などの従来手法を凌駕する条件付き生成が可能であることが直ちに理解された．

\(C\) がクラスラベルなどの離散変数である場合，「誘導」による条件付き生成が初めに考えられた．

1.1 はじめに

「誘導」ではまず，DDPM (Ho et al., 2020) でタイムステップ \(t\) を positional encoding したようにして，プロンプト \(c\) をデータに埋め込む．¹

そしてデータ \(X\) とそのラベル \(C\) に対して，条件付き分布 \(\mathcal{L}[X|C]\) をモデリングする．

しかしこのアプローチの問題は，ラベル \(C\) が不確実な場合などは，この情報を無視して普通の \(X\) が生成されてしまいがちであることである．

そこで目的関数に，条件付き分布 \(X|C\) の正確性を期すような追加のデザインをする．これが「誘導」である．

1.2 条件付きスコア場

条件付き分布 \(p(x|c)\) を学習することを考える．

このとき \(p(x|c)\) のスコアは，Bayes の定理から次のように表せる： \[ \log p(x|c)=\log p(c|x)+\log p(x)-\log p(c), \] \[ \therefore\qquad\nabla_x\log p(x|c)=\nabla_x\log p(x)+\nabla_x\log p(c|x). \tag{1}\]

すなわち，条件付き確率 \(p(x|c)\) のスコア場は，条件なしのスコア場 \(\nabla_x\log p(x)\) と，分類器のスコア場 \(\nabla_x\log p(c|x)\) の重ね合わせになる．

1.3 分類器による誘導 (CG)

式 (1) から，\(\nabla_x\log p(x|c)\) が計算できる分類器 \(p(c|x)\) を新たに訓練すれば，既存のモデル \(\nabla_x\log p(x)\) から，サンプリング方法を変えるだけで条件付き生成ができる．

これを CG: Classifier Guidance (Dhariwal and Nichol, 2021) といい，サンプリング中に各ステップで少しずつ \(x_t\) が \(p(x_t|c)\) に近づくように「誘導」されていく．

さらに，\(c\) が無視されがちな場合も見越して，誘導スケール (guidance scale) という新たなハイパーパラメータ \(\lambda\ge0\) を導入し，次のスコア \[ \nabla_x\log p(x)+\lambda\nabla_x\log p(c|x). \tag{2}\] からサンプリングすることも考えられる．

\(\lambda>1\) としどんどん大きくしていくと，クラスラベル \(c\) に「典型的な」サンプルが生成される傾向にある．

1.4 分類器なしの誘導

CG はいわばアドホックな方法であり，外部の分類器 \(p(c|x)\) に頼らない方法を考えたい．

そのためには，式 (2) から \(p(c|x)\) を消去して \[ \lambda\nabla_x\log p(x|c)+(1-\lambda)\nabla_x\log p(x) \tag{3}\] とみて，\(p(x|c),p(x)\) のいずれもデータから学ぶ．

このアプローチを Classifier-Free Diffusion Guidance (Ho and Salimans, 2021) という．

その際は，新たなクラスラベル \(\emptyset\) を導入して \[ p(x)=p(x|\emptyset) \] とみなすことで，\(p(x|c),p(x)\) を同一のスコアネットワークでモデリングする．

データセット内にランダムに1から2割の画像をクラスラベル \(\emptyset\) と設定することで，これを実現する．

同様の方法を，スコアマッチングではなくフローマッチングを行うことを (Dao et al., 2023), (Q. Zheng et al., 2023) が提案している．

この方法は，追加の分類器の訓練が必要ないだけでなく，サンプリングのクオリティも向上する (Nichol et al., 2022), (Saharia, Chan, Chang, et al., 2022)．これは分類タスクで訓練されたスコア \(\log p(c|x)\) はどう訓練してもスコアネットワークで学習したスコア (3) に匹敵する「良い」勾配が得られないためである．

1.5 高解像度画像生成への応用

1.5.1 Cascaded Generation

条件付き生成の技術はそのままで，最終的なクオリティを向上させるためには，Cascading (Ho et al., 2022) が使用可能である．

これは，画像生成は \(x\) の解像度が低い状態で行い，この低解像度画像を次の条件付き拡散モデルの条件付け \(c\) として，条件付き生成を 高解像度化 (super-resolution) に用いるものである (Saharia et al., 2023)．

この方法の美点は，条件付き生成器をたくさんスタックしたのちに，拡散模型間の段階でも Gauss ノイズや blur を印加することで，さらに最終的なクオリティが上げられるという (Ho et al., 2022)．これを conditioning augmentation と呼んでいる．

この方法は最初から高解像度での生成を目指して大規模な単一の拡散模型を設計するよりも大きく計算コストを削減できる．

Google も Imagen (Saharia, Chan, Saxena, et al., 2022) でこのアーキテクチャを用いている．

1.5.2 Self-Conditioning (T. Chen et al., 2023)

拡散モデルを自己再帰的に用い，自身の前回の出力を今回の入力として逐次的にサンプリングを繰り返すことで，サンプリングのクオリティをさらに向上する自己条件づけが (T. Chen et al., 2023) で提案された．

この方法は RoseTTAFold Diffusion (Watson et al., 2023) によるたんぱく質構造生成でも用いられている：

RFdiffusion generating a novel protein that binds to the insulin receptor. Taken from Baker Lab HP

1.6 逆問題への応用

一方で単一の \(Y=y\) を想定した状況では，非償却的な方法を採用することでさらに精度を上げることが考えられる．

\(\log p_t(x_t|y)\) を一緒くたに \(s^\theta_{t}(x_t,y)\) に取り替えてしまうのではなく，まず第一項 \(\nabla_x\log p_t(x_t|y)\) を \(s_t^\theta(x_t)\) により統一的にモデリングする．

そして \(\nabla_x\log p_t(y|x_t)\) の項は Tweedie の推定量 \[ \widehat{x}_0:=\operatorname{E}[x_0|x_t]=\frac{1}{\sqrt{\overline{\alpha}_t}}\biggr(x_t+(1-\overline{\alpha}_t)\nabla_{x_t}\log p_t(x_t)\biggl) \tag{4}\] を通じて \[ p(y|x_t)\approx p(y|\widehat{x}_0) \] によって近似する．式 (4) の \(\nabla_{x_t}\log p_t(x_t)\) に事前に訓練したスコアネットワーク \(s_t^\theta(x_t)\) を用いる．

(Chung et al., 2023) はこの方法を Computer Vision における非線型逆問題に適用している．

(Song et al., 2023) では Monte Carlo 法が用いられている．

拡散模型の一般の事後分布サンプリングのための応用については次稿も参照：

拡散モデルによる事後分布サンプリング

Langevin 拡散の時間反転を用いたシミュレーションベースのサンプリング法

2024-08-03

2 フローマッチングによる連続な条件付け

2.1 連続な条件付き生成

連続な変数に対する条件付き確率からの生成は CcGAN (Ding et al., 2021) などでも試みられていた．

AlphaFold 3 (Abramson et al., 2024) や RoseTTAFold Diffusion (Watson et al., 2023), (Krishna et al., 2024) など，たんぱく質構造生成模型において拡散モデルが用いられている理由も，高精度な条件付き生成が可能であることが大きいという．

このことに加えて連続な変数に対する条件付けを可能にすることは，拡散モデルの拡張性をさらに高めることになる．

そもそも拡散モデルは連続時間正規化流 (CNF) と合流し，フローマッチング（第 2.2 節）によりノイズ分布 \(P_0\) をデータ分布 \(P_1\) に変換する曲線 \(\{P_t\}_{t\in[0,1]}\subset\mathcal{P}(\mathbb{R}^d)\) を直接学習するように発展した．

この方法では，新たな条件付け変数 \(c\in[0,1]^k\) に対して，連続写像 \[ P_{t,c}:[0,1]\times[0,1]^k\to\mathcal{P}(\mathbb{R}^d) \] を学習するようにフローマッチングを拡張できれば，連続な条件付き生成が可能になることになる．

これを行列値ベクトル場の理論を通じて達成するのが 拡張フローマッチング (EFM: Extended Flow Matching) (Isobe et al., 2024) である．

このようなフローマッチングの拡張は (R. T. Q. Chen and Lipman, 2024) でも考えられている．

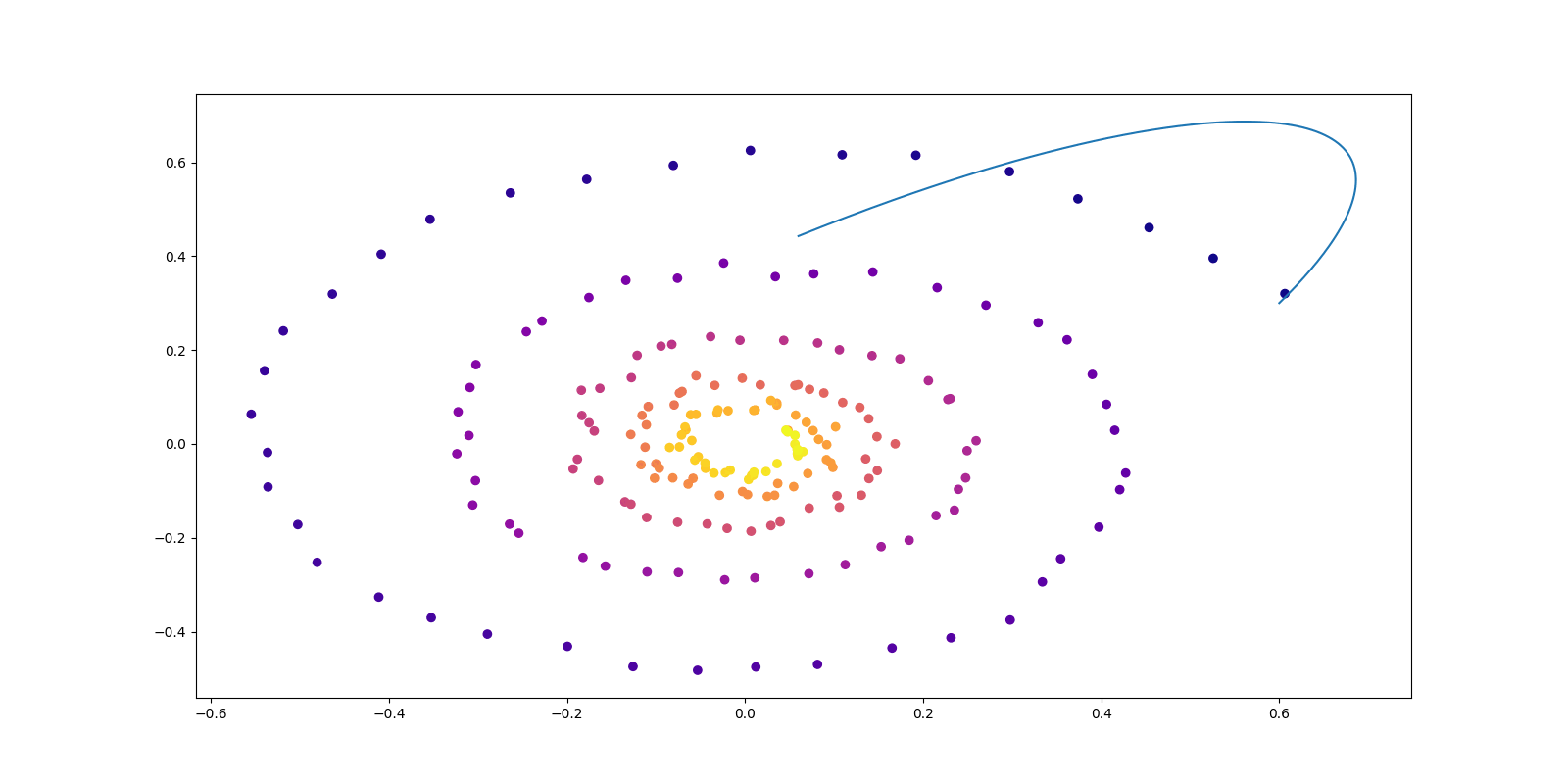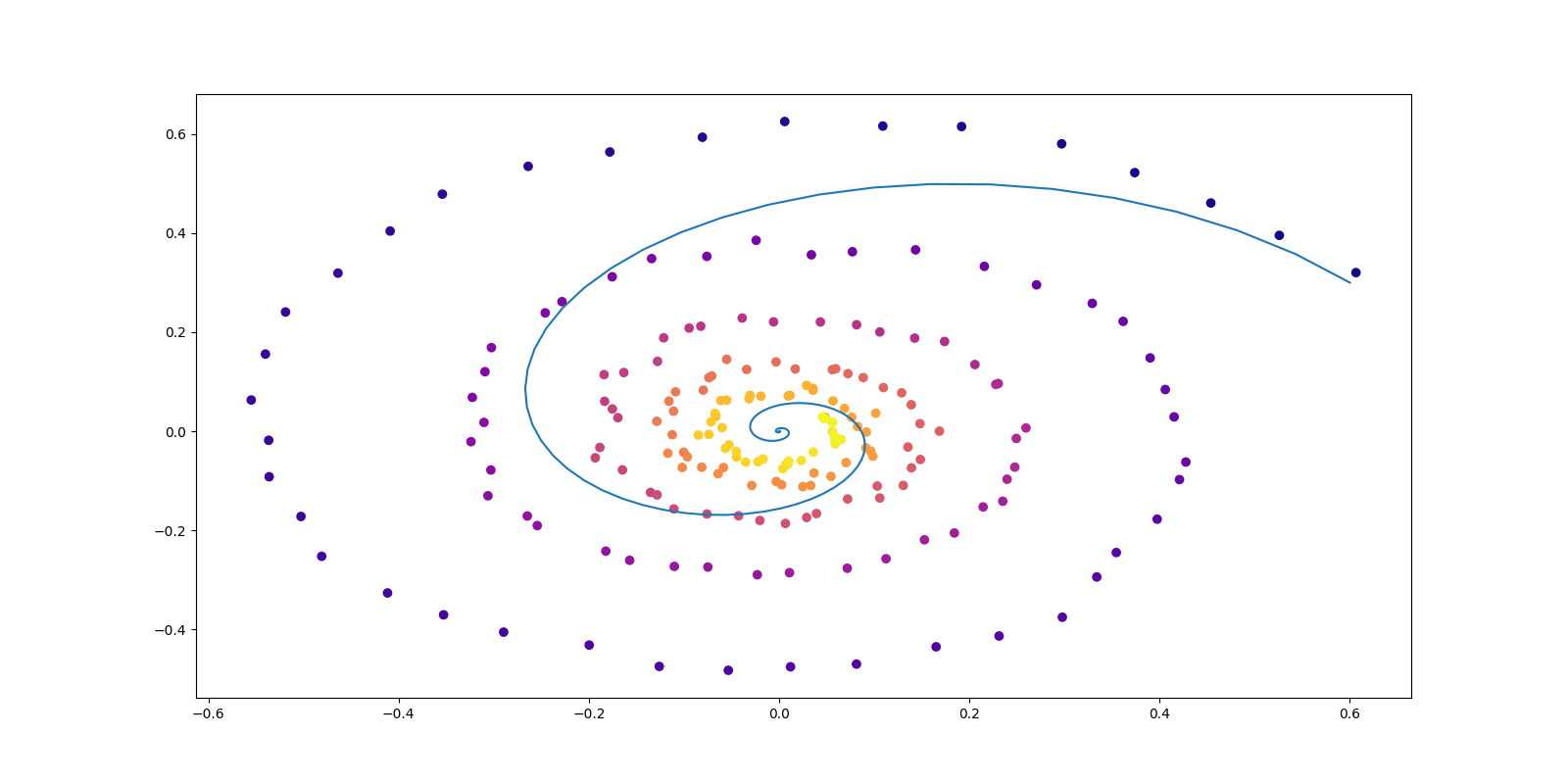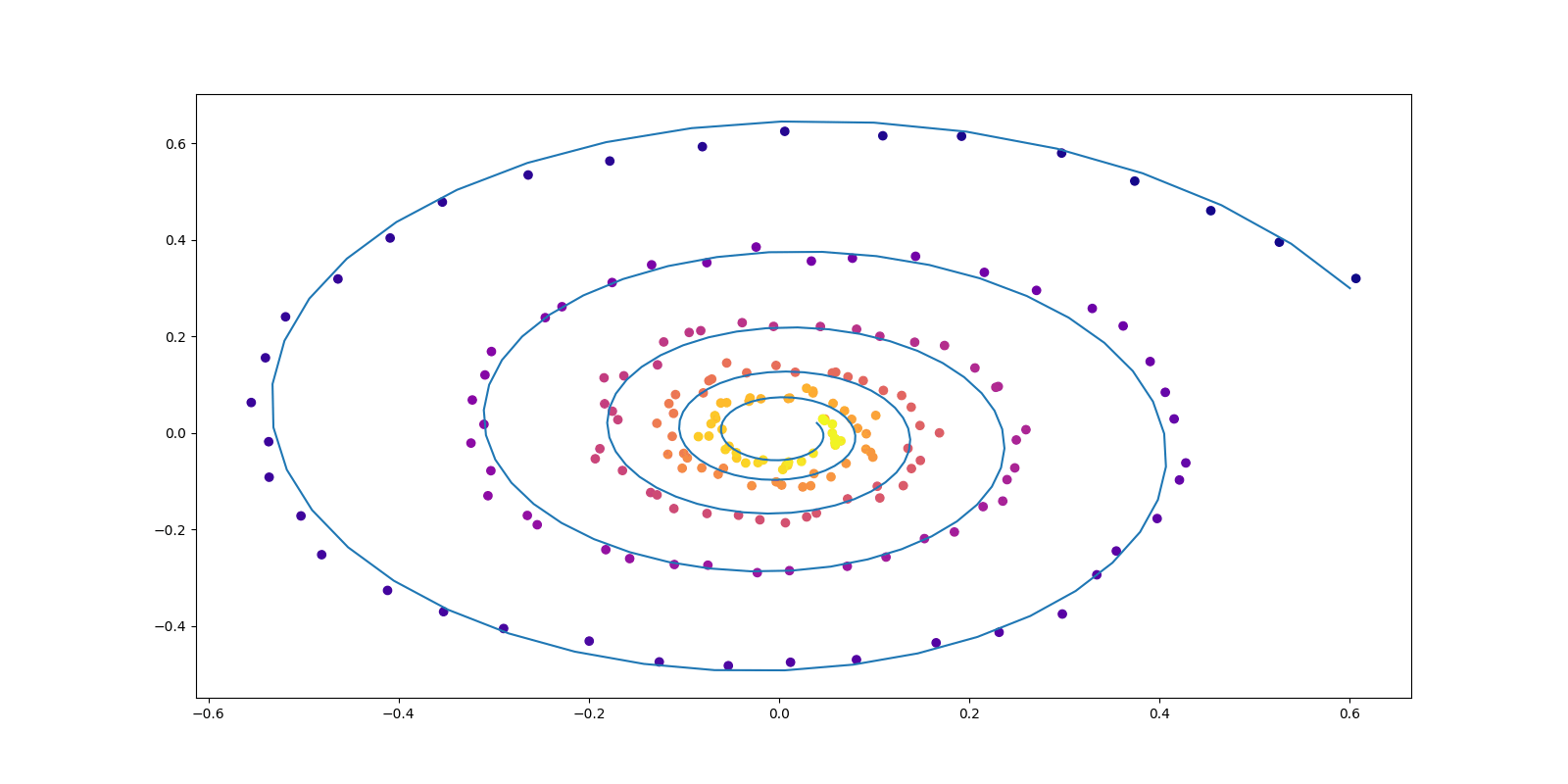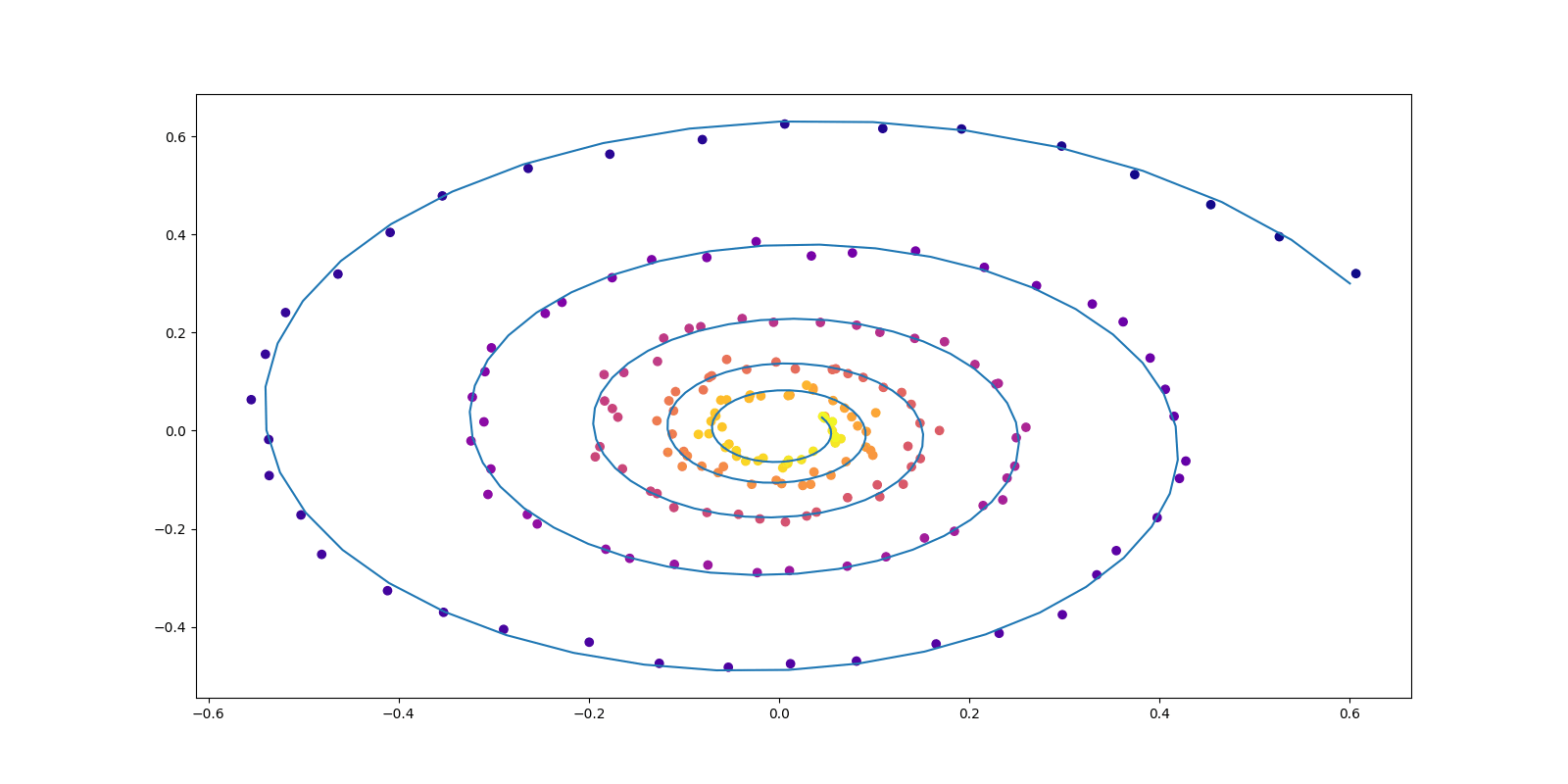
2.2 フローマッチング (FM)

２つの確率分布 \(P_0,P_1\in\mathcal{P}(\mathbb{R}^d)\) を結ぶ曲線を \[ (P_t)=((\phi_t)_*P_0)_{t\in[0,1]}\in\mathcal{P}(\mathbb{R}^d)^{[0,1]} \] の形で学習することを考える．

そのための１つのアプローチとして，連続方程式というPDE \[ \frac{\partial p_t}{\partial t}+\operatorname{div}(F_tp_t)=0. \tag{5}\] を満たすベクトル場 \(F_t\) を学習し，これが定めるフローを \((\phi_t)\) とすることがある：

\[ \frac{\partial \phi_t(x)}{\partial t}=F_t(\phi_t(x)). \]

このような \(F_t\) が１つ既知であり，\(p_t\) から自由にサンプリングできる場合は， \[ \mathcal{L}_{\mathrm{FM}}(\theta)=\operatorname{E}\biggl[\biggl|F_\theta(X_T,T)-F_T(X_T)\biggr|^2\biggr],\qquad T\sim\mathrm{U}([0,1]),X_T\sim p_T, \tag{6}\] の最小化によってベクトル場 \(F_t\) が学習できる．これを フローマッチング (FM: Flow Matching) の目的関数という．

2.3 条件付きフローマッチング (CFM)

仮に \(p_t\) が \[ p_t(x)=\int_\Omega p_t(x|c)q(c)\,dc,\qquad\Omega\subset\mathbb{R}^k, \] という \(p_{t,c}(x):=p_t(x|c)\) の \(q\)-混合としての展開を通じて得られているとする．

この場合，\((p_{t,c})\) を生成するベクトル場 \(F_t(x|c)\) が特定できれば， \[ F_t(x):=\operatorname{E}\left[\frac{F_t(x|U)p_t(x|U)}{p_t(x)}\right] \tag{7}\] が \((p_t)\) を生成する (定理1 Lipman et al., 2023), (定理3.1 Tong et al., 2024)．

従って，\(F_t\) を学習するには FM 目的関数 (6) の代わりに \[ \mathcal{L}_{\mathrm{CFM}}(\theta)=\operatorname{E}\biggl[\biggl|F_\theta(X_T,T)-F_T(X|C)\biggr|^2\biggr],\qquad C\sim q, \tag{8}\] の最小化によっても \(F_t(x|c)\) が学習できる．これを 条件付きフローマッチング (CFM: Conditional Flow Matching) の目的関数という．

\(P_0\) が Gauss 分布である場合 (Lipman et al., 2023)

\(P_0=\mathrm{N}_d(0,I_d)\) をノイズ分布，\(P_1\) を一般のデータ分布とする．

ただし，誤差を許して，\(P_1*\mathrm{N}_d(0,\sigma^2I_d)\) を改めて真のデータ分布とする．

このように定式化することで，各データ点 \(c\in\{x_i\}_{i=1}^n\) で条件づければ， \[ P_{0,c}:=P_0(-|c)=\mathrm{N}_d(0,I_d),\qquad P_{1,c}:=P_1(-|c)=\mathrm{N}_d(0,\sigma^2I_d), \] の間を結ぶ曲線 \((P_{t,c})_{t\in[0,1],c\in\{x_i\}_{i=1}^n}\) を学習する問題となる．

実は \(P_{0,c},P_{1,c}\) が Gauss 分布であることにより，この問題はすでに (McCann, 1997, p. 159) によって解かれており，最適輸送は \[ P_{t,c}=\mathrm{N}_d\biggr(tc,(t\sigma-t+1)^2I_d\biggl),\qquad F_t(x|c)=\frac{c-(1-\sigma)x}{1-(1-\sigma)t}, \] によって与えられる．

しかし，各 \((P_{t,c})_{t\in[0,1]}\) が最適輸送になっていても，式 (7) で定まる \((P_t)_{t\in[0,1]}\) が最適輸送になるとは限らない．

2.4 最適輸送 CFM (OT-CFM)

ここで形式的に，条件付ける変数 \(c\) はカップリング \(\pi\in C(P_0,P_1)\) に従う \(C\sim\pi\) とする： \[ C(P_0,P_1):=\left\{\pi\in\mathcal{P}(\mathbb{R}^d\times\mathbb{R}^d)\:\middle|\:\begin{array}{l}(\mathrm{pr}_1)_*\pi=P_0,\\(\mathrm{pr}_2)_*\pi=P_1\end{array}\right\}. \]

\(P_0\) も一般の分布である場合 (I-CFM Tong et al., 2024)

\(Q_0,Q_1\) は未知のデータ分布で， \[ P_1=Q_1*\mathrm{N}_d(0,\sigma^2I_d),\qquad P_0=Q_0*\mathrm{N}_d(0,\sigma^2I_d), \] の間を架橋したいとする．このとき， \[ \pi:=Q_0\otimes Q_1 \] と定めると， \[ P_{t,c}=\mathrm{N}_d\biggr(tc_1+(1-t)c_0,\sigma^2I_d\biggl),\qquad F_t(x|c)=c_1-c_0, \] が \(P_0,P_1\) の間の輸送を定める (命題3.3 Tong et al., 2024)．

加えて，\(\sigma\to0\) の極限において，学習される輸送 \((P_t)\) は \(Q_0,Q_1\) の間の輸送になる．

これは (Lipman et al., 2023) の例の，\(P_0,P_1\) を対称に扱った拡張と見れる．

また，\(P_{t,c}\) が \(\sigma\to0\) とした Delta 測度である場合が Rectified Flow (Liu et al., 2023) に当たる．

この方法を拡張し，例えば平均を線型関数 \(m(t)=tc_1+(1-t)c_0\) の代わりに \[ m(t)=\cos\left(\frac{\pi t}{2}\right)c_0+\sin\left(\frac{\pi t}{2}\right)c_1 \] とした場合が Stochastic Interpolant (Albergo and Vanden-Eijnden, 2023) に当たる．

その中でも特に，\(\pi\) を 2-Wasserstein 距離に関する最適輸送計画 \[ \pi:=\operatorname*{argmin}_{\pi\in C(P_0,P_1)}\operatorname{E}[\lvert X-Y\rvert^2] \] であるとする．

このとき， \[ P_{t,c}=\mathrm{N}_d\biggr(tc_1+(1-t)c_0,\sigma^2I_d\biggl),\qquad F_t(x|c)=c_1-c_0, \] を \(C\sim\pi\) に関して周辺化した輸送 \((P_t)\in\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) は，\(\sigma\to0\) の極限で（動的な）最適輸送になる (命題3.4 Tong et al., 2024)．

Schrödinger Bridge のシミュレーション (SB-CFM Tong et al., 2024)

\[ \pi_{2\sigma^2}:=\operatorname*{argmin}_{\pi\in C(P_0,P_1)}\biggr(\operatorname{E}[\lvert X-Y\rvert^2]+2\sigma^2H(\pi)\biggl) \] を，エントロピー正則化項 \(2\sigma^2\) を持ったエントロピー最適輸送計画とする．

このとき，各点を結んだ Broanian bridge \[ P_{t,c}:=\mathrm{N}\biggr(tc_1+(1-t)c_0,t(1-t)\sigma^2I_d\biggl), \] \[ F_t(x|c):=\frac{1-2t}{2t(1-t)}\biggr(x-(tc_1+(1-t)c_0)\biggl)+(c_1-c_0), \] の周辺化 \((P_t)\in\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) は，標準 Brown 運動を \(\sigma\) だけスケールした分布 \(W\) に対する Schrödinger bridge \[ \pi^*:=\operatorname*{argmin}_{\substack{\mu_0=P_0\\\mu_1=P_1}}\operatorname{KL}(\mu,W) \] と分布同等になる (定理3.5 Tong et al., 2024)．

\(\sigma\to0\) の極限が OT-CFM であり，\(\sigma\to\infty\) の極限が I-CFM である．

訓練時は，CFM の目的関数 (8) を計算するために \((X_0,X_1)\sim\pi\) というサンプリングが必要になる．データサイズが大きい場合には，これにミニバッチ最適輸送 (Fatras et al., 2021) を用いることができる．

このように，２つの分布 \(P_0,P_1\) を単に独立カップリングと見るのではなく，依存関係があった場合にはそれも考慮してなるべくダイナミクスが直線になるように誘導する方法 Multisample Flow Matching として (Pooladian et al., 2023) も考えている．

2.5 \(\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) 上の最適化としての見方

実は OT-CFM は，２つの確率密度 \(p_0,p_1\) を結ぶ曲線 \((p_t)\in\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) の中で，Dirichlet エネルギー \[ D(p):=\inf_{(p,F)}\frac{1}{2}\int_{[0,1]\times\mathbb{R}^d}\lvert F_t(x)\rvert^2p_t(x)\,dxdt \] を最小化する曲線 \((p_t)\) を学習していると見れる (Isobe et al., 2024)．ただし，\((p,F)\) は連続方程式 (5) を満たす密度とベクトル場の組とした．

条件付きフローマッチングでは，このような曲線 \((p_t)\) を次の方法で構成していた．

ある決定論的なダイナミクス \(\psi_c:[0,1]\to\mathbb{R}^d\) を定める．²
\(Q\in\mathcal{P}(C^1([0,1];\mathbb{R}^d))\) を確率測度とする．
\(\psi,Q\) から， \[ P^Q:=\operatorname{E}_{\psi\sim Q}[\delta_\psi] \] によって確率測度の曲線 \((P^Q_t)\in\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) を定める．

実は Dirichlet 汎函数 \(D:\mathcal{P}(\mathbb{R}^d)^{[0,1]}\to\mathbb{R}_+\) が凸であるために，このように構成される \((p_t)\) の中での最適解は，\(Q\in\mathcal{P}(C^1([0,1];\mathbb{R}^d))\) の全体で探す必要はなく，線型なダイナミクス \[ \psi_c(t)=tc_1+(1-t)c_0,\qquad c=(c_0,c_1)\in\mathbb{R}^d\times\mathbb{R}^d, \] の重ね合わせの形でのみ探せば良い (Brenier, 2003)．

従って，\((X_0,X_1)\) の分布の全体 \(C(P_0,P_1)\) のみについてパラメータづけをして探せば良い．さらにこの場合， \[ F_t(x|c)=\frac{\partial \psi_c(t)}{\partial t}=c_1-c_0 \] であるから，\(D(P)=2W_2(P_0,P_1)^2\) の最小化は \(P_0,P_1\) の 2-Wasserstein 最適な輸送計画 \(\pi^*\) の探索に等価になる．

これが OT-CFM の \(\mathcal{P}(\mathbb{R}^d)^{[0,1]}\) 上の最適化としての解釈である．同時に，条件付きフローマッチングの目的関数 (8) の他に，DSM 様の目的関数 \[ \operatorname{E}\biggl[\biggl|F_T(\psi(T))-\partial_t\psi_C(T)\biggr|^2\biggr],\qquad T\sim\mathrm{U}([0,1]),C\sim\pi^*, \] の最小化点としてもベクトル場 \(F_t\) が学習できる．

2.6 拡張フローマッチング (GFM)

前節での観察は次のように要約できる：

OT-CFM の Dirichlet 汎函数最小化としての特徴付け

OT-CFM は，条件付きフローマッチングに対して，Dirichlet エネルギーの言葉で帰納バイアスを導入することで，最適輸送を学習するための方法論である．

こう考えると，Dirichlet エネルギーの言葉で他の帰納バイアスを導入することが考えられる．

ここで条件付けの議論（第 2.1 節）に戻ってくる．最適輸送のための \(c=(c_0,c_1)\in\mathbb{R}^{2d}\) に限らず，一般の \(c\in\mathbb{R}^k\) に対して連続に条件付けされるように拡張したい．

これは，\((F_t),(p_t)\) の添字を \(t\in[0,1]\) から \(\xi\in[0,1]\times\mathbb{R}^k\) に拡張することで達成される．

これは新たな \((F_\xi),(p_\xi)\) を \(M_{dk}(\mathbb{R})\)-値の行列値ベクトル場 \((F_t)\) とベクトル値密度 \((p_t)\) と見ることに等価である．すると，一般化連続方程式 (Brenier, 2003), (Lavenant, 2019) \[ \nabla_\xi p_\xi(x)+\operatorname{div}_x(p_\xi u_\xi)=0 \] の理論を用いれば，全く同様の枠組みで可能になる (命題1 Isobe et al., 2024)．

これが 拡張フローマッチング (EFM: Extended Flow Matching) (Isobe et al., 2024) である．

2.7 GFM の無限次元最適化

ただし，拡張 Dirichlet エネルギー (Lavenant, 2019) \[ D(P):=\inf_{(p,F)}\frac{1}{2}\int_{[0,1]\times\mathbb{R}^k\times\mathbb{R}^d}\lvert F_\xi(x)\rvert^2p_\xi(x)\,dxd\xi \] の第 2.5 節の形での最小化点は，もはや線型なダイナミクスの重ね合わせとは限らない．

すると無限次元最適化になってしまうため，適切な RKHS \(\mathcal{F}\subset\mathrm{Map}([0,1]\times\mathbb{R}^k;\mathbb{R}^d)\) 内で探すことが必要である： \[ \psi=\phi_{x_{\partial\Xi}}\in\operatorname*{argmin}_{f\in\mathcal{F}}\sum_{\xi\in\partial\Xi}\lvert f(\xi)-x_\xi\rvert^2. \] ただし，\(\partial\Xi\overset{\text{finite}}{\subset}[0,1]\times\mathbb{R}^k\) は境界条件が与えられる点の有限集合で，\(x_\xi\in\mathbb{R}^d\) はその点での値である．

\((\mathbb{R}^d)^{\lvert\partial\Xi\rvert}\) 上での結合分布 \(\pi\) が与えられたならば， \[ \inf_{Q\in\mathcal{P}(C^1([0,1]\times\mathbb{R}^k;\mathbb{R}^d))}D(P^Q)\le\inf_\pi\int_{(\mathbb{R}^d)^{\lvert\partial\Xi\rvert}}\lvert\nabla_\xi\phi_{x_{\partial\Xi}}\rvert^2\pi(dx_\xi) \] という評価が得られるが，この右辺は最適輸送の形になっており，最小値が適切な周辺分布とコスト関数 \[ c(x_{\partial\Xi}):=\int_{[0,1]\times\mathbb{R}^k}\lvert\nabla_\xi\phi_{x_{\partial\Xi}}(\xi)\rvert^2\,d\xi \] が定める輸送計画問題になっている．

この解 \(\pi^*\) をミニバッチ最適輸送で解きながら，目的関数 \[ \operatorname{E}\biggl[\biggl|F_T(\psi(T))-\nabla_\xi\phi_{x_{\partial\Xi}}\biggr|^2\biggr],\qquad T\sim\mathrm{U}([0,1]),x_{\partial\Xi}\sim\pi^*, \] の最小化点としてベクトル場 \(F_t\) を学習することができる (定理4 Isobe et al., 2024)．

これを (Isobe et al., 2024) は MMOT-EFM と呼んでいる．

3 文献紹介

本記事の後半第 2 節は，(Tong et al., 2024), (Isobe et al., 2024) の解説である．

前半の内容に関して，メンダコ氏によるブログ記事 AlphaFold の進化史は AlphaFold3 が丁寧に解説されている．

当該ブログは丁寧に書かれており，大変おすすめできる．

Alphafold3とは長大な条件付けネットワークを備えた全原子拡散生成モデルであると前述したとおり、Alphafold3では必須入力としてタンパク質配列を、任意入力として核酸配列、SMILES形式で表現された低分子リガンド、金属イオンなどを長大な条件付けネットワークに入力することで、拡散モデルへの条件付けベクトルを作成します。

DeepLearningで大規模分子の構造分布を予測するなんて数年前には考えられませんでしたが、拡散モデルによってすでに現実になりつつあります。一例として Distributional GraphormerというMicrosoft Researchの研究 (S. Zheng et al., 2024) を紹介します。

続きはぜひ，メンダコ氏のブログでお読みください．

(Dao et al., 2023) のプロジェクトページはこちら．

References

Abramson, J., Adler, J., Dunger, J., Evans, R., Green, T., Pritzel, A., … Jumper, J. M. (2024). Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature, 630(8016), 493–500.

Albergo, M. S., and Vanden-Eijnden, E. (2023). Building Normalizing Flows with Stochastic Interpolants. In The eleventh international conference on learning representations.

Brenier, Y. (2003). Extended monge-kantorovich theory. In Optimal transportation and applications: Lectures given at the c.i.m.e. Summer school, held in martina franca, italy, september 2-8, 2001, pages 91–121. Berlin, Heidelberg: Springer Berlin Heidelberg.

Chen, R. T. Q., and Lipman, Y. (2024). Flow matching on general geometries. In The twelfth international conference on learning representations.

Chen, T., ZHANG, R., and Hinton, G. (2023). Analog bits: Generating discrete data using diffusion models with self-conditioning. In The eleventh international conference on learning representations.

Chung, H., Kim, J., Mccann, M. T., Klasky, M. L., and Ye, J. C. (2023). Diffusion posterior sampling for general noisy inverse problems. In The eleventh international conference on learning representations.

Dao, Q., Phung, H., Nguyen, B., and Tran, A. (2023). Flow matching in latent space.

Dhariwal, P., and Nichol, A. Q. (2021). Diffusion models beat GANs on image synthesis. In A. Beygelzimer, Y. Dauphin, P. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems.

Ding, X., Wang, Y., Xu, Z., Welch, W. J., and Wang, Z. J. (2021). Cc{GAN}: Continuous conditional generative adversarial networks for image generation. In International conference on learning representations.

Fatras, K., Zine, Y., Majewski, S., Flamary, R., Gribonval, R., and Courty, N. (2021). Minibatch optimal transport distances; analysis and applications.

Ho, J., Jain, A., and Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. In Advances in neural information processing systems,Vol. 33.

Ho, J., Saharia, C., Chan, W., Fleet, D. J., Norouzi, M., and Salimans, T. (2022). Cascaded diffusion models for high fidelity image generation. Journal of Machine Learning Research, 23(47), 1–33.

Ho, J., and Salimans, T. (2021). Classifier-free diffusion guidance. In NeurIPS 2021 workshop on deep generative models and downstream applications.

Isobe, N., Koyama, M., Zhang, J., Hayashi, K., and Fukumizu, K. (2024). Extended flow matching: A method of conditional generation with generalized continuity equation.

Kingma, D. P., Mohamed, S., Jimenez Rezende, D., and Welling, M. (2014). Semi-supervised Learning with Deep Generative Models. In Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, and K. Q. Weinberger, editors, Advances in neural information processing systems,Vol. 27. Curran Associates, Inc.

Krishna, R., Wang, J., Ahern, W., Sturmfels, P., Venkatesh, P., Kalvet, I., … Baker, D. (2024). Generalized biomolecular modeling and design with RoseTTAFold all-atom. Science, 384(6693), eadl2528.

Lavenant, H. (2019). Harmonic mappings valued in the wasserstein space. Journal of Functional Analysis, 277(3), 688–785.

Lipman, Y., Chen, R. T. Q., Ben-Hamu, H., Nickel, M., and Le, M. (2023). Flow matching for generative modeling. In The eleventh international conference on learning representations.

Liu, X., Gong, C., and liu, qiang. (2023). Flow straight and fast: Learning to generate and transfer data with rectified flow. In The eleventh international conference on learning representations.

McCann, R. J. (1997). A convexity principle for interacting gases. Advances in Mathematics, 128(1), 153–179.

Nichol, A. Q., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., Mcgrew, B., … Chen, M. (2022). GLIDE: Towards photorealistic image generation and editing with text-guided diffusion models. In K. Chaudhuri, S. Jegelka, L. Song, C. Szepesvari, G. Niu, and S. Sabato, editors, Proceedings of the 39th international conference on machine learning,Vol. 162, pages 16784–16804. PMLR.

Pooladian, A.-A., Ben-Hamu, H., Domingo-Enrich, C., Amos, B., Lipman, Y., and Chen, R. T. Q. (2023). Multisample flow matching: Straightening flows with minibatch couplings. In A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato, and J. Scarlett, editors, Proceedings of the 40th international conference on machine learning,Vol. 202, pages 28100–28127. PMLR.

Saharia, C., Chan, W., Chang, H., Lee, C. A., Ho, J., Salimans, T., … Norouzi, M. (2022). Palette: Image-to-Image Diffusion Models.

Saharia, C., Chan, W., Saxena, S., Li, L., Whang, J., Denton, E., … Norouzi, M. (2022). Photorealistic text-to-image diffusion models with deep language understanding. In A. H. Oh, A. Agarwal, D. Belgrave, and K. Cho, editors, Advances in neural information processing systems.

Saharia, C., Ho, J., Chan, W., Salimans, T., Fleet, D. J., and Norouzi, M. (2023). Image super-resolution via iterative refinement. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(4), 4713–4726.

Song, J., Zhang, Q., Yin, H., Mardani, M., Liu, M.-Y., Kautz, J., … Vahdat, A. (2023). Loss-guided diffusion models for plug-and-play controllable generation. In A. Krause, E. Brunskill, K. Cho, B. Engelhardt, S. Sabato, and J. Scarlett, editors, Proceedings of the 40th international conference on machine learning,Vol. 202, pages 32483–32498. PMLR.

Tong, A., FATRAS, K., Malkin, N., Huguet, G., Zhang, Y., Rector-Brooks, J., … Bengio, Y. (2024). Improving and Generalizing Flow-Based Generative Models with Minibatch Optimal Transport. Transactions on Machine Learning Research.

Watson, J. L., Juergens, D., Bennett, N. R., Trippe, B. L., Yim, J., Eisenach, H. E., … Baker, D. (2023). De novo design of protein structure and function with RFdiffusion. Nature, 620(7976), 1089–1100.

Zheng, Q., Le, M., Shaul, N., Lipman, Y., Grover, A., and Chen, R. T. Q. (2023). Guided flows for generative modeling and decision making.

Zheng, S., He, J., Liu, C., Shi, Y., Lu, Z., Feng, W., … Liu, T.-Y. (2024). Predicting equilibrium distributions for molecular systems with deep learning. Nature Machine Intelligence, 6(5), 558–567.

Footnotes

\(c\) が \(x_t\) と同じ画像である場合は，(Ho et al., 2022) のように \(x_t\) にそのまま連結することも考えられる．↩︎
すべての \((P_{t,c})_{t\in[0,1]}\) は \(\sigma\to0\) の極限で決定論的なダイナミクスを定めていた．これを \(\psi_c(t)\) と表すこととする．↩︎