俺のための Julia 入門（１）データ型

データ型とその上の原始関数

Julia
俺のためのJulia入門
Author

司馬 博文

Published

9/06/2020

Modified

7/04/2024

概要
Julia は動的型付け言語で，型宣言 :: を省略すると全てのオブジェクトとマッチする Any 型と解釈される．一方で静的型付け言語のような豊かな型システムも持つ．これにより関数をメソッドのディスパッチにより実装するのが Julia の根幹思想である．メソッドのディスパッチについては次稿に譲り，ここでは基本的なデータ型について述べる．
Julia の多重ディスパッチを中心とした関数志向設計
  1. 動的型付けであるが，明示的な型付けを型注釈の記法でコードに追加できる．
  2. 多重ディスパッチによって動的にメソッド呼び出しが行われる．Julia で method というと，この多重ディスパッチの方を意味する．1
  3. 一般的な OOP ではなく，オブジェクトに関数を所属させる意味での method は存在せず，型の継承も存在せず，階層関係があるのみである．
Julia のデータ型
  • 全ての型は supertype をもち，Julia の Type はこの親子関係について木構造をなす．
    • root はAnyである．
    • 多重ディスパッチでは，より葉に近い方から match する．
  • concrete型とabstrat型に大別される．
    • concrete型の中でも基底層であるprimitive型は 8bit 単位で指定する．
    • abstract型は instance 化して object を得ることはできない．
    • concrete型はsubtypeを持てない．

1 Built-in Type@base/boot.jl

Types (Julia Manual)

組み込み型一覧

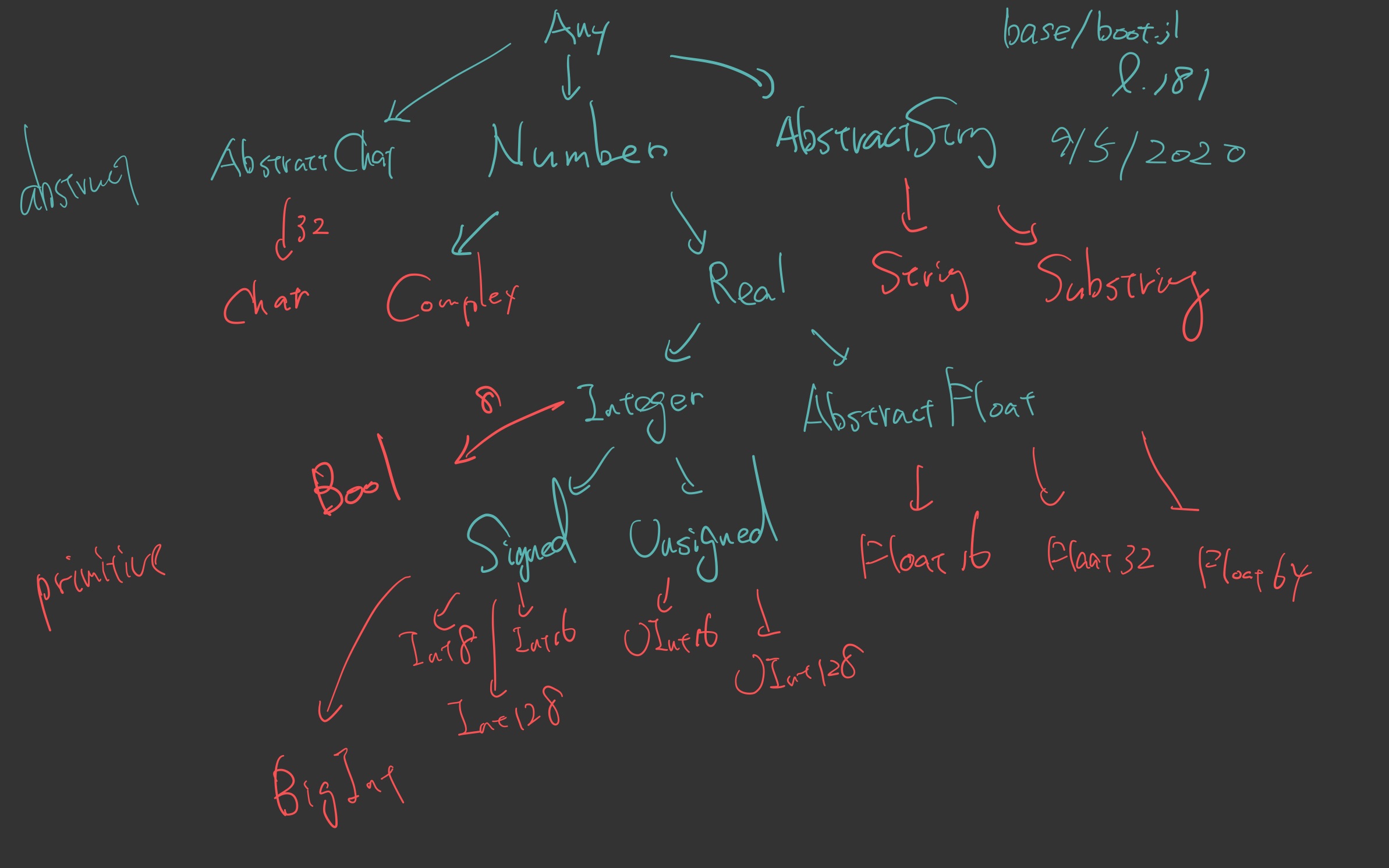
  • Julia の型木 (type tree) において，具体型はすべて葉になり，他の型の親にはならない．

    この機能は Julia の多重ディスパッチと併せて，「構造は受け継がないが機能は継承される」型システムが実現される．

2 原始型

  • Nothing型 <: Any

    • ただ一つの instance であるnothingを持つ．
    • subtypes を訊くと Type[]と返ってきた．
    • nothing objectはREPLでは何も表示されない．return [nothing]と同じ原理．新たな空の概念ですね，記号論が出来る．

  • isnothing(x) -> ::Bool

  • 整数ℤ

    • Int8, UInt8, Int16, UInt16, Int32, UInt32, Int64, Uint64, Int128, Uint128
    • Int, UInt型：システムのデフォルトSys.WORD_SIZEに応じて，上記のいずれかのエイリアスとして設定されている．僕のMacは64bitなので64．
    • 符号なし整数型はprefix”0x”を付けて十六進法で表す．
    • ÷/2
      • 整数除算
      • %の共役というか．

  • 真理値TV={true, false}

    • Bool
    • !
      • 論理否定
    • ~
      • bit not
    • &
      • bit and
      • bit or
    • ⊻ (+ Tab)
      • bit xor
      • 右論理シフト
      • 右算術シフト
    • <<
      • 左論理／算術シフト ＊論理演算はassembly言語の包みと考えるのが良い． 論理演算：word(charやintなど)では届かない，個々のbitに対する演算に対するinterfaceを実装するためにISAや言語に追加された命令操作．初期のコンピュータは「語」単位でデータを扱っていたが，そんなの粒度大きくて仕方がない，という歴史的経緯で後から追加された群．C言語では1bitまで小さいfieldを取れる．（こういう”field”の使い方を，”bit field”という．）
    • shift : 語中の全てのbitを左や右にずらして，空いた部分には０を詰める．n bitの左/右シフトは，2^(±n)を乗ずることに等価．だから，実は配列のindexからbyte addressingに換算してどれくらいbaseからとぶかの計算は，左２シフトである．CやJavaの<<に当たる．
      • AND : 以前はmaskと呼んでいた，隠すからである．maskはAND論理演算のことだったのか！高級言語の&
      • OR, NOR(=ORのNOT) : 左から作用すると考えればちょうどNOT◦OR．それぞれ高級言語の:, ~(これは本来ORの実装)にあたる．
        • NOTはNORを使われて，ISAには等価なものはない．
    • ===
      • メモリ上のobjectとしての同一性．
      • こんな意味論数学上にはない．

  • 小数

    • Float16, Float32, Float64
    • 通常は64で解釈され，32はf0やf-4のsuffixを付けて表す．
    • それぞれのサイズに対して，値Inf16, Inf32, Infが無限大を表す値として用意されている．
    • 0/0などの「未定義」値として，NaN16, NaN32, NaNが用意されている．
    • /2
      • x/yの共役演算

  • 複素数ℂ

    • 虚数単位はim
    • real(x)
    • imag(x)
    • conj(x)
    • abs(x)

  • 任意精度演算

    • 任意精度整数：BigInt，任意精度小数：BigFloat

  • 定数

    • 宣言constをつけてから定義する．
    • 組込定数
      • pi
      • VERSION

3 Collection型：直積

更なる構造付きのものはDataStructure.jlにある． 各直積型に，tagをつけてその性質を明示する．

3.1 Collection 型

全てのobjectに，indexing, slicingの操作が施せる．

indexing - [n] - 最初から数えて第n byteのobjectを返す． - 日本語は3byte表現されていることに注意． - [end] - 最後の要素のindexing．長さがわからないときに使う． - [end-n] - 末尾からのindexing slicing * n:m * UnitRange{Int}型object． * for文にも使える． - [n:m] - n番目からm番目までの閉区間を切り取る． - n=mの時，indexingとは違ってString型を返す．

  • 文字列
    • Char, String
      • UTF-8符号化を用いているので，Unicode文字列がサポートされている．
        • UTF-8は可変長の符号化なので，indexingについては注意しなきゃいけない．
    • “ … “ #constructor
      • String型を作る．
    • ‘ … ‘ #constructor
      • Char型を作る．
        • 連結演算子
    • string(x[,y,…])
      • 連結コンストラクタ．
    • $
      • 文字列補間(interpolation)演算子
      • $(obj)で，objに格納されたString型オブジェクトに置換される．
      • $(1+2)は評価されてから文字列に変換される．
    • Vector{Char::DataType}(s::String) -> Array
      • Charと指定したデータの配列にデータ型を変換する．するとindexingが直感的にやりやすくなる．
      • これはconstructorに(s)で作用させているのか．
    • length(s)
    • repeat(s,n::int)
    • replace(str, s => t)
      • 論理でいえばstr[s::=t]
    • split(str, delimitar) -> Array{SubString{String}, n}
      • delimitarの部分で分割し，n要素のString-配列を返す．
    • startswith(str1, str2) -> TV::Bool
      • str1がstr2の文字列を始切片として持つ場合trueを返す．
    • endswith(str1, str2)
    • join([str1, str2]::Array{String}, delimitar} -> String
      • delimitarで区切りながら連結
    • findfirst(str1, str2) -> slicing object::UnitRange{Int64}
      • str1の先頭から，str2にマッチする部分を検索し，見つかったらその最初の要素の範囲を閉区間で返す．
  • 正規表現object::Regex
    • 文字列型データの前にrをつけることで表す．
    • PCRE (Perl compatible regular expressions)ライブラリでサポートされている．
    • match(regex::Regex, string) -> RegexMatch(“substring”::Substring{String})::RegexMatch
      • matchingがなかった場合はnothing::Nothingが返ってくる．
  • RegexMatch
    1. m.match::Substring{String}：matchした文字列が格納されている．
    2. m.offset::Int：マッチした位置を表すindexが格納されている．
  • 配列

3.2 Any直下の型

  1. (a,b,…)::Tuple{T1,T2,…}
    1. immutableである
    2. Array型に対するsize関数の返り値はTuple型．
    3. 可変長引数もTuple型のobjectとして受けられる．
    4. 上記から観察されるように，入れ物であって，代数的構造を持たせることを意図していない．その場合はArrayを使う．
  2. named tuple：Typeの直積．
    1. 元々NamedTuple.jlという独立したpackageだったが，0.7から統合．
    2. 要素に数字以外のaliasでタグ付できる．immutable．
    3. (a=1, b=2)::NamedTuple{(:a, :b), Tuple(Int, Int)}などの記法で定義される．
    4. つまり，値のTupleと，Symbol型のオブジェクトのTupleとの組で表される．
    • この時の射影が，keys関数，values関数として実装されている．
    1. keyは.演算子でアクセスできる．
      • t.a
    2. Symbolをindexの代わりに使える．
      • t[:a]
    3. 一時的に使うのが普通で，本格的にはstruct, mutable structとして第一級の居住権を与えるのが良い．
  3. List：Array{T,1}としての実装．Vector{T}というエイリアスもある．
    1. 追加や削除などの順序的構造が重視されるCollection型．
    2. スタック，キュー，両端キューはDataStructure.jlへ．
    • push!(List, object) -> List’
      • 要素の末尾追加
    • pushfirst!(List, object) -> List’
      • 要素の先頭追加
    • pop!(List) -> object
      • 要素の末尾摘出
    • popfirst!(List)
    • insert!(List, n, object) -> List’
      • n番目の位置に追加
    • deleteat!(List, n) -> List’
      • n番目の要素を削除．
  4. 辞書：Dict{K, V}という直積型
    1. constructorは
      • d = Dict{String, Int}()
      • d[“a”] = 1
      • d = Dict(key => value, key => value, …)
    2. constructorの{}内の要素を１つ，または全て省略するとAnyとしたのと等価．
    • haskey(Dict, key) -> Bool
      • Dict型objectに，所定のkeyが含まれているかを判定する．
    1. built-inにIdDict型とWeakKeyDict型がある．
  5. 集合：Set{T}
    1. constructorは
      • s = Set([1,2])
    2. 即ち，１次元Arrayから生成される．というより，１次元Arrayにタグをつけたものである．
    3. 実装は「keyのみを保持する辞書」というべきもので，辞書と同様，値の重複を無視する．
    • push!(set, object)
      • 値の追加．
    • union(set, List)
    • intersect(set, List)
    • issubset(List, List) -> ::Bool
    • List ⊂ List -> ::Bool
      • Set型のinstanceを生成することなく集合演算ができる．
  6. 多次元配列：Array{T,n}．Matrix{T}はArray{T,2}のエイリアスである．
    1. MATLABを踏襲している．NumPyとは所々違う．
      1. NumPyは0からindexingし，row-major orderである．これは，行列のindexingにとって，辞書式順序になる．
      2. しかしJuliaは1からindexingし，column-major orderである．後者は行列のindexingに沿って，第一要素のストライドが１になる．
        1. 従って，Juliaは同じ行の要素の列挙が得意．線型代数のものの見方である．
    2. 内部実装は結局一次元配列（List）であることを意識すると良い．
  • [] (constructor)
    • [ a b c; d e f; h i j ]
    • または改行を入れてもいい．
  • []
    • 要素へアクセスする作用素．
  • isempty(collection) -> Bool
  • empty!(collection) -> collection
    • 空にする
  • length(collection) -> Int
  • eltype(collection) -> Type
  • 関数名の最後に!
    • 引数の一部を変更・破棄する関数
    • !のつかない関数は，引数に対する破壊的変更はないので安心して使用できる，という慣習．
    • 例：push!，insert!
    • sortは新たなobjectを返すが，sort!は引数そのものを変更してしまう．
  • for文に使う構文はPythonと同じ使用感．
    • しかし，直積型を意識．
      • for (key, value) in d::Dict
    • 実装は，iterable型オブジェクトを介して行われる．つまり，Juliaは次のように変換して処理される．速度の問題？
      • next = iterate(collection)while next !== nothing　　(x,state) = next　　#suite　　next = iterate(collection, state)end
    • Juliaはiterable型は無く，Tuple{Int, Int}である．
      • 第一要素は，「次の要素」で，第二要素は「その次の要素」のindex（やそれに値するもの）を表す整数またはnothing．
    • 従って，自作のcollection型にもfor文iterationを実現させるためには，iterate関数をディスパッチすれば良い．

4 Array型の関数

4.1 作成

  1. constructor
    1. Array{T}(undef, dims…)
      1. 値が初期化されていないことに注意．
    2. collect(reshape(1:9, 3, 3))
      1. collectionから，要素を奪って配列に仕立て直す．
  2. zeros([T,] dims…)
  3. ones([T,] dims…)
  4. fill(x, dims…)
    1. 行列xI
  5. fill!(A,x)
    1. 配列AをxIにする．
  6. rand([T,] dims…)
    1. 一様分布でランダムに初期化した配列
    2. 型を指定しないとFloat64で．
  7. randn([T,] dims…)
    1. 正規分布でランダムに初期化した配列
  8. similar(A,[T,dims…])
    1. 配列Aと類似した配列を返す．
  9. reshape(A, dims…) -> AbstractArray
    1. 切り取る，または形を変える．
    2. 並びはcolumn-major orderのままである．
    3. AにはUnitRange型も許容されるのがすごい．
  10. copy(A)
  11. deepcopy(A)
    1. Aの要素も再帰的にコピーする．
  12. [A B]
    1. 数学的記法の感覚で使える行列の接続．
  13. view(A, n, m) -> view(::Array{T,n}, m, i)
    1. n, mはindexingまたはslicing．
    2. Aから部分配列を抜き出す．
    3. 返るobjectはAへの参照とindexの情報を持っているので，Aを変更するとその部分配列も変わる．
      1. この実装は，Aが巨大すぎる場合への配慮を感じる．
      2. 「ただし，現在の計算機による配列のコピー操作は，一般に非常に高速であるため，巨大な配列を扱うのではない限り，サブ配列を作成するよりも，通常のindexingで新たな配列を作成してしまう方が高速であることも多い．この辺りは，実際に計測してパフォーマンスを確かめてみるのが良いだろう．」

4.2 属性

  1. eltype(A)
  2. length(A)
  3. ndims(A)
  4. size(A)
  5. size(A,n)
    1. n番目の次元におけるAのサイズ
    2. size(A)で返ってくるtupleの第n要素．
  6. strides(A)
    1. Aのストライド．
    2. 第一要素は必ず１になる．
    3. 要素同士が，一番浅い意味での一次元配列上でどれくらい離れているか．
  7. stride(A,n)
    1. n番目の次元におけるAのストライド
  8. [i, j, k, …]または[n:m, i:j, k:l, …]でindexingできる．

4.3 代数的構造

      1. 行列乗算

dot付演算子：broadcasting．broadcast(+, A, B)のエイリアスである．broadcast!(+, A, B)とするとAが変更される．

  1. component-wiseの演算．
    1. A .+ c
      1. A + cIと同じ．
  2. column-wiseの演算．
    1. A .+ B
      1. BがAの繰り返し単位になっている場合のみ．
      2. つまり，size(B)とsize(A)を各要素ごとに見比べたとき，次の２条件のいずれかを満たすとき．
        1. 値が同じ
        2. どちらかの値が１
      3. ２つ目の条件として，pr_i(size(B)) | pr_i(size(A))だったらもっと使いやすかったがね．
  3. broadcast関数
    1. broadcast(f, args…)が定義．
    2. f.(args…)とも記述できる．
      1. ただし，f=+などの時には使えない．fは関数が想定されている．
      2. sigmoid.(A)やexp.(A)などである．
    3. argsはArrayに限らず，tupleでも良い．

4.4 位相的構造

  1. map(f, c::collection…) -> collection
    1. collection cにelement-wiseにfを適用させる．
    2. broadcastingやdot演算と似ているが，fが匿名関数でない場合はdot演算を使うのが良い？
  2. reduce(op, itr; [init]) -> obj
    1. Aをitrableと見做して，要素ごとにopに突っ込んでいく．
    2. 従って，次元が１段階下がる．
  3. filter(f, a::collection) -> a’
    1. aを要素ごとにfに突っ込んで，fがfalseを返すものについては脱落させる．

Footnotes

  1. Julia でメソッドというと関数の多重ディスパッチのことであり，特定のクラスへの所属を含意しない．この意味で，Julia はオブジェクト志向というより関数志向・プロセス志向である．Stefan Karpinski (2019) The Unreasonable Effectiveness of Multiple Dispatch も参照．↩︎