最適輸送とは何か？

歴史と概観

P(X)
Survey
Author

司馬博文

Published

9/03/2024

Modified

10/06/2024

概要
最適輸送問題は変分法の黎明期に提案された変分問題の１つであるが，その発展は確率論の成熟を待つ必要があった．現代では多くの非正則な空間上に幾何学的な量を定義する普遍的な手法として理解されてから，多くのフィールズ賞受賞者を輩出する最も活発な分野の１つとなっている．ここまでの発展の歴史を本記事では概観したい．

最適輸送に関する記事

はじめに

最適輸送問題は，変分法の黎明期に提案された，変分問題の１つである．

しかし，Lagrange と Hamilton による解析力学の変分原理や，Plateau 問題から続く極小曲面の理論と違い，最適輸送問題は変分法の黎明期に提案されたにも拘らず，その発展は大きく遅れた．

実際，(Monge, 1781) の問題が解かれたのは (Brenier, 1987)，(Kantorovich, 1942) が拡張した形が厳密に解かれたのは独立な結果 (Evans and Gangbo, 1999), (Ambrosio, 2003) まで待つ必要がある．

そこで，本章では変分法の歴史（第 1 節）を見ることから始め，続いて (Kantorovich, 1942) の定式化と双対性理論を見る（第 2 節）．

Kantorovich の問題は離散空間上に限っていたが，一般の Polish 空間上の理論を第 3 節でみる．最後にまとめる（第 4 節）．

1 変分法の始まり

変分法 (calculus of variations) とは，関数空間上の関数（汎函数という）の最適化問題をいう．

1.1 Fermat の原理

歴史上，最初に解析的な解答が与えられた変分法の問題は Fermat の原理 (Fermat, 1657) である (Goldstine, 1980)．

これは 光の経路は，進むのにかかる時間が停留するような曲線として実現される というものであり，この原理から光の直進性や反射・屈折の法則が導かれる．

実は約 200 年後の Hamilton は，自身の名前も冠されている Hamilton 力学の研究の前に光学の研究を行なっている．

そこで光の反射・屈折などの法則から Fermat の原理を逆に導き，２つの定式化が等価であることを導いた (中根美知代, 2000)．その際に用いた表現が「特性関数」と呼んだ汎函数 \(I\) に関する変分原理 \[ \delta I=\delta\int\nu(x,y,z)\,d\rho=0 \] である．ただし \(\nu\) は屈折率，\(\rho\) は線分要素であり，\(\delta\) は Lagrange の変分作用素である．

Hamiltonian はこの定式化を光学から力学に拡張し，Hamilton 形式の力学となった．現代では Hamiltonian と呼べる量は (Hamilton, 1834) で最初に出現し，「主関数」と呼ばれている (中根美知代, 2000)．主関数 \(I\) に対して \(\delta I=0\) が成り立つことと，Euler-Lagrange 方程式が成り立つことが同値になる．1

1.2 最急降下問題

続いて (Bernoulli, 1696) にて John Bernoulli が 最急降下曲線 (Brachistochrone problem) 2 を自身の著書で取り上げた．

「誰も答えられなかった場合は自分の回答を発表する」というスタイルが挑戦的で，Leibniz, Newton など多くの数学者がこれに取り組んだ．John 自身は「最速の粒子の軌道は光と同じ原理で進むはずだ」との仮定から，Fermat の原理の繰り返しと見ることで幾何学的にこの問題を解いた (Levi, 2014)．

同時に関連する複数の「変分問題」を発表した．これを (Euler, 1744) が組織的に取り上げるとともに，変分法 の名前をつけた．

命題（最急降下曲線）

\[ \Omega:=\left\{\gamma:[t_0,t_1]\to\mathbb{R}^2\;\middle|\;\begin{array}{l} \gamma(t_0)=(0,0),\gamma(t_1)=(a,b).\\ C^1\text{級の陰関数表示}y:[a,b]\to\mathbb{R}_+\text{を持つ}\\ \gamma'(t_0)=(0,0). \end{array}\right\} \] 上で，一様重力下で原点からより低い位置にある点 \((a,b)\;(a<0,b>0)\) に最も速く移動する曲線は，次の cycloid が与える： \[ \gamma(t)=C\begin{pmatrix}t-\frac{\sin 2t}{2}\\\frac{1}{2}-\frac{\cos 2t}{2}\end{pmatrix},\qquad C>0,t\in[0,t_1],Ct_1-\frac{\sin 2t_1}{2}=a. \]

まず，所要時間を表す汎関数 \(S:\Omega\to\mathbb{R}\) を求める．

位置 \(x\) での速さを \(v(x)\) とすると，初期条件 \(v(0)=0\) より，エネルギー保存則から \[ \frac{1}{2}mv(x)^2=mgy(x) \quad\Leftrightarrow\quad v(x)=\sqrt{2gy(x)}. \] 位置 \(x\) までの運動の軌跡の長さ \(l(x)\) は \[ l(x)=\int^x_0\sqrt{1+y'(x)^2}dx \] である．以上から， \[\begin{align*} S(\gamma) &= \int^{l(a)}_0\frac{dl}{v(x)} \\ &= \int^a_0\frac{\sqrt{1+y'(x)^2}}{v(x)}dx = \int^a_0\sqrt{\frac{1+y'(x)^2}{2gy(x)}}dx. \end{align*}\] 改めて，\(S(\gamma)\) の \(\sqrt{2g}\) 倍を \(S(\gamma)\) として取り直しても，極値点は変わらない． 特に，Lagrangian は \[ L(y,y'):=\sqrt{\frac{1+y'^2}{y}} \] で与えられる．

計算すると， \[ \frac{\partial L}{\partial y}=\frac{1}{2}\left(\frac{1+y'^2}{y}\right)^{-\frac{1}{2}}\left(-\frac{1+y'^2}{y^2}\right)=-\frac{1}{2}\frac{(1+y'^2)^{\frac{1}{2}}}{y^{\frac{3}{2}}} \] \[ \frac{\partial L}{\partial y'}=\frac{1}{2}\left(\frac{1+y'^2}{y}\right)^{-\frac{1}{2}}2\frac{y'}{y}=\frac{y'}{\sqrt{y(1+y'^2)}} \] から，Euler-Lagrange 方程式は \[\begin{align*} -\frac{1}{2}\frac{(1+y'^2)^{\frac{1}{2}}}{y^{\frac{3}{2}}} &= \frac{d }{d x}\frac{y'}{\sqrt{y(1+y'^2)}} \\ &= \frac{y''}{\sqrt{y(1+y'^2)}}+\left(-\frac{1}{2}\right)\frac{y'}{\biggr(y(1+y'^2)\biggl)^{\frac{3}{2}}}\biggr((1+y'^2)+2yy'y''\biggl) \\ &= \frac{y''}{\sqrt{y(1+y'^2)}}-\frac{1}{2}\frac{y'}{\sqrt{y^3(1+y'^2)}}-\frac{y'^2y''}{\sqrt{y(1+y'^2)^3}}. \end{align*}\] となる．両辺に \(\sqrt{y(1+y'^2)}\) を乗じることで \[\begin{align*} -\frac{1}{2}\frac{1+y'^2}{y} &= y''-\frac{1}{2}\frac{y'}{y}-\frac{y'^2y''}{1+y'^2} \\ &= \frac{y''}{1+y'^2}-\frac{1}{2}\frac{y'}{y} \end{align*}\] より， \[ -\frac{1}{2y}=\frac{y''}{1+y'^2} \quad\Leftrightarrow y'^2+2yy''+1=0 \] の形に同値変形出来る．同値性は因子 \(y(1+y'^2)\) が \(x=0\) の場合を除いて零にならないことによる．

この常備分方程式には積分因子 \(y'\) が見つかり，これを両辺に乗じることで \[ y'+2yy'y''+y'^3=(y+yy'^2)'=0 \]

を得る．よって，この第一積分を \(y+yy'^2=C>0\) とおいて解を求める．なお，\(y\ge 0\) として良いから \(C\ge0\) が必要で，\(C=0\) のとき \(y=0\) より \(\Omega\) の元ではない．この条件は正規形の常微分方程式 \[ y'=\sqrt{\frac{C-y}{y}} \] に帰着するが，これは変数分離型であることに注目すれば， \[\begin{align*} x &= \int\sqrt{\frac{y}{C-y}}dy+C' \qquad C'\in\mathbb{R}\\ &= \int\frac{\sin t}{\cos t}2C\sin t\cos tdt+C' \qquad y=:C\sin^2t \\ &= C\int(1-\cos 2t)dt+C' \\ &= C\left(t-\frac{\sin 2t}{t}\right)+C'. \end{align*}\] と積分出来る．\(y=0\) のとき \(t=0\) で，このとき \(x=0\) が必要だから，\(C'=0\) を得る． 総じて， \[ \begin{cases} x=Ct-\frac{C}{2}\sin 2t, \\ y=C\sin^2t=\frac{C}{2}-\frac{C}{2}\cos 2t. \end{cases} \qquad C>0. \]

1.3 Euler の直接法

(Euler, 1744) は曲線全体の集合 \[ \Omega(x_0,x_1):=\left\{\gamma\in C^\infty([t_0,t_1])\,\middle|\,\gamma(t_0)=x_0,\gamma(t_1)=x_1\right\} \] 上の汎函数 \[ S(\gamma):=\int^{t_1}_{t_0}L\circ\gamma\,dt \] の極値を求める一般的な方法（のちに Euler-Lagrange 方程式として知られる）を示し，それを 100 以上の具体的な問題で検証した (Goldstine, 1980)．

しかし (Euler, 1744) は専ら幾何学的な手法を用いており，「幾何学的でない方法の開発が望まれる」という但し書きが p.52 に付けられているという．

これに対して当時 19 才であった Lagrange が Euler に自身のアイデアを手紙に綴り，すぐさま非凡なアイデアを感得した Euler は Lagrange を呼び出した．

Lagrange の方法は，変分作用素 \(\delta\) を用いた完全に代数的なもので，実際 (Lagrange, 1788) は一才の図表や幾何学的な議論がなく，Newton 力学が完全に代数・解析化されている．

Euler ものちに Lagrange の方法が優れていることを認め，自身のスタイルを完全に Lagrange の方法に移した．

一方で近年，Euler の方法は具体的な構成を与えることと，数値解法との相性が良いことから，直接法 (direct method) として復活を見ている (Hanc, 2017)．

1.4 Plateau 問題

Lagrange は 1760 年に，与えられた境界条件を満たす曲面の中で面積が最小になるものを決定するという，現代でいう プラトー問題 を定式化した．

これは現在でも変分法の中心問題の一つである．特に，一般の \(n\) 次元 Euclid 空間内の \(k\) 次元曲面に関するプラトー問題は，\(k\le n-2\) の場合や \(n\ge8\) の超曲面の場合に解が滑らかでないことがある．

1.5 最適輸送問題

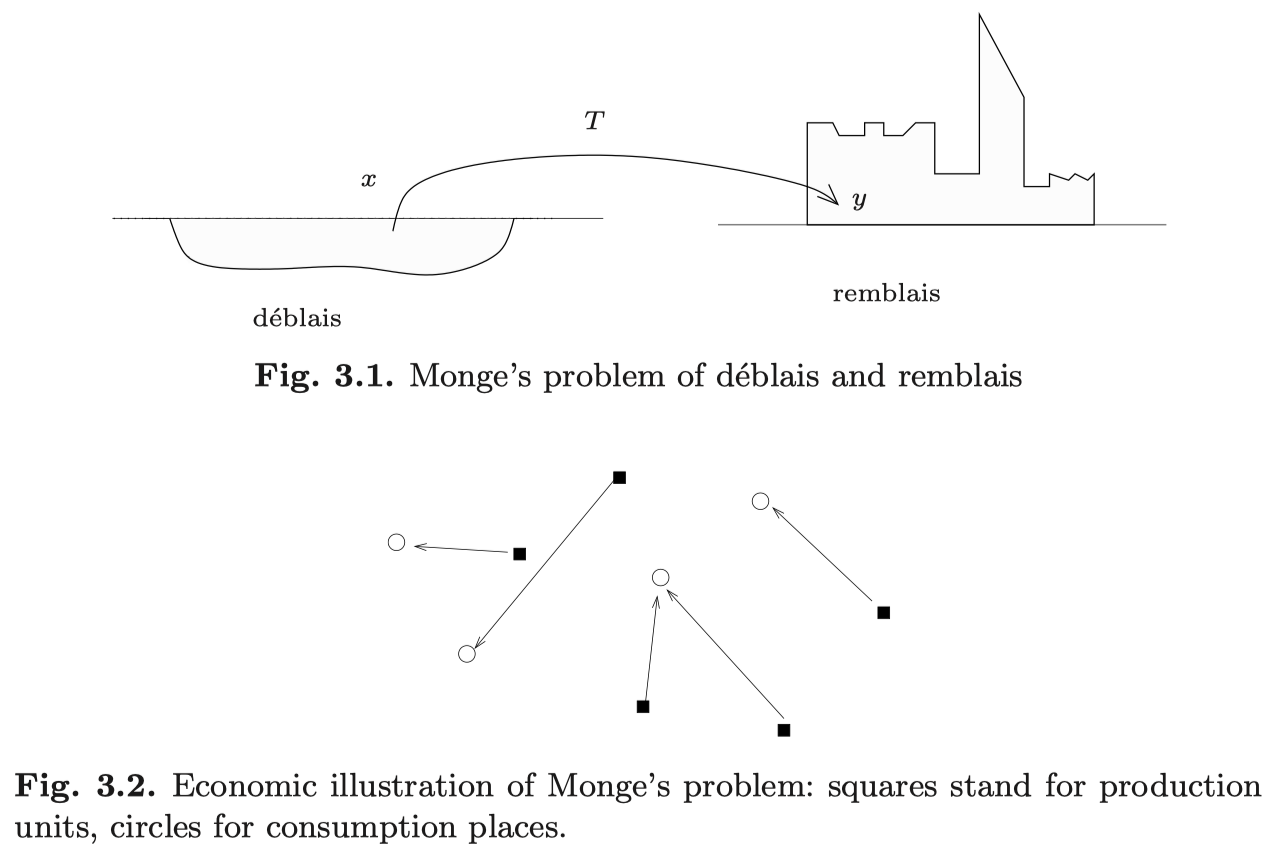
最適輸送の問題はフランス革命の最中に (Monge, 1781) によって考えられた．

論文のタイトルにある déblai とは掘削現場の残土のことであり，remblai は建築時の盛り土を指す．

掘削現場と建築現場が分離している際に，どの地点からどの地点に土をどれほど運べば，最もコストが低く済むかを考えることが Monge の問題である．

(Villani, 2009, p. 30)

現代的には \(\mathbb{R}^3\) 上のコスト \[ c(x,y):=\lvert x-y\rvert \] に関する最適輸送問題である．

しかし (Monge, 1781) では決定論的な解，すなわち「１箇所の掘削現場の土は全て同一の現場に輸送し，複数箇所に分割して輸送することはない」という状況に限って考察していた．

1.6 最適輸送問題の特殊性

しかし，曲線や力学の変分問題や Plateau 問題とは異なり，(Kantorovich, 1942) が独立に定式化するまで，ほとんど目ぼしい発展はなかったのである！

これは他の問題と比べて確率論が重要な位置をしめるため，特に定式化が難しかったためだろうと考えられる (Ambrosio and Quarteroni, 2024)．実際，公理的な確率論の展開は (Kolmogorov, 1933) まで待つ必要があった．

実際，Monge の問題が厳密に解かれたのは独立な結果 (Evans and Gangbo, 1999), (Ambrosio, 2003) まで待つ必要がある．

なお，のちに (Kantorovich, 1948) にて Monge の問題と関連づけているが，Kantorovich ははじめは Monge の議論がすでに存在することを知らなかったという (Vershik, 2013)．

2 Kantorovich の定式化と最適化

2.1 はじめに

最適輸送は数学，特に偏微分方程式論，非線型解析の分野で重要な道具になりつつあるが，その遥かに前から最適化，経済学の分野で活躍を始めた．

特に，Leonid Kantorovich は線型計画法による解決から，ノーベル経済学賞を与えられている．

この章では Kantorovich のオリジナルの理論を離散の場合に見て，次章 3 で一般の確率測度に対して一般化する．

2.2 Kantorovich の問題

\(\mathbb{R}^d\) 上の２つの点群 \(\{x_i\}_{i=1}^n,\{y_j\}_{j=1}^m\subset\mathbb{R}^d\) が重み \(a\in\mathbb{R}^n,b\in\mathbb{R}^m\) 付きで与えられているとする： \[ \sum_{i=1}^na_i=\sum_{j=1}^mb_j=1. \]

\((x,a)\) と付値された資源を \((y,b)\) の状態に運ぶ計画の全体は，\(a,b\) を周辺分布にもつ結合分布の全体として \[ U(a,b):=\left\{P\in M_{n,m}(\mathbb{R})\,\middle|\,P\ge 0,\sum_{j=1}^mP_{ij}=a_i,\sum_{i=1}^nP_{ij}=b_j\right\} \] と表せる．3

この輸送計画のうち，コスト \(C=(c(x_i,x_j))\in M_{n,m}(\mathbb{R})\) に関する輸送コストを最小にする計画を見つける問題を (Kantorovich, 1942) の問題 という： \[ \min_{P\in U(a,b)}(C|P)_\mathrm{HS}=\min_{P\in U(a,b)}\sum_{i=1}^n\sum_{j=1}^mC_{ij}P_{ij}. \]

実はこの問題は，凸制約 \(P\ge0\) の下での，線型目的関数 \((C|P)_\mathrm{HS}\) の最小化問題になっている．

従って，simplex 法などの線型計画法により解くことができる．

2.3 機械学習への応用

特に \(c(x,y)=d(x,y)^p\) と取った場合，最適輸送コスト \[ W_c(a,b) = \min_{P \in U(a,b)}(C|P) \] は点群の間の距離を定める．

このような構成は \(E\) の距離 \(d\) の構造のみに由来するため，Euclid 空間に限らず実行可能である．

すなわち最適輸送の考え方は，コスト \(c\) または損失 \(l\) さえ定義可能であれば，極めて一般の空間上に距離を定義することに使える．

特に距離 \(d\) の性質を考慮した最適輸送距離は，機械学習において自然な損失関数を与える (5.6節 Figalli and Glaudo, 2023), (佐藤竜馬, 2023), (Figalli and Ambrosio, 2024)．

2.4 双対問題

3 一般の最適輸送問題

3.1 はじめに

前節では離散空間の場合を扱った．

一般的には最適輸送問題の解は カップリング によって与えられる．

カップリングとは確率論的な概念であり，「輸送計画」を数学的に表現する格好の概念である．

逆に言えば解の表現に確率論的な発想が必要であった点が，力学や Plateau 問題における曲線や曲面が解となる変分問題とは違い，変分問題の中でも異色なものであると言える．

そこでまずカップリングの概念を定義し，一般の空間上での最適輸送問題を定式化する．

3.2 カップリング

可測空間 \(E\) 上の２つの確率分布 \(\mu,\nu\in\mathcal{P}(E)\) の カップリング または 輸送計画 とは，\(\mu,\nu\) を２つの周辺分布にもつ \(E^2\) 上の Radon 確率測度 \(\pi\in P(E^2)\) をいう．

カップリングの全体を \[ C(\mu,\nu):=\left\{\pi\in P(E^2)\:\middle|\:\substack{(\mathrm{pr}_1)_*\pi=\mu,\\(\mathrm{pr}_2)_*\pi=\nu.}\right\} \] で表す．4

この名前の由来は，次の分解を与える 確率核 \(P\) を考えるとわかる： \[ \pi(dxdy)=\mu(dx)P(x,dy) \]

独立カップリング

\(\pi:=\mu\otimes\nu\) を 独立カップリング (trivial coupling) という．この場合， \[ P(x,dy)=\nu(dy),\qquad x\in E, \] が成り立つ．

独立カップリング \((X,Y)\sim\pi\) について，\(X\) を \(Y\) で条件付けても分布は変わらない．

確定カップリング / Monge カップリング

一方で，ある関数 \(T:E\to E\) が存在して， \[ P(x,dy)=\delta_{T(x)}(dy) \] を満たすカップリングを 確定カップリング (deterministic coupling) または Monge カップリングという．

このとき \(T_*\mu=\nu\) の関係があり，\(T\) は変数変換としても働く．この \(T\) を 輸送写像 (transport map) または Monge 輸送計画という．5

3.3 最適輸送問題

最適輸送問題は２地点間の輸送コストを表す関数 \[ c:E\times E\to\mathbb{R}_+ \] と，開始・終了時点での資源の密度分布 \(\mu,\nu\in\mathcal{P}(E)\) に関して定まるもので，輸送にかかる総コストの最小化を図る．

輸送計画はカップリング \(\kappa\in C(\mu,\nu)\) として定式化でき，このことを用いると Kantorovich の最適輸送問題 は \[ \min_{\kappa\in C(\mu,\nu)}\int_{E\times E}c(x,y)\kappa(dxdy) \] と定式化できる．

3.4 Monge の輸送計画

一方で Monge の最適輸送問題 は，この解を Monge カップリングの中で探す（第 1.5 節）．6

この制約は極めて強く，一般に解が存在するとは限らない．実際 Monge の問題では，一箇所の資源を分割しそれぞれを別の目的地に運ぶことが許されないから，Delta 測度は Delta 測度以外に輸送することが出来ないことになる．7

Kantorovich の最適輸送問題は，極めて一般的な設定で最適カップリング \(\pi\in C(\mu,\nu)\) の存在が保証される．

さらに，\(c\) が \(E\) 上の距離様の関数である場合，最適輸送コストも距離様の性質を満たすため，確率分布の間の距離を構成することができる．

3.5 最適輸送計画

\(d:E\times E\to\mathbb{R}_+\) は距離公理のうち三角不等式のみ満たさない可測関数とする．これを 半距離 とここでは呼ぶ．

定義 (coupling / optimal cost distance)8

半距離 \(d\) が \(\mathcal{P}(E)\) 上に定める カップリング距離 または 最適輸送距離 とは，Monge-Kantorovich 最小化問題 の解 \[ d(\mu,\nu):=\inf_{\kappa\in C(\mu,\nu)}\int_{E^2}d(x,y)\kappa(dxdy) \] をいう．

下界を達成するカップリング \(\kappa\in C(\mu,\nu)\) を \(d\)-最適カップリング または 最適輸送計画 といい，その全体を \(C_\mathrm{opt}(\mu,\nu)\) と表す．

最適輸送計画の存在9

\(E\) が Polish 空間，半距離 \(d\) が下半連続であるとする： \[ d(x,y)\le\liminf_{n\to\infty}d(x_n,y_n). \] このとき，最適輸送計画が存在する：\(C_\mathrm{opt}(\mu,\nu)\ne\emptyset\)．

\(C(\mu,\nu)\subset\mathcal{P}(E^2)\) は一様に緊密である

実際， \(\mu,\nu\in\mathcal{P}(E)\) は緊密であるから，任意の \(\epsilon>0\) に対して，ある \(K_1,K_2\overset{\textrm{cpt}}{\subset}E\) が存在して，

\[ \mu(K_1)\ge1-\frac{\epsilon}{2},\qquad\nu(K_2)\ge1-\frac{\epsilon}{2}. \]

\(K:=K_1\times K_2\) と定めると，任意の \(\kappa\in C(\mu,\nu)\) に対して，Bonferroniの不等式から次が成り立つ：

\[ \kappa(K)=\kappa\biggr((K_1\times K)\cap(K\times K_2)\biggl)\ge1-\epsilon. \]

構成

任意の \(n\in\mathbb{N}^+\) に対して，ある \((\xi_n,\eta_n)\in C(\mu,\nu)\) が存在して，

\[ \operatorname{E}[d(\xi_n,\eta_n)]\le d(\mu,\nu)+\frac{1}{n}. \]

このとき \(\lim_{n\to\infty}\operatorname{E}[d(\xi_n,\eta_n)]=d(\mu,\nu)\) であることに注意． \(C(\mu,\nu)\) は一様に緊密であったから，Prohorovの定理より，ある部分列 \(\{(\xi_{n_k},\eta_{n_k})\}\) が存在して， ある極限 \((\xi,\eta)\) に収束する．このとき，射影 \(\mathrm{pr}_i:E^2\to E\) は連続であることより，各成分も弱収束するから，やはり \((\xi,\eta)\in C(\mu,\nu)\) ． Skorohodの定理から，ある確率変数列 \(\{(\widetilde{\xi}_k,\widetilde{\eta}_k)\}\) と \((\widetilde{\xi},\widetilde{\eta})\) が存在して， \((\widetilde{\xi}_k,\widetilde{\eta}_k)\xrightarrow{\;\text{a.s.}}(\widetilde{\xi},\widetilde{\eta})\) ．

証明の完了

すると \(d\) の下半連続性から，

\[ d(\widetilde{\xi},\widetilde{\eta})\le\liminf_{k\to\infty}d(\widetilde{\xi}_k,\widetilde{\eta}_k). \]

この不等式を，Fatouの補題と併せると，

\[ \operatorname{E}[d(\widetilde{\xi},\widetilde{\eta})]\le\operatorname{E}\left[\liminf_{k\to\infty} d(\widetilde{\xi}_k,\widetilde{\eta}_k)\right]\le\liminf_{k\to\infty}\operatorname{E}[d(\widetilde{\xi}_k,\widetilde{\eta}_k)]=\liminf_{k\to\infty}\operatorname{E}[d(\xi_k,\eta_k)]=d(\mu,\nu). \]

3.6 双対問題

命題 (Kantorovich, 1940)

次の等式が，両辺が有限である限り成り立つ： \[ \min_{\kappa\in C(\mu,\nu)}\int_{E^2}d(x,y)\kappa(dxdy)=\max_{\varphi(x)+\psi(y)+c(x,y)\ge0}\int_E-\phi\,d\mu+\int_Y-\psi\,d\nu. \]

4 最適輸送と数学

4.1 はじめに

連続体力学における連続方程式，多孔質媒体方程式をはじめとして，種々の方程式は密度 \(\rho_t\) に関する微分方程式になっている．

だが，密度とは本質的に確率測度として理解できる．物理的には点群であるような対象は，むしろ確率測度と見た方が直接的である．

１つの方程式を関数方程式と測度方程式の両面で解釈することができるとき，前者を Euler 流，後者を Lagrange 流の解釈ともいう (Villani, 2009, p. 14)．

最適輸送理論の大きな貢献の１つに，従来 Euler 流に解釈されていたものを，Lagrange 流に解釈し直す方法を与えることが挙げられる (Ambrosio and Quarteroni, 2024)．

4.2 連続方程式

連続方程式 / 質量保存の法則10

\(M\) を \(C^1\)-Riemann 多様体，\(F:[0,T)\times M\to TM\) を可測なベクトル場とする．\((\mu_t)_{t\in[0,T]}\subset\mathcal{P}(M)\) を弱連続な曲線で次を満たすとする： \[ \int^T_0\int_M\lvert F_t(x)\rvert\mu_t(dx)\,dt<\infty. \]

このとき，次の２条件は同値：

  1. \((\mu_t)\) は \[ F_t(\phi_t(x))=\frac{d \phi_t}{d t}(x) \] を満たす確率的フロー \((\phi_t)\) の分布である．

  2. \((\mu_t)\) は次の連続方程式の弱解である： \[ \frac{\partial \mu_t}{\partial t}+\operatorname{div}_x(F_t\mu_t)=0. \]

さらにベクトル場 \(F_t\) が局所 Lipschitz 連続であるとき，\((\phi_t)\) はフローを定め， \[ \mu_t=(\phi_t)_*\mu_0 \] が成り立つ．

これは \(\mathcal{P}(M)\) 上の PDE に対する特性曲線法と見ることもできる．11

4.3 Schrödinger 橋問題

Schrödinger 橋問題 (Schrödinger, 1931), (Schrödinger, 1932) は，確率過程の分布の空間 \(\mathcal{P}(C([0,1];\mathbb{R}^d))\) 上の次の変分問題である：

5 文献紹介

Springer Math Podcast では 2023 年に最適輸送に関連する Podcast を３つ発表しており，(Ambrosio and Quarteroni, 2024), (Figalli and Ambrosio, 2024), (Gigli and De Lellis, 2024) はその記事化である．最適輸送について深入りする前に，数学的な背景を知ったり，モチベーションを上げるために格好である．

References

Ambrosio, L. (2003). Lecture notes on optimal transport problems. In Mathematical aspects of evolving interfaces: Lectures given at the c.i.m.-c.i.m.e. Joint euro-summer school held in madeira, funchal, portugal, july 3-9, 2000, pages 1–52. Berlin, Heidelberg: Springer Berlin Heidelberg.
Ambrosio, L., Gigli, N., and Savaré, G. (2008). Gradient Flows: In Metric Spaces and in the Space of Probability Measures. Birkhäuser Basel.
Ambrosio, L., and Quarteroni, A. (2024). Talking about optimal transport. In L. Ambrosio and A. Quarteroni, editors, Conversations on optimal transport, pages 1–19. Cham: Springer Nature Switzerland.
Bernoulli, J. (1696). Poblema novum ad cujus solution em mathematici invitantur. Acta Eruditorum, 1, 269.
Brenier, Y. (1987). Decomposition polaire et réarrangement monotone des champs de vecteurs. Comptes Rendus de l’Académie Des Sciences - Series I - Mathematics, 305(19), 805–808.
Euler, L. (1744). Ethodus inveniendi lineas curvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti. Lausannæ ; Genevæ : Apud Marcum-Michaelem Bousquet & Socios.
Evans, L. C., and Gangbo, W. (1999). Differential equations methods for the monge-kantorovich mass transfer problem,Vol. 137. American Mathematical Society.
Fermat, P. de. (1657). Marin cureau de la chambre, la lumière (chez iacqves d’allin, paris, 1657). Personal Correspondence.
Figalli, A. (2023). An introduction to optimal transport and wasserstein gradient flows.
Figalli, A., and Ambrosio, L. (2024). Optimal transport, fields medals and beyond. In L. Ambrosio and A. Quarteroni, editors, Conversations on optimal transport, pages 21–38. Cham: Springer Nature Switzerland.
Figalli, A., and Glaudo, F. (2023). An Invitation to Optimal Transport, Wasserstein Distances, and Gradient Flows. European Mathematical Society.
Gigli, N., and De Lellis, C. (2024). From moving masses to bending spaces: An excursion in metric geometry. In L. Ambrosio and A. Quarteroni, editors, Conversations on optimal transport, pages 39–58. Cham: Springer Nature Switzerland.
Goldstine, H. H. (1980). A history of the calculus of variations from the 17th through the 19th century,Vol. 5. Springer New York.
Hamilton, W. R. (1834). On a general method in dynamics; by which the study of the motions of all free systems of attracting or repelling points is reduced to the search and differentiation of one central relation, or characteristic function. Philosophical Transactions of the Royal Society, 124, 247–308.
Hanc, J. (2017). The original euler’s calculus-of-variations method: Key to lagrangian mechanics for beginners.
Kantorovich, L. V. (1940). On an effective method of solving certain classes of extremal problems. Doklady Akademii Nauk SSSR, 28, 212–215.
Kantorovich, L. V. (1942). On the translocation of masses. Doklady Akademii Nauk SSSR, 37(7-8), 227–229.
Kantorovich, L. V. (1948). On a problem of monge. Uspekhi Matematicheskikh Nauk, 3(2), 225–226.
Kolmogorov, A. N. (1933). Grundegriffe der wahrscheinlichkeitsrechnung,Vol. 2. Springer Berlin, Heidelberg.
Kulik, A. (2018). Ergodic behavior of markov processes: With applications to limit theorems,Vol. 67. De Gruyter: Berlin, Boston.
Lagrange, J.-L. (1788). Mécanique analytique.
Levi, M. (2014). Quick! Find a solution to the brachistochrone problem. In SIAM news. SIAM.
Monge, G. (1781). Mémoire sur la théorie des déblais et des remblais. Imprimerie Royale.
Schrödinger, E. (1931). Über die umkehrung der naturgesetze. Sitzungsberichte Der Preussischen Akademie Der Wissenschaften, Physikalische Mathematische Klasse, 8(9), 144–153.
Schrödinger, E. (1932). Sur la théorie relativiste de l’électron et l’interprétation de la mécanique quantique. Annales de l’institut Henri Poincaré, 2(4), 269–310.
Vershik, A. M. (2013). Long history of the monge-kantorovich transportation problem. The Mathematical Intelligencer, 35(4), 1–9.
Villani, C. (2009). Optimal Transport: Old and New,Vol. 338. Springer Berlin, Heidelberg.
中根美知代. (2000). 物理学から数学へ : Hamilton-jacobi 理論の誕生 (数学史の研究). In 数理解析研究所講究録,Vol. 1130, pages 58–71.
佐藤竜馬. (2023). 最適輸送の理論とアルゴリズム. 講談社サイエンティフィック.

Footnotes

  1. ホロノミック拘束系などでは．↩︎

  2. 3blue1brown の YouTube 動画 も参照．↩︎

  3. 輸送多面体 (transportation polytope) という．コスト行列 \(C\) との衝突を防ぐため，ここでは \(U(a,b)\) と表した．↩︎

  4. Notation の稿も参照．↩︎

  5. (Villani, 2009, p. 6), (Def. 1.4.1 Figalli and Glaudo, 2023) も参照．↩︎

  6. (Figalli, 2023, p. 3), (Figalli and Glaudo, 2023) に従った．↩︎

  7. しかし，任意の連続分布の間には輸送写像が存在する． (Figalli and Glaudo, 2023, p. 9)．↩︎

  8. (Kulik, 2018, p. 122), (Villani, 2009, p. 10) も参照．↩︎

  9. (Kulik, 2018, p. 124) 命題4.3.3，(Villani, 2009, p. 10) も参照．↩︎

  10. (Ambrosio et al., 2008, p. 183) 定理8.3.1 は (Villani, 2009, p. 14) にも取り上げられている．↩︎

  11. (Villani, 2009, p. 19) Bibliographical notes も参照．↩︎