Stan 入門

Bayesian
Computation
Stan
Author

司馬博文

Published

5/17/2024

Modified

9/17/2024

概要
Stan は MCMC や変分推論などのベイズ推論エンジンを備えた，統計モデリングのための確率的プログラミング言語です．CLI，Python，Julia，R など，主要な言語からパッケージを通じて利用可能です．本稿では Stan 言語の基本をまとめます．

リンク集

GitHub, Documentation, Reference Manual．

1 Stan 言語の基本文法

1.1 はじめに

Stan 言語は確率モデルを３つのブロックに分けて記述する．その３つとはデータ，パラメータとモデルである．

以上の３要素により，事後分布が定まる．それぞれの要素は，対応した名前を持ったスコープ {} 内で，この順番で定義される慣習がある．

以前のスコープ内で定義された識別子は，その後のスコープでも利用可能になる．

stan_code.stan
data {
    int<lower=0> N;  // N >= 0
    array[N] int<lower=0, upper=1> y;  // y[n] in {0, 1}
}
parameters {
    real<lower=0, upper=1> theta;  // theta in [0, 1]
}
model {
    theta ~ beta(1, 1);  // uniform prior
    y ~ bernoulli(theta);  // observation model
}

その後 Stan プログラムは事後分布の対数密度を表す C++ 関数にコンパイルされる．

最終的にこの対数尤度を用いて，その勾配を自動微分により計算し，Hamiltonian Monte Carlo による事後分布サンプリングを実行する．

Stan エコシステムの詳説は次節 2 に回し，ここでは Stan 言語の基本に集中する．

1.2 確率的プログラミング言語

Stan 言語のように確率モデルを記述する（より正確には事後分布の尤度を記述する高級）言語を 確率的プログラミング言語 (PPL: Probabilistic Programming Language) という．

最初期の確率的プログラミング言語の１つに WinBUGS (Lunn et al., 2000) の実装に代表される BUGS (Bayesian analysis Using Gibbs Sampling) がある．

BUGS では事後分布を詳細に 有向グラフィカルモデル (DAG) で記述し，Gibbs Sampling により事後分布をサンプリングするという仕組みであった．

Stan 言語はさらに柔軟に，（正規化されているとは限らない）対数尤度を記述できるようになっている．

理想的にはあらゆる確率モデルを扱いたいものであるが，現状の Stan 言語はパラメータとしては連続変数のみを持つモデルのみが定義可能である．

1.3 data ブロック

Stan は静的な型システムを持ち，変数宣言の際には必ず型を指定する必要がある．

Stan の代表的なデータ型

  • 実数 \(x\in\mathbb{R}\)

    real x;

  • 実数 \(x\in[a,b]\)

    real<lower=a upper=b> x;

  • 単体 \(x\in[0,1]^N,\sum_{n=1}^Nx_n=1\)

    simplex[N] x;

  • 自然数 \(N\in\mathbb{N}\)

    int<lower=0> N;

  • 配列 \(x\in\mathbb{R}^N\)：純粋なコンテナ型であり，線型代数ライブラリは適用不可．

    array[N] real x;

    real x[N] という記法は Stan 2.26 以降使われないことに注意（docs 参照）．

なお，各ブロック内において，あらゆる変数宣言は全ての非宣言的文の前に来る必要がある．

{
    real variable1 = 5;
    variable1 /= 2;  // ここでエラー
    real variable2 = exp(variable1);
}

1.4 transformed data ブロック

data ブロックでは許されないが，一般に Stan 言語では変数宣言と同時に代入もできる．

代入を省略した場合は NaN によって初期化される．

Stan の代表的な線型代数関連のデータ型

  • ベクトル \(x\in\mathbb{R}^5\)：c++ の線型代数ライブラリが使える

    vector[5] x = [0, 1, 2, 3, 4];

  • 横ベクトル \(y\in(\mathbb{R}^5)^*\)：\(y*x\) が計算可能．

    row_vector[5] y = [1, 2, 3, 4, 5]';
x*y; // 計算可能

  • 行列 \(A\in M_{N,M}(\mathbb{R})\)

    matrix[N, M] A;

transformed data ブロックでは，観測される訳でもなければパラメータでもないような，内部で使われる変数が定義される．

1.5 parameters ブロック

parameters ブロックも同様にして変数を宣言する．

model ブロックで使われる変数は，data, parameters ブロックのいずれかで宣言されている必要がある．

\(x\in[a,b]^N\) のような制約領域を持つ変数が parameters ブロックで宣言された場合，Stan は内部でパラメータ変換を行い，\([a,b]\) を \(\mathbb{R}\) 上に写してサンプリングを実行する．

Gamma 分布のように台が \(\mathbb{R}\) の部分集合になるような事前分布を扱う場合，対応する制約領域をパラメータに定義することがサンプリングの効率を上げる．

一方で，\(\mathbb{R}\) 全体を台に持つ事前分布を持つパラメータに対して制約領域を宣言した場合，truncate をした事前分布を定義したことに等価になる．

1.6 model ブロック

モデルブロックでは対数密度関数の値が変数 target として保持されており，target() 関数でアクセス可能である．

次の３つの文は等価になる：

beta ~ normal(0, 1);
beta ~ normal(beta | 0, 1);  // syntax sugar
target += normal_lpdf(beta | 0, 1);  // 実際の処理に近い

1.7 ループと制御

for (n in N1:N2) {
  // Statements executed for each N1 <= n <= N2
}

if (condition) {
  // Statements evaluated if condition is true
} else {
  // Statements evaluated if condition is false
}

1.8 transformed parameters / Generated Quantities ブロック

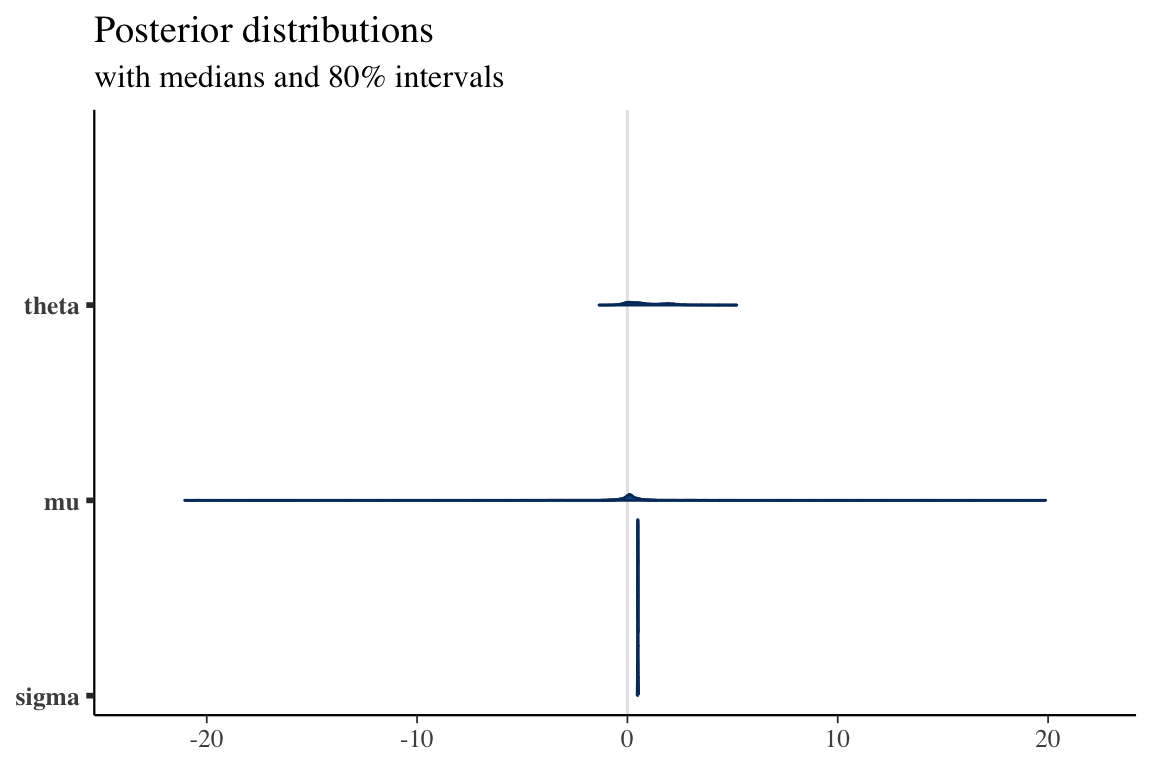
transformed parameters ブロックと Generated Quantities ブロックでは，parameters ブロックで宣言されたパラメータの関数として推定対象を定義する．

この推定対象は推論後に事後平均が取られて報告される．

２つの違いは，transformed parameters ブロックでは model ブロックの前に配置され，model ブロックでも使えるのに対し，Generated Quantities ブロックでは model ブロックの後に配置され，純粋に事後分布の関数として処理される点である．

なお，関数定義は functions ブロックで行う．

functions {
    real baseline(real a1, real a2, real theta) {
        return a1 * theta + a2;
    }
}

2 Stan エコシステムの概観

2.1 Stan の推論エンジン

Stan の推論エンジンとして，HMC の他に２つの C++ アルゴリズムが用意されており，それぞれ BFGS 法による点推定と変分推定を実装している．

2.2 Stan 数学ライブラリ

Stan 言語により定義された確率モデル（対数密度関数）が実際に評価可能にするための C++ 関数のライブラリである．

使える関数のリストは Stan Functions Reference を参照．

基本的な数学的関数や統計的関数に加えて，自動微分が実装されており，対数密度関数の勾配や Hessian も計算可能である．

2.3 Stan インターフェイス

2.3.1 CmdStan の仕組み

CmdStan は makefiles の集合からなる最も軽量な，コマンドラインベースのインターフェイスである．

これを直接 R で wrap した CmdStanR パッケージ や CmdStanPy パッケージが存在し，同時に Julia Stan.jl, Mathematica MathematicaStan, Matlab MatlabStan, Stata StataStan からも利用可能である．

Stan の Math ライブラリ，Algorithm ライブラリなどの出力をテキストファイルで出力してやり取りする．

CmdStan は最も軽量なインターフェイスであり，Stan の性能を純粋に引き出す場合に使われる．

2.3.2 CmdStan のインストール

CmdStan Installation によると，conda による方法とソースからのインストールの2つの方法がある．

一方で次稿で扱う CmdStanR を通じてインストールすることもできる：

2.3.3 RStan と PyStan

R と Python という２大言語を Stan と直接繋げるインターフェイスを提供している．

CmdStan のように一度テキストファイルに書き出すということがなく，メモリ上でやり取りされるが，それ故に CmdStan よりも追加の処理が多くなりがちである．

3 文献紹介

手軽に概要を掴むには Michael Betancourt によるブログ記事 An introduction to Stan が良い．

より本格的な解説論文には (Gelman et al., 2015), (Carpenter et al., 2017) がある．

公式の文献紹介 が stan.org から出ているが，情報が古い．

また，Stan には 日本語のマニュアル もある：stan-ja (GitHub)．

References

Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., … Riddell, A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1), 1–32.
Gelman, A., Lee, D., and Guo, J. (2015). Stan: A probabilistic programming language for bayesian inference and optimization. Journal of Educational and Behavioral Statistics, 40(5), 530–543.
Lunn, D. J., Thomas, A., Best, N., and Spiegelhalter, D. (2000). WinBUGS - a bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing, 10(4), 325–337.