R 上の Stan インターフェイス

RStan と CmdStanR

Bayesian
Computation
Stan
R
Author

司馬 博文

Published

9/19/2024

Modified

9/19/2024

概要
Stan は MCMC や変分推論などのベイズ推論エンジンを備えた，統計モデリングのための確率的プログラミング言語です．CLI，Python，Julia，R など，主要な言語からパッケージを通じて利用可能ですが，本稿では特に R からの利用方法をまとめます．

概観

RStan は Rcpp や inline といったパッケージにより C++ を R から呼び出すことで，Stan とのインターフェイスを実現している．

一方で CmdStanR は CmdStan という Stan のコマンドラインインターフェイスを R から呼び出すことで，Stan とのインターフェイスを実現している．

1 RStan パッケージ

1.1 はじめるために

RStan Getting Started に従って実行します．

1.1.1 インストール

packageVersion("rstan")

を実行してすでに存在する場合は，次を実行します

remove.packages("rstan")
if (file.exists(".RData")) file.remove(".RData")

ほとんどの場合，次の１行でインストールできます：

install.packages("rstan", repos = "https://cloud.r-project.org/", dependencies = TRUE)

1.1.2 RStan の利用のためには，c++ コンパイラが必要

XCode コマンドラインツールをインストールすることにより，/Library/Developer/CommandLineTools/usr/bin に clang++ がインストールされます．

clang++ -v -E -x c++ /dev/null

現在では，macrtools を通じて C++ コンパイラを R 内でインストールすることもできます．

RStan Getting Started の Configuring C Toolchain for Mac では，次のようなコンパイラの最適化が推奨されています：

dotR <- file.path(Sys.getenv("HOME"), ".R")
if (!file.exists(dotR)) dir.create(dotR)
M <- file.path(dotR, "Makevars")
if (!file.exists(M)) file.create(M)
arch <- ifelse(R.version$arch == "aarch64", "arm64", "x86_64")
cat(paste("\nCXX17FLAGS += -O3 -mtune=native -arch", arch, "-ftemplate-depth-256"),
    file = M, sep = "\n", append = FALSE)

これにより ~/.R/Makevars に次のような行が追加されます：

CXX17FLAGS += -O3 -mtune=native -arch arm64 -ftemplate-depth-256

1.1.3 検証

次のコードが実行されれば，インストールは成功しています．

example(stan_model, package = "rstan", run.dontrun = TRUE)

1.2 stan 関数

RStan パッケージの本体は stan 関数である：

stan(file, model_name = "anon_model", model_code = "", fit = NA,
  data = list(), pars = NA,
  chains = 4, iter = 2000, warmup = floor(iter/2), thin = 1,
  init = "random", seed = sample.int(.Machine$integer.max, 1),
  algorithm = c("NUTS", "HMC", "Fixed_param"),
  control = NULL, sample_file = NULL, diagnostic_file = NULL,
  save_dso = TRUE, verbose = FALSE, include = TRUE,
  cores = getOption("mc.cores", 1L),
  open_progress = interactive() && !isatty(stdout()) &&
                  !identical(Sys.getenv("RSTUDIO"), "1"),
  ...,
  boost_lib = NULL, eigen_lib = NULL
  )

1.2.1 モデルの受け渡し

model_code="" が Stan モデルを定義するコードを，文字列として直接受け渡すための引数である．

返り値はフィット済みの stanfit オブジェクトである．

他の方法は次のとおり：

  • file としてファイルへのパスを渡す
  • フィット済みの stanfit オブジェクトを fit 引数として渡す

1.2.2 重要な引数

  • data：データを与える．list 型．
  • iter：繰り返し回数．デフォルトは 2000．
  • chains：チェイン数．デフォルトは 4．

1.2.3 stanfit オブジェクト

stan 関数は Stan モデルを C++ に変換して実行し，結果を stanfit オブジェクトとして返す．

これに対して print, summary, plot などのメソッドが利用可能である．

さらに，次の様にして MCMC サンプルを取り出すことができる：

  • as.array メソッドを用いて MCMC サンプルを array 型で取り出す
  • extract メソッドを用いて MCMC サンプルを list 型で取り出す
  • posterior ライブラリの as_draws_df メソッドを用いて MCMC サンプルを df 型で取り出す．種々のデータ型 <format> に対して as_draws_<format> が存在する．

取り出した MCMC サンプルは bayesplot パッケージの mcmc_trace, mcmc_dens などの関数を用いて可視化することができる．

1.2.4 例１：軌道と事後分布の可視化

scode <- "
parameters {
  array[2] real y;
}
model {
  y[1] ~ normal(0, 1);
  y[2] ~ double_exponential(0, 2);
}
"
fit <- stan(model_code = scode, iter = 10000, chains = 4, verbose = FALSE)
library(bayesplot)

mcmc_trace(as.array(fit), pars = c("y[1]", "y[2]"))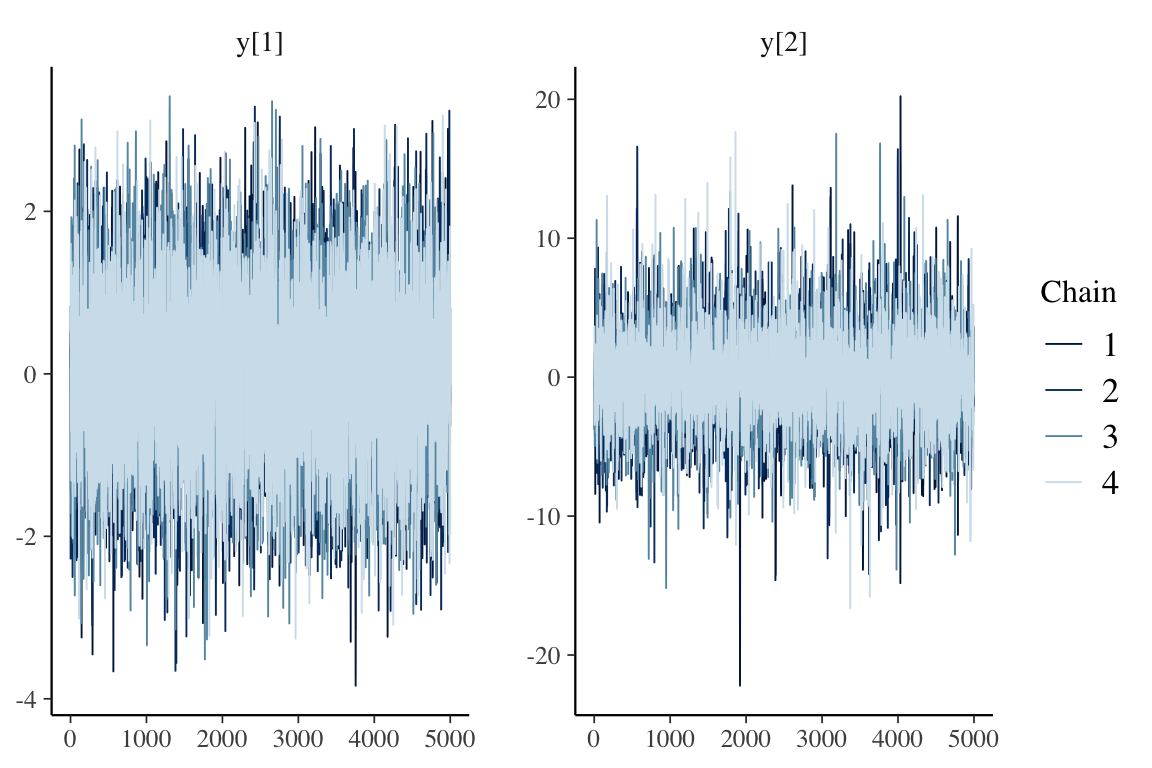

軌道のプロット
mcmc_dens(as.array(fit), pars = c("y[1]", "y[2]"))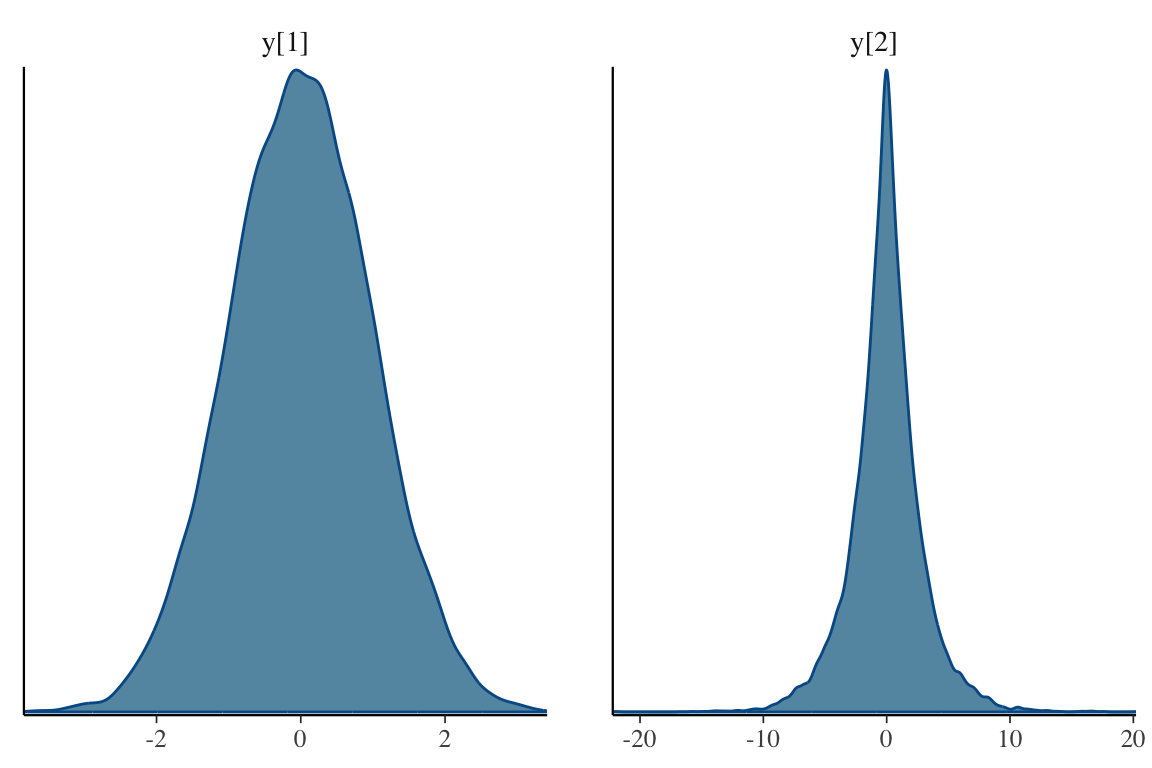

密度のプロット

1.2.5 例２：確率過程の統計推測

OU 過程

\[ dX_t=\theta(\mu-X_t)\,dt+\sigma\,dW_t \]

に対して，stan 関数でベイズ推定を実行してみます．

library(yuima)
model <- setModel(drift = "theta*(mu-X)", diffusion = "sigma", state.variable = "X")

パラメータは \[ \begin{pmatrix}\theta\\\mu\\\sigma\end{pmatrix} = \begin{pmatrix}1\\0\\0.5\end{pmatrix} \tag{1}\] として YUIMA を用いてシミュレーションをし，そのデータを与えてパラメータが復元できるかをみます．

library(rstan)
excode <- "data {
            int N;
            real x[N+1];
            real h;
          }

          parameters {
            real theta;
            real mu;
            real<lower=0> sigma;
          }

          model {
            x[1] ~ normal(0,1);
            for(n in 2:(N+1)){
              x[n] ~ normal(x[n-1] + theta * (mu - x[n-1]) * h,  sqrt(h) * sigma);
            }
          }"

sampling <- setSampling(Initial = 0, Terminal = 3, n = 1000)
yuima <- setYuima(model = model, sampling = sampling)
simulation <- simulate(yuima, true.parameter = c(theta = 1, mu = 0, sigma = 0.5), xinit = rnorm(1))
sde_dat <- list(N =  yuima@sampling@n,
                  x = as.numeric(simulation@data@original.data),
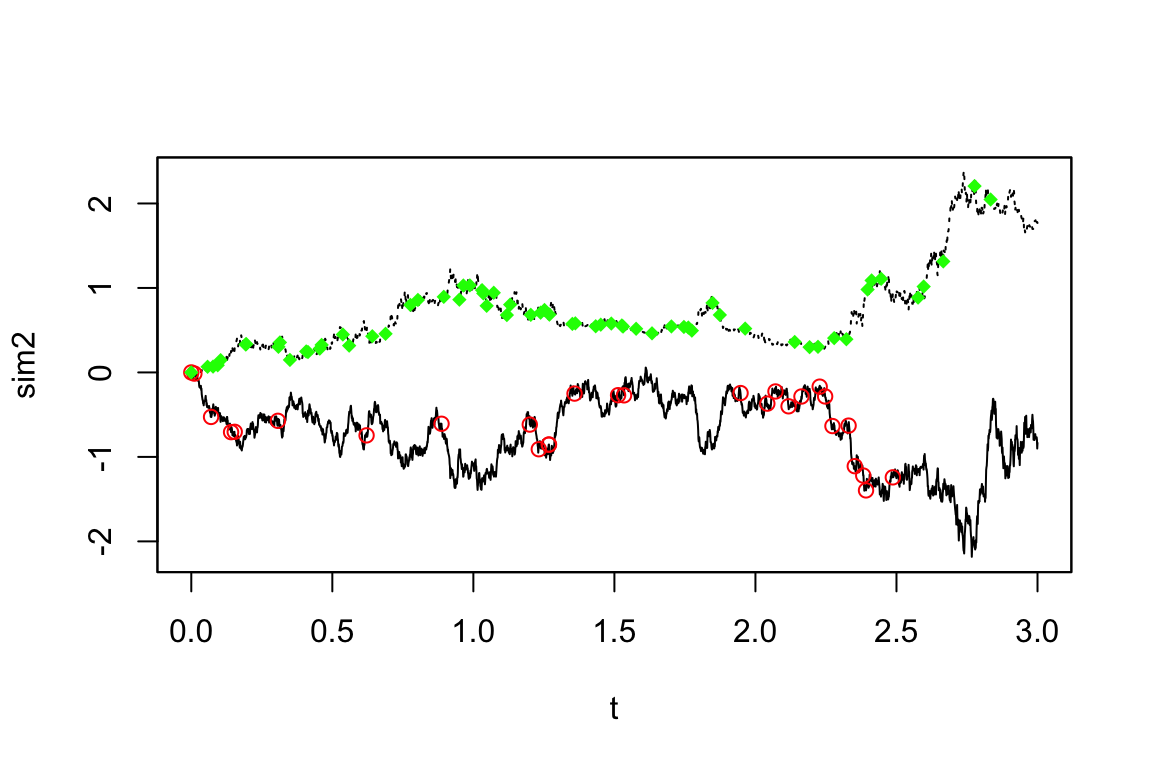
                  h=yuima@sampling@Terminal/yuima@sampling@n)
# シミュレーション結果
plot(simulation)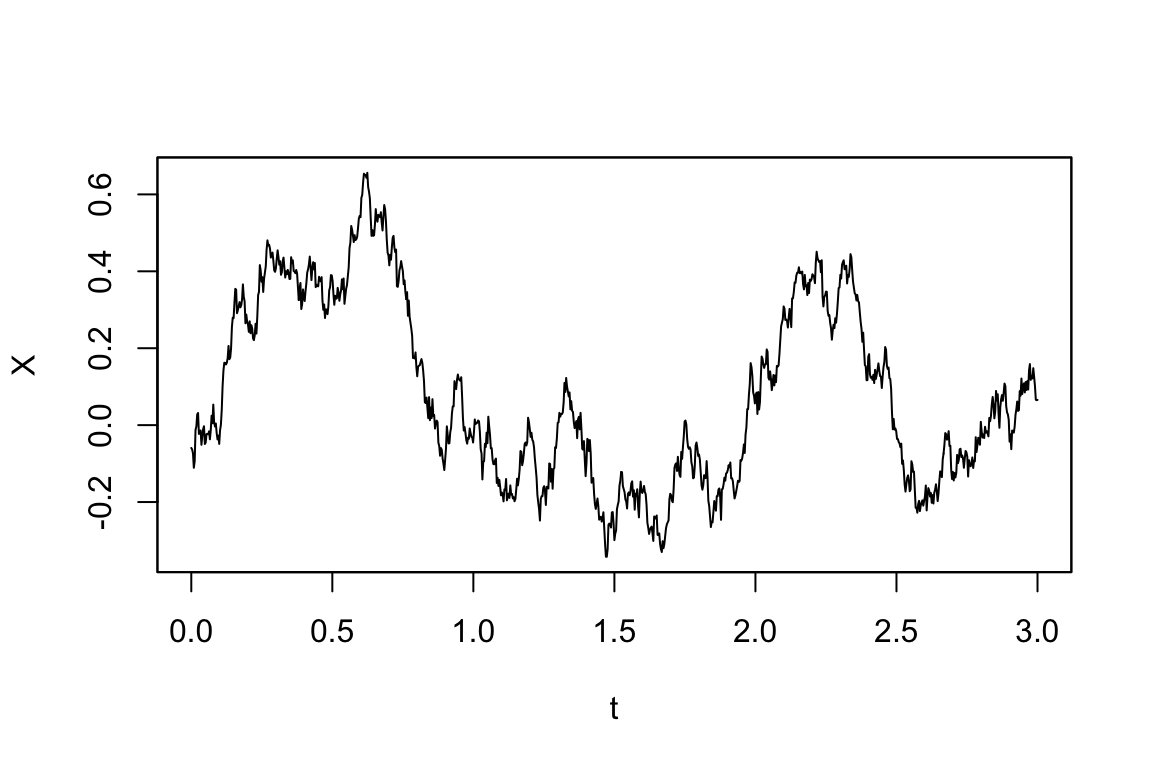

# ベイズ推定
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

fit <- stan(model_code=excode, data = sde_dat, iter = 1000, chains = 4)
print(fit)
Inference for Stan model: anon_model.
4 chains, each with iter=1000; warmup=500; thin=1; 
post-warmup draws per chain=500, total post-warmup draws=2000.

         mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
theta    0.89    0.25 1.01   -0.44    0.07    0.59    1.70    3.27    17 1.14
mu       0.02    0.27 3.59   -5.90   -0.15    0.12    0.42    7.23   178 1.02
sigma    0.50    0.00 0.01    0.48    0.49    0.50    0.51    0.52   108 1.07
lp__  3105.37    0.14 1.23 3102.48 3104.76 3105.46 3106.29 3107.15    80 1.06

Samples were drawn using NUTS(diag_e) at Thu Sep 19 16:46:14 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
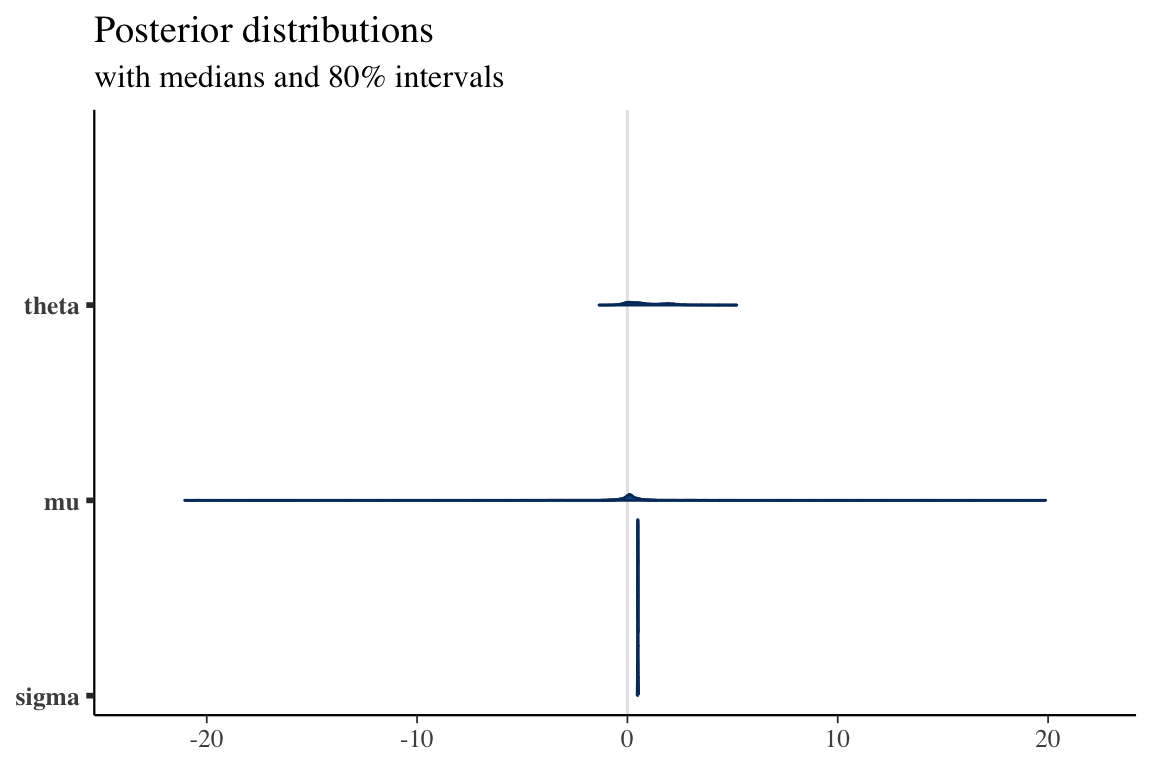
convergence, Rhat=1).

パラメータ (1) がよく推定できていることがわかる．特に \(\sigma\) が安定して推定できている：

plot(fit)
ci_level: 0.8 (80% intervals)
outer_level: 0.95 (95% intervals)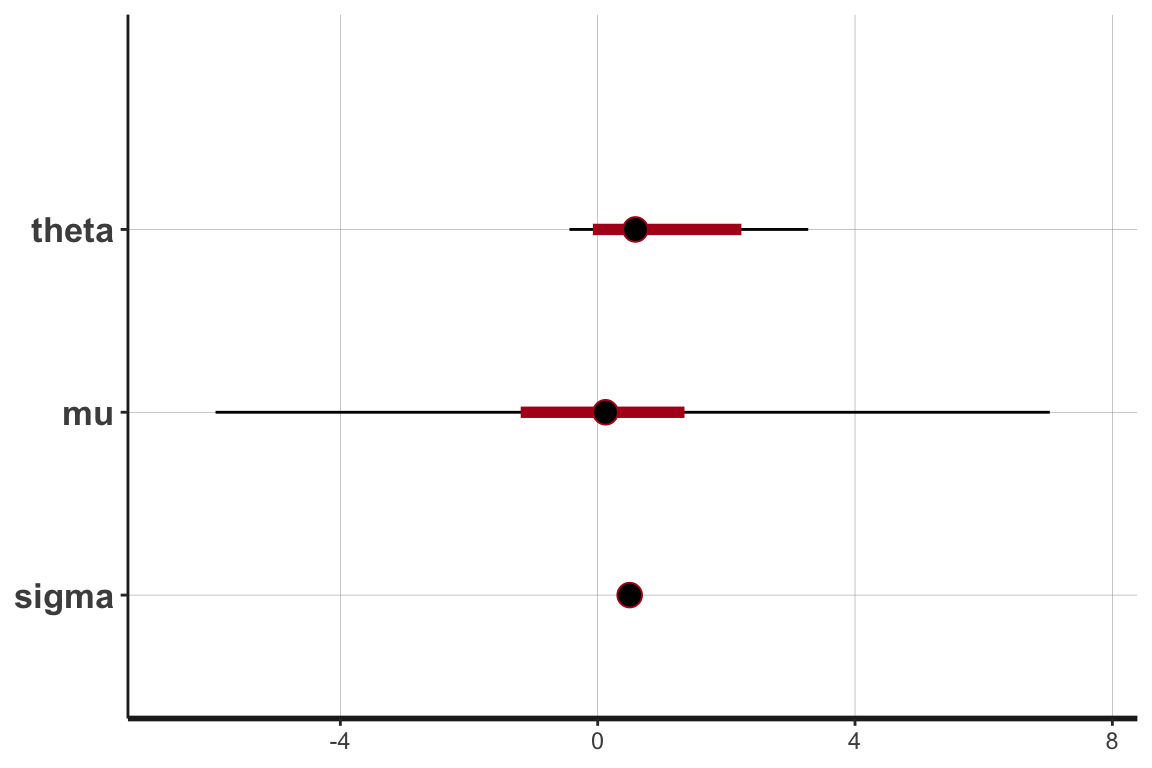

library("bayesplot")
library("rstanarm")
library("ggplot2")

posterior <- as.matrix(fit)
plot_title <- ggtitle("Posterior distributions",
                      "with medians and 80% intervals")
mcmc_areas(posterior,
           pars = c("theta", "mu", "sigma"),
           prob = 0.8) + plot_title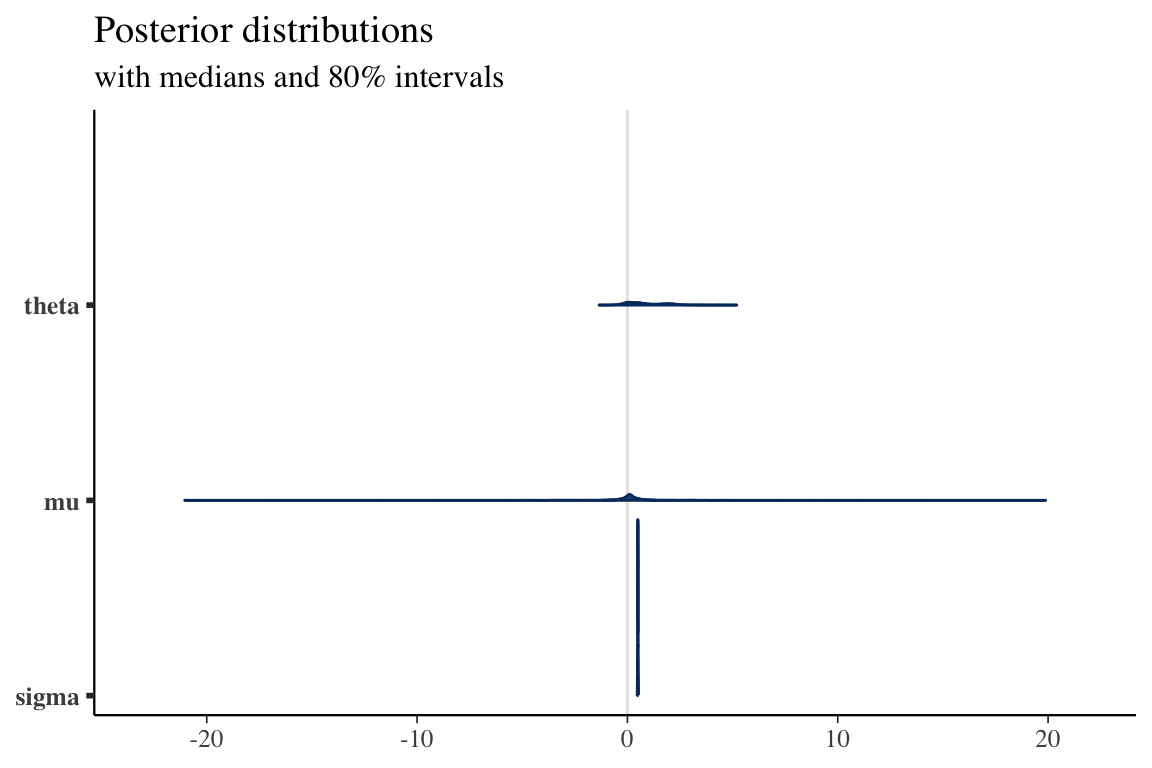

1.3 トラブルシューティング

1.3.1 cmath が見つからない

Quitting from lines 329-343 (adastan.qmd) 

 compileCode(f, code, language = language, verbose = verbose) でエラー: 
  using C++ compiler: ‘Apple clang version 16.0.0 (clang-1600.0.26.3)’using C++17using SDK: ‘MacOSX15.0.sdk’In file included from <built-in>:1:In file included from /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library/StanHeaders/include/stan/math/prim/fun/Eigen.hpp:22:In file included from /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library/RcppEigen/include/Eigen/Dense:1:In file included from /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library/RcppEigen/include/Eigen/Core:19:/Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library/RcppEigen/include/Eigen/src/Core/util/Macros.h:679:10: fatal error: 'cmath' file not found  679 | #include <cmath>      |          ^~~~~~~1 error generated.make: *** [file2546221168fc.o] Error 1
 呼び出し:  .main ... cxxfunctionplus -> <Anonymous> -> cxxfunction -> compileCode
 追加情報:  警告メッセージ: 
1:  パッケージ 'rstan' はバージョン 4.3.1 の R の下で造られました  
2:  パッケージ 'bayesplot' はバージョン 4.3.1 の R の下で造られました  
3:  パッケージ 'rstanarm' はバージョン 4.3.1 の R の下で造られました  


Quitting from lines 329-343 (adastan.qmd) 
 sink(type = "output") でエラー:  コネクションが不正です 
 呼び出し:  .main ... eval -> stan -> stan_model -> cxxfunctionplus -> sink
 実行が停止されました

大変長く書いてあるが，要は fatal error: 'cmath' file not found である．

筆者の場合は純粋な clang++ の問題であった：

❯ echo '#include <cmath>
#include <iostream>

int main() {
    double result = std::sqrt(16.0);
    std::cout << "The square root of 16 is " << result << std::endl;
    return 0;
}' > test.cpp


~
❯ clang++ -std=c++17 test.cpp -o test

test.cpp:1:10: fatal error: 'cmath' file not found
    1 | #include <cmath>
      |          ^~~~~~~
1 error generated.

このような場合は，まず Xcode の再インストールをすると良い．

softwareupdate --list

の出力を用いて，次のようにする：

softwareupdate -i "Command Line Tools (macOS High Sierra version 10.13) for Xcode-10.1"

または次のようにする：

sudo rm -rf /Library/Developer/CommandLineTools
xcode-select --install

2 CmdStanR パッケージ

CmdStanPy, CmdStanR はいずれも Stan のインターフェースである．

CmdStanR は R6 オブジェクトを用いており，大変現代的な実装を持っている．

2.1 はじめるために

Getting Started with CmdStanR に従って実行します．

2.1.1 インストール

install.packages("cmdstanr", repos = c('https://stan-dev.r-universe.dev', getOption("repos")))

2.1.2 CmdStanR の利用のためには，CmdStan が必要

CmdStanR を直接インストールすることもできますが，CmdStanR 内部からインストールすることもできます．

install_cmdstan(cores = 2)
cmdstan_version()
[1] "2.35.0"

多くの場合，自動で CMDSTAN 環境変数にパスが設定されます．次のいずれかの方法で確認できます：

Sys.getenv("CMDSTAN")
cmdstan_path()

CmdStanR の美点の一つは，install_cmdstan() により CmdStan をアップデートすることで最新の Stan を R から簡単に利用できることである．

一方で RStan はパッケージ自体のアップデートを待つ必要がある．

2.2 モデル定義

cmdstan_model() 関数は，Stan 言語による記述されたモデル定義を，C++ コードにコンパイルし，その結果を R6 オブジェクトとして返す．1

cmdstan_model(stan_file = NULL, exe_file = NULL, compile = TRUE, ...)

返り値は CmdStanModel オブジェクトである．ただし R6 オブジェクトでもあり，R6 流のメソッドの呼び方 $ が使える．

file <- file.path(cmdstan_path(), "examples", "bernoulli", "bernoulli.stan")
mod <- cmdstan_model(file)

Stan 言語による定義は次のようにして確認できる：

mod$print()
data {
  int<lower=0> N;
  array[N] int<lower=0, upper=1> y;
}
parameters {
  real<lower=0, upper=1> theta;
}
model {
  theta ~ beta(1, 1); // uniform prior on interval 0,1
  y ~ bernoulli(theta);
}
names(mod$variables())
[1] "parameters"             "included_files"         "data"                  
[4] "transformed_parameters" "generated_quantities"  
names(mod$variables()$transformed_parameters)
character(0)

元となったファイルのパスも stan_file(), exe_file() で確認できる．

2.3 Stan コードの操作

write_stan_file() 関数は Stan コードをファイルに書き出すことができる：

write_stan_file(
  code,
  dir = getOption("cmdstanr_write_stan_file_dir", tempdir()),
  basename = NULL,
  force_overwrite = FALSE,
  hash_salt = ""
)

グローバル環境変数が設定されていない限り，tempdir() で一時ファイルが作成される．これは R セッションの終了とともに削除される．

stan_file_variables <- write_stan_file("
data {
  int<lower=1> J;
  vector<lower=0>[J] sigma;
  vector[J] y;
}
parameters {
  real mu;
  real<lower=0> tau;
  vector[J] theta_raw;
}
transformed parameters {
  vector[J] theta = mu + tau * theta_raw;
}
model {
  target += normal_lpdf(tau | 0, 10);
  target += normal_lpdf(mu | 0, 10);
  target += normal_lpdf(theta_raw | 0, 1);
  target += normal_lpdf(y | theta, sigma);
}
")
mod_v <- cmdstan_model(stan_file_variables)
variables <- mod_v$variables()

2.4 サンプリング

data_list <- list(N = 10, y = c(0,1,0,0,0,0,0,0,0,1))

fit <- mod$sample(
  data = data_list,
  seed = 123,
  chains = 4,
  parallel_chains = 4,
  refresh = 1000 # print update every 1000 iters
)
Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 1 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 1 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 2 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 2 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 2 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 3 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 3 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 3 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 4 Iteration:    1 / 2000 [  0%]  (Warmup) 
Chain 4 Iteration: 1000 / 2000 [ 50%]  (Warmup) 
Chain 4 Iteration: 1001 / 2000 [ 50%]  (Sampling) 
Chain 4 Iteration: 2000 / 2000 [100%]  (Sampling) 
Chain 1 finished in 0.0 seconds.
Chain 2 finished in 0.0 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.2 seconds.

返り値 fit は CmdStanMCMC オブジェクトであり，summary() などのメソッドが使用可能である．

summary() メソッドは，posterior パッケージのメソッド summarise_draws() を自動で使うようになっている．

fit$summary()
# A tibble: 2 × 10
  variable   mean median    sd   mad      q5    q95  rhat ess_bulk ess_tail
  <chr>     <dbl>  <dbl> <dbl> <dbl>   <dbl>  <dbl> <dbl>    <dbl>    <dbl>
1 lp__     -7.30  -7.00  0.797 0.345 -8.86   -6.75   1.00    1923.    2017.
2 theta     0.257  0.241 0.124 0.127  0.0800  0.485  1.00    1232.    1477.
fit$summary(variables = c("theta", "lp__"), "mean", "sd")
# A tibble: 2 × 3
  variable   mean    sd
  <chr>     <dbl> <dbl>
1 theta     0.257 0.124
2 lp__     -7.30  0.797

同様にして draws() メソッドで bayesplot パッケージが呼び出される．

mcmc_hist(fit$draws("theta"))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.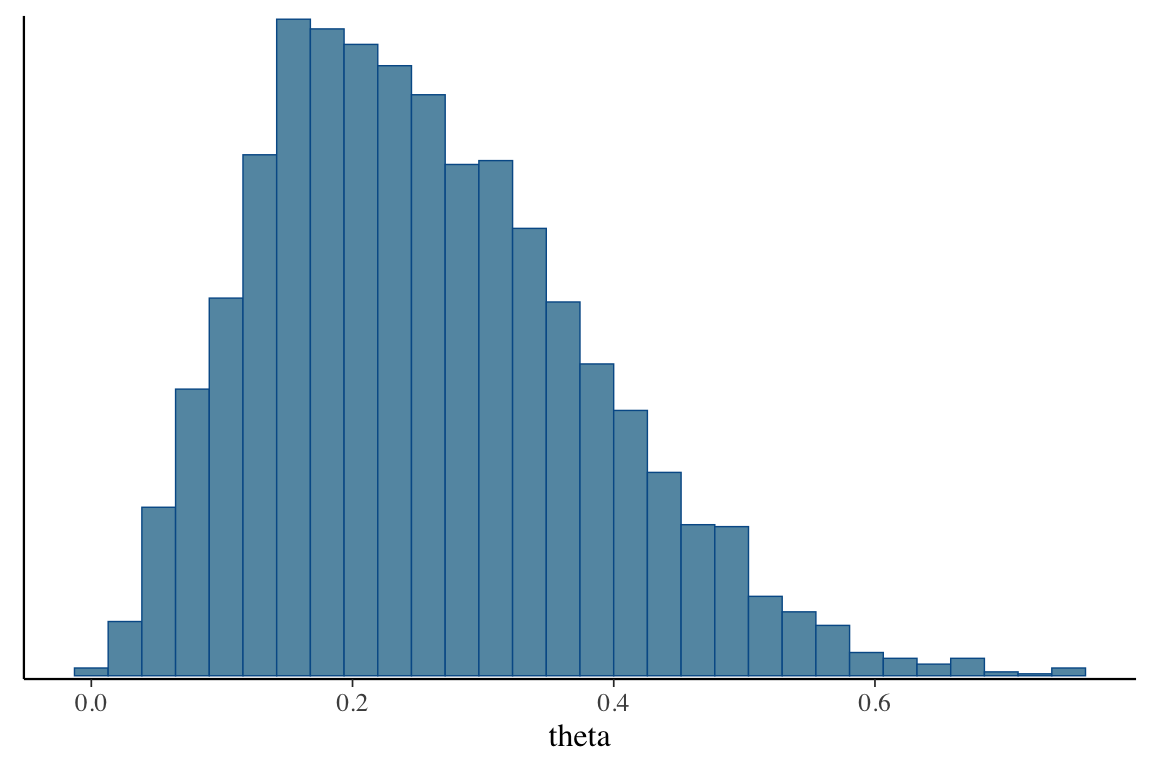

3 文献紹介

Footnotes

  1. 実際には，最初に CmdStanModel オブジェクトを生成し，compile() メソッドを呼び出している．これが compile = TRUE フラッグの存在意義である．↩︎