計算とは何か
計算とサンプリングのはざまにある Monte Carlo 法
1 サンプリングとは何か？
1.1 はじめに
計算機の登場が人類にもたらしたものは，計算手 (computer) を代替する圧倒的計算資源だけではない．
1946 年に Los Alamos でお披露目された最初期の計算機 ENIAC の登場により，科学者たちは「一様乱数をシミュレーションする力」を手に入れた．
この力は何を意味するだろうか？
直ちにこの「力」の破壊的威力を理解したのは Stanislaw Ulam とその話を聴いた John von Neumann であったという．1
その後，この「力」は Monte Carlo 法の名前を得て，(Nicholas Metropolis and Ulam, 1949) では Boltzmann 方程式や Schrödinger 方程式をシミュレーションすることに応用され，最終的に Los Alamos での研究成果は原爆として結実した．
この衝撃的な登場をした「力」は，その後平和が訪れた世界において，どのように使われているのであろうか？
本章では，Monte Carlo 法はその枠にとどまらず，「生成」「シミュレーション」「サンプリング」など種々の名前で，現代の生活を下支えしていると論じる．
1.2 「生成」としてのサンプリング
GAN，VAE，正規化流，拡散模型 などは，いずれも潜在変数モデルを学習していることに等しい．
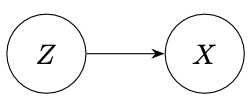
数学的には \(Z\to X\) とは 確率核 であり，Markov 圏 における射とも見れる．
1.2.1 階層モデルに内包される概念の総体について
欠測データモデル，潜在変数モデルは全て 階層モデル の特別な場合とみなすことができる（Concept with an attitude）．そこで本稿では全て「階層モデル」と呼んでしまうこととする．
階層モデルには，これがひとたび推定されたのちは，そのモデルからデータをサンプリングすることが出来るという特徴がある．2
1.2.2 ベイズデータ解析
ベイズ統計学の文脈では，こうして得たデータをモデルの正確さの検証に用いることが出来る点が，生成モデルの美点としてみなされている．3
これはベイズ統計学では，階層モデルは物理的過程や社会的過程や因果など，何らかの現実を抽象化したものとみなされるためである．
1.2.3 生成モデリング
一方で生成モデルの文脈では，純粋に「データ分布からの複製」を目標とするため，階層モデルはモデリングの道具ではなく，ひとえに正確なデータ分布を学習するための装置とみなされる．
このように，統計と機械学習とでは階層モデルに対する態度と姿勢が違うのみで，生成モデルとベイズモデリングは数理的には同じ営為であると言える．
このことは表現学習の初期から意識されていたことであり (Kersten et al., 2004), (Yuille and Kersten, 2006)，実際データの背後にある因果構造を正しく特定できている形の階層モデルを推定した際は，その階層的な構造がデータの背後にある因果的な変動要因をうまく分解して陽の下に晒してくれるはずである (Chen et al., 2017)．
| ベイズ統計 | 生成モデル | |
|---|---|---|
| 目標 | 正しいモデルを得る | 高精度の生成をする |
| 生成 | おまけ | 主目的 |
| 価値観 | 不偏性は嬉しい | 精度が重要 |
| 推定法 | MCMC などの Monte Carlo 法 | 変分推論などの最適化 |
1.3 「シミュレーション」としてのサンプリング
1.3.1 「観測」：シミュレーション前夜
現代の科学技術のミトコンドリア・イブは Newton 力学だとする言説に，異論は少ないだろう．
Newton 力学から始まる全ての物理学における理論は，観測データを説明するために作られた．
統計モデルのように尤度を最適化するわけではないが，最もデータをよく説明する模型のみが残ってきたのは物理学も同じである．
Newton 力学の大きなモチベーションに Kepler の三法則の説明があり，この法則は Tycho Brahe の観測から見出されたものである．
ティコ・ブラーエは彼のためにオラネンブルグに建てられたよく整備された「天文台」の中で，同じ一様な製図の上に惑星の位置を書き記すだけでなく，前もって印刷した同じ星図の上に惑星の位置を書き記すだけでなく，前もって印刷した同じ星図をヨーロッパ中の天文学者に送ってそこへ書き記すように求めて，彼らからの観測結果をも集めた． 彼（ティコ・ブラーエのこと）の精神が突然に変化を遂げたのでは無い．彼の目が突然に古い偏見から自由になるのでは無い．以前の誰よりも夏の空を注意深く観測している訳でも無い．彼は，夏の空＋自分の観測＋同僚の観測＋コペルニクスの書物＋プトレマイオスの『アルマゲスト』の多くの版とを一望のもとに見て考えた最初の人物である．長いネットワークの始点と終点に座り，不変で結合可能な可動物を私が呼ぶものを生み出した最初の人物である．(ブルーノ・ラトゥール, 1999)
1.3.2 「実験」：最初のシミュレーション
まもなくして実験が物理学を駆動する方法論となり，長い間物理学においては，実験と理論の２者が相補的な関係にあった．
If it disagrees with experiment, it’s wrong. In that simple statement, is the key to science. (Feynman, 1964)
だが，多くの物理理論は，特定の「この数値を測定すれば良い」というようなところまで提供し，実験はこれを確認する役割を果たすことが多かった．
このようなスキームでは，実験から集中される観察データ自体が複雑な構造を持つということは稀だったと言えるだろう．
1.3.3 「数値実験」：ラボからコンピュータへ
しかし，統計力学の扱う対象などは，例えば Ising 模型など，環境を整えて実験的に再現するということは難しい．その結果，計算機内でのシミュレーションが実験の代わりを果たすようになっている．３次元の Ising 模型の臨界指数の conformal bootstrap による計算 (El-Showk et al., 2012) などはその良い例である．
The computer becomes the virtual laboratory in which a system is studied - a numerical experiment. (Rapaport, 2004, p. 3)
また，天体観測の時代とは違い，データ自体が複雑な構造を持つ一つの宇宙のような様相を呈しているのが計算機時代である．例えば，高次元における測度の集中の現象 (Carlen et al., 2017) が発見されたように，高次元データにおける多様体仮説も広く観察されている (本武陽一, 2017)．
現代では，そのようなデータを料理すること自体が一つの重要な実験技法と言えるかもしれない．
1.3.4 社会「科学」
「数値実験」「シミュレーション」という新たな「実験」技術が，真の意味で社会科学を「科学」たらしめるかもしれない．
Social science is an example of a science which is not a science.
Feynman on the social sciences
結局，このような「社会科学は科学か？」という論争も，自然科学の理論の実験による検証よりも，社会科学の理論の実験による検証の方が，はるかに実験技術の発達を必要とした，というだけに過ぎないかもしれない．
1.3.5 意味論的シミュレーション
大規模言語モデル（LLM）は，物理学的なシミュレーションと相補的な世界モデルを提供しつつある．産業界では，初めて言語を生成できるモデルとして，会話やディスカッションのシミュレーションツールとしても使われている．
加えて，計算科学の意味での数値実験によるシミュレーションだけでなく，生成モデルを汎用物理シミュレーターとして用いる考え方が，Sora (Brooks et al., 2024) の出現以降広まった．
実際，動画の生成・自動運転のシミュレーション・自律的エージェントのシミュレーションなどは，物理法則のシミュレーションとタスクとして一致するところが多い (Zhu et al., 2024)．
1.4 結論：「サンプリングとは輸送である」
2 サンプリングと最適化の双対性
「生成」「シミュレーション」などの「隠れたサンプリング」が多いのと同様，隠れた最適化も多い．ほとんどの物理法則は変分法的解釈を持つ．
2.1 サンプリングによる最適化
統計力学的な系は自由エネルギー最小化原理に従って基底状態に緩和する．
このことにより，最適化にサンプリングが利用できる．模擬アニーリング (Kirkpartick et al., 1983) などはその例と言えよう．
一般に，サンプリングが勾配フリーの最適化ソルバーとして利用可能であることが理解されてきている (Andrieu et al., 2024)．
2.2 最適化によるサンプリング
生成モデルは，その生成の精度が重視されるために，多くの場合は最適化によってベイズ推論問題が解かれる．
3 あとがき
References
Andrieu, C., Chopin, N., Fincato, E., and Gerber, M. (2024). Gradient-free optimization via integration.
Brooks, T., Peebles, B., Holmes, C., DePue, W., Guo, Y., Jing, L., … Ramesh, A. (2024). Video generation models as world simulators. OpenAI. Retrieved from https://openai.com/research/video-generation-models-as-world-simulators
Carlen, E., Madiman, M., and Werner, E. M. (Eds.). (2017). Convexity and concentration,Vol. 161. Springer New York.
Chen, X., Kingma, D. P., Salimans, T., Duan, Y., Dhariwal, P., Schulman, J., … Abbeel, P. (2017). Variational Lossy Autoencoder. In International conference on learning representations.
El-Showk, S., Paulos, M. F., Poland, D., Rychkov, S., Simmons-Duffin, D., and Vichi, A. (2012). Solving the 3D ising model with the conformal bootstrap. Phys. Rev. D, 86, 025022.
Feynman, R. P. (1964). Seeking new laws.
Kersten, D., Mamassian, P., and Yuille, A. (2004). Object perception as bayesian inference. Annual Review of Psychology, 55(Volume 55, 2004), 271–304. Journal Article.
Kirkpartick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680.
Metropolis, N. (1987). The beginning of the monte carlo method. Los Alamos Science Special Issue, 15, 125–130.
Metropolis, Nicholas, and Ulam, S. M. (1949). The monte carlo method. Journal of the American Statistical Association, 44(247), 335–341.
Rapaport, D. C. (2004). The art of molecular dynamics simulation. Cambridge University Press.
Yuille, A., and Kersten, D. (2006). Vision as Bayesian Inference: Analysis by Synthesis? Trends in Cognitive Sciences, 10(7), 301–308.
Zhu, Z., Wang, X., Zhao, W., Min, C., Deng, N., Dou, M., … Huang, G. (2024). Is sora a world simulator? A comprehensive survey on general world models and beyond.
ブルーノ・ラトゥール. (1999). 科学が作られているとき――人類学的考察. 産業図書.
本武陽一. (2017). 高次元データセットに潜む幾何構造と深層学習 : その解析と大自由度力学系への応用 (PhD thesis). 東京大学. Retrieved from https://repository.dl.itc.u-tokyo.ac.jp/records/48134
Footnotes
当時の歴史は (N. Metropolis, 1987) に詳しい．↩︎
圏論的には，射の列を終対象から辿ることにあたる：\(\{*\}\to Z\to X\)．↩︎
特に Richard McElreath の統計観に強く現れている．↩︎