ニューラル常微分方程式
シミュレーションなしの拡散モデルとしての連続正規化流
2024-02-14
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
関連ページ
1 デノイジング拡散模型 (DDPM)
1.1 はじめに
拡散モデルによる画像生成は，初め (Sohl-Dickstein et al., 2015) で提案され，(Ho et al., 2020) で DDPM (Denoising Diffusion Probabilistic Model) として拡張された．
DDPM では訓練データを，完全な Gauss 分布になるような変換を拡散過程によって行う．これを複数段階に分けて実行し，エンコーダー \[ Q(x_0,-)=\int\cdots\int Q^1(x_0,dx_1)\cdots Q^T(x_{T-1},-)=\mathrm{N}_d(0,I_d) \] を得る．
続いて，この逆過程 \(p_\theta(x_t,x_{t-1})\) を VAE 様の方法で変分推論により学習しようというのである．
この方法は，Langevin サンプラーをデータ分布に誘導するスコア場を，種々のノイズレベル \(\sigma_t>0\) で スコアマッチング により学習し，アニーリングをした Langevin サンプラーによりサンプリングをしていることに等価になる．
この SGM (Score-based Generative Model) としての見方（第 2 節）からは，サンプリングに特化した EBM ともみなせる．
この２つの見方はノイズスケジュールの違いを除いて等価な目的関数を定める (Huang et al., 2021)．また，違う SDE が定める異なる拡散課程を用いて，ノイズ分布をデータ分布に輸送しているともみれる (Y. Song, Sohl-Dickstein, et al., 2021)．現状２つの定式化は完全に等価とみなされ，単に 拡散模型 と言った場合 DDPM と SGM の双方を指す．
拡散模型は現在，連続時間ベースのフローベースモデルとして，連続時間正規化流 (CNF) と同一の枠組みで捉えられる (Albergo et al., 2023)．
1.2 エンコーダーの設定
前述の通り，DDPM はエンコーダー \(q\) とデコーダー \(p_\theta\) がそれぞれ複数層からなるような，階層的 VAE ともみなせる．
ただし潜在空間上の事前分布は \(\mathrm{N}_d(0,I_d)\) で固定し，エンコーダー \(q\) は \[ Q(x_0,dx_T)=q(x_0,x_T)\,dx_T=\mathrm{N}_d(0,I_d) \] を満たすように，ノイズスケジュール \(\{\beta_t\}\) の自由度のみをハイパーパラメータとして残して \[ Q^t(x_{t-1},dx_t):=\mathrm{N}_d\left(\sqrt{1-\beta_t}x_{t-1},\beta_tI_d\right),\qquad\beta_t\in(0,1), \] で固定し，学習すべきパラメータは入れない．
このとき \[ Q^{1:t}(x_0,dx_t)=\mathrm{N}_d\left(\sqrt{\alpha_t}x_0,(1-\alpha_t)I_d\right),\qquad\alpha_t:=\prod_{s=1}^t(1-\beta_s), \] であり，後述の通り，これは OU 過程をシミュレーションしていることにあたる（第 3.2 節）．
1.3 デコーダーの設定
核 \(Q^t(x_{t-1},dx_t)\) の逆 \[ q(x_{t-1}|x_t)\,dx_{t-1}dx_t=Q^t(x_{t-1},dx_t)\,dx_{t-1} \] を考えたい．この際，\(x_0\) で条件づけると，次のような表示を得る：
このことに基づいて， \[ P^t_\theta(x_t,dx_{t-1})=\mathrm{N}_d\biggr(\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)\biggl),\qquad\Sigma_\theta(x_t,t):=\sigma_t^2I_d, \tag{1}\] とモデリングする．
総じて，データ分布を \[ p_\theta(x_0)\,dx_0:=\int_{\mathbb{R}^{dT}}p(x_T)P^T_\theta(x_T,dx_{T-1})\cdots P^1_\theta(x_1,dx_0)dx_T \tag{2}\] としてモデリングすることになる．ただし，\(p(x_T)\,dx_T=\mathrm{N}_d(0,I_d)\)．
1.4 DDPM の実装
DDPM (Ho et al., 2020) では，平均のモデリングにのみパラメータを入れて，分散は \[ \Sigma_\theta(x_t,t):=\sigma_t^2I_d,\qquad\sigma^2_t\in\{\beta_t,\widetilde{\beta}_t\} \] としてしまう．
\(\beta_t\) の選択は Taylor 展開を通じた一次近似として正当化されるが，これにもニューラルネットワークを導入してより高次な近似をし，精度を上げる方法が (Nichol and Dhariwal, 2021) で議論されている（第 4.1.2 節）．
加えて，\(x_t,x_0\) で条件付けた \(x_{t-1}\) の平均 \(\widetilde{\mu}_t(x_t,x_0)\) は， \[ x_t=\sqrt{\alpha_t}x_0+\sqrt{1-\alpha_t}\epsilon_t\quad\Leftrightarrow\quad x_0=\frac{1}{\sqrt{\alpha_t}}x_t-\frac{\sqrt{1-\alpha_t}}{\sqrt{\alpha_t}}\epsilon_t,\qquad\epsilon_t\sim\mathrm{N}_d(0,I_d) \] を通じてパラメータ変換を施スト \[\begin{align*} \widetilde{\mu}_t(x_t,\epsilon_t)&=\frac{1}{\sqrt{1-\beta_t}}\left(\frac{1-\alpha_{t-1}}{1-\alpha_t}(1-\beta_t)x_t+\frac{\beta_t}{1-\alpha_t}x_t-\frac{\beta_t}{\sqrt{1-\alpha_t}}\epsilon_t\right)\\ &=\frac{1}{\sqrt{1-\beta_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\alpha_t}}\epsilon_t\right) \end{align*}\] を得る．
従って，\(x_t\) から \(x_{t-1}\) を予測する代わりに，\(x_t\) から「どれくらいデノイジングするか？」を代わりに予測することもできる．すなわち， \[ \widetilde{\mu}_\theta(x_t,t)=\frac{1}{\sqrt{1-\beta_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\alpha_t}}\widetilde{\epsilon}_\theta(x_t,t)\right) \] というパラメータ変換により，\(\widetilde{\mu}_t(x_t,t)\) の代わりに \(\widetilde{\epsilon}_\theta(x_t,t)\) を予測する．
また \(x_t\) は常に \(d\) 次元で一定であるため，アーキテクチャは \(U\)-net や ConvNet などが用いられる．
1.5 訓練
このモデルの対数尤度 (2) は \(\mathbb{R}^{dT}\) 上の積分を含む．そこで VAE 同様，最初の選択が変分推論となる．
次のように \(\mathcal{L}(\theta,q)\) によって下から評価できる：
\[\begin{align*} \log p_\theta(x_0)&=\log\int_{\mathbb{R}^{dT}}p_\theta(x_{0:T})\,dx_{1:T}\\ &=\log\left(\int_{\mathbb{R}^{dT}}\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}q(x_{1:T}|x_0)\,dx_{1:T}\right)\\ &\ge\int_{\mathbb{R}^{dT}}\log\left(p(x_T)\prod_{t=1}^T\frac{p_\theta(x_{t-1}|x_t)}{q(x_t|x_{t-1})}\right)q(x_{1:T}|x_0)\,dx_{1:T}\\ &=:\mathcal{L}(\theta,q). \end{align*}\]
ただし，\(\mathcal{L}(\theta,q)\) は次のように変形できる：
\[\begin{align*} \mathcal{L}(\theta,q)&=-\operatorname{KL}\biggr(q(x_T|x_0),p(x_T)\biggl)\\ &\qquad-\sum_{t=2}^T\int_{\mathbb{R}^d}\operatorname{KL}\biggr(q(x_{t-1}|x_t,x_0),p_\theta(x_{t-1}|x_t)\biggl)q(x_t|x_0)\,dx_t\\ &\qquad+\int_{\mathbb{R}^d}\log p_\theta(x_0|x_1)q(x_1|x_0)\,dx_1\\ &=:\mathcal{L}_1(q)+\mathcal{L}_2(\theta,q)+\mathcal{L}_3(\theta,q). \end{align*}\]
この式は VAE の変分下界 から，KL 乖離度の項が \(T-1\) 個増えた形になっている．
この変分下界 \(\mathcal{L}(\theta,q)\) の無限次元変数 \(q\) の方は，\(x\) からスタートするエンコーダー過程 1.2 の確率核に固定してしまう．
すると，第二項 \(\mathcal{L}_2(\theta)\) に登場する密度は全て正規密度であるため，解析的に計算できる： \[ \operatorname{KL}\biggr(q(x_{t-1}|x_t,x_0),p_\theta(x_{t-1}|x_t)\biggl)=\frac{\lvert\widetilde{\mu}_t(x_t,x_0)-\mu_\theta(x_t,t)\rvert^2}{2\beta_t}. \] 第三項 \(\mathcal{L}_3(\theta)\) は \(q(x_1|x_0)\,dx_1=\mathrm{N}_d(\sqrt{1-\beta_1}x_0,\beta_1I_d)\) からのサンプルにより Monte Carlo 近似できる．
1.6 代理目標
DDPM (Ho et al., 2020) では，\(\widetilde{\mu}_\theta(x_t,t)\) の代わりに，\(\widetilde{\epsilon}_\theta(x_t,t)\) を予測するのであった（第 1.4 節）．
この際，第三項は次の変更を受ける： \[ \operatorname{KL}\biggr(q(x_{t-1}|x_t,x_0),p_\theta(x_{t-1}|x_t)\biggl)=\frac{\beta_t}{2(1-\alpha_t)(1-\beta_t)}\biggl|\widetilde{\epsilon}_\theta\biggr(\sqrt{\alpha_t}x_0+\sqrt{1-\alpha_t}\epsilon_t,t\biggl)-\epsilon_t\biggr|^2+\mathrm{const.} \] 第二項も全く同じ表記になり，\(t=1\) の場合に当たるから，総じて \[ \mathcal{L}(\theta)=-\sum_{t=1}^T\frac{\beta_t}{2(1-\alpha_t)(1-\beta_t)}\biggl|\widetilde{\epsilon}_\theta\biggr(\sqrt{\alpha_t}x_0+\sqrt{1-\alpha_t}\epsilon_t,t\biggl)-\epsilon_t\biggr|^2+\mathrm{const.} \]
しかし，DDPM (Ho et al., 2020) では，正確な変分推論を実行するのではなく，この係数を全て \(1\) にした \[ \mathcal{L}'=\lvert\epsilon_\tau-\widetilde{\epsilon}_\theta(X_\tau,\tau)\rvert^2,\qquad X_\tau=\sqrt{\alpha_\tau}X_0+\sqrt{1-\alpha_\tau}\epsilon_\tau,\tau\sim\mathrm{U}([T]),X_0\sim p(x_0)\,dx_0,\epsilon_\tau\sim\mathrm{N}_d(0,I_d), \] を代理目標として用いた．ただし，\(p(x_0)\,dx_0\) はデータ分布である．
これは純粋に，時刻 \(t\) までに実際に印加されるノイズ \(\epsilon_t\) とモデルが予測するノイズ \(\widetilde{\epsilon}_\theta\) の二乗差を最小化することに等しい．
この目的関数の変更は，\(t\) が小さい場合の誤差を小さく評価し，\(t\) が大きい場合の誤差を大きく評価するため，大きい \(t\) でのデノイジングというより難しいタスクを強調して学習する効果を持つという (Ho et al., 2020)．
(Choi et al., 2022) この代理目標の議論をさらに進めている．またこのような代理目標は，データ拡張の下では真の ELBO と一致する (D. Kingma and Gao, 2023) ため，全く無根拠な変更というわけではない．
1.7 最尤推定
VDM (Variational Diffusion Model) (D. P. Kingma et al., 2021) では正確に \(\mathcal{L}(\theta)\) を最小化することで最尤推定を実行する．
この方法では DDPM では固定されていたノイズスケジュール \(\widetilde{\beta}_t\) の真の変分推論が実行できる．
\[ Q^{1:t}(x_0,dx_t)=\mathrm{N}_d\biggr(\sqrt{\alpha_t}x_0,(1-\alpha_t)I_d\biggl) \] の変数 \(\alpha_t\) をパラメータ変換した SNR (Signal-to-Noise Ratio) \[ R(t)=\frac{\alpha_t}{1-\alpha_t}=:e^{-\gamma_\phi(t)} \] に注目し，\(\gamma_\phi\) をニューラルネットワークでモデリングする．
この \(R(t)\) を用いれば，正確な目的関数 \(\mathcal{L}(\theta)\) はより簡単な表示を持つことを発見した (D. P. Kingma et al., 2021) は，さらにこれを訓練する際に QMC によるより分散の小さい Monte Carlo 推定量を用いることで，DDPM と同じくらい効率的に最尤推定が実行できることを示した．
(D. P. Kingma et al., 2021), (Huang et al., 2021) は無限層の VAE という DDPM の観点からの貢献であるが，SDE の観点からの最尤推定法を (Y. Song, Durkan, et al., 2021), (Vahdat et al., 2021) が提案している（第 2.6 節）．
2 スコアベースの生成模型 (SGM)
2.1 はじめに
スコアマッチングはもともと，エネルギーベースモデル (EBM) の学習手法として (Hyvärinen, 2005) により提案された．
そもそも EBM も優秀な生成モデルとして知られている (Du and Mordatch, 2019), (Gao et al., 2020) が，スコアマッチングによるスコアの学習はもっと直接的に生成モデルを定める：
これが SGM (Score-based Generative Model) (Y. Song and Ermon, 2019) のアイデアであった．1
このアイデアは既存の DSM (Denoising Score Matching) の改良とも見れる．
DSM はデータに印加するノイズ \(\sigma>0\) が強いほど推定が安定するが，推定対象であるノイズが印加されたスコアは元のデータ分布から乖離してしまうというトレードオフがあった．これをアニーリングによって解決する方法とも見れる．
2.2 SGM の課題
しかしこのスキームの課題は，\(\nabla_x\log p(x)\) の値は \(p\) を一意的に定めないということである．
例えば， \[ p=\pi p_0+(1-\pi)p_1,\qquad\pi\in(0,1) \] という関係があり，\(p_0,p_1\) の台が互いに素であったとき，\(\nabla_x\log p\) からは \(\pi\in(0,1)\) を定めるための情報が完全に消えてしまう．
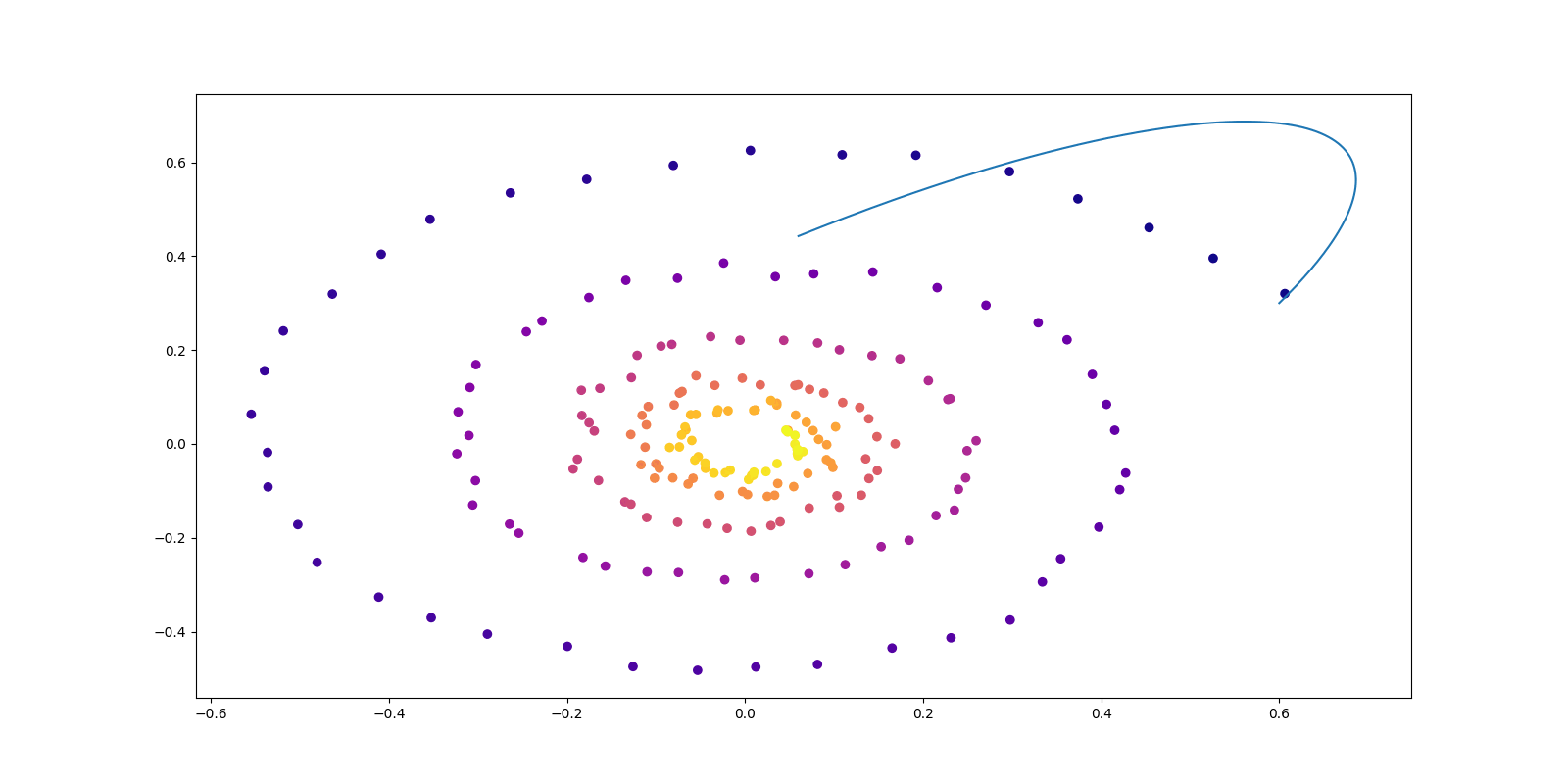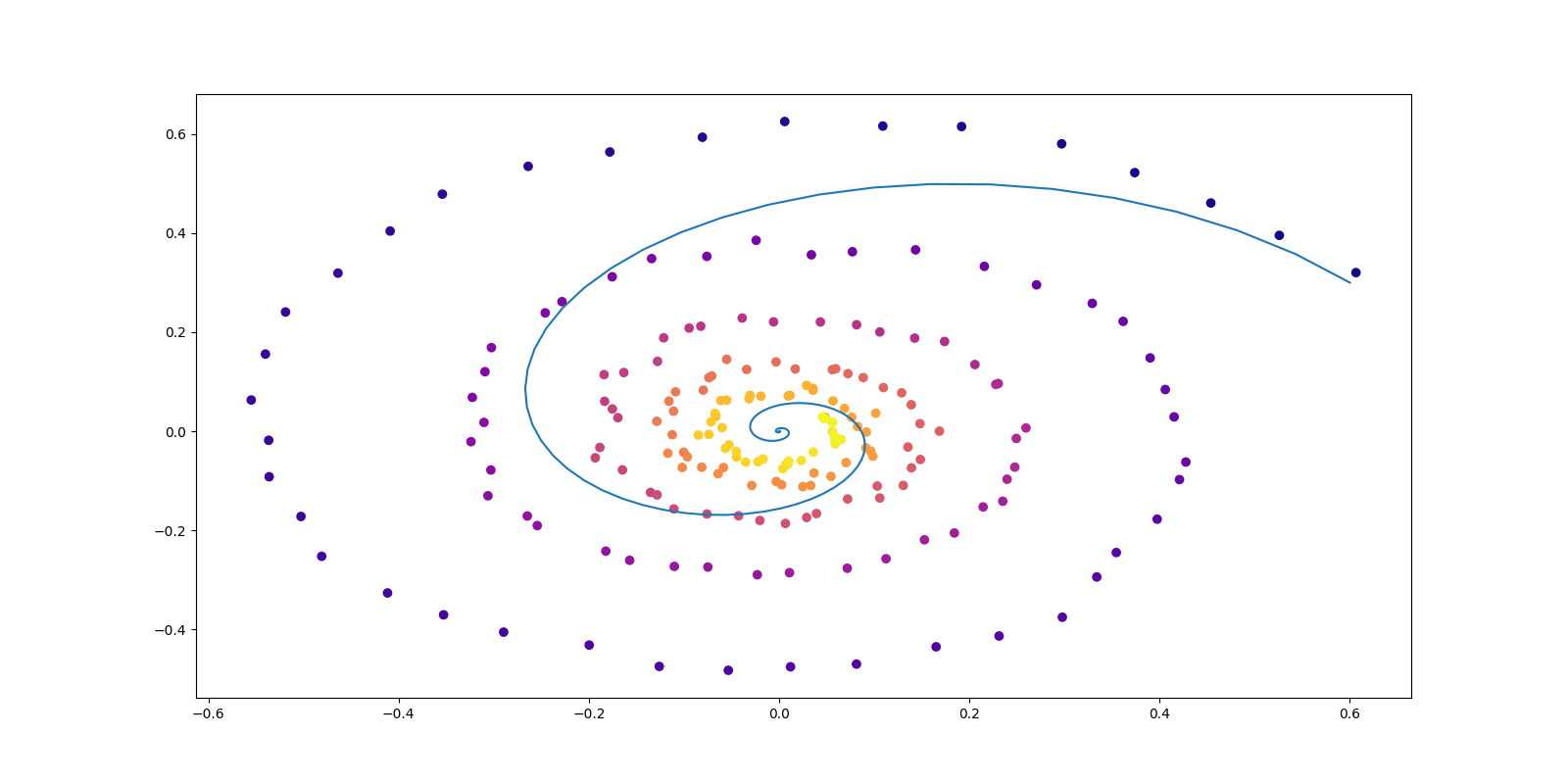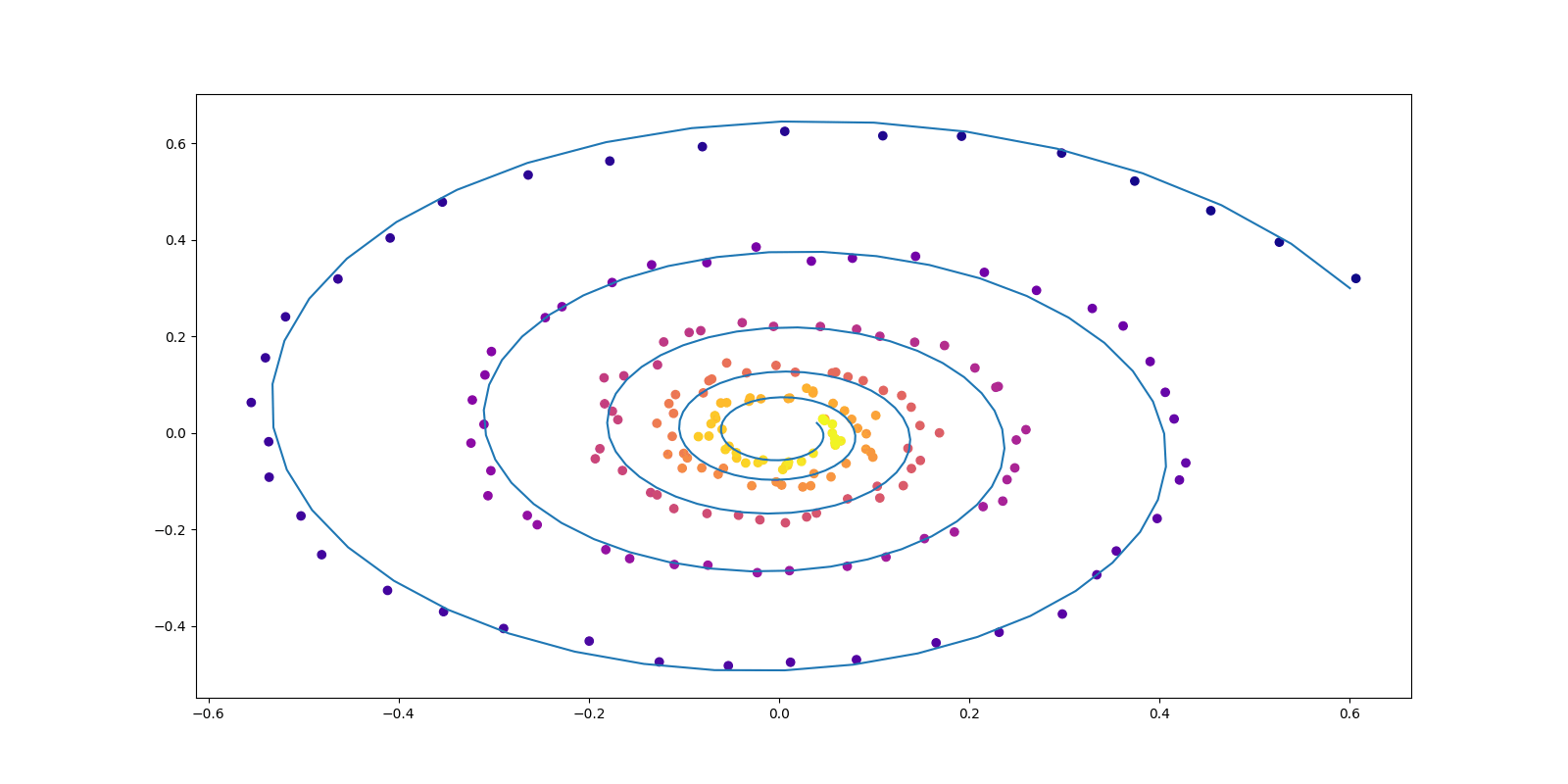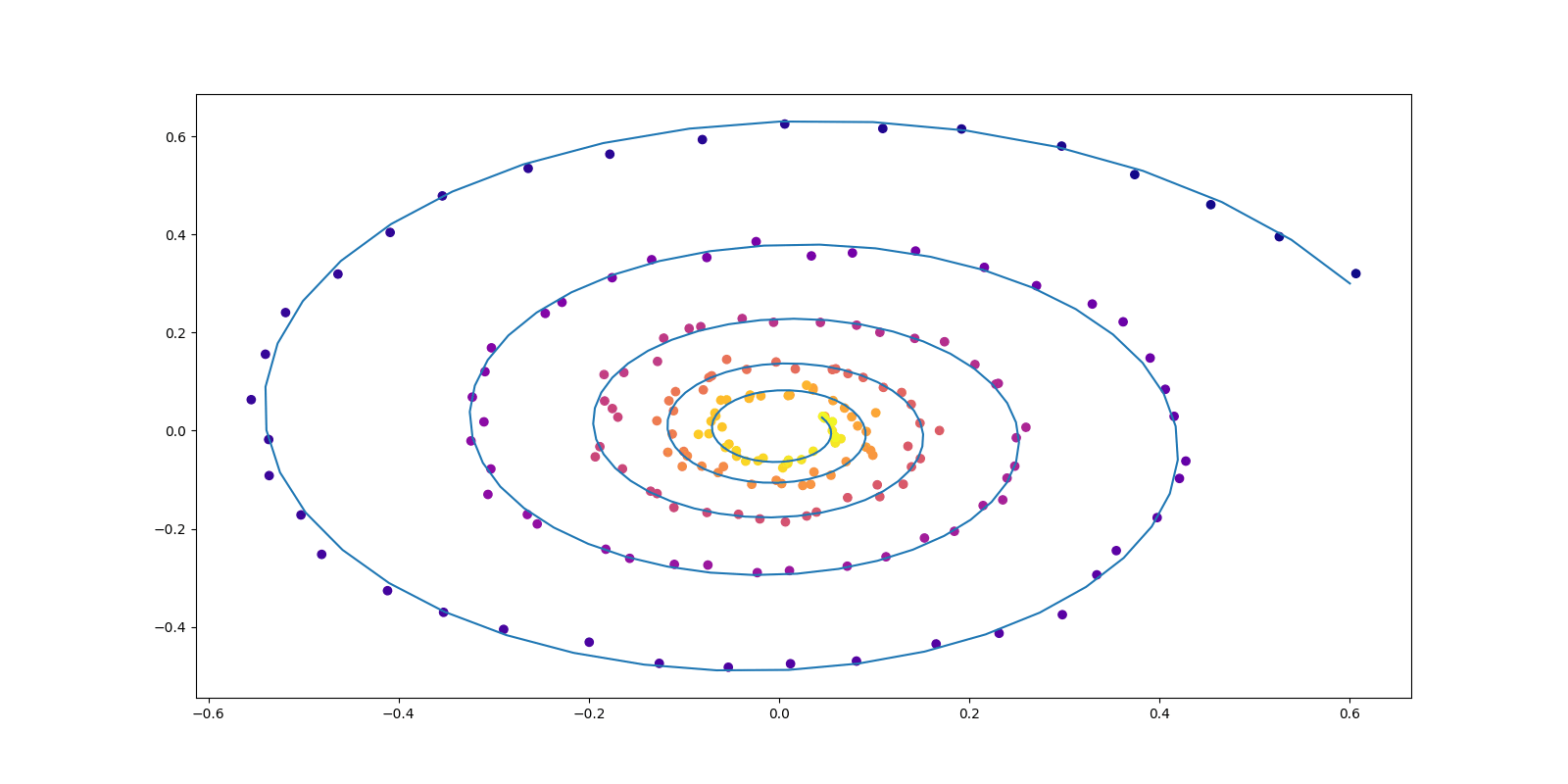
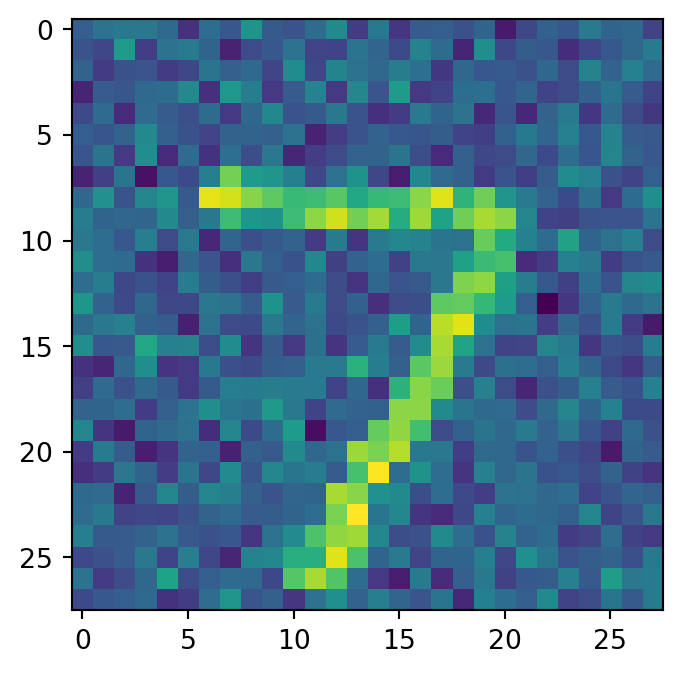
すなわち，データが下図のように部分多様体上にのみ台を持つ場合は，モデルが識別可能でない．
これにより間違ったスコアが学習され，多峰性を持ってしまった場合，OU 過程によるサンプリングが失敗する (Y. Song and Ermon, 2019)．
従って，各ノイズレベル \(\sigma\) に対応したスコア場を学習し，Langevin サンプラーをノイズが大きく分布が単純な領域からスタートさせ，徐々にデータ分布に近づけて収束を促す（アニーリング）．
すると SGM は，最初の発想は全く違えど，最終的に得られるモデルは，DDPM と等価になる．
2.3 デノイジングによる解決
SGM (Y. Song and Ermon, 2019), (Y. Song and Ermon, 2020) ではデータにさまざまな強度 \(\sigma\) の Gauss ノイズを印加したもののスコア場を，スコアマッチングで学習することを考える．
ノイズレベル \(\sigma\) も入力に含めることで，単一のニューラルネットワーク \(s_\theta(x,\sigma)\) で学習をする．このアーキテクチャを NCSN (Noise Conditional Score Network) (Y. Song and Ermon, 2019) または単に スコアネットワーク (Y. Song and Ermon, 2020) という．
ノイズを印加することは，Gauss 核との畳み込みにより分布を軟化していくことに相当し，アニーリングと同じ効果を持つ．
その結果，\(\sigma\) が十分大きい際は多峰性が消失してスコアマッチングが正確になる．加えて MCMC によるサンプリングも容易になる．
はじめ，OU 過程を十分に大きい \(\sigma>0\) に対応するスコアで駆動させ，徐々に \(\sigma\to0\) としていくことで，データ分布からサンプリングすることを目指す．2
2.4 目的関数
スコアのスケール \(\sigma\) の Gauss ノイズにより軟化したデータのスコア場を \(s_\theta(x,\sigma)\) と表し，デノイジングスコアマッチング (DNS) の目的関数の列を考える：3 \[ \mathcal{L}(\theta;\sigma)=\frac{1}{2}\operatorname{E}\left[\left\|s_\theta(\widetilde{X},\sigma)+\frac{\widetilde{X}-X}{\sigma^2}\right\|^2_2\right]. \]
この DNS 目的関数の，ある等比数列 \(\sigma_1>\cdots>\sigma_T>0\) に関する線型和 \[ \mathcal{L}(\theta;\sigma_{1:T})=\sum_{t=1}^T\lambda_t\mathcal{L}(\theta;\sigma_t),\qquad\lambda_t>0, \tag{3}\] を最終的な目的関数とする．
数列 \((\sigma_i)\) の設定の仕方，\(\sigma_1\) をどこまで大きくすれば良いか，などは (Y. Song and Ermon, 2020) の理論解析を参照．ステップ数 \(T\) は大きければ大きいほどよい．
2.5 DDPM との対応
この SGM の目的関数 (3) は，ノイズスケジュール \(\lambda_t\) が異なるのみで DDPM 1 と同じ目的関数となっている (Ho et al., 2020), (Huang et al., 2021)．
実際， \[ \mathcal{L}(\theta;\sigma_t^2)=\operatorname{E}\left[\frac{\lambda_\tau}{\sigma_\tau^2}\lvert\epsilon_\tau-\widetilde{\epsilon}_\theta(X_\tau,\tau)\rvert^2\right] \] と表せるから，ハイパーパラメータ \(\lambda_t\) を \(\lambda_t=\sigma_t^2\) と取ることで，DDPM の代理目的関数 1.6 に一致する．
2.6 最尤推定
近似が入っている DDPM の訓練目標と対応していることから判るように，スコアマッチングは正確な最尤推定を実行していない．
かといって，正確な変分推論 1.7 を実行するのは高くつく．
(Y. Song, Durkan, et al., 2021) はスコアマッチングと同じくらい効率的な最尤推定法が，目的関数 (3) の重みづけ \((\lambda_t)\) を特定の値 likelihood weighting にとることで得られることを示している．4
.png)
3 連続時間極限
3.1 はじめに
DDPM 1 と SGM 2 は，いずれも OU 過程とその時間反転の離散化として統一的に理解できる．
この連続時間極限に関する知見が，モデルのデザインに関して示唆を与えてくれる (Tzen and Raginsky, 2019), (Y. Song, Sohl-Dickstein, et al., 2021)．
タイムステップ \(t\) の取り方は適応的にできるし，5 SDE (4) と等価な輸送を定める ODE を考え，サンプリングを加速することも考えられる．6
3.2 前向き拡散過程
データ分布を正規分布に還元する際に DDPM 1 で用いた拡散過程は，パラメータ \(\beta(t)\) を持った \(0\) に回帰的な OU 過程である (Y. Song, Sohl-Dickstein, et al., 2021, p. 5)： \[ dX_t=-\frac{\beta(t)}{2}X_tdt+\sqrt{\beta(t)}dB_t,\qquad\beta\left(\frac{t}{T}\right)=T\beta_t. \tag{4}\]
これを (Y. Song, Sohl-Dickstein, et al., 2021) では 分散保存過程 (variance-preserving process) と呼んでいる．
一方で，SGM 2 では \[ dX_t=\sqrt{\frac{d }{d t}\sigma(t)^2}dB_t \] で定まる拡散過程を用いる．これを (Y. Song, Sohl-Dickstein, et al., 2021) では 分散爆発過程 (variance-exploding process) と呼んでいる．
3.3 後ろ向き拡散
(Anderson, 1982) によると，一般に \[ dX_t=f_t(X_t)\,dt+\sigma_t\,dB_t \] という SDE の時間反転 は， \[ dY_t=\biggr(f_t(Y_t)-\sigma_t^2\nabla_x\log q_t(Y_t)\biggl)\,dt+\sigma_t\,dB_{-t} \] が定める．ここにスコア場 \(\nabla_x\log q_t\) が出てくるのである．
特に，OU 過程 (4) の時間反転は \[ dY_t=\biggr(-\frac{\beta_t}{2}Y_t-\beta_t\nabla_{x}\log q_t(Y_t)\biggl)\,dt+\sqrt{\beta_t}\,dB_{-t} \] と表せる．
このスコア関数 \(\nabla_x\log q_t(X_t)\) を DSM によって推定した \[ dY_t=-\frac{\beta_t}{2}\biggr(Y_t+2s_\theta(Y_t,t)\biggl)\,dt+\sqrt{\beta_t}\,dB_{-t} \] でデータ分布からサンプリングすることができるのである．なお，拡散過程のサンプリングは難しい問題であり，最も直接的には Euler-Maruyama 離散化を通じれば良い．
3.4 等価な輸送を定める確定的ダイナミクス
代わりに ODE \[ \frac{d x_t}{d t}=f(x,t)-\frac{g(t)^2}{2}\nabla_x\log p_t(x) \] で定まる確定的ダイナミクス \(\{x_t\}\) を用いても，同様にデータ分布は \(\mathrm{N}_d(0,I_d)\) に還元される．
これを (Y. Song, Sohl-Dickstein, et al., 2021 Sec D.3) は probability flow ODE と呼ぶ．
3.5 後ろ向き ODE
この ODE を推定した \[ \frac{d y_t}{d t}=f(y,t)-\frac{g(t)^2}{2}s_\theta(y_t,t) \] を Euler 法，またはより高次な Heun 法などによって逆から解くことができる (Karras et al., 2022)．
これは連続時間正規化流，特に Neural ODE と等価なモデリングをすることになる．
実は SDE は \[ dY_t=\biggr(f(y,t)-\frac{g(t)^2}{2}s_\theta(y_t,t)\biggl)-\frac{\beta_t}{2}s_\theta(y_t,t)dt+\sqrt{\beta_t}\,dB_t \] と，上記の確率的フロー ODE に OU 過程の項を加えた形になっており，ODE によるアプローチはこの追加の OU 過程項を消去することに等しい．
4 応用
4.1 サンプリング加速法
ODE を用いることで拡散模型のサンプリング速度が向上する．(Nichol and Dhariwal, 2021) も参照．
4.1.1 Denoising Diffusion Implicit Model (DDIM) (J. Song et al., 2021)
DDIM (J. Song et al., 2021) は，スタート地点 \(x_0\) に条件付けられた確率核 \[ q_\sigma(x_{t-1}|x_t,x_0)\,dx_{t-1}=\mathrm{N}\biggr(\sqrt{\alpha_{t-1}}x_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\frac{x_t-\sqrt{\alpha_t}x_0}{\sqrt{1-\alpha_t}},\sigma_t^2I_d\biggl) \tag{5}\] を考える．7 これを \(x_0\) に関して積分すると元の確率核 \(q_\sigma(x_{t-1}|x_t)\) を得る．
\(\sigma_t\) は任意としており， \[ \sigma_t=\sqrt{\frac{1-\alpha_{t-1}}{1-\alpha_t}}\sqrt{1-\frac{\alpha_t}{\alpha_{t-1}}} \] と取った場合，\(q_\sigma(x_{t-1}|x_t,x_0)\) は \(x_0\) にもはや依らず，DDPM の設定を回復する．
\(q_\sigma(x_{t-1}|x_t,x_0)\) の時間反転は次のように与えられる： \[ p_\theta(x_{t-1}|x_t)\,dx_{t-1}=\mathrm{N}\biggr(\sqrt{\alpha_{t-1}}\widehat{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2}\frac{x_t-\sqrt{\alpha_t}\widehat{x}_0}{\sqrt{1-\alpha_t}},\sigma_t^2I_d\biggl). \]
ただし，\(x_0\) は事前にはわからないから，これをニューラルネットワークによりモデリングするとする： \[ \widehat{x}_0=\frac{x_t-\sqrt{1-\alpha_t}\epsilon_\theta(x_t,t)}{\sqrt{\alpha_t}}. \]
すると，この際の目的関数は DDPM と全く変わらない．すなわち，既存の DDPM の訓練は特別な \(\sigma_t\) に関する DDIM (5) の訓練とみなせるのである．
\(\sigma_t\) が自由となると，\(\sigma_t\equiv0\) と取っても良いはずである．この場合，サンプリングの過程は確定的になる．
総じて，すでに訓練された DDPM の \(\epsilon_\theta(x_t,t)\) があれば，この \(\sigma_t\equiv0\) の場合のサンプリング過程を採用すれば，DDPM 1 より 10 倍から 50 倍速いサンプリングが実現できる．
4.1.2 逐次サンプリング問題としての解決
デコーダーに用いるモデル (2) の表現力を上げることで，ステップサイズを大きくしてもサンプリングの性能を悪化させないようにできる．
(Nichol and Dhariwal, 2021) は \(\Sigma_\theta(x_t,t)\) もニューラルネットワークで学習することで，サンプリングのステップサイズを大きくしてもサンプルの質を保つことができると報告している．
(D. P. Kingma et al., 2021) も，ノイズスケジュールも学習しようとしている点で似ている．
(Gao et al., 2021) は，ノイズ分布からデータ分布までのアニーリング列を，EBM の列として捉えてフィッティングをしている．同様のスキームで，(Xiao et al., 2022) は GAN を用いている．
4.1.3 蒸留
(Salimans and Ho, 2022) は Progressive Distillation と呼ばれる拡散過程の蒸留手法を提案している．
学習済みの拡散モデル（(Salimans and Ho, 2022) では DDIM）から，徐々にステップ数を減らした蒸留モデルを作成していく．
4.1.4 潜在拡散模型 (LDM) (Rombach et al., 2022)
まず画像データを VAE などで学習した潜在空間に変換し，その上で拡散模型でモデリングをする．
Latent Score-based Generative Model (LSGM) (Vahdat et al., 2021) では，VAE と拡散模型を同時に訓練することを考えている．
この手法は，潜在表現さえ適切に見つければ，複数のドメインのデータを同時に扱えるという美点がある．
また，(Pandey et al., 2022) では，まず VAE による生成モデルと作成し，その精度が足りない最終的な出力を高画質にするステップにのみ拡散模型を用いるスキームを提案している．
4.1.5 SDE から ODE へ (DEIS)
DEIS (Diffusion Exponential Integrator Sampler) (Zhang and Chen, 2023) では，付随する ODE 3.5 を Euler 法ではなく指数積分法で解くことで，離散化誤差を低減しつつサンプリングを加速する．
4.2 拡散モデルの例
4.2.1 ADM (Dhariwal and Nichol, 2021)
ADM (Ablated Diffusion Model) (Dhariwal and Nichol, 2021) と 分類器による誘導 は ImageNet データの判別において当時の最先端であった BigGAN (Brock et al., 2019) の性能を凌駕した．
そのアーキテクチャには U-Net (Ronneberger et al., 2015) が用いられた．
4.2.2 GLIDE (Nichol et al., 2022)
OpenAI の GLIDE (Guided Language to Image Diffusion for Generation and Editing) (Nichol et al., 2022) は，CLIP (Contrastive Language-Image Pre-training) というトランスフォーマーベースの対照学習による画像テキスト同時表現学習器と組み合わされた，テキスト誘導付き拡散モデルである．
4.2.3 Imagen (Saharia, Chan, Saxena, et al., 2022)
Google も Imagen (Saharia, Chan, Saxena, et al., 2022) という Cascaded Generation (Ho et al., 2022) に基づいた誘導付き拡散モデルを開発している．
T5-XXL (Raffel et al., 2020) に基づく言語モデルを通じて言語と画像を同等の潜在空間にのせ，U-Net アーキテクチャを持った VDM 1.7 でモデリングすることで，高精度な text-to-image を実現している．
Palette (Saharia, Chan, Chang, et al., 2022) は同様の仕組みで image-to-image を実現している．
4.2.4 潜在拡散模型
VAE や GAN と違い，１つのニューラルネットワークしか用いないため，学習が安定しやすい．
一方で，生成時には逆変換を何度も繰り返す必要があるため，計算量が大きい．これを回避するために，生成を VAE 内の潜在空間で行うものを 潜在拡散モデル (latent diffusion model) (Rombach et al., 2022) という．これが Stable Diffusion の元となっている．
4.2.5 トランスフォーマーとの邂逅
並列化が容易であり，スケーラブルな手法であるため，トランスフォーマーと組み合わせて画像と動画の生成に使われる．
潜在拡散モデルで U-Net (Ronneberger et al., 2015) を用いていたところをトランスフォーマーに置換した 拡散トランスフォーマー (DiT: Diffusion Transformer) (Peebles and Xie, 2023) が発表された．
その後，確率的補間 によって DiT を改良した SiT (Scalable Interpolant Transformer) (Ma et al., 2024) が発表された．
4.2.6 Discrete Denoising Diffusion Probabilistic Models (D3PM) (Austin et al., 2021)
Imagen にように言語を連続な潜在空間に埋め込む他に，直接離散空間上にも拡散模型を用いる事ができる．
実はこのように設計された拡散模型は，BERT (Lewis et al., 2020) などのマスク付き言語モデルと等価になる．
MaskGIT (Masked Generative Image Transformer) (Chang et al., 2022) はこの枠組みに，画像をベクトル量子化して載せる．
5 参考文献
Awesome-Diffusion-Models，What’s the score?．
良いサーベイには次がある：(Luo, 2022)，(McAllester, 2023)．古くからあり，すでに出版されているものには，(Yang et al., 2023), (Cao et al., 2024)．
CVPR のチュートリアルが (Kreis et al., 2022), (J. Song et al., 2023)．Web サイトには (Dieleman, 2023)，(Yuan, 2024)，(Duan, 2023)，(Das, 2024)．
また，入門的な内容が (Nakkiran et al., 2024) で扱われている．
拡散モデルのサンプリングを加速する手法に関する論文には (Nichol and Dhariwal, 2021), (Croitoru et al., 2023) など．
References
Albergo, M. S., Boffi, N. M., and Vanden-Eijnden, E. (2023). Stochastic Interpolants: A Unifying Framework for Flows and Diffusions.
Anderson, B. D. O. (1982). Reverse-time diffusion equation models. Stochastic Processes and Their Applications, 12(3), 313–326.
Austin, J., Johnson, D. D., Ho, J., Tarlow, D., and Berg, R. van den. (2021). Structured denoising diffusion models in discrete state-spaces. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems,Vol. 34, pages 17981–17993. Curran Associates, Inc.
Brock, A., Donahue, J., and Simonyan, K. (2019). Large scale GAN training for high fidelity natural image synthesis.
Cao, H., Tan, C., Gao, Z., Xu, Y., Chen, G., Heng, P.-A., and Li, S. Z. (2024). A survey on generative diffusion models. IEEE Transactions on Knowledge and Data Engineering, 36(7), 2814–2830.
Chang, H., Zhang, H., Jiang, L., Liu, C., and Freeman, W. T. (2022). MaskGIT: Masked generative image transformer. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), pages 11315–11325.
Choi, J., Lee, J., Shin, C., Kim, S., Kim, H., and Yoon, S. (2022). Perception prioritized training of diffusion models. In 2022 IEEE/CVF conference on computer vision and pattern recognition (CVPR), pages 11462–11471.
Croitoru, F., Hondru, V., Ionescu, R., and Shah, M. (2023). Diffusion models in vision: A survey. IEEE Transactions on Pattern Analysis &Amp; Machine Intelligence, 45(09), 10850–10869.
Das, A. (2024). Building diffusion model’s theory from ground up. In ICLR blogposts 2024.
Dhariwal, P., and Nichol, A. Q. (2021). Diffusion models beat GANs on image synthesis. In A. Beygelzimer, Y. Dauphin, P. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems.
Dieleman, S. (2023). Perspectives on diffusion.
Du, Y., and Mordatch, I. (2019). Implicit Generation and Modeling with Energy Based Models. In H. Wallach, H. Larochelle, A. Beygelzimer, F. dAlché-Buc, E. Fox, and R. Garnett, editors, Advances in neural information processing systems,Vol. 32. Curran Associates, Inc.
Duan, T. (2023). Diffusion models from scratch.
Gao, R., Nijkamp, E., Kingma, D. P., Xu, Z., Dai, A. M., and Wu, Y. N. (2020). Flow contrastive estimation of energy-based models. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR).
Gao, R., Song, Y., Poole, B., Wu, Y. N., and Kingma, D. P. (2021). Learning energy-based models by diffusion recovery likelihood. In International conference on learning representations.
Ho, J., Jain, A., and Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. In Advances in neural information processing systems,Vol. 33.
Ho, J., Saharia, C., Chan, W., Fleet, D. J., Norouzi, M., and Salimans, T. (2022). Cascaded diffusion models for high fidelity image generation. Journal of Machine Learning Research, 23(47), 1–33.
Huang, C.-W., Lim, J. H., and Courville, A. (2021). A Variational Perspective on Diffusion-Based Generative Models and Score Matching. In A. Beygelzimer, Y. Dauphin, P. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems.
Hyvärinen, A. (2005). Estimation of non-normalized statistical models by score matching. Journal of Machine Learning Research, 6(24), 695–709.
Karras, T., Aittala, M., Aila, T., and Laine, S. (2022). Elucidating the design space of diffusion-based generative models. In A. H. Oh, A. Agarwal, D. Belgrave, and K. Cho, editors, Advances in neural information processing systems.
Kingma, D. P., Salimans, T., Poole, B., and Ho, J. (2021). Variational diffusion models. In Proceedings of the 35th international conference on neural information processing systems. Red Hook, NY, USA: Curran Associates Inc.
Kingma, D., and Gao, R. (2023). Understanding diffusion objectives as the ELBO with simple data augmentation. In A. Oh, T. Naumann, A. Globerson, K. Saenko, M. Hardt, and S. Levine, editors, Advances in neural information processing systems,Vol. 36, pages 65484–65516. Curran Associates, Inc.
Kirkpartick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680.
Kreis, K., Gao, R., and Vahdat, A. (2022). Denoising diffusion-based generative modeling: Foundations and applications.
Lewis, M., Liu, Y., Goyal, N., Ghazvininejad, M., Mohamed, A., Levy, O., … Zettlemoyer, L. (2020). BART: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. In D. Jurafsky, J. Chai, N. Schluter, and J. Tetreault, editors, Proceedings of the 58th annual meeting of the association for computational linguistics, pages 7871–7880. Online: Association for Computational Linguistics.
Liu, Q., Lee, J., and Jordan, M. (2016). A kernelized stein discrepancy for goodness-of-fit tests. In M. F. Balcan and K. Q. Weinberger, editors, Proceedings of the 33rd international conference on machine learning,Vol. 48, pages 276–284. New York, New York, USA: PMLR.
Luo, C. (2022). Understanding diffusion models: A unified perspective.
Ma, N., Goldstein, M., Albergo, M. S., Boffi, N. M., Vanden-Eijnden, E., and Xie, S. (2024). SiT: Exploring flow and diffusion-based generative models with scalable interpolant transformers.
McAllester, D. (2023). On the mathematics of diffusion models.
Nakkiran, P., Bradley, A., Zhou, H., and Advani, M. (2024). Step-by-step diffusion: An elementary tutorial.
Neal, R. M. (2001). Annealed Importance Sampling. Statistics and Computing, 11, 125–139.
Nichol, A. Q., and Dhariwal, P. (2021). Improved Denoising Diffusion Probabilistic Models. In M. Meila and T. Zhang, editors, Proceedings of the 38th international conference on machine learning,Vol. 139, pages 8162–8171. PMLR.
Nichol, A. Q., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., Mcgrew, B., … Chen, M. (2022). GLIDE: Towards photorealistic image generation and editing with text-guided diffusion models. In K. Chaudhuri, S. Jegelka, L. Song, C. Szepesvari, G. Niu, and S. Sabato, editors, Proceedings of the 39th international conference on machine learning,Vol. 162, pages 16784–16804. PMLR.
Pandey, K., Mukherjee, A., Rai, P., and Kumar, A. (2022). DiffuseVAE: Efficient, controllable and high-fidelity generation from low-dimensional latents. Transactions on Machine Learning Research.
Peebles, W., and Xie, S. (2023). Scalable diffusion models with transformers. In Proceedings of the IEEE/CVF international conference on computer vision (ICCV), pages 4195–4205.
Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., … Liu, P. J. (2020). Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res., 21(1).
Rombach, R., Blattmann, A., Lorenz, D., Esser, P., and Ommer, B. (2022). High-resolution image systhesis with latent diffusion models. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (CVPR), pages 10684–10695.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. In N. Navab, J. Hornegger, W. M. Wells, and A. F. Frangi, editors, Medical image computing and computer-assisted intervention – MICCAI 2015, pages 234–241. Cham: Springer International Publishing.
Saharia, C., Chan, W., Chang, H., Lee, C. A., Ho, J., Salimans, T., … Norouzi, M. (2022). Palette: Image-to-Image Diffusion Models.
Saharia, C., Chan, W., Saxena, S., Li, L., Whang, J., Denton, E., … Norouzi, M. (2022). Photorealistic text-to-image diffusion models with deep language understanding. In A. H. Oh, A. Agarwal, D. Belgrave, and K. Cho, editors, Advances in neural information processing systems.
Salimans, T., and Ho, J. (2021). Should EBMs model the energy or the score? In Energy based models workshop - ICLR 2021.
Salimans, T., and Ho, J. (2022). Progressive distillation for fast sampling of diffusion models. In International conference on learning representations.
Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., and Ganguli, S. (2015). Deep Unsupervised Learning using Nonequilibrium Thermodynamics. In F. Bach and D. Blei, editors, Proceedings of the 32nd international conference on machine learning,Vol. 37, pages 2256–2265. Lille, France: PMLR.
Song, J., Meng, C., and Ermon, S. (2021). Denoising diffusion implicit models. In International conference on learning representations.
Song, J., Meng, C., and Vahdat, A. (2023). Denoising diffusion models: A generative learning big bang.
Song, Y., Durkan, C., Murray, I., and Ermon, S. (2021). Maximum Likelihood Training of Score-Based Diffusion Models. In Advances in neural information processing systems,Vol. 34.
Song, Y., and Ermon, S. (2019). Generative Modeling by Estimating Gradients of the Data Distribution. In H. Wallach, H. Larochelle, A. Beygelzimer, F. dAlché-Buc, E. Fox, and R. Garnett, editors, Advances in neural information processing systems,Vol. 32. Curran Associates, Inc.
Song, Y., and Ermon, S. (2020). Improved Techniques for Training Score-Based Generative Models. In Advances in neural information processing systems,Vol. 33.
Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., and Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. In International conference on learning representations.
Tzen, B., and Raginsky, M. (2019). Neural Stochastic Differential Equations: Deep Latent Gaussian Models in the Diffusion Limit.
Vahdat, A., Kreis, K., and Kautz, J. (2021). Score-based Generative Modeling in Latent Space. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, and J. W. Vaughan, editors, Advances in neural information processing systems,Vol. 34, pages 11287–11302. Curran Associates, Inc.
Xiao, Z., Kreis, K., and Vahdat, A. (2022). Tackling the generative learning trilemma with denoising diffusion GANs. In International conference on learning representations.
Yang, L., Zhang, Z., Song, Y., Hong, S., Xu, R., Zhao, Y., … Yang, M.-H. (2023). Diffusion models: A comprehensive survey of methods and applications. ACM Comput. Surv., 56(4).
Yuan, C. (2024). Diffusion models from scratch, from a new theoretical perspective.
Zhang, Q., and Chen, Y. (2023). Fast sampling of diffusion models with exponential integrator. In The eleventh international conference on learning representations.
Footnotes
エネルギー関数とスコア関数，どっちを学習の中心に据えるかについては (Salimans and Ho, 2021) も参照．↩︎
“Our sampling strategy is inspired by simulated annealing (Kirkpartick et al., 1983), (Neal, 2001) which heuristically improves optimization for multimodal landscapes.” (Y. Song and Ermon, 2019, p. 2) より．↩︎
DNS も SSM も使用可能であるが，ここでは Langevin サンプラーのアニーリングのために，ノイズが印加されたベクトル場 \(s_\theta(x,\sigma)\) の学習が必要であるため，DNS の選択が自然である (Y. Song and Ermon, 2019)．↩︎
これが可能であることは (Ho et al., 2020, p. 8) でも触れられている．↩︎
ちょうど，Neural ODE がタイムステップの取り方を適応的にしてくれたように．↩︎
ちょうど，MCMC がベクトル場に関する決定論的なフローで効率化させられるように．↩︎
(J. Song et al., 2021) 内では \(q_\sigma(x_t|x_{t-1},x_0)\) の形を与えていないが，Bayes の定理を通じてわかる：\[q_\sigma(x_t|x_{t-1},x_0)=\frac{q_\sigma(x_{t-1}|x_t,x_0)q_\sigma(x_t|x_0)}{q_\sigma(x_{t-1}|x_0)}.\]↩︎