brms を用いたベイズロジスティック回帰分析

概要

ロジスティック回帰分析は離散的な応答データを扱うことのできる一般化線型モデルである．他にも，高度に非線型な関係が予期される場合，ノンパラメトリック手法に移る前の簡単な非線型解析としても活躍する．本稿では BMI と LDL の非線型関係に関する探索的手法として，順序ロジスティック回帰分析を実行する．

1 はじめに

多くの社会的なデータは非数値的である．しかしその背後には潜在的な連続変数を想定することが多い．

加えて，線型回帰分析の結果複雑な非線型関係が予期された際，本格的なノンパラメトリック推論に移る前に，離散変数の設定に換言して非線型性を扱いやすくするなど，離散変数を扱う積極的理由もある．

本稿ではロジスティック回帰を主に扱う．

2 多項ロジスティック回帰

2.1 はじめに

ここでは BMI と LDL コレステロールの関係を見る．

2.1.1 BMI と LDL の関係

一般に HDL コレステロールは BMI と正の相関がある（特に２型糖尿病患者では (Hussain et al., 2019)）．

cor(raw_df$BMI, raw_df$HDL)

[1] -0.3689261

一方で LDL コレステロールと BMI の相関は弱い：

cor(raw_df$BMI, raw_df$LDL)

[1] 0.158966

しかし全く無関係ではないように見える：

boxplot(
  raw_df$LDL ~ raw_df$obesity,
  col = c("pink", "lightgreen", "skyblue"),
  main = "LDL classified by BMI",
  xlab = "BMI",
  ylab = "LDL"
)

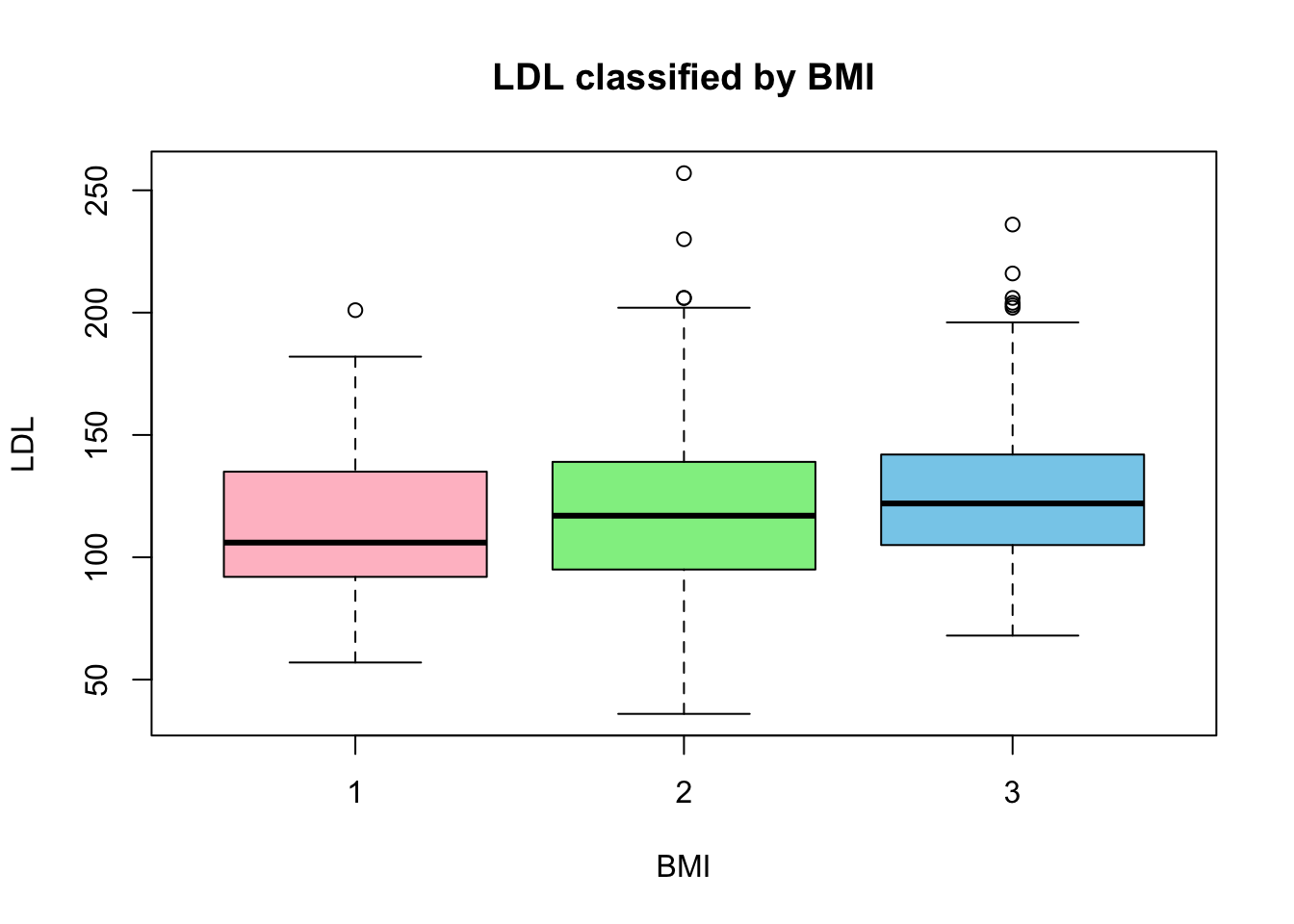
これは LDL と BMI の関係は非線型性が高く，その非線型関係が男女，さらに年齢で違うためかもしれない (Li et al., 2021)．

この関係を詳しく見ていくことで何か発見があるかもしれないだろう．

2.1.2 LAB

LAB (Inoue et al., 2010) は酸化変性した LDL のことで，別名超悪玉コレステロールと知られる．LDL コレステロールよりも動脈硬化リスクを（特に残余リスクとして）反映する新しいバイオマーカーになり得ると期待されている (Okamura et al., 2013)．

LAB と LDL の相関は高くない：

cor(raw_df$BMI, raw_df$LAB)

[1] 0.1952133

boxplot(
  raw_df$LAB ~ raw_df$obesity,
  col = c("gray", "pink", "skyblue"),
  main = "LAB classified by BMI",
  xlab = "BMI",
  ylab = "LAB"
)

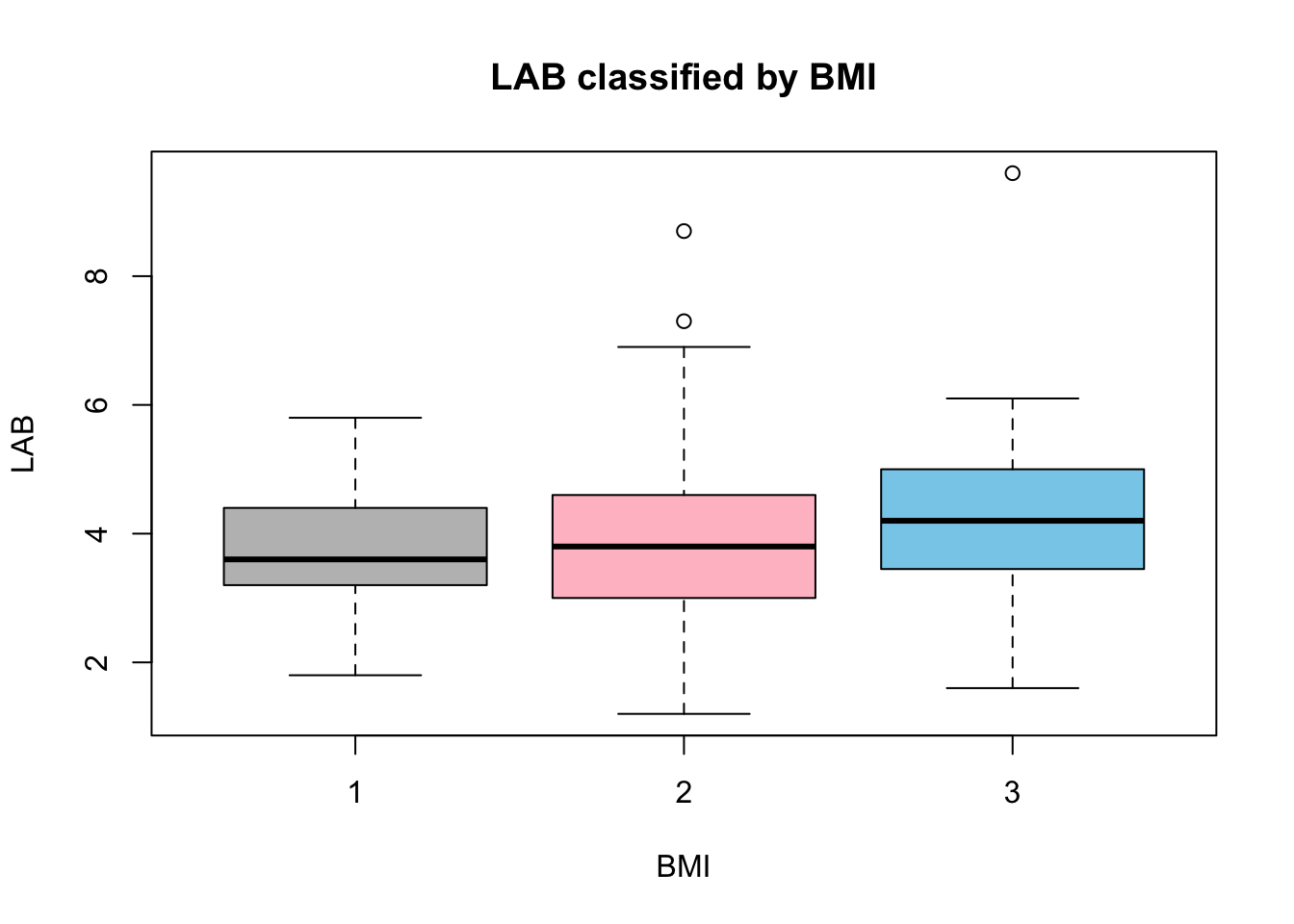
ここでは LAB と LDL の BMI への影響を比較したい．

2.1.3 BMI の離散化

BMI と LDL の関数関係は非線型性が予期される (Li et al., 2021)．

そこで BMI を直接被説明変数とするのではなく，離散化した順序変数 obesity を導入する：

raw_df <- raw_df %>%
  mutate(obesity = case_when(
  BMI < 18.5 ~ 1,  # underweight
  BMI < 25 ~ 2,    # normal
  BMI >= 25 ~ 3    # obese
  ))

2.2 LDL の予測力

LDL を直接用いて推定すると係数が極めて小さくなるため，対数変換によりスケールを変換して説明変数に入れる：

\[ \operatorname{P}[\texttt{obesity}>1]=g^{-1}(\beta_{\texttt{LDL}}\cdot\log(\texttt{LDL})-c_1) \] \[ \operatorname{P}[\texttt{obesity}>2]=g^{-1}(\beta_{\texttt{LDL}}\cdot\log(\texttt{LDL})-c_2) \]

formula_LDL <- bf(
  obesity ~ log(LDL),
  family = cumulative(link = "logit")
)
# prior_LDL <- prior(normal(0,0.1), class = b, coef = "logLDL")
fit_LDL <- brm(
  formula_LDL,
  data = raw_df,
  chains = 4, cores = 4
#  prior = prior_LDL
)

summary(fit_LDL)

 Family: cumulative 
  Links: mu = logit; disc = identity 
Formula: obesity ~ log(LDL) 
   Data: raw_df (Number of observations: 839) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Regression Coefficients:
             Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept[1]     2.05      1.26    -0.42     4.52 1.00     2671     2228
Intercept[2]     5.62      1.27     3.12     8.12 1.00     2606     2280
logLDL           0.97      0.27     0.46     1.50 1.00     2622     2226

Further Distributional Parameters:
     Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
disc     1.00      0.00     1.00     1.00   NA       NA       NA

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

LDL が上がるごとに，normal や underweight から obese に移る確率が上がるのが見える．

conditional_effects(fit_LDL, "LDL", categorical = TRUE)

prior_summary(fit_LDL)

                prior     class   coef group resp dpar nlpar lb ub       source
               (flat)         b                                         default
               (flat)         b logLDL                             (vectorized)
 student_t(3, 0, 2.5) Intercept                                         default
 student_t(3, 0, 2.5) Intercept      1                             (vectorized)
 student_t(3, 0, 2.5) Intercept      2                             (vectorized)

\(c_1,c_2\) には \(0\) を中心とした \(t\)-事前分布が置かれているため，識別性は保たれると考えて良い．

2.3 LAB との比較

実は LDL よりも LAB の方が少し予測力が高い．しかも LAB は \([1,10]\) に値を取るので，対数変換をするよりも平方根変換をする方が自然である：

formula_LAB <- bf(
  obesity ~ sqrt(LAB),
  family = cumulative(link = "logit")
)
fit_LAB <- brm(
  formula_LAB,
  data = raw_df,
  chains = 4, cores = 4
)

loo_compare(loo(fit_LDL), loo(fit_LAB))

        elpd_diff se_diff
fit_LAB  0.0       0.0   
fit_LDL -2.2       3.9

conditional_effects(fit_LAB, "LAB", categorical = TRUE)

LAB が上昇すると underweight, normal から obese に移る確率がグンと上がるのが見える．

2.4 双方の採用

前節で LAB と LDL を比較すると，前者のみを用いたモデルの方が予測力が高いことを見た．

では両方をモデルに入れてベイズ推論をすることで，２つの情報を統合したより良いモデルができるだろうか？

df_double <- data.frame(
  obesity = raw_df$obesity,
  z_sqrt_LAB = scale(sqrt(raw_df$LAB)),
  z_log_LDL = scale(log(raw_df$LDL))
)
formula_double <- bf(
  obesity ~ z_sqrt_LAB + z_log_LDL,
  family = cumulative(link = "logit")
)
fit_double <- brm(
  formula_double,
  data = df_double,
  chains = 4, cores = 4
)

実際予測性能の面では両方入れたモデルの方が良いようである：

loo_compare(loo(fit_LAB), loo(fit_double))

           elpd_diff se_diff
fit_double  0.0       0.0   
fit_LAB    -0.3       1.7

plot(fit_double, variable = c("b_z_sqrt_LAB", "b_z_log_LDL"))

LDL の方が僅かに縮小されて推定されていることがわかる．

さらには LAB と LDL がモデルに入っている確率を出す方法は別稿で追求する：

ベイズ変数選択

BMI データの重線型回帰を題材として

2024-12-10

2.5 交絡の存在

formula_double_confound <- bf(
  obesity ~ z_sqrt_LAB * z_log_LDL,
  family = cumulative(link = "logit")
)
fit_double_confound <- brm(
  formula_double_confound,
  data = df_double,
  chains = 4, cores = 4
)

plot(fit_double_confound, variable = c("b_z_sqrt_LAB", "b_z_log_LDL", "b_z_sqrt_LAB:z_log_LDL"))

若干の交絡の存在が疑われる．LDL が大きいほど，LAB と BMI との関係は減少していき，逆もまた然りである．

これは共線型性が強いので当然とも思われる：

cor(df_double$z_sqrt_LAB, df_double$z_log_LDL)

[1] 0.5204453

しかし必ずしも条件数が大きいわけではない．

X <- model.matrix(~ z_sqrt_LAB + z_log_LDL, data = df_double)
kappa(X)

[1] 1.879479

2.6 名目モデルを使ってしまったら？

underweight, normal, obese 間の順序構造を無視して，カテゴリカル分布を通じてモデリングをしても，実は当てはまりは必ずしも悪くない．

formula_nominal <- bf(
  obesity ~ LAB,
  family = categorical(link = "logit")
)
fit_nominal <- brm(
  formula_nominal,
  data = raw_df,
  chains = 4, cores = 4
)

waic(fit_LAB)


Computed from 4000 by 839 log-likelihood matrix.

          Estimate   SE
elpd_waic   -686.0 18.5
p_waic         2.8  0.1
waic        1372.0 37.0

waic(fit_nominal)


Computed from 4000 by 839 log-likelihood matrix.

          Estimate   SE
elpd_waic   -685.8 18.6
p_waic         3.7  0.2
waic        1371.6 37.2

ほとんど質的には一致した結果を得る：

conditional_effects(fit_nominal, "LAB", categorical = TRUE)

ひょっとしたら，BMI を離散化したという点で順序変数に思えるかもしれないが，これは単なる思い込みで，「痩せている」ことと「太っている」ことに順序関係を仮定することはむしろノイズになっているのかもしれない．

2.7 非線型関係の追求

`brms` を用いたノンパラメトリック回帰分析

BMI データを題材として

2024-12-16

2.8 共変量の追加と効果の観察

raw_df$sqrt_LAB <- sqrt(raw_df$LAB)
raw_df$log_Age <- log(raw_df$Age)
formula_LAB_cov <- bf(
  obesity ~ log_Age + SEX + log_Age:SEX + (0 + SEX | sqrt_LAB),
  family = categorical(link = "logit")
)
fit_LAB_cov <- brm(
  formula_LAB_cov,
  data = raw_df,
  chains = 4, cores = 4
)

summary(fit_LAB_cov)

 Family: categorical 
  Links: mu2 = logit; mu3 = logit 
Formula: obesity ~ log_Age + SEX + log_Age:SEX + (0 + SEX | sqrt_LAB) 
   Data: raw_df (Number of observations: 839) 
  Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup draws = 4000

Multilevel Hyperparameters:
~sqrt_LAB (Number of levels: 56) 
                               Estimate Est.Error l-95% CI u-95% CI Rhat
sd(mu2_SEXfemale)                  0.20      0.14     0.01     0.54 1.00
sd(mu2_SEXmale)                    0.20      0.14     0.01     0.53 1.00
sd(mu3_SEXfemale)                  0.48      0.23     0.05     0.94 1.01
sd(mu3_SEXmale)                    0.28      0.19     0.01     0.70 1.00
cor(mu2_SEXfemale,mu2_SEXmale)    -0.12      0.57    -0.97     0.92 1.00
cor(mu3_SEXfemale,mu3_SEXmale)    -0.10      0.54    -0.96     0.90 1.00
                               Bulk_ESS Tail_ESS
sd(mu2_SEXfemale)                  1288     1735
sd(mu2_SEXmale)                    1118     1308
sd(mu3_SEXfemale)                   792      963
sd(mu3_SEXmale)                    1027     1614
cor(mu2_SEXfemale,mu2_SEXmale)     2097     2182
cor(mu3_SEXfemale,mu3_SEXmale)     1638     1708

Regression Coefficients:
                    Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
mu2_Intercept          -4.06      1.92    -7.89    -0.26 1.00     2108     2674
mu3_Intercept          -6.39      2.35   -11.05    -1.71 1.00     2049     2334
mu2_log_Age             1.55      0.50     0.55     2.56 1.00     2069     2656
mu2_SEXmale            12.79      5.40     2.66    24.16 1.00      994     1566
mu2_log_Age:SEXmale    -2.98      1.34    -5.79    -0.43 1.00     1004     1534
mu3_log_Age             1.81      0.61     0.63     3.02 1.00     2028     2315
mu3_SEXmale            14.91      5.62     4.64    26.55 1.00      933     1490
mu3_log_Age:SEXmale    -3.31      1.40    -6.16    -0.73 1.00      945     1525

Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).

conditional_effects(fit_LAB_cov, "SEX", categorical = TRUE)

一般に男性の方が太っている確率が高くなる．これはよく知られているようである．

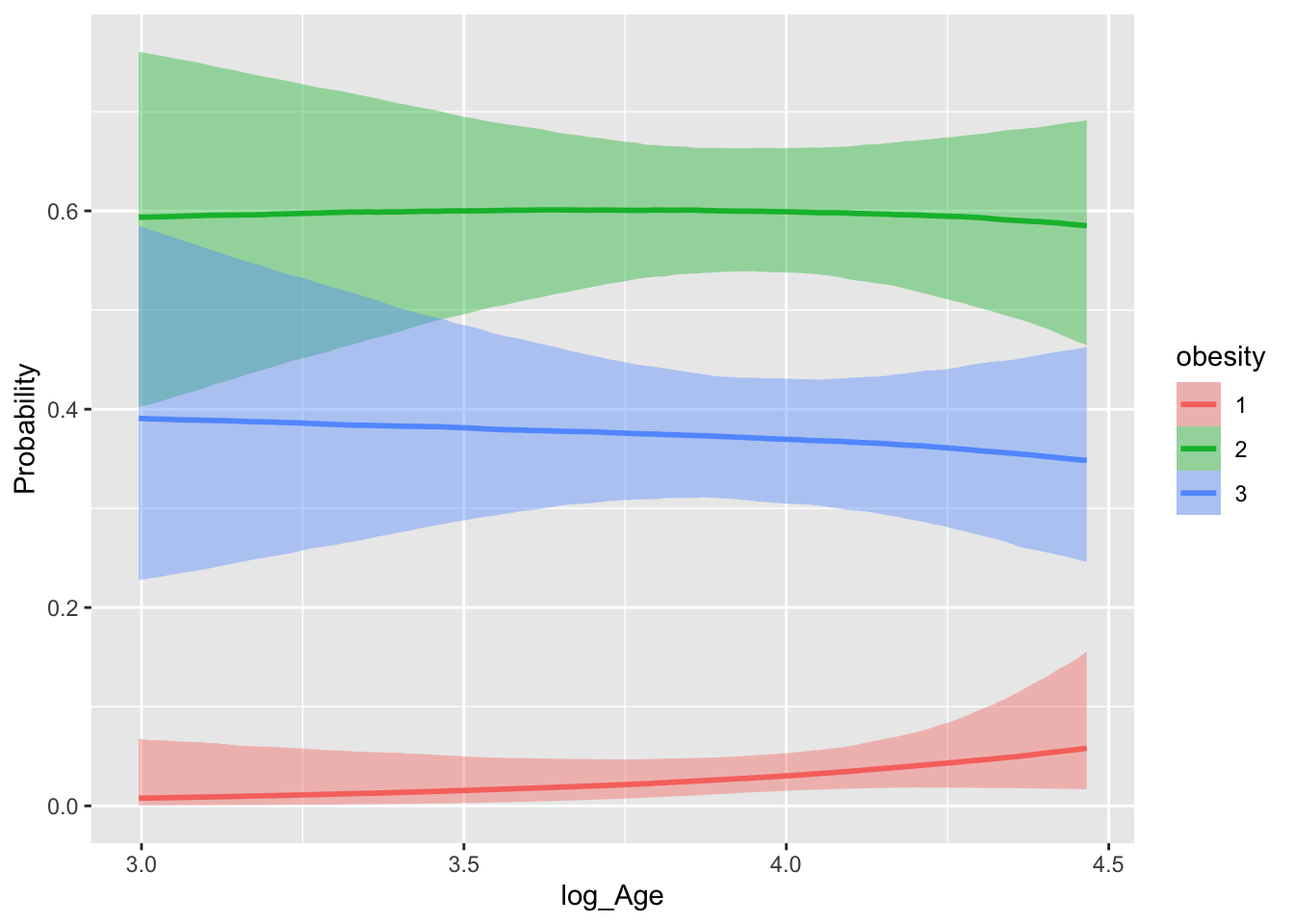
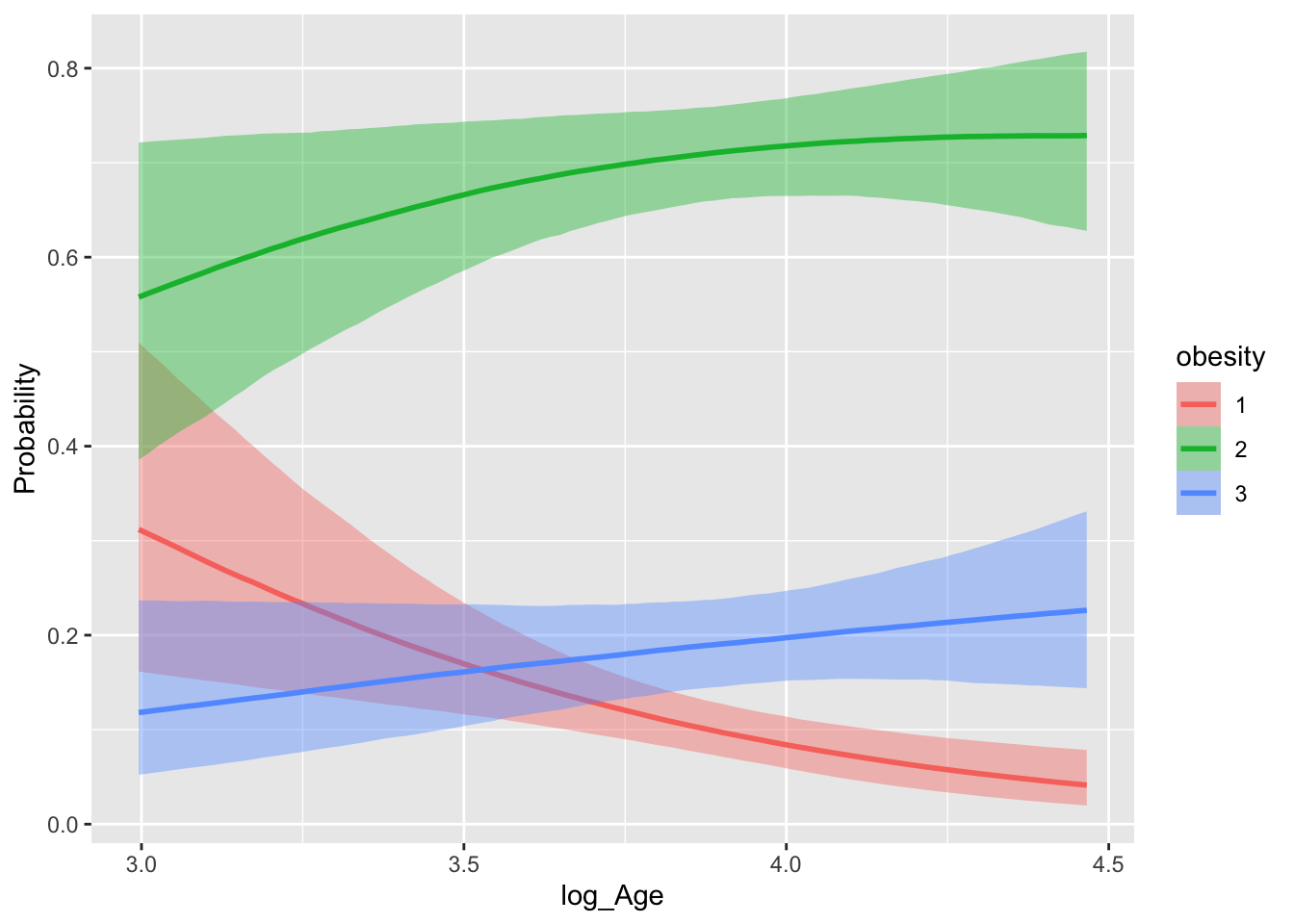
conditional_effects(fit_LAB_cov, "log_Age", conditions = list(SEX = "male"), categorical = TRUE)

conditional_effects(fit_LAB_cov, "log_Age", conditions = list(SEX = "female"), categorical = TRUE)

女性は年齢とともに太る傾向が見えるが，男性はそうでもない（むしろ逆である）ようである．

そして共変量を追加したことでモデルの予測力が大きく良くなっている：

loo_compare(loo(fit_LAB), loo(fit_LAB_cov))

Warning: Not all models have the same y variable. ('yhash' attributes do not
match)

            elpd_diff se_diff
fit_LAB_cov   0.0       0.0  
fit_LAB     -11.2       8.1

pp_check(fit_LAB_cov)

Using 10 posterior draws for ppc type 'dens_overlay' by default.

2.9 その他の共変量の探索

BMI と LDL は，骨ミネラル密度 (BMD: Bone Mineral Density) に因果的な影響を与えることが知られている (Wu, 2024)．

P1NP は骨形成マーカー，ALP は骨の形成や骨疾患の評価に役立つ酵素である．

deoxypyridinolin (DPD) は骨を構成するⅠ型コラーゲンを束ねる蛋白質で、骨吸収の指標になる．

他に Ca, Mg などの値もある．

3 階層ロジットモデル

3.1 はじめに

データの不均衡性に着想を得て，「太っているかいないか？」の後に「痩せ気味かどうか？」という２つのロジット回帰の連続とみることを考える．

raw_df <- raw_df %>%
  mutate(obesity_former = case_when(
  BMI < 25 ~ 0,    # normal
  BMI >= 25 ~ 1    # obese
  ))
raw_df <- raw_df %>%
  mutate(obesity_latter = case_when(
  BMI < 18.5 ~ 0,    # underweight
  BMI >= 18.5 ~ 1    # normal
  ))

formula_former <- bf(
  obesity_former ~ LAB,
  family = bernoulli(link = "logit")
)
fit_former <- brm(
  formula_former,
  data = raw_df,
  chains = 4, cores = 4
)
formula_latter <- bf(
  obesity_latter ~ LAB,
  family = bernoulli(link = "logit")
)
fit_latter <- brm(
  formula_latter,
  data = raw_df,
  chains = 4, cores = 4
)

References

Hussain, A., Ali, iftikhar, Kaleem, W. A., and Yasmeen, F. (2019). Correlation between body mass index and lipid profile in patients with type 2 diabetes attending a tertiary care hospital in peshawar: Correlation between BMI & lipid profile in patients with T2DM. Pakistan Journal of Medical Sciences, 35(3).

Inoue, N., Okamura, T., Kokubo, Y., Fujita, Y., Sato, Y., Nakanishi, M., … Sawamura, T. (2010). LOX index, a novel predictive biochemical marker for coronary heart disease and stroke. Clinical Chemistry, 56(4), 550–558.

Li, H., Ma, J., Zheng, D., Li, X., Guo, X., Wang, J., and Su, P. (2021). Sex differences in the non-linear association between BMI and LDL cholesterol in middle-aged and older adults: Findings from two nationally representative surveys in china. Lipids in Health and Disease, 20(1), 162.

Okamura, T., Sekikawa, A., Sawamura, T., Kadowaki, T., Barinas-Mitchell, E., Mackey, R. H., … Ueshima, H. (2013). LOX-1 ligands containing apolipoprotein b and carotid intima-media thickness in middle-aged community-dwelling US caucasian and japanese men. Atherosclerosis, 229(1), 240–245. doi: 10.1016/j.atherosclerosis.2013.04.023.

Wu, W. A. C., Yuxiang AND Ma. (2024). Causal relationships between body mass index, low-density lipoprotein and bone mineral density: Univariable and multivariable mendelian randomization. PLOS ONE, 19(6), 1–14.