ベイズ変数選択

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1 はじめに

1.1 （復習）ベイズデータ解析の第一歩

データの非線型変換も取り入れたベイズ線型重回帰分析は，多くの場合，データを理解するための最初の解析手法として選択される．

その方法を brms パッケージを用いて実践したのが次の記事である：

前稿では BMI を LAB と LDL から予測する問題を，線型回帰モデルから始めた．

交差項を追加することで，LDL が違う群に対して LAB がどう変わるかの層別の違いを見ることができる．

事後予測分布によるモデルのチェックは残差プロットと同様に，極めて手軽かつ有力なモデル検証の方法である．

これにより関数関係の非線型性が疑われたため，被説明変数 BMI に対して対数変換を施して線型回帰をすると，予測性能の改善が見られた．

事後予測分布のプロットだけでなく，その「よさ」の定量的な指標として交差検証による事後予測スコア elpd (Vehtari et al., 2017) があることを学んだ．

1.2 ベイズから見た変数選択

こうして予測力を基にモデル選択をする方法は得たわけであるが，純粋にベイズ的な観点から変数選択を行う方法が大きく分けて２つある．

1.2.1 縮小事前分布による方法

１つ目が「モデルに含まれる変数は少ないはずである」という信念を表現した事前分布を用いる方法である（第 2 節）．

これは馬蹄事前分布 (Carvalho et al., 2009), (Carvalho et al., 2010)，Laplace 事前分布 / Bayesian Lasso (Park and Casella, 2008) などの global-local shrinkage prior を用いる方法である．

この方法は点推定や頻度論的な方法ではほとんど唯一の変数選択の方法であり，正則化またはスパース性 のキーワードの下で盛んに研究されている (Hastie et al., 2015)．

1.2.2 ベイズ変数選択

２つ目が spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) という \(0\) にマスを持つ事前分布を用いる方法である： \[ p(dx)=\prod_{i=1}^d\biggr(\omega_i\phi_i(x_i)\,dx_i+(1-\omega_i)\delta_0(dx_i)\biggl) \tag{1}\]

この方法では当該変数の 事後包含確率 (PIP: Posterior Inclusion Probability) を導出することができる．実際 (1) は混合分布の形をしており，spike \(\delta_0\) と slab \(\phi_i\) のどちらからサンプリングされるかを表す潜在変数 \(\gamma_i\in\{0,1\}\) を導入すれば，\(\operatorname{P}[\gamma=0|\mathcal{D}]\) という事後確率こそが変数 \(x_i\) がモデルに入る事後確率である．

PIP を用いることで「当該変数がモデルに含まれるか？」という問題に直接ベイズ的に答えることができる．これを ベイズ変数選択 という 3．

一方で前述の global-local shrinkage prior でも，post-processing を通じて同様に PIP を近似的に算出することができる (Hahn and Carvalho, 2015)．

1.3 ベイズモデル平均を見据えて

このようにベイズ変数選択 1.2.2 では，変数選択も統計的推論の問題として解く．

この方法は最適なレートで縮小する効果を持ち (Castillo et al., 2015)，また予測力にも優れる (Porwal and Raftery, 2022)．

最終的には，適切に構造と事前分布が設定されたベイズモデルを用いて，ベイズ推論により変数の関連度を自動で判断して結果を出すことが理想である．その意味では全ての変数を（適切に）入れたモデルを用いることが好ましい．¹

ベイズ変数選択はこの最終目標に向かうまでの探索的な中途解析と見ることもできる．

実際，ベイズ変数選択により得た事後包含確率 PIP は，ベイズモデル平均 (BMA: Bayesian Model Averaging) (Hoeting et al., 1999) に用いることができる．

変数選択・モデル選択を実行し，選ばれた単一のモデルで推論・予測を実行するよりも，尤度が必ずしも最も高いわけではないモデルも捨てずに推論に用いることで精度を上げることができる．

これがベイズモデル平均の考え方であり，ベイズの美点をフルに発揮する枠組みであると言える．実際，(Porwal and Raftery, 2022) では線型回帰モデルの変数選択において，３つの適応的 BMA 手法が全てのタスクでベストな予測性能を示したことを報告している．

2 縮小事前分布による方法

2.1 多くの説明変数が存在する場合の事前分布

stan_glm では回帰係数には適切な分散を持った独立な正規分布（\(g\)-prior）をデフォルトの事前分布としている．

brms では一様事前分布である．

仮に説明変数が極めて多い場合，このデフォルト事前分布を採用し続けることは適切ではない．

実際，独立な正規・一様分布に従う説明変数が大量にある場合，これは「ベイズ（事後平均）推定量の分散が大きい」という事前分布を採用していることに含意してしまう．

仮に \(\sigma\) にも同様の分散の大きい事前分布をおいているのならば辻褄は合うが，そうでないならばベイズ決定係数 \(R^2\) にほとんど \(1\) 近くの事前分布をおいていることに等価である．

すなわち過学習されたモデルに強い事前分布をおいていることになる (Gelman et al., 2020, p. 208)．これは我々の信念と食い違うだろう．そもそも弱情報であるべきデフォルト事前分布としては相応しくない．

2.2 縮小事前分布

まずは各変数の正規事前分布の分散を十分小さくして，誤差 \(\epsilon\) の分散 \(\sigma^2\) のスケールと同一にすることが考えられる．

この際 \(R^2\) にはほとんど無情報な事前分布が仮定されるのと同一である．

さらに，仮に「多くの説明変数のうち，一部しか重要なものはなく，他の大部分はほとんど無関係である」と思っている，あるいは思いたいとする．変数選択を行いたい場合がこれにあたる．

この信念を正確に表現する事前分布の一つに馬蹄事前分布 (horseshoe prior) (Carvalho et al., 2009), (Carvalho et al., 2010) とその正則化バージョン (Piironen and Vehtari, 2017b) がある．

これらの分布は global-local shrinkage prior と呼ばれ，\(R^2\) 上の事前分布に，\(0\) 上にスパイクを生じさせる．モデルに支持されない説明変数の係数を \(0\) に向かって縮小する効果があり，結果としてシンプルなモデルを選好することになる．

Stan においては prior=hs によって指定できる (Gelman et al., 2020, p. 209)．

2.3 Local Scale Mixture

多くの正則化事前分布は次のような正規分布の local scale mixture (West, 1987) の形をしている：² \[ \pi(\beta_j|\lambda)=\int_\mathbb{R}\phi(\beta_j|0,\lambda^2\lambda^2_j)\pi(\lambda_j^2)\,d\lambda_j. \]

\(\pi\) が２点のみに台を持つ場合が spike-and-slab (1) であった (Polson and Scott, 2011)．SSVS （第 3.2 節）も含む．\(\pi\) が絶対連続である場合も次のような例を持つ (Polson and Scott, 2012)：

• 二重指数分布 (double exponential) / Bayesian Lasso (Park and Casella, 2008), (Hans, 2009)
• 馬蹄事前分布 (horseshoe prior) (Carvalho et al., 2009), (Carvalho et al., 2010)
• Bayesian elastic net (Hans, 2011)

(Ishwaran and Rao, 2005) はこれらの研究より早い段階で，\(\pi\) に \(0\) の近くと \(0\) から大きく離れた二峰を持つ分布を用意している．

2.4 ベイズ縮小の効果

スケールパラメータ \(\lambda\) は，LASSO (Tibshirani, 1996) では CV などの基準により選択することになるが，\(\lambda\) を推定してモデル平均を行うことでより高い推定精度を得ることができる (Hans, 2009)．

同様にして事後平均推定量により推定精度は改善されるが，ほとんど確実にこれはスパースではない．従って推定量のスパース性と推定精度はトレードオフの関係にあり，完全にベイジアンに Bayesian LASSO を実行すると本末転倒に陥るという一面もある．

このためベイズ縮小事前分布を用いた場合，自動的にスパース性に基づいたモデル選択ができるというわけではなく，事後モデル確率 (posterior model probability) を最大にするものを見つけるという post-processing が必要になる (Section 1.5 Hahn and Carvalho, 2015, p. 438), (Piironen et al., 2020), (Jim E. Griffin, 2024)．

しかし以上のベイズモデル選択の手続きを踏むことによって，事後モデル確率を最大にするものという統計的・決定理論的に根拠を持ったモデル選択を実行することができる．

LASSO はベイズモデル選択の結果よりも予測性能が必ずしも高いわけではないにも拘らず，より多くの変数をモデルに残しがちであることも報告されている (Porwal and Raftery, 2022, p. 3)．これは馬蹄事前分布などの最新の縮小事前分布は，回帰係数の効果量やモデルの大きさなどに応じて適応的に正則化の強さを加減しているためだとも言える (Li et al., 2023)．

2.5 馬蹄事前分布

馬蹄事前分布 \[ \beta_j|\lambda_j,\tau\sim\mathrm{N}(0,\lambda_j^2\tau^2),\qquad\lambda_j\sim\operatorname{half-Cauchy}(0,1), \] は global-local shrinkage prior の１つである．

というのも，hyperparameter \(\tau\) で決まる大域的な縮小効果がある一方で，半 Cauchy 分布による混合の構造が局所的なスケールパラメータ \(\lambda_j\) を調整し，縮小される変数とされない変数とにコントラストをつけてくれる．

つまり，馬蹄事前分布は「少数の変数のみが大きなスケールを持つ」という信念を，階層的な構造で表現したものと理解できる．

最後の問題はハイパーパラメータ \(\tau\) の調整である．

交差検証法や周辺尤度の値，情報量規準により \(\tau\) の値を選んで推定を実行することもできる（経験ベイズ）．(Polson and Scott, 2011) では \[ \tau|\sigma\sim\operatorname{half-Cauchy}(0,\sigma^2) \] という hyperprior を推奨している．ただし \(\sigma^2\) は誤差の分散と共通とする．一方で (Piironen and Vehtari, 2017a) は事前の信念から非零の係数を持つべき変数の数 \(p_0\) に対して \[ \tau|\sigma\sim\operatorname{half-Cauchy}(0,\tau^2_0),\qquad\tau_0:=\frac{p_0}{p-p_0}\frac{\sigma^2}{\sqrt{n}}, \] により hyperprior を置くことを推奨している．

2.6 正則化

馬蹄事前分布はモデルに支持される変数の係数はほとんど縮小させないように設計されている．これは美点である一方で，正則化の効果を弱めてしまい，縮小事前分布であるはずが推定の安定化が望めない場合がある．

例えばロジスティック回帰に馬蹄事前分布をおくと，分離 などが起こって識別性が弱い場合に Cauchy 分布と同様の裾を持つために事後平均推定量が存在しなくなってしまう (Ghosh et al., 2018)．

また従来の馬蹄事前分布では，ときに事後分布が漏斗型を持ってしまい，収束が劇的に遅くなるという現象も観測されていた (Piironen and Vehtari, 2015)．

これらの問題を解決するために spike-and-slab 事前分布の slab width と同様の正則化ハイパーパラメータ \(c>0\) を導入した 正則化馬蹄事前分布 (regularized horseshoe prior) (Piironen and Vehtari, 2017b) が提案されている： \[ \beta_j|\lambda_j,\tau,c\sim\mathrm{N}(0,\tau^2\widetilde{\lambda}_j^2),\qquad\widetilde{\lambda}_j:=\frac{c^2\lambda_j^2}{c^2+\tau^2\lambda_j^2},\lambda_j\sim\operatorname{half-Cauchy}(0,1). \] \(c\to\infty\) の極限では馬蹄事前分布に一致する．この \(c\) には次の hyperprior を推奨している： \[ c^2\sim\operatorname{Inv-Gamma}(\nu/2,\nu s^2/2). \] これにより最大の係数に対して \(t_\nu(0,s^2)\) の事前分布を置くことに等価になる ((2.11) Piironen and Vehtari, 2017b, p. 5025)．

2.7 rstanarm での利用

rstanarm では hs (hierarchical shrinkage) 事前分布

hs(df = 1, global_df = 1, global_scale = 0.01, slab_df = 4, slab_scale = 2.5)

が利用可能である．これは \[ \tau|\sigma\sim\operatorname{half-t}(\textcolor{purple}{\mathtt{global_df}}),\qquad\lambda_j\sim\operatorname{half-t}(\textcolor{purple}{\mathtt{df}}) \] というものであるから，df=1, global_df=1 が正則化馬蹄事前分布に対応する．

global_scale が \(\tau_0\) に，slab_scale が \(s\)，slab_df が \(\nu\) に対応する．

3 ベイズ変数選択

3.1 はじめに：階層モデリング

ベイズ変数選択 では，説明変数 \(\{x_i\}_{i=1}^p\) のそれぞれがモデルに含まれるかを意味する潜在変数 \(\{\gamma_i\}_{i=1}^p\in\{0,1\}^p=:\Gamma\) の事後分布を算出して，特定の変数がモデルに含まれる確率を算出する．

最終的にこの確率分布は，ベイズモデル平均 (BMA: Bayesian Model Averaging) と言って，それぞれのモデルの事後予測を平均するためのプライヤーとして用いることもできる．

この方法では \[ p(\gamma)=\prod_{i=1}^p\omega_i^{\gamma_i}(1-\omega_i)^{1-\gamma_i},\qquad p(\sigma^2)\,\propto\,\sigma^{-2} \] \[ p(\beta|\sigma,\gamma)\,d\beta=\mathrm{N}_p(0,\Sigma(\sigma,\gamma)) \] という階層構造を通じて，回帰モデルに潜在変数 \(\gamma\) を導入する．\(\Sigma\) は (X. Liang et al., 2022) では独立，(George and McCulloch, 1997) では \(g\)-prior とする： \[ \Sigma(\sigma,\gamma):=g\sigma^2(X^\top_\gamma X_\gamma)^{-1}. \] \(g\) は global scale parameter と呼ばれ，これにさらに hyperprior を設定することもある (F. Liang et al., 2008), (Ley and Steel, 2009)．

このアプローチは (George and McCulloch, 1997) らによって創始された．（仮に \(p\) が比例的に増えるとしても） \(n\to\infty\) の極限で PIP は正しいモデル上の Delta 測度に収束する (Shang and Clayton, 2011)．

3.2 確率的探索法

特に (George and McCulloch, 1993) では \[ \beta_i|\gamma_i\sim(1-\gamma_i)\mathrm{N}(0,\sigma_i^2)+\gamma_i\mathrm{N}(0,c_i^2\sigma_i^2) \tag{2}\] という構造を設定し，データ拡張に基づく Gibbs サンプラーによって推定することを提案した．

この方法は 確率的探索法 (SSVS: Stochastic Search Variable Selection) と呼ばれる．³

しかし (2) は spike-and-slab (1) の近似になっているため，\(\gamma_i=1\) の事後確率は正確に PIP になっているわけではない．

この近似は Gibbs サンプラーを高速にするという利点はあったかもしれないが，現代では spike-and-slab (1) に直接適用できる高速なサンプラーが多数開発されている．

3.3 Add-Delete-Swap による探索

計量化学 (chemometrics) では \(p\) が特に高次元になり得る．(Brown et al., 1998) は近赤外線分光法で得られたデータから，予測に有用な波長を選択する問題に対処するためにベイズ変数選択の方法を用いることを考えた．

そのためにまず第 3.1 節の階層モデルを多次元化し，推定には乱歩 MH 法を用いた．

(Brown et al., 1998) の乱歩 MH 法の提案核は，Add-Delete-Swap の動きをするものであった：

次の２つの動きを，それぞれ確率 \(\phi,1-\phi\) で行う；

1. Adding or Deleting

   新たな変数 \(x_i\) をランダムに選び，まだモデルに入っていない場合は入れ，すでにモデルに含まれている場合は取り除く．

2. Swapping

   モデルに含まれていない変数 \(x_i\) と含まれている変数 \(x_j\) をそれぞれランダムに選び，入れ替える．

(Yang et al., 2016) は MH 法の計算複雑性を解析し，\(p\) が大きい場合にも計算量が線型にしか増加しない乱歩 MH 法を提案した．

3.4 超次元 MCMC による PIP 算出

事後包含確率を出すにあたって，Reversible-Jump MCMC (Green, 1995) などの超次元手法を用いることも考えられる．

超次元 MCMC とは，一般に複数のモデルから同時にサンプリングするための用いられ，ベイズ変数選択法は分解可能なグラフィカルモデルに対する超次元 MCMC 法の特別な場合と見れる (Godsill, 2001, p. 232)．

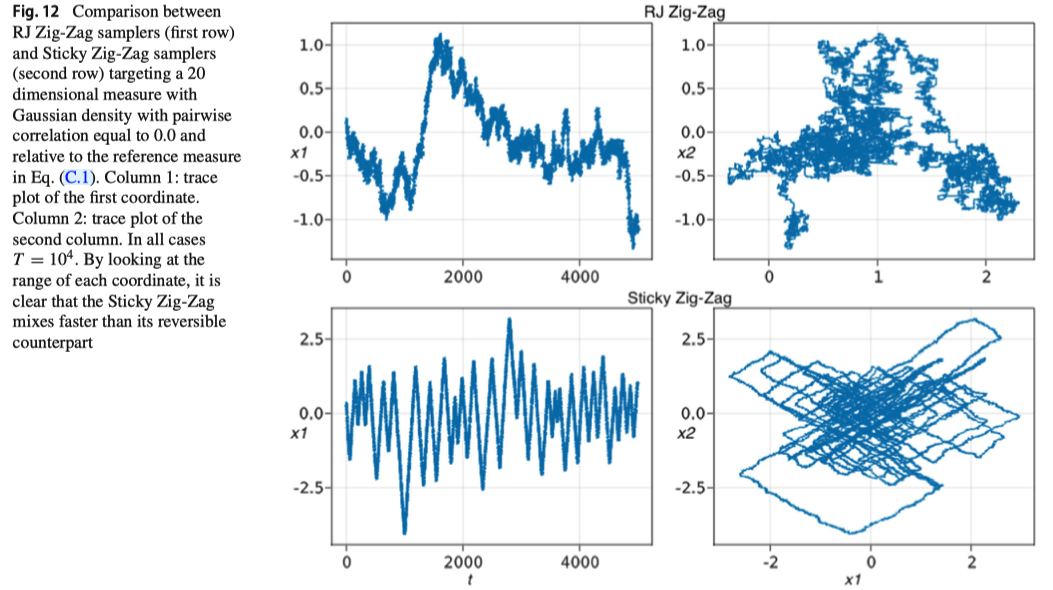
詳しくは別稿で取り上げるが，特に Sticky PDMP (Bierkens et al., 2023) は有力な PIP 算出法になる．

3.5 計算の問題

ベイズ変数選択とはモデル空間 \(\Gamma=\{0,1\}^p\) 上の事後分布を計算することであるが，これを効率的に行う MCMC を構成することが中心的な問題になる．

ここまで叙述してきた Gibbs サンプラー（例えば確率的探索法 3.2 など）は，\(p=2\) の極めて簡単な設定で簡単に崩壊する．というのも，２つの同等な説明力を持つ確率変数が強い相関を持つ場合，\((\beta,\gamma)\) の同時分布は強い二峰性を持つ．

その結果ただナイーブに Gibbs サンプラーを適用しただけでは片方の峰しか見つけることができず，PIP について偏った結果を出してしまう (Section 5.1 Zanella and Roberts, 2019)．

推定したいモデルが階層モデルである限り，多峰性の問題は常に付きものである．

\(p=2\) の時でさえ深刻になり得る多峰性の問題に加えて，共変量の数 \(p\) が大きい現代的な問題に対処する必要もあることを思えば，ベイズ変数選択の問題は，多峰性に強い効率的なベイズ計算法を開発するという普遍的な課題に回収されるのである．

3.6 Tempered Gibbs サンプラー

目標分布の条件付き分布 \(f(x_i|x_{-i})\) が多峰性を持つ場合，何らかの軟化 \(g(x_i|x_{-i})\) を考えることがあり得る．これに対して \[ p_i(x):=\frac{g(x_i|x_{-i})}{f(x_i|x_{-i})} \] と定め，まず \((p_1(x),\cdots,p_p(x))\) に従って \(i\in[p]\) を選び，続いて \(x_i\sim g(x_i|x_{-i})\) をサンプリングする random scan Gibbs サンプラーを考えると，これはやはり \(f\) を不変分布にもつ．

この方法では \(p_i(x)\) で各説明変数 \(x_i\) に傾斜をつけているために，特に PIP の高い \(i\in[p]\) から優先的にサンプリングすることができる．この方法は後述 3.7 節の informed MCMC の先駆けとなった．

3.7 Locally Informed MH Samplers

Add-Delete-Swap による乱歩 MH 法 3.3 の設計は，見通しの良い素朴な構成であるが，効率的な動きである保証は全くない．さらには \(\phi\) やそれぞれの候補を持ってくる確率など，ユーザーが調整する必要があるハイパーパラメータも多い．

対称かつ局所的なサンプラーの中では，採択率が高いほど効率が良い (Peskun, 1973), (Tierney, 1998)．そこで離散空間上の乱歩 MH 法の採択率を上げるために，現在位置の周囲の点の情報を収集して次の動きを決めるサンプラーが Informed MCMC の名前の下で開発されている (X. Liang et al., 2022, p. 84)．

多くの locally informed MCMC (Zanella, 2020) では，通常の乱歩 MH 核 \(Q\) を基底核 (base kernel) として，これを近傍での事後分布の様子を要約した 釣り合い関数 (balancing function) \(g\) を用いて修正することで効率的な動きを達成する： \[ q_g(\gamma,\gamma')\,\propto\,g\left(\frac{\pi(\gamma')}{\pi(\gamma)}\right)q(\gamma,\gamma'). \]

この中でも LIT (Locally Informed and Thresholded proposal) (Zhou et al., 2022) は釣り合い関数として閾値関数 (threshold function) \[ g(t)=p^L\land(p^l\lor t),\qquad-\infty<l<L<\infty. \] を用い，さらに提案核 \(Q\) を単なる一様分布ではなく第 3.3 節で考えられた Add-Delete-Swap 核 (Brown et al., 1998) にとることで，一定の条件の下で 次元 \(p\) に依存しない収束速度 を達成することを示した．

3.8 適応的なサンプラー

LIT は固定した基底核 \(Q\) を取り，そこから \(g\) で修正することを基本戦略としていた．一方でそもそも基底核 \(Q\) を適応的に調整していくメカニズムを導入することができる．

ASI (Adaptively Scaled Individual adaptation) (J. E. Griffin et al., 2021) では，(Brown et al., 1998) の Add-Delete-Swap 核 3.3 \[ q_\eta(\gamma,\gamma')=\prod_{j=1}^pq_{\eta,j}(\gamma_j,\gamma_j'),\qquad \eta=(A_1,\cdots,A_p,D_1,\cdots,D_p)\in(0,1)^{2p}, \] \[ q_{\eta,j}(0,1)=\eta_j=A_j,\qquad q_{\eta,j}(1,0)=\eta_{p+j}=D_j, \] を元にして，\(\eta=(A,D)\) を適応的に更新していくことを考える．その際の目安は，\(x_j\) の PIP \(\pi_j\) から定まる \[ A_j^\mathrm{opt}:=1\land\frac{\pi_j}{1-\pi_j},\qquad D_j^\mathrm{opt}:=1\land\frac{1-\pi_j}{\pi_j}, \] である．これの推定量 \(\eta^{(i)}\) を各段階で構成した上で，総じた採択率を調整する学習率のようなパラメータ \(\zeta^{(i)}\) も導入し，(Robbins and Monro, 1951) の方法で更新していく．

実は ASI は (X. Liang et al., 2023) がいう 確率近傍サンプラー (random neighbourhood sampler) の例になっている．これは Add-Delete-Swap (Brown et al., 1998) のように提案される近傍が，補助的な離散確率変数 \(k\in[K]\) によって定まるような乱歩 MH 法をいう．

(X. Liang et al., 2023) では ASI によって構成される確率的近傍の中から，さらに locally informed に次の動きを選ぶことを提案し， 適応的確率近傍 (ARNI: Adaptive Random Neighbourhood Informed) サンプラーと呼んでいる．これにより ASI で上がりきらなかった採択率を押し上げつつ，計算量を抑えつつも良い近傍を提案するメカニズムを取り入れることができる．

これにより \(p\) に依らない収束だけでなく，計算複雑性も \(p\) の次元に対してスケールするものが得られると期待される．

3.9 非可逆なサンプラー

Informed MCMC とは，連続空間上で言えば，MALA などの勾配情報を利用したサンプラーである．このような乱歩 MH 法の修正として得られる効率的なサンプラーを (X. Liang et al., 2022) は 近傍サンプラー (neighbourhood sampler) と呼んでいる．

MALA などの Langevin 拡散を元にした乱歩 MH 法は革新的であったが，現在最も効率的なサンプラーは，局所的な動きを廃した HMC 法と，非可逆な動きを達成する PDMP (Piecewise Deterministic Markov Process) / ECMC (Event-Chain Monte Carlo) である．

離散空間上でもこれらのサンプラーに対応するものは高い効率を示すだろうと思われる．

一般の離散空間上でも局所性の打開には (Nishimura et al., 2020)，可逆性の打開には (Koskela, 2022) などの試みがあるが，殊に変数選択に関しては Sticky PDMP (Bierkens et al., 2023) という画期的な手法が開発されている．

これに関しては次稿で詳しく取り上げる：

4 文献紹介

変数選択のための事前分布とその \(R^2\) 上に定める事前分布については (12.7 節 Gelman et al., 2020) で丁寧に議論されている．

この第一のアプローチ・縮小事前分布については (Bhadra et al., 2019) のレビューがある．他には (Jim E. Griffin and Brown, 2021), (Jim E. Griffin and Brown, 2017), (Hahn and Carvalho, 2015) が詳しい．

(George and McCulloch, 1993) による変数選択法が (Chapter 9 Hoff, 2009) で取り上げられている．

ベイズ変数選択手法の概観は (X. Liang et al., 2023) や (Jim E. Griffin, 2024) のイントロに圧倒されるほどまとまっている．(Jim E. Griffin, 2024) ではモデルの空間上に得られた事後分布の情報を効果的に表示するための「信用区間」の構成法を提案している．

References

Barr, D. J., Levy, R., Scheepers, C., and Tily, H. J. (2013). Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of Memory and Language, 68(3), 255–278.

Bhadra, A., Datta, J., Polson, N. G., and Willard, B. (2019). Lasso Meets Horseshoe: A Survey. Statistical Science, 34(3), 405–427.

Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Brown, P. J., Vannucci, M., and Fearn, T. (1998). Bayesian wavelength selection in multicomponent analysis. Journal of Chemometrics, 12(3), 173–182.

Carvalho, C. M., Polson, N. G., and Scott, J. G. (2009). Handling sparsity via the horseshoe. In D. van Dyk and M. Welling, editors, Proceedings of the twelfth international conference on artificial intelligence and statistics,Vol. 5, pages 73–80. Hilton Clearwater Beach Resort, Clearwater Beach, Florida USA: PMLR.

Carvalho, C. M., Polson, N. G., and Scott, J. G. (2010). The horseshoe estimator for sparse signals. Biometrika, 97(2), 465–480.

Castillo, I., Schmidt-Hieber, J., and Vaart, A. van der. (2015). Bayesian linear regression with sparse priors. The Annals of Statistics, 43(5), 1986–2018.

Gelman, A., Hill, J., and Vehtari, A. (2020). Regression and other stories. Cambridge University Press.

George, E. I., and McCulloch, R. E. (1993). Variable selection via gibbs sampling. Journal of the American Statistical Association, 88(423), 881–889.

George, E. I., and McCulloch, R. E. (1997). APPROACHES FOR BAYESIAN VARIABLE SELECTION. Statistica Sinica, 7(2), 339–373.

Ghosh, J., Li, Y., and Mitra, R. (2018). On the Use of Cauchy Prior Distributions for Bayesian Logistic Regression. Bayesian Analysis, 13(2), 359–383.

Godsill, S. J. (2001). On the relationship between markov chain monte carlo methods for model uncertainty. Journal of Computational and Graphical Statistics, 10(2), 230–248. doi: 10.1198/10618600152627924.

Green, P. J. (1995). Reversible jump markov chain monte carlo computation and bayesian model determination. Biometrika, 82(4), 711–732.

Griffin, Jim E. (2024). Expressing and visualizing model uncertainty in bayesian variable selection using cartesian credible sets.

Griffin, Jim E., and Brown, P. (2017). Hierarchical Shrinkage Priors for Regression Models. Bayesian Analysis, 12(1), 135–159.

Griffin, Jim E., and Brown, P. J. (2021). Bayesian global-local shrinkage methods for regularisation in the high dimension linear model. Chemometrics and Intelligent Laboratory Systems, 210, 104255.

Griffin, J. E., Łatuszyński, K. G., and Steel, M. F. J. (2021). In search of lost mixing time: Adaptive markov chain monte carlo schemes for bayesian variable selection with very large p. Biometrika, 108(1), 53–69.

Hahn, P. R., and Carvalho, C. M. (2015). Decoupling shrinkage and selection in bayesian linear models: A posterior summary perspective. Journal of the American Statistical Association, 110(509), 435–448. doi: 10.1080/01621459.2014.993077.

Hans, C. (2009). Bayesian lasso regression. Biometrika, 96(4), 835–845.

Hans, C. (2011). Elastic net regression modeling with the orthant normal prior. Journal of the American Statistical Association, 106(496), 1383–1393. doi: 10.1198/jasa.2011.tm09241.

Hastie, T., Tibshirani, R., and Wainwright, M. (2015). Statistical learning with sparsity: The lasso and generalizations. Chapman; Hall/CRC.

Hoeting, J. A., Madigan, D., Raftery, A. E., and Volinsky, C. T. (1999). Bayesian model averaging: a tutorial (with comments by M. Clyde, David Draper and E. I. George, and a rejoinder by the authors. Statistical Science, 14(4), 382–417.

Hoff, P. D. (2009). A first course in bayesian statistical methods. Springer New York.

Ishwaran, H., and Rao, J. S. (2005). Spike and slab variable selection: Frequentist and Bayesian strategies. The Annals of Statistics, 33(2), 730–773.

Koskela, J. (2022). Zig-zag sampling for discrete structures and nonreversible phylogenetic MCMC. Journal of Computational and Graphical Statistics, 31(3), 684–694. doi: 10.1080/10618600.2022.2032722.

Ley, E., and Steel, M. F. J. (2009). On the effect of prior assumptions in bayesian model averaging with applications to growth regression. Journal of Applied Econometrics, 24(4), 651–674.

Li, D., Dutta, S., and Roy, V. (2023). Model based screening embedded bayesian variable selection for ultra-high dimensional settings. Journal of Computational and Graphical Statistics, 32(1), 61–73.

Liang, F., Paulo, R., Molina, G., Clyde, M. A., and Berger, J. O. (2008). Mixtures of g priors for bayesian variable selection. Journal of the American Statistical Association, 103(481), 410–423. doi: 10.1198/016214507000001337.

Liang, X., Livingstone, S., and Griffin, J. (2022). Adaptive random neighbourhood informed markov chain monte carlo for high-dimensional bayesian variable selection. Statistics and Computing, 32(5), 84.

Liang, X., Livingstone, S., and Griffin, J. (2023). Adaptive MCMC for bayesian variable selection in generalised linear models and survival models. Entropy, 25(9).

Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.

Nishimura, A., Dunson, D. B., and Lu, J. (2020). Discontinuous hamiltonian monte carlo for discrete parameters and discontinuous likelihoods. Biometrika, 107(2), 365–380.

Park, T., and Casella, G. (2008). The bayesian lasso. Journal of the American Statistical Association, 103(482), 681–686. doi: 10.1198/016214508000000337.

Peskun, P. H. (1973). Optimum monte-carlo sampling using markov chains. Biometrika, 60(3), 607–612.

Piironen, J., Paasiniemi, M., and Vehtari, A. (2020). Projective inference in high-dimensional problems: Prediction and feature selection. Electronic Journal of Statistics, 14(1), 2155–2197.

Piironen, J., and Vehtari, A. (2015). Projection predictive variable selection using stan+r.

Piironen, J., and Vehtari, A. (2017a). On the Hyperprior Choice for the Global Shrinkage Parameter in the Horseshoe Prior. In A. Singh and J. Zhu, editors, Proceedings of the 20th international conference on artificial intelligence and statistics,Vol. 54, pages 905–913. PMLR.

Piironen, J., and Vehtari, A. (2017b). Sparsity information and regularization in the horseshoe and other shrinkage priors. Electronic Journal of Statistics, 11(2), 5018–5051.

Polson, N. G., and Scott, J. G. (2011). 501Shrink globally, act locally: Sparse bayesian regularization and prediction. In Bayesian statistics 9. Oxford University Press.

Polson, N. G., and Scott, J. G. (2012). On the Half-Cauchy Prior for a Global Scale Parameter. Bayesian Analysis, 7(4), 887–902.

Porwal, A., and Raftery, A. E. (2022). Comparing methods for statistical inference with model uncertainty. Proceedings of the National Academy of Sciences, 119(16), e2120737119.

Robbins, H., and Monro, S. (1951). A stochastic approximation method. The Annals of Mathematical Statistics, 22(3), 400–407.

Shang, Z., and Clayton, M. K. (2011). Consistency of bayesian linear model selection with a growing number of parameters. Journal of Statistical Planning and Inference, 141(11), 3463–3474.

Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267–288.

Tierney, L. (1998). A note on metropolis-hastings kernels for general state spaces. The Annals of Applied Probability, 8(1), 1–9.

Vehtari, A., Gelman, A., and Gabry, J. (2017). Practical bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27(5), 1413–1432.

West, M. (1987). On scale mixtures of normal distributions. Biometrika, 74(3), 646–648.

Yang, Y., Wainwright, M. J., and Jordan, M. I. (2016). On the computational complexity of high-dimensional Bayesian variable selection. The Annals of Statistics, 44(6), 2497–2532.

Zanella, G. (2020). Informed proposals for local MCMC in discrete spaces. Journal of the American Statistical Association, 115(530), 852–865.

Zanella, G., and Roberts, G. (2019). Scalable importance tempering and bayesian variable selection. Journal of the Royal Statistical Society Series B: Statistical Methodology, 81(3), 489–517.

Zhou, Q., Yang, J., Vats, D., Roberts, G. O., and Rosenthal, J. S. (2022). Dimension-free mixing for high-dimensional bayesian variable selection. Journal of the Royal Statistical Society Series B: Statistical Methodology, 84(5), 1751–1784.

Footnotes

1. 例えば (Barr et al., 2013) では検証的仮説検定の設定で，どこまでランダム効果をモデルに入れるかを議論しており，「全部入れるべき」という結論を一定の前提の下で導いている．

2. (Hahn and Carvalho, 2015, p. 436) は local scale mixture と呼んでいる．他にこの観点は (Jim E. Griffin and Brown, 2017), (Polson and Scott, 2012) でも議論されている．

3. 変数減少法やステップワイズ法などのヒューリスティックな方法に対しての「確率的探索法」という名称だったのだと思われる．特に (George and McCulloch, 1993) ではデータ拡張に基づく Gibbs サンプラーを用いており，その様子が「確率的探索」に見えるのだと思われる．