ベイズデータ解析６

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

関連記事

回帰モデルや分散分析では，暗黙裡に応答変数が連続であることが仮定されている．

本節では質的な変数，特に順序構造がある離散変数のモデリングを考える．このようなものを 順序応答 (ordinal response) という．

このようなデータには，多くの場合背後に 連続潜在変数 を仮定してモデリングを行う．

その結果，潜在変数の存在が Gibbs サンプラーの構成を容易にする．

1 ２項モデル

1.1 はじめに

\(0,1\) の確率変数の分布は，Bernoulli 分布 \(\mathrm{Ber}(p)=\mathrm{Bin}(1,p)\) によって記述できる．

この際，パラメータ \(p\) を代理の応答変数として回帰分析がなされることになる．

多くの場合，リンク関数 \(g\) に関して，\(g(p)\) を線型の予測子 \(\beta^\top X\) で回帰する．Bernoulli 分布は指数型分布族の例であるため，このようなモデルは 一般化線型モデル の例になる．

1.2 ロジスティックモデル

仮に変数 \(y_i\sim\mathrm{Ber}(p)\) に応じて， \[ X_i|Y_i=i\sim\operatorname{N}(\mu_i,\sigma^2),\qquad i\in\{0,1\} \] として説明変数 \(X_i\) が決まっていたとする．

このような状況で，\(X_i\) はある \(\alpha,\beta\) に関して次のロジットモデルを満たす：¹ \[ \operatorname{logit}(p_i)=\alpha+\beta x_i. \]

1.3 潜在変数解釈

\(P(\mu,\sigma^2)\) を正規分布やロジスティック分布などの対称な分布，\(F\) を \(P(0,1)\) の分布関数とする．このとき，プロビットまたはロジスティックモデル \[ \operatorname{P}[Y_i=1|X_i]=F(X_i^\top\beta) \] は，潜在変数 \(Y_i^*\) が存在して \[ Y_i=1_{\mathbb{R}_+}(Y_i^*),\qquad Y_i^*\sim P(X_i^\top\beta,1) \tag{1}\] として結果が決まっているものとも解釈できる．これは \[ \operatorname{P}[Y_i=1|X_i]=\operatorname{P}[Y_i^*>0|X_i]=\operatorname{P}[-U\le X_i^\top\beta],\qquad U\sim P(0,1), \] が成り立つためである．

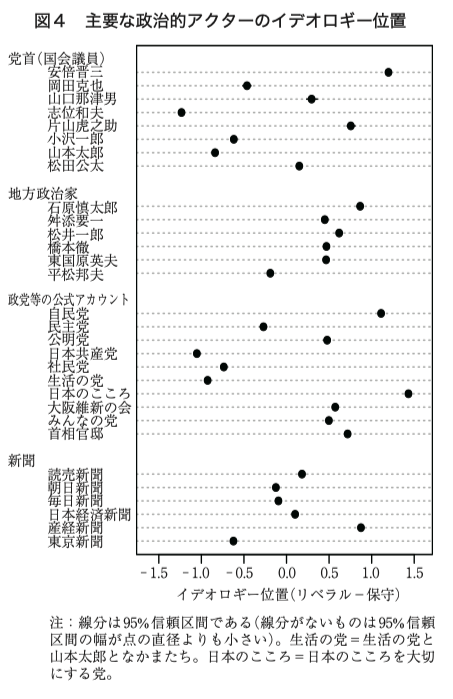
この潜在変数 \(Y_i^*\) は単位 \(i\in[N]\) の潜在的な尺度として解釈できる．これを用いて因子分析様の解析を行う例には 理想点推定 もある．

一方で \(Y_i^*\) の存在は Gibbs サンプラーの構成を容易にする (Albert and Chib, 1993)．

\(F\) を \(t\)-分布とした場合，これを robit モデル (Liu, 2004) という (15.6 節 Gelman et al., 2020)．\(t\) 分布の自由度を無限大にした場合が probit モデルに相当する．

第 2.3 節でまた別の，効用関数による潜在変数表現を扱う．

1.4 順序応答

前節 1.3 の潜在変数解釈は容易に２値応答以外の場合に拡張できる．その結果多項モデルを用いたソフトマックス回帰 2.2 などとは別のアプローチが，多値順序応答に対して可能になる．

\(y\in n+1:=\{0,1,\cdots,n\}\) という順序を持った順序応答の場合でも \[ \chi(u)=1_{(c_0,\infty)}(u)+1_{(c_1,\infty)}(u)+\cdots+1_{(c_n,\infty)}(u) \] という階段関数を用いて \[ Y_i=\chi(Y_i^*),\qquad Y_i^*\sim P(X_i^\top\beta,1) \] というデータ生成過程を想定できる．

これはそのまま 順序多項回帰 (ordered multinomial regression) (Walker and Duncan, 1967) に相当する．

この場合 \(c_0=0\) とし，それに応じて \(Y_i^*\sim P(X_i^\top\beta-c_0,1)\) とする径数付けを採用する場合も多い．

ベイズ推論は \(\chi\) を特徴付ける点 \((c_0,c_1,\cdots,c_n)\) 上に事前分布を置くことで実行できるが，順位尤度 (rank likelihood) を通じた議論により，\(g\) を特定せずとも Gibbs サンプラーによる推論が可能である (Section 12.1.2 Hoff, 2009)．

1.5 識別可能性と分離

線型回帰において，共線型性 があると識別可能性が失われる．ロジスティック回帰にはもう一つ識別不可能性の典型的な原因がある．

多くの点推定手法において，説明変数の線型変換が極めて強力な説明変数になる場合，やはり「正解」が何個も存在する状況が現れるため，モデルの非識別性が暗黙のうちに問題になる．これを 分離 (separation) という (Gelman et al., 2014, p. 412)．

特に最尤推定法，一様事前分布を持ったベイズ推定は不安定になるが，このような場合でも裾の重い事前分布を採用することでベイズ推論が安定的に実行可能である（同様にして正則化を加えた最尤推定も可能である） (Gelman and Hill, 2006, p. 104)．

特に係数に（互いに独立な） \(t\)-分布 \(t(\nu,0,s)\) を仮定する，ロバスト性を意識した設定がデフォルトと理解されている (Gelman et al., 2014, p. 412)．

ただし，\(\nu,s\) は説明変数のスケールに合わせてなるべく無情報になるように設定される．\(s\to\infty\) の極限が一様分布になり，分離の問題にセンシティブになっていく．

\(g(\mu)=:\theta\) のそれぞれの値に関して，成功試行と失敗試行が同数現れる尤度は \(\frac{e^{\theta/2}}{1+e^\theta}\) となり，これは \(t(7,0,2.5)\) でよく近似される．

\(t(1,0,2.5)\) から \(t(7,0,2.5)\) はいずれも \([-5,5]\) に多くの重みを持つが，\(\nu=1\) に近いほど裾が重くなる．\(g(\mu)\) のスケールで \(+5\) をすることは，確率を \(0.01\) から \(0.5\) にすることに等しいため，切片項への \(t\)-事前分布は \(\mu\in[0.01,0.99]\) を強く仮定していることは含意する．

1.6 ベイズ計算

一般に二項回帰モデルはベイズ計算法の良いベンチマークになる．

大規模なモデルでは事前調整ありの期待伝搬と乱歩 MH が強いが，Gibbs サンプラーや SMC サンプラーも十分良い性能を示す一方で，NUTS などの HMC ベースの手法は苦しむという (Chopin and Ridgway, 2017)．

特に説明変数の次元 \(p\) が大きい場合の事後分布サンプリングはまだまだ難しいことが知られている．

1.7 分散分析

(Gelman et al., 2014, p. 423) 16.5 節は良い例である．アメリカ合衆国における国民の投票行動をロジットリンクにより二項モデルで一般化線型回帰をしている．Bayes ANOVA により人種による大きな効果と同時に，人種と州の強い交差効果が発見できている．

1.8 選択モデル

計量経済学の分野で古くから使われている潜在変数表現 1.3 の拡張として，選択モデル (choice model) がある．

これに関しては 階層ロジスティックモデルの稿 で詳しく扱う．

2 多項モデル

2.1 はじめに

順序応答 \(y\in\{1,\cdots,k\}\) の場合，\(y\) がカウントを表す場合は Poisson モデル，複数回繰り返される独立試行の成功回数である場合は二項モデルが考えられる．

一方で多項モデル（正確にはカテゴリカルモデル） \[ Y\sim\operatorname{Cat}(\alpha_1,\cdots,\alpha_k),\qquad\sum_{j=1}^k\alpha_j=1, \] も想定できる．\(y\) が全く構造を持たない名目 (nominal) 応答である場合，ほぼ唯一の選択である．

2.2 名目応答に対する多項モデル

名目応答が \(k\) 次元ベクトル \(y_i\in\mathbb{N}^k\) の形で与えられている場合， \[ y_i\sim\mathrm{Mult}(n_i;\alpha_{i1},\cdots,\alpha_{ik}),\qquad\sum_{j=1}^k\alpha_{ij}=1, \] というモデルを想定できる．\(n_i\equiv1\) の場合，応答を one-hot 表現にしたカテゴリカルモデルに対応する．

リンク関数 \(g\) は，特定のカテゴリ \(j=1\) を 基準 (reference) として \(g(\alpha):=\log\frac{\alpha}{\alpha_{i1}}\) と定めることが多い： \[ \log\frac{\alpha_{ij}}{\alpha_{i1}}=X_i\beta^{(j)}. \] これを 多項ロジスティック回帰 (multinomial logistic regression) (Ding, 2024, p. 228) または ソフトマックス回帰 (softmax regression) (Kruschke, 2015, p. 650) という： \[ \alpha_{ij}=\operatorname{softmax}(X_i\beta^{(j)})=\frac{e^{X_i\beta^{(j)}}}{\sum_{l=1}^ke^{X_i\beta^{(l)}}},\qquad \beta^{(1)}=0. \]

係数は，説明変数が \(1\) 単位増加した際の，参照カテゴリ \(j=1\) に対する対数オッズ比の変化を表す．

一方で条件付きロジスティック回帰 (conditional logistic regression) なる方法もある (22.2節 Kruschke, 2015, pp. 655–)．

2.3 効用による表現

多項ロジスティックモデルも潜在変数解釈 1.3 が可能である．

\(k\) 次元の標準 Gumbel 分布に従う誤差 \(\epsilon_{i-}\in\mathbb{R}^k\) に関して， \[ U_{il}:=\beta_l^\top X_l+\epsilon_{il},\qquad l\in[k], \] を潜在的な効用とし， \[ Y_i:=\operatorname*{argmax}_{l\in[k]}U_{il} \] によって応答が定まると見ることができる (McFadden, 1974)．

ただしこの表示からはっきりわかるように，各選択肢を選ぶ効用は他の選択肢とは独立に決まることが仮定されている．これを IIA (Independence of Irrelevant Alternatives) ともいう．

このような仮定は，文脈効果（「選択肢セットの配置によって消費者の選好する選択肢が容易に変化する」 (竹内真登 and 猪狩良介, 2022) 現象）を主な関心とするマーケティングの分野では非常に不適当なものになる．

2.4 順序応答に対する多項モデル

応答 \(y_i\in\{1,\cdots,k\}\) に自然な順序がある場合，カテゴリ確率 \(\alpha_{i1},\cdots,\alpha_{ik}\) の代わりに累積確率 \[ \pi_{ij}:=\sum_{l\le j}\alpha_{il}=\operatorname{P}[Y_i\le j] \] を考え，モデルにその順序構造を自然に伝えることができる．

この場合リンク関数はロジットやプロビットが使える： \[ \log\frac{\pi_{ij}}{1-\pi_{ij}}=X_i\beta^{(j)}. \] \(\beta^{(j)}\equiv\beta\) と取ることも多い．

このモデルを，\(g\) がロジットである場合順序ロジスティック回帰 (ordinal / ordered logistic regression) (McCullagh, 1980) といい (Kruschke, 2015, p. 671)，\(g\) がプロビットである場合順序プロビット回帰 (ordered probit regression) という．

異なるパラメータ付け \[ \operatorname{logit}(\pi_{ij})=\beta_0^{(j)}-X_i\beta \] を用いた場合，これを 比例オッズロジットモデル (proportional odds logit model) ともいう (Ding, 2024, p. 232)．

2.5 Poisson モデル

応答が \(\{1,\cdots,k\}\) カテゴリのカウント \(y=(y_1,\cdots,y_k)\) である場合， \[ y_i\overset{\text{i.i.d.}}{\sim}\mathrm{Pois}(\lambda_i) \] というモデルを想定できる．

カウント総数 \(n:=\sum_{i=1}^ky_i\) が既知である場合，これに関して条件付けると \[ y\bigg|\sum_{i=1}^ky_i=n\sim\mathrm{Mult}(n;\alpha_1,\cdots,\alpha_k),\qquad\alpha_i:=\frac{\lambda_i}{\sum_{j=1}^k\lambda_j} \] という周辺モデルを想定したことになる．

リンク関数には対数関数 \(g=\log\) を用いることが多い．

2.6 トーナメントデータ

一度に２人の単位が勝負をし，どちらが勝利したかのデータに対する標準的なモデルに，(Bradley and Terry, 1952) モデルがある．国際チェス連盟や欧州囲碁連盟で選手のランクづけにも採用されている (Hastie and Tibshirani, 1998)．

このモデルでは各プレイヤーに能力パラメータ \(\alpha_i\) を与え，能力の差のロジスティック関数 \[ \operatorname{P}[i\;\text{defeats}\;j]=\frac{e^{\alpha_i-\alpha_j}}{1+e^{\alpha_i-\alpha_j}} \] という確率で勝敗が決まるとする．\(\lambda_i:=e^{\alpha_i}\) というパラメータづけもよく用いられる．

このモデルは「勝利」「引き分け」「敗北」の３応答に対する確率モデルを調節することで，引き分け (Rao and Kupper, 1967) や先手有利 (Davidson and Beaver, 1977), (Agresti, 2012) などの情報も取り入れられるように簡単に拡張できる．

このように２値応答ではなく多値応答とみても，前節の Poisson モデルの定式化に帰着させることで，一般化線型モデリングの枠組みに合流させることができる (Gelman et al., 2014, pp. 427–428)．

2.7 順位データ

ランキングデータは，トーナメントのような常に１対１比較のみを通じて情報が得られるわけではない．多者比較 (multiple comparison) も取り入れた Bradley-Terry モデルより一般的なものが (Plackett, 1975)-(Luce, 1959) モデルである．

Plackett-Luce モデルでは，参加者 \([K]:=\left\{1,\cdots,K\right\}\) の強さに当たる潜在変数 \(\lambda_k>0\) を導入し，これに比例した「優勝」確率を持つとする．そして順位の決定は，参加者のプールから「勝ち抜け」の１人を決定する独立試行の繰り返しと見て， \[ \operatorname{P}[Y=y|\lambda]=\prod_{j=1}^{K-1}\frac{\lambda_{y_j}}{\sum_{l=j}^K\lambda_{y_l}} \] としてモデリングする．

このモデルは，「陽の目を見る瞬間」 \[ W_k\overset{\text{i.i.d.}}{\sim}\operatorname{Exp}(\lambda_k) \] という到着時刻があり，この時刻の早さで順位が決まる \[ \operatorname{P}[W_{y_1}<\cdots<W_{y_K}|\lambda]=\operatorname{P}[Y=y|\lambda]=\prod_{j=1}^{K-1}\frac{\lambda_{y_j}}{\sum_{l=j}^K\lambda_{y_l}} \] という潜在変数表現を持つ．これは Thurstone 表現 (Thurstone, 1927)，またはランダム効用モデルと呼ばれる (Chapter 9 Diaconis, 1988, p. 167)．

このような潜在変数表現を元にした MM アルゴリズム (Hunter, 2004) や Gibbs サンプラー (Caron and Doucet, 2012) に基づく推論法が存在する．PlackettLuce パッケージ (Turner et al., 2020) も参照．

さらに Plackett-Luce モデルで引き分けを許すように拡張したものが Gibbs サンプラーとともに (Henderson, 2024) で提案されている．順位データとレーティング（点数付け）のデータを同時に扱うことができるような拡張が (Pearce and Erosheva, 2025) で提案されている．

2.8 対数線型モデル

\(y\) も \(x\) も名目応答である場合，これは分割表解析の問題になる．

この際には 対数線型モデル (log-linear model) も考えられる．

それぞれのセルに Poisson モデルをおき，そのパラメータを代理応答変数として，対数リンクにより一般化線型回帰を行うものである．

このモデルは，サンプルサイズ \(N\) が既知の場合などの下では，周辺分布に多項モデルをおくことに等価である (Yates, 1934)．

対数線型モデルは分割表解析だけでなく，多重代入法 などの欠測データ解析にも応用される．

3 コピュラモデル

3.1 はじめに

以上の質的変数のモデルは，いずれも潜在的な連続変数の離散化としてデータを理解するものであった．

仮にこの潜在変数により興味がある場合，この潜在変数をより具体的に，特にその相関構造をモデリングしたいということになる．

(Lopez-Paz et al., 2013)

4 文献紹介

(Gelman et al., 2014) の 16 章で一般化線型モデルが扱われている．(Kruschke, 2015) はさらに詳しく，22 章で名目応答，23 章で順序応答，24 章でカウントデータを扱っている．

(12 章 Hoff, 2009) にて正規コピュラモデルが ordinal probit モデルの，潜在変数を多次元に拡張した場合として導入されている．

(Chib and Winkelmann, 2001) はリンクを対数関数とし，Poisson 周辺分布を持つカウントデータのコピュラモデリングを実行している．

(Quinn, 2017) は連続確率変数に対してコピュラモデリングを実行している．

References

Agresti, A. (2012). Categorical data analysis. John Wiley & Sons, Inc.

Albert, J. H., and Chib, S. (1993). Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association, 88(422), 669–679.

Bradley, R. A., and Terry, M. E. (1952). Rank analysis of incomplete block designs: I. The method of paired comparisons. Biometrika, 39(3/4), 324–345.

Caron, F., and Doucet, A. (2012). Efficient bayesian inference for generalized bradley–terry models. Journal of Computational and Graphical Statistics, 21(1), 174–196.

Chib, S., and Winkelmann, R. (2001). Markov chain monte carlo analysis of correlated count data. Journal of Business & Economic Statistics, 19(4), 428–435.

Chopin, N., and Ridgway, J. (2017). Leave Pima Indians Alone: Binary Regression as a Benchmark for Bayesian Computation. Statistical Science, 32(1), 64–87.

Davidson, R. R., and Beaver, R. J. (1977). On extending the bradley-terry model to incorporate within-pair order effects. Biometrics, 33(4), 693–702.

Diaconis, P. (1988). Group representations in probability and statistics,Vol. 11. Institute of Mathematical Statistics.

Ding, P. (2024). Linear model and extensions.

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014). Bayesian data analysis. Boca Raton : CRC Press.

Gelman, A., and Hill, J. (2006). Data analysis using regression and multilevel/hierarchical models. Cambridge University Press.

Gelman, A., Hill, J., and Vehtari, A. (2020). Regression and other stories. Cambridge University Press.

Hastie, T., and Tibshirani, R. (1998). Classification by pairwise coupling. The Annals of Statistics, 26(2), 451–471.

Henderson, D. A. (2024). Modelling and Analysis of Rank Ordered Data with Ties via a Generalized Plackett-Luce Model. Bayesian Analysis, 1–29.

Hoff, P. D. (2009). A first course in bayesian statistical methods. Springer New York.

Hunter, D. R. (2004). MM algorithms for generalized Bradley-Terry models. The Annals of Statistics, 32(1), 384–406.

Kruschke, J. K. (2015). Doing bayesian data analysis: A tutorial with r, JAGS, and stan. London ; Tokyo : Academic Press.

Liu, C. (2004). Robit regression: A simple robust alternative to logistic and probit regression. In Applied bayesian modeling and causal inference from incomplete‐data perspectives, pages 227–238. John Wiley & Sons, Ltd.

Lopez-Paz, D., Hernández-Lobato, J. M., and Zoubin, G. (2013). Gaussian process vine copulas for multivariate dependence. In S. Dasgupta and D. McAllester, editors, Proceedings of the 30th international conference on machine learning,Vol. 28, pages 10–18. Atlanta, Georgia, USA: PMLR.

Luce, R. D. (1959). Individual choice behavior. John Wiley.

McCullagh, P. (1980). Regression models for ordinal data. Journal of the Royal Statistical Society: Series B (Methodological), 42(2), 109–127.

McFadden, D. (1974). Frontiers in econometrics. In P. Zarembka, editor, pages 105–142. Academic Press.

Pearce, M., and Erosheva, E. A. (2025). Modeling preferences: A bayesian mixture of finite mixtures for rankings and ratings. Journal of the American Statistical Association, 0(0), 1–12.

Plackett, R. L. (1975). The analysis of permutations. Journal of the Royal Statistical Society. Series C (Applied Statistics), 24(2), 193–202.

Quinn, K. M. (2017). Bayesian factor analysis for mixed ordinal and continuous responses. Political Analysis, 12(4), 338–353.

Rao, P. V., and Kupper, L. L. (1967). Ties in paired-comparison experiments: A generalization of the bradley-terry model. Journal of the American Statistical Association, 62(317), 194–204.

Thurstone, L. L. (1927). A law of comparative judgement. Psychological Review, 34(4), 273–286.

Turner, H. L., Etten, J. van, Firth, D., and Kosmidis, I. (2020). Modelling rankings in r: The PlackettLuce package. Computational Statistics, 35(3), 1027–1057.

Walker, S. H., and Duncan, D. B. (1967). Estimation of the probability of an event as a function of several independent variables. Biometrika, 54(1-2), 167–179.

Yates, F. (1934). Contingency tables involving small numbers and the χ2 test. Supplement to the Journal of the Royal Statistical Society, 1(2), 217–235.

竹内真登, and 猪狩良介. (2022). 文脈効果を考慮したコンジョイント分析による購買予測. 流通研究, 24(2), 17–32.

Footnotes

1. (Ding, 2024, p. 222) も参照．