理想点解析・多次元展開法・項目応答理論

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1 政治学における理想点解析

1.1 はじめに

理想点推定 は (Poole and Rosenthal, 1991) 以来，政治学において各アクターのイデオロギーを定量化・可視化する方法論として用いられている．

理想点推定は，政治学における 空間モデリング の重要な一環であり，現代ではイデオロギーの「近さ」を定量化する際の多次元展開法の一種として，理想点推定を位置付けることができる．

理想点推定の展開

理想点推定は 態度測定 (飽戸弘, 1966) や 議員尺度化 (legislative scaling) (Jackman, 2001)，または 空間分析 (spatial analysis) (Davis et al., 1970), (岡田謙介 and 加藤淳子, 2016) とも呼ばれる．

政治過程とは合意形成の過程である．これを各アクターが政策空間上に選好分布を持つとしてモデリングし，その上でのアクターの行動を分析することで政治・立法・司法過程の理解を試みることを 空間モデリング (Davis et al., 1970), (Enelow and Hinich, 1984) という．

空間モデリングの政治学的な理論的根拠として 空間（競争）理論 (Downs, 1957) が源流にある．

政治学における空間理論とは，イデオロギーの「近さ」が影響力を持つとする枠組みであり，はじめは１次元空間上での選挙と投票行動の公理的な分析に用いられた．

1.2 空間競争理論 (Downs, 1957)

空間理論はもともと，ゲーム理論における交渉理論 (bargaining theory) において (Hotelling, 1929) が雑貨店の立地の情報を考慮に入れたことから始まった．

政治学，特に選挙競争において (Black, 1948) が空間競争理論，特に一次元の政策空間を導入し，公理的な議論を行なった：

(中位投票者定理 Black, 1948)¹

一次元の政策空間上に投票者が単峰性の選好分布を持つ際，中位政策が Condorcet 勝者となる．

(Downs, 1957) は (Black, 1948) が用意した政策空間とゲーム理論を合流させ，選挙競争と投票行動の分析に応用した．

(Downs, 1957; Hotelling, 1929)²

１次元の政策空間上の２政党競争において，いくつかの仮定の下で，ナッシュ均衡は両政党が中位政策を採用することである．

1.3 空間競争モデルと理想点

(Hotelling, 1929)-(Downs, 1957) のアプローチは政治的競争のモデルの出発点となり，政治的競争を人工的な空間上でモデリングする手法が広がった．

例えば多くの選挙結果を分析する際，政策空間内での中位政策の位置の特定や，実際の政党の政策の中位政策からのズレが重要な意味を持つようになった．

例：赤い州と青い州の問題

米国での投票行動において，個人レベルでの選考と州レベルでの選考とが食い違うという問題が 21 世紀以来有名になっている (Gelman, 2014)．

端的に言えば，政策的にはリベラルに位置する民主党は貧困層の見方であるが，その主な得票源は富裕層の多い州からのものである．

これは中位投票者が中産階級に位置するためであるという見方が一つ説明のつく仮説である (浅古泰史, 2016, p. 78)．

一方で，ベイズ階層モデリングによる解析によって，各州の投票行動が大きく違うことが判明し，New York や California のように裕福な州では収入が投票行動に全く影響しないこともわかっている (Gelman, 2014)．

このように政策空間上にアクターをマッピングし，その上で競争をモデリングする手法は 空間モデル (spatial model) とも呼ばれる．

特にアクターが政策空間上に持つ選好分布の最頻値を 理想点 (ideal point) という．

さらには多次元に拡張された理論が多くの経済分析に応用されており，価格などの一次元的な尺度に限らずより一般的な選好を考慮した交渉の議論が可能になっている．³

one way to try to account for political choices is to imagine that each chooser occupies a fixed position in a space of one or more dimensions, and to suppose that every choice presented to him is a choice between two or more points in that space. (MacRae, 1958)

1.4 理想点解析の発展

現代では空間理論と空間モデルは，投票などの政治過程，そして議会などにおける立法過程の研究に応用される．広く交渉における空間理論については (林光, 2016) も参照．

さらには純粋にイデオロギーという概念を定量化することにも用いられる．

古くイデオロギーとは一見バラバラに見える政治的問題の相互の繋がりに関する信念体系である (Converse, 2006)．

特にリベラル - 中道 - 保守，左 - 右などといった空間的な理解は長らく用いられているものであるが，これは本人が既存のイデオロギーに倣って行動しているというより，よく見られる一貫した行動パターンに名前をつけたものというべきである (Hinich and Pollard, 1981)．

一貫した行動パターンの分類，その分類がどれほど行動の予測に有用であるか，これらの尺度は統計学の本領というべきである．

1.5 点呼投票データ

理想点解析で最もよく使われるデータとして，各政治家が審議期間にて表明した投票記録，特に 点呼投票 (Roll Call Voting) 記録が用いられる．

点呼投票データを扱う展開法 (roll-call scaling method) として初めに提案されたものが NOMINATE (nominal, three-step estimation) (Poole and Rosenthal, 1985) であり，次の３段階からなる：

1. 議員の理想点の推定
2. 法案に対する応答が対応する点の推定
3. 議員の効用関数のパラメータ推定

NOMINATE の発展

• D-NOMINATE (Poole and Rosenthal, 1991)

  点呼投票データの時系列構造も取り込めるようにした拡張．D は dynamic の略である．

• W-NOMINATE (Poole and Rosenthal, 1997)．

  W は weighted の略であり，パソコン上でも動くように設計されたアルゴリズム．現在は R パッケージ wnominate (Poole et al., 2011) で利用可能．

  (Heckman and Snyder, 1997) は同様の手法を因子分析の言葉で定式化している．

• DW-NOMINATE (McCarty et al., 1997)

1.6 BIRT (Clinton et al., 2004)

NOMINATE の方法には政策次元が \(K=1\) などの隠匿された仮定があり，これらの仮定を緩めることが必ずしも簡単ではなく，モデル比較の議論となるとほとんど十分な理論的根拠を持たなかった．

理想点推定を統計モデル，特に項目反応モデル（第 3 節）とみなし，従来は局外母数とみなされた項目毎の母数も，ベイズの枠組みで同時に推論・モデル比較を行うことが (Jackman, 2000), (Jackman, 2001), (Clinton et al., 2004) によって提案された．⁴

\(i\in[N]\) 番目の議員が \(j\in[J]\) 番目の法案に対して賛成 \(y_{ij}=1\) ならば \(\zeta_j\in\mathbb{R}^K\)，反対 \(y_{ij}=0\) ならば \(\psi_j\in\mathbb{R}^K\) として政策空間 \(\mathbb{R}^K\) 上に表現されるとする．

このとき \(i\in[N]\) 番目の議員の理想点 \(x_i\in\mathbb{R}^K\) は， \[\begin{align*} y_{ij}&=1_{\mathbb{R}^+}(y^*_{ij})\\ y^*_{ij}&=\alpha_j+x_i^\top\beta_j+\epsilon_{ij},\qquad\epsilon_{ij}\overset{\text{iid}}{\sim}\mathrm{N}(0,1)\\ &=:\widetilde{x}_i^\top\widetilde{\beta}_j+\epsilon_{ij} \end{align*}\] で定まるとする．

すると次のプロビットモデルが想定されたことになる： \[ \operatorname{P}[y_{ij}=1]=\Phi(\widetilde{x}_i^\top\widetilde{\beta}_j). \]

このモデルは項目反応モデルの文脈で Gibbs サンプリングによる推定が古くから議論されていた (Albert, 1992)．

注：ランダム効用理論との離別

ここでは (Clinton et al., 2004) を踏襲した (Imai et al., 2016) の定式化に従った．

(Clinton et al., 2004) の定式化は ランダム効用理論 (random utility framework) (McFadden, 1976) に従い，議員 \(i\in[N]\) の効用関数を用いていたという点で NOMINATE (Poole and Rosenthal, 1985) を踏襲していた．

だが，(Jackman, 2001) ではこれを統計モデル（項目反応モデル）として解釈する際に \(U_i\) を排している．

(Clinton et al., 2004) の設定では，理想点 \(x_i\in\mathbb{R}^K\) は次の効用関数 \(U_i:\{\zeta_j,\psi_j\}_{j=1}^J\to\mathbb{R}\) を通じて意思決定に影響するとした： \[ U_i(\zeta_j)=-\lvert x_i-\zeta_j\rvert^2+\eta_{ij}, \] \[ U_i(\psi_j)=-\lvert x_i-\psi_j\rvert^2+\nu_{ij}. \] ただし，\(\eta_{ij},\nu_{ij}\) は互いに独立な Gauss 誤差とし，\(\eta_{ij}-\nu_{ij}\overset{\text{iid}}{\sim}\mathrm{N}(0,\sigma_j^2)\) とする．

最終的に議員 \(i\in[N]\) は \[ y_{ij}=1_{\left\{U_i(\zeta_j)>U_i(\psi_j)\right\}} \] として投票行動を表現する．

この統計モデルは \[ \operatorname{P}[y_{ij}=1]=\Phi(\beta_j^\top x_i-\alpha_j) \] \[ \beta_j:=\frac{2(\zeta_j-\psi_j)}{\sigma_j},\qquad\alpha_j=\frac{\zeta_j^\top\zeta_j-\psi_j^\top\psi_j}{\sigma_j} \] という probit モデルに等価になる．⁵

なお誤差 \(\eta_{ij},\nu_{ij}\) を極値分布に従うとすると logit モデルを得る．logit モデルは NOMINATE (Poole and Rosenthal, 1985) 発表前に計算資源が少なかった時代に用いられていたが，その後は誤差の正規性の仮定が優先された (Poole and Rosenthal, 2001)．

効用関数 \(U\) は NOMINATE では Gauss 密度，(Heckman and Snyder, 1997) と (Clinton et al., 2004) では二次関数を用いていた．

(Clinton et al., 2004) では \(x_i,\widetilde{\beta}_j\) に独立な共役事前分布 \[ p(x_1,\cdots,x_N)=\prod_{i=1}^N\phi_K(x_i;\mu_x,\Sigma_x) \] \[ p(\widetilde{\beta}_1,\cdots,\widetilde{\beta}_J)=\prod_{j=1}^J\phi_{K+1}(\widetilde{\beta}_j;\mu_{\widetilde{\beta}},\Sigma_{\widetilde{\beta}}) \] を仮定した．

(Clinton et al., 2004) ではこのモデルの２パラメータの項目反応モデルとの対応に基づいて，データ拡大に基づく Gibbs サンプラーによる推定が WinBUGS (Lunn et al., 2000) によりなされ，R パッケージに実装され，現在も pscl (Political Science Computational Laboratory) パッケージ (Zeileis et al., 2008) に実装されている．

単一指標モデルとの関係

被説明変数が \(y_{ij}\in\{0,1\}=2\) であるこのモデルは，計量経済学では 二項選択モデル (binary choice model) として知られている (Chapter 25 Hansen, 2022, p. 801)．

計量経済学ではプロビット，ロジットモデルの他に，リンク関数 \(G\) の関数系を局外母数としたセミパラメトリックモデルである 単一指標モデル (single-index model) \[ \operatorname{P}[y_{ij}=1]=G(x^\top_i\beta_j)+\epsilon_{ij} \] が考えられる．

特に \[ y_{ij}=1_{\mathbb{R}^+}\biggr(\widetilde{x}_i^\top\widetilde{\beta}_j+\epsilon_{ij}\biggl) \] という（潜在変数）モデルでは，\(\epsilon_{ij}\) の分布関数を \(F\) とすると， \[ Y_{ij}\sim\mathrm{Ber}(F(X^\top_i\beta_j)) \] \[ \operatorname{P}[y_{ij}=1]=F(x^\top_i\beta_j) \] というモデルと等価になり，単一指標モデルに一致する (Section 25.4 Hansen, 2022, p. 804)．

この設定で \(F\) を未知のままでも \(\beta_j\) に関してセミパラメトリック推定ができる (Klein and Spady, 1993)．

ただし，理想点推定の場合のように \(X\) に定数項があると識別可能性が失われるため，追加の制約が必要である．また \(\beta\) も定数倍を除いて識別される．

1.7 ベイズ計算の問題

理想点推定にベイズモデルを立てて MCMC により推定する方法は動的なモデル (Clinton and Meirowitz, 2001), (Martin and Quinn, 2002)，戦略的投票 (Clinton and Meirowitz, 2017), 階層モデリング (Bafumi et al., 2005) へ拡張され，主流の方法となった．

しかし (Martin and Quinn, 2002) では 47 年の米国最高裁データの分析に５日間かかっている．特に pscl (Zeileis et al., 2008) による Gibbs サンプリングがデータの不均衡性によって収束に苦しんでいる可能性がある．

そこでベイズの方法で理想点解析をやりたいが，理想点推定はモデルが大規模になるために効率的な計算手法が必要となっている．

1.8 変分 EM アルゴリズム

(Imai et al., 2016) は高速なベイズ推論のために変分 EM アルゴリズムを提案し，emIRT パッケージに実装している．

種々のタイプのモデル（多値反応モデル，動的モデル，階層モデル，テキストデータ）を考察しているので，種々の理想点解析モデルのレビューとしても有用である．

その共通するアプローチは \(Y^*\) を欠測データと扱い，\(\widetilde{x}_i,\widetilde{\beta}_j\) を同時に EM アルゴリズムにより推定し，特定の基準に基づいてアルゴリズムを停止することである．その途中で変分近似を用いる．

ベイズ的な不確実性の可視化を得るために NOMINATE のようにパラメトリックブートストラップ (Carroll et al., 2009), (Lewis and Poole, 2004) を行う．

(Imai et al., 2016) の変分 EM アルゴリズムにより \(d=1\) 次元空間上の理想点を推定した結果が (三輪洋文, 2017) で公開されている：

Twitter データとプロビットモデルによる理想点推定 (三輪洋文, 2017, p. 51)

1.9 その他のデータ源の探索

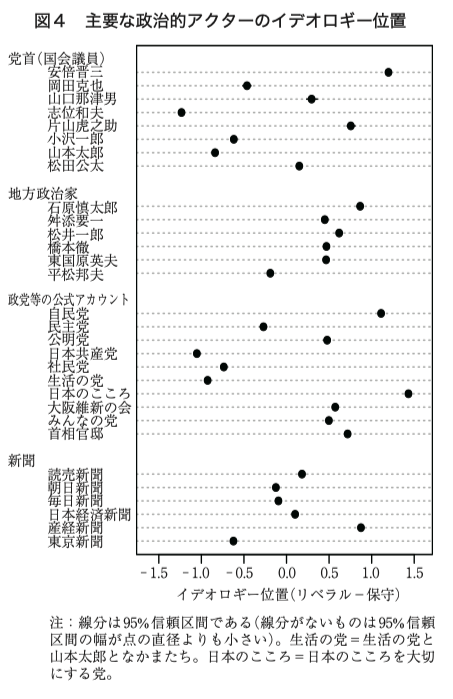
点呼投票データには，政党規律や 票取引 (logrolling) などの戦略的投票行動がある際には，必ずしも個人の政治的信条を反映しないという欠点がある．

そこで点呼投票データの他に有用なデータ源の探索とそれを用いた理想点推定の方法が模索されており，データ統合が最終的な目標として目指されている．

特に日本では政党規律が強く，点呼投票データが適さないため，政治家へのサーベイや質問，専門家調査 (加藤淳子, 2021) によってデータが収集されることが多いという (三輪洋文, 2017), (Miwa and Taniguchi, 2017)．

このテキストベースのアプローチは，政党が公開しているマニフェストなどの客観的なデータも取り入れることが可能であるという点に美点がある (岡田謙介 and 加藤淳子, 2016)．

また近年では，Twitter が政治家の政策と信条の空間的位置について多くの情報を含んでいる情報源として注目されている (Barberá, 2015), (三輪洋文, 2017)．

2 多次元展開法としての理想点解析

2.1 Twitter データと項目反応モデルを通じた多次元尺度展開

(Barberá, 2015) は特に Twitter において誰が誰をフォローしているかのデータに注目した．

\((y_{ij})\in M_n(2)\) を，ユーザー \(i\) がユーザー \(j\) をフォローしているかを２値で表した \(0,1\) 成分行列とし，この関係が政策空間 \(\mathbb{R}^d\) におけるユーザー \(i,j\) の距離の近さによって決定されているとする．

\(\theta_i:[n]\to\mathbb{R}^d\) をユーザーの政策空間への埋め込みとすると，\(g\) をリンク関数として \[ g\biggr(\operatorname{P}[Y_{ij}=1\,|\,\alpha_j,\beta_i,\theta]\biggl)=\alpha_i+\beta_j-d(\theta_i,\theta_j) \] とするのである．

ただし，\(\alpha_j\) は知名度，\(\beta_i\) は政治的関心を表す説明変数とした．

これにより Gibbs サンプラーにより \(\alpha,\beta,\theta\) の推定が可能になるが，この方法では推定が遅く，また大規模なデータや偏りのあるデータに弱い．

この問題点は Zig-Zag サンプラーによって解決され，さらに推定が高速になる．詳しくは次の稿も参照：

2.2 多次元展開法としての展開

(Bakker and Poole, 2013) は理想点解析を多次元尺度法と見て，ベイズ化の方法を提案している．

多次元空間への多次元尺度構成法は，非線型次元縮約法，多様体学習法，埋め込み法などといった種々の名前の下で考察されている．

逆に言えば，これらの他手法と比較したり，長所と短所を洗い出すことで，個々の手法に対する理解が深まるかもしれない．

(Escolar et al., 2023) では特許のデータを用い，各企業を技術空間 \(\mathbb{R}^{430}\) 内に埋め込んだ後，mapper (Singh et al., 2007) によりグラフ化したところ，企業の独自戦略が可視化されたという．

3 項目反応理論

3.1 はじめに

(Jackman, 2001), (Clinton et al., 2004) でも自覚されているように，理想点解析は多次元尺度構成法であると同時に，点呼投票という２値応答に特化した項目反応理論とも見れる．

項目反応理論 (IRT: Item Response Theory) は 現代テスト理論 とも呼ばる．

因子分析に基づいた古典テスト理論とは異なり，特定の項目に被験者がどのように応答するかを左右する種々の潜在変数を柔軟に取り入れることを可能にする モデルベース の枠組みである．⁶

その柔軟性のため，コンピュータを通じた適応的なテスト などの現代的な設定における心理測定・行動計量の基礎を支えている．

3.2 項目反応理論の歴史

項目反応理論の初まりは (Lord et al., 1968) と ETS における実践・セミナーと目されている．

書籍 (Lord et al., 1968) はテストに対して真に統計的でモデルベースな扱いを創始したと評されている (Embretson and Reise, 2000)．

ただし，同様の取り扱いはデンマークにて (Rasch, 1960) により早くから用いられており，この２つが IRT の源流とされている (Embretson and Reise, 2000)．

(Rasch, 1960) のモデルは２値応答の確率を，個人と項目とのそれぞれ１母数の関数としてモデリングする最も単純なものであった．

長らくこの研究はヨーロッパを出ず，(Fischer, 1973) がこれを拡張し翌年に教科書も書いたが，ドイツ語であったので世界的には広まらなかった．

最終的に２つの流れが邂逅したのは Benjamin Wright を介してであった．

1960 年に Rasch が Wright を訪問して以来，Rasch モデルの客観的測定 (objective measurement properties) の重要性を評価し，その推定方法を FORTRAN により実装した (Wright and Panchapakesan, 1969)．

その後 Wright の下で学んだ多くの学生が (Rasch, 1960) のモデルに関して基礎的な研究を行なった．⁷

3.3 項目反応モデルの応用

項目反応モデルは個々人レベルの応答変数に基づいて，個人ごとに違う潜在変数 \(\theta_i\) と項目ごとに違うパラメータ \(\xi_j\) の推定を実行する際に広く用いられる．

\(\theta_i\) は典型的には個々人の「能力」といった概念構成を表すパラメータで 能力母数 (ability parameter) とも呼ばれる (Fox, 2010, p. 6)．一方 \(\xi_j\) は難易度パラメータ (difficulty parameter) ともいう．

項目反応モデルの用途は主に潜在変数の測定 (measurement) と多次元尺度構成 (scaling) との２つに分けられる．

理想点解析は後者の用途に属する．これはパラメータ \(\theta_i\) がテストの種類などの測定方法に依存せず，モデルが同一ならば一定した尺度を持つという項目反応モデルの美点に基づく．この普遍性を Rasch は 固有客観性 (specific objectivity) と呼んだ (井澤廣行, 2008, p. 51)．

また複数の項目反応モデルの結果の間で尺度を統一することを，特にテスト分析の分野では リンキング または 等化 (equating) という．⁸

3.4 ２値反応の項目反応モデル

項目反応モデルでは \(\theta_i\) は応答確率を変化させるとする： \[ \operatorname{P}[Y_{ij}=1]=g_j(\theta_i),\qquad i\in[N],j\in[J]. \] このリンク関数 \(g_j\) は 項目特性曲線 (ICC: Item Characteristic Curve / Trace Line) と呼ばれる．

加えて \(\theta_i\) の値で条件付けたとき，異なる項目への応用は互いに独立であると仮定する（局所独立性 という）：⁹ \[ \operatorname{P}[Y_{i1}=1,\cdots,Y_{iJ}=1]=\prod_{j=1}^J\operatorname{P}[Y_{ij}=1]. \]

(Rasch, 1960) モデル

１母数応答モデル (1PLM: one-parameter logistic model) または Rasch モデル とは，個人の母数 \(\theta_i\) と項目の母数 \(b_j\) とが定めるロジスティックモデル \[ \operatorname{P}[Y_{ij}=1]=\biggr(1+e^{b_j-\theta_i}\biggl)^{-1} \] である．

\(b_j-\theta_i\) は \(b_j,\theta_i\) 双方の十分統計量であり，\(\theta_i\) のみを条件付き最尤推定可能である．

\(b_j,\theta_i\) は同じ空間 \(\mathbb{R}\) 上にプロットでき，同じ尺度を持つことに注意．\(\theta_i\) が \(b_j\) からみて左右のどちらにあるかに依って，応答確率が \(1/2\) より大きいか小さいかが決まる．

２母数ロジットモデル

２母数ロジットモデル (2PLM: two-parameter logistic model) とは，項目 \(j\in[J]\) が２つの母数 \(a_j,b_j\) でパラメータ付けられたロジスティックモデル \[ \operatorname{P}[Y_{ij}=1]=\biggr(1+e^{b_j-a_j\theta_i}\biggl)^{-1} \] である．\(a_j\) は 項目識別力母数 (item discrimination parameter) ともいう．¹⁰

もはや条件付き最尤推定は不可能であるが，(Bock and Lieberman, 1970) は能力母数を局外母数として項目母数を推定する方法を数値積分法によって与えた．

EM アルゴリズムによる周辺最尤推定法 (Bock and Aitkin, 1981) は能力母数を局外母数と扱う教育の分野において現在でも標準的な方法の１つである．

プロビットモデルも \(n\)-PNM (\(n\)-Parameter Normal ogive Model) (Lord et al., 1968, pp. 365–384) として古くから考えられていたが，Gibbs サンプリングの都合上ロジスティックモデルが好まれた．

ロジスティックモデルで推定された空間上で \(d=1.7\) のスケーリングの違いを除いて [-3,3] 上ではほとんど一致することが知られている (Hambleton, 1991, p. 15)．

3.5 多値項目反応モデル

正解・誤答の２値以外にも，部分点があるなどの多値項目 (polytomous item) に対する拡張が考えられている．

(部分得点モデル Masters, 1982)

部分得点モデル (PCM: Partical Credit Model) (Masters, 1982) とは，項目 \(j\in[J]\) の応答がカテゴリ \(c\in[C_j]\) に当たる確率を \[ \operatorname{P}[Y_{ij}=c]=\frac{e^{\sum_{l=1}^c(\theta_i-\kappa_{kl})}}{\sum_{r=1}^{C_j}e^{\sum_{l=1}^r(\theta_i-\kappa_{kl})}} \] で与える．

\(\kappa_{kl}\) は項目 \(j\in[J]\) の step 難易度パラメータという．

(Muraki, 1992) はこれを一般化し，EM アルゴリズムによる推定方法を与えている．

(段階反応モデル Samejima, 1997)

段階反応モデル (GRM: Graded Response Model) (Samejima, 1997) では，項目 \(j\in[J]\) の応答確率の分布関数をモデリングし，カテゴリ \(c\in[C_j]\) に当たる確率は \[ \operatorname{P}[Y_{ij}=c]=\biggr(e^{\kappa_{j,c-1}-a_j\theta_i}\biggl)-\biggr(e^{\kappa_{j,c}-a_j\theta_i}\biggl) \] で与えられる．

ただし，難易度パラメータには \[ -\infty=\kappa_{j,0}<\kappa_{j,1}<\cdots<\kappa_{j,C_j}=\infty \] という順序制約が必要になる．

3.6 多次元の項目反応モデル

多次元項目反応モデル

\(b_j-a_j^\top\theta_j\) という指標を多次元化することで，(Rasch, 1960) のモデルを多次元化することができる： \[ \operatorname{P}[Y_{ij}=1]=\operatorname{expit}\biggr(-b_j+a_j^\top\theta_i\biggl). \]

空間理論（第 1.2 節）の端緒からして，単なる１次元の左-右といった軸ではなく，多次元の潜在空間上に各政治家の理想点を写像したい，という悲願がある (岡田謙介 and 加藤淳子, 2016)．

このように新たな次元も考慮に入れることで，リベラル - 保守といった概念への理解が進むことが期待される上に，予測などの下流タスクの精度の大きな向上も望めるだろう．

一般に複雑な構成概念の精緻な検証が可能になる (坂本佑太朗 and 柴山直, 2017) ため，多次元項目反応モデルは近年注目されており，これを実現する統計計算法が必要とされている．

特に識別可能性の問題が深刻になるが，それがベイズのアプローチでは，\(\ell_2\)-ノルムベースであったところを \(\ell_1\)-ノルムベースにすることで，推定の安定性と効率性が向上することなどが考えられている (Lim et al., 2024)．

3.7 理想点解析の認知モデリングとしての展開

従来の理想点解析における参照軸は，純粋に複雑な政治的現象を理解するための構成概念として利用された．

一方で理想点解析と項目反応理論との類似性に気付いた以上，応答過程に認知科学的変数も取り入れることは自然な拡張の１つとして試みられてきた (Lee, 2001)．

例えば個々人の認知過程の違い (Embretson (Whitely), 1984) や発達段階の違い (Wilson, 1984) も変数に取り入れることが考えられている．

そこで近年，理想点推定が出力する「次元」に対する人間の空間的認知との関係を明示的に取り入れたモデリングをしようという試みが，行動計量学との接点で考えられている (岡田謙介 and 加藤淳子, 2016)．

4 文献紹介

4.1 政治学と空間理論

(浅古泰史, 2016) は政治学における空間理論の入門として良い．

関連する日本語文献には (細野助博, 1981), (稗田健志, 2015) などがある．

NOMINATE 関連については (Poole and Rosenthal, 2001), (Poole and Rosenthal, 2007) を参考にした．

4.2 項目反応理論

主に (Embretson and Reise, 2000), (Fox, 2010) を参照した．

項目反応理論の日本語文献には (前川眞一, 2023), (山口一大, 2022) が良い．

(井澤廣行, 2008) が Rasch の歴史に詳しい．

References

Albert, J. H. (1992). Bayesian estimation of normal ogive item response curves using gibbs sampling. Journal of Educational Statistics, 17(3), 251–269.

Bafumi, J., Gelman, A., Park, D. K., and Kaplan, N. (2005). Practical issues in implementing and understanding bayesian ideal point estimation. Political Analysis, 13(2), 171–187.

Bakker, R., and Poole, K. T. (2013). Bayesian metric multidimensional scaling. Political Analysis, 21(1), 125–140.

Barberá, P. (2015). Birds of the same feather tweet together: Bayesian ideal point estimation using twitter data. Political Analysis, 23(1), 76–91.

Black, D. (1948). On the rationale of group decision-making. Journal of Political Economy, 56(1), 23–34.

Bliss, C. I. (1934). The method of probits. Science, 79(2037), 38–39.

Bock, R. D., and Aitkin, M. (1981). Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 46(4), 443–459.

Bock, R. D., and Lieberman, M. (1970). Fitting a response model forn dichotomously scored items. Psychometrika, 35(2), 179–197.

Carroll, R., Lewis, J. B., Lo, J., Poole, K. T., and Rosenthal, H. (2009). Measuring bias and uncertainty in DW-NOMINATE ideal point estimates via the parametric bootstrap. Political Analysis, 17(3), 261–275.

Clinton, J. D., Jackman, S., and Rivers, D. (2004). The statistical analysis of roll call data. American Political Science Review, 98(2), 355–370.

Clinton, J. D., and Meirowitz, A. (2001). Agenda constrained legislator ideal points and the spatial voting model. Political Analysis, 9(3), 242–259.

Clinton, J. D., and Meirowitz, A. (2017). Integrating voting theory and roll call analysis: A framework. Political Analysis, 11(4), 381–396.

Converse, P. E. (2006). The nature of belief systems in mass publics (1964). Critical Review, 18(1-3), 1–74.

Davis, O. A., Hinich, M. J., and Ordeshook, P. C. (1970). An expository development of a mathematical model of the electoral process. The American Political Science Review, 64(2), 426–448.

Downs, A. (1957). An economic theory of democracy. New York: Harper & Row.

Embretson, S. E., and Reise, S. P. (2000). Item response theory for psychologists. Psychology Press.

Embretson (Whitely), S. (1984). A general latent trait model for response processes. Psychometrika, 49(2), 175–186.

Enelow, J. M., and Hinich, M. J. (1984). The spatial theory of voting: An introduction. Cambridge University Press.

Escolar, E. G., Hiraoka, Y., Igami, M., and Ozcan, Y. (2023). Mapping firms’ locations in technological space: A topological analysis of patent statistics. Research Policy, 52(8), 104821.

Fischer, G. H. (1973). The linear logistic test model as an instrument in educational research. Acta Psychologica, 37(6), 359–374.

Fox, J.-P. (2010). Bayesian Item Response Modeling. Springer New York.

Gelman, A. (2014). How Bayesian Analysis Cracked the Red-State, Blue-State Problem. Statistical Science, 29(1), 26–35.

Hambleton, S., R. K. (1991). Fundamentals of item response theory. Sage Publications.

Hansen, B. E. (2022). Econometrics. Princeton University Press.

Heckman, J. J., and Snyder, J. M. (1997). Linear probability models of the demand for attributes with an empirical application to estimating the preferences of legislators. The RAND Journal of Economics, 28, S142–S189.

Hinich, M. J., and Pollard, W. (1981). A new approach to the spatial theory of electoral competition. American Journal of Political Science, 25(2), 323–341.

Hotelling, H. (1929). Stability in competition. The Economic Journal, 39(153), 41–57.

Imai, K., Lo, J., and Olmsted, J. (2016). Fast Estimation of Ideal Points with Massive Data. American Political Science Review, 110(4), 631–656.

Jackman, S. (2000). Estimation and inference are missing data problems: Unifying social science statistics via bayesian simulation. Political Analysis, 8(4), 307–332.

Jackman, S. (2001). Multidimensional analysis of roll call data via bayesian simulation: Identification, estimation, inference, and model checking. Political Analysis, 9(3), 227–241.

Klein, R. W., and Spady, R. H. (1993). An efficient semiparametric estimator for binary response models. Econometrica, 61(2), 387–421.

Lee, M. D. (2001). Determining the dimensionality of multidimensional scaling representations for cognitive modeling. Journal of Mathematical Psychology, 45(1), 149–166.

Lewis, J. B., and Poole, K. T. (2004). Measuring bias and uncertainty in ideal point estimates via the parametric bootstrap. Political Analysis, 12(2), 105–127.

Lim, J., Shin, S., and Park, J. H. (2024). \(\ell^1\)-based bayesian ideal point model for multidimensional politics. In ISI world statistics congress,Vol. 64.

Lord, F. M., Novick, M. R., and Birnbaum, A. (1968). Statistical Theories of Mental Test Scores. Addison-Wesley.

Lunn, D. J., Thomas, A., Best, N., and Spiegelhalter, D. (2000). WinBUGS - a bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing, 10(4), 325–337.

MacRae, D. (1958). Dimensions of congressional voting: A statistical study of the house of representatives in the eighty-first congress. University of California Press.

Martin, A. D., and Quinn, K. M. (2002). Dynamic ideal point estimation via markov chain monte carlo for the u.s. Supreme court, 1953–1999. Political Analysis, 10(2), 134–153.

Masters, G. N. (1982). A rasch model for partial credit scoring. Psychometrika, 47(2), 149–174.

McCarty, N. M., Poole, K. T., and Rosenthal, H. (1997). Income Redistribution and the Realignment of American Politics. AEI Press.

McFadden, D. L. (1976). Quantal Choice Analysis: A Survey. In Annals of Economic and Social Measurement, Volume 5, number 4, pages 363–390. National Bureau of Economic Research, Inc.

Miwa, H., and Taniguchi, M. (2017). Heterogeneity in voter perceptions of party competition in multidimensional space: Evidence from japan. International Political Science Review, 38(5), 673–689.

Muraki, E. (1992). A Generalized Partial Credit Model: Application of an EM Algorithm. ETS Research Report Series, 1992(1), i–30.

Poole, K. T., Lewis, J. B., Lo, J., and Carroll, R. (2011). Scaling roll call votes with wnominate in r. Journal of Statistical Software, 42(14), 1–21.

Poole, K. T., and Rosenthal, H. (1985). A spatial model for legislative roll call analysis. American Journal of Political Science, 29(2), 357–384.

Poole, K. T., and Rosenthal, H. (1991). Patterns of congressional voting. American Journal of Political Science, 35(1), 228–278.

Poole, K. T., and Rosenthal, H. (1997). Congress: A Political-Economic History of Roll Call Voting. New York: Oxford University Press.

Poole, K. T., and Rosenthal, H. (2001). D-nominate after 10 years: A comparative update to congress: A political-economic history of roll-call voting. Legislative Studies Quarterly, 26(1), 5–29.

Poole, K. T., and Rosenthal, H. (2007). Ideology and congress: A political economic history of roll call voting. Routledge.

Rasch, G. W. (1960). Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests. Nielsen & Lydiche.

Samejima, F. (1997). Graded response model. In W. J. van der Linden and R. K. Hambleton, editors, Handbook of modern item response theory, pages 85–100. New York, NY: Springer New York.

Simonson, I. (1989). Choice based on reasons: The case of attraction and compromise effects. Journal of Consumer Research, 16(2), 158–174.

Singh, G., Memoli, F., and Carlsson, G. (2007). Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition . In M. Botsch, R. Pajarola, B. Chen, and M. Zwicker, editors, Eurographics symposium on point-based graphics. The Eurographics Association.

Wilson, M. R. (1984). A psychometric model of hierarchical development (PhD thesis). University of Chicago.

Wright, B., and Panchapakesan, N. (1969). A procedure for sample-free item analysis. Educational and Psychological Measurement, 29(1), 23–48.

Zeileis, A., Kleiber, C., and Jackman, S. (2008). Regression models for count data in R. Journal of Statistical Software, 27(8).

三輪洋文. (2017). Twitter データによる日本の政治家・言論人・政党・メディアのイデオロギー位置の推定. 選挙研究, 33(1), 41–56.

井澤廣行. (2008). Raschの理論と理念、及び、WrightのRasch測定展開. In,Vol. 20.

前川眞一. (2023). 項目反応理論におけるモデル変換. 日本テスト学会誌, 19(1), 35–58.

加藤拓巳. (2021). 選択における文脈効果の出現要因とその方向性. マーケティングジャーナル, 40(3), 78–88.

加藤淳子. (2021). 政党の政策位置についての専門家調査.

坂本佑太朗, and 柴山直. (2017). 学力テストの下位領域に関する多次元IRT分析. データ分析の理論と応用, 6(1), 31–45.

宇佐美慧, 荘島宏二郎, 光永悠彦, and 登藤直弥. (2018). 項目反応理論（IRT）の考え方と実践. 日本教育心理学会総会発表論文集, 60, 24–25.

山口一大. (2022). 項目反応理論モデルのパラメタ推定法の展開. 日本テスト学会誌, 18(1), 103–131.

岡田謙介, and 加藤淳子. (2016). 政治学における空間分析と認知空間. 行動計量学, 43(2), 155–166.

林光. (2016). 新しい外交による国際制度形成の理論と実証 (PhD thesis). 東京大学. Retrieved from https://doi.org/10.15083/00074976

浅古泰史. (2016). 政治の数理分析入門. 木鐸社.

稗田健志. (2015). 政治理論と実証研究をつなぐ環. 年報政治学, 66(1), 1_13–1_36.

細野助博. (1981). 政治競争モデル設計の試み. 公共選択の研究, 1981(1), 65–73.

飽戸弘. (1966). 政治的態度の構造に関する研究 i. 心理学研究, 37(4), 204–218.

Footnotes

1. (浅古泰史, 2016, p. 69) を参考．

2. (浅古泰史, 2016, p. 75) を参考．

3. この交渉理論におけるコンテクストから，理想点 というのである．各主体が理想とする点，という意味である．

4. “In short, the goal that Bayesian methods make plausible is a transformation of roll call analysis, from a technical scaling or measurement problem best left to psychometricians (witness the canonical status of NOMINATE scores) to something that scholars motivated primarily by substantive concerns can do for themselves.” (Jackman, 2001, p. 240)．

5. probit とは (Bliss, 1934) が probability unit から名付けた．

6. 例えば消費者の購買行動をモデリングする際は，選択疲れをした消費者は中間的な商品を選びやすいという 妥協効果 (compromise effect) (Simonson, 1989) などの文脈効果もモデルに入れる必要がある (加藤拓巳, 2021)．

7. だが，Bock も Wright の教え子も主に教育学で活躍しており，最終的に心理学者に心理測定の基本として古典テスト理論を IRT が代替したのは 2000 年代になってからだったという (Embretson and Reise, 2000, p. 7)．

8. ２つは厳密には，等化は一番強い仮定のもとで行われるリンキングの一つである (宇佐美慧 et al., 2018)．例えば集団の基礎学力が違った場合，同一の困難度を測定するためでも別のバージョンのテストを作成する必要がある．等化は ICC が affine 合同である場合に affine 変換により可能である (宇佐美慧 et al., 2018)．

9. これが成り立つように，１つの設問で問われる能力は１つになるように設計することが原則である (宇佐美慧 et al., 2018)．

10. ３母数ロジットモデルにおいて加わる母数は当て推量母数／下方漸近パラメータとも呼ばれる (宇佐美慧 et al., 2018)．