階層ベイズ理想点解析

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

1 前稿

2 モデル

2.1 構造

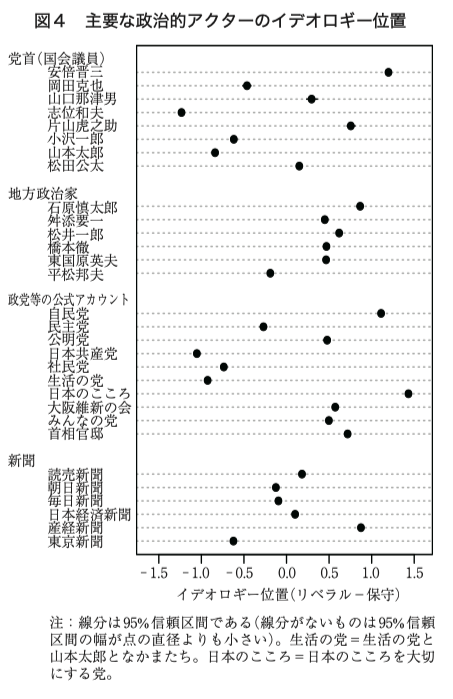
議会での点呼投票データ \(\{Y_{i,j}\}_{i\in[N],j\in[J]}\) を考える．２母数ロジットモデル \[ \operatorname{P}[Y_{i,j}=1]=\Phi(\alpha_j+\beta_jX_i) \tag{1}\] によって各議員 \(i\in[N]\) の理想点 \(X_i\in\mathbb{R}\) を推定することを考える．さらにここに階層モデル \[ X_i=Z_i^\top\gamma_{g(i)}+\epsilon_i,\qquad\epsilon_i\sim\mathrm{N}(0,\sigma^2), \tag{2}\] を考える．ただし \(Z_i\in\mathbb{R}^p\) は議員ごとの共変量， \[ g:[N]\to[G] \] は議員の項目応答特性のクラスタリングとする．

2.2 事前分布

第一階層 (1) の２母数ロジットモデルには \[ \alpha_j\sim\mathrm{N}(0,\sigma_\alpha^2),\quad\beta_j\sim\mathrm{N}(0,\sigma_\beta^2) \] という正規事前分布を仮定する．

第二階層 (2) の共変量にはスパース性を促進する spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) を仮定する： \[ p(d\gamma_{g(i)})=\omega_{g(i)}\delta_0(d\gamma_{g(i)})+(1-\omega_{g(i)})p_0(d\gamma_{g(i)}). \] \[ \omega_{g(i)}\sim\operatorname{Beta}(a,b). \] ただし \(p_0\) は多様な理想点を促進するために t-分布とする．

\(\sigma\) には half-Cauchy 事前分布を仮定する： \[ \sigma\sim\text{Half-Cauchy}(0,1). \]

最後にグループ所属 \(g\) には，最大クラスタ数 \(G_\max=10\) を仮定し， \[ \operatorname{P}[g(i)=g]=\frac{1}{G},\qquad G\sim U([G_\max]) \] とする．

3 計算

モデル (1), (2) の尤度 \[ p(y_{ij}|z_i,\alpha_j,\beta_j,\gamma_g,g,\sigma) \] は \(g\) に関してのみ微分可能でない．

そこで基本的には \(\gamma\in\mathbb{R}^p\) と \(\alpha_j,\beta_j\in\mathbb{R},\sigma\in\mathbb{R}_+\) のサンプリングには Sticky PDMP サンプラー (Chevallier et al., 2023), (Bierkens et al., 2023) を用い，\(g\in [G]^{[N]}\) のサンプリングには次の２つの時計を追加して行う： \[ \Lambda^S(t):=\Lambda_0^S\left(1\land\frac{p(g')}{p(g)}\right), \] \[ \Lambda^K(t)=\Lambda_0^K. \]

\(\Lambda^S\) により候補 \(g'\in [G]^{[N]}\) への遷移を行い，\(\Lambda^K\) により候補 \(g'\in [G]^{[N]}\) の更新をある確率核 \(q_g(g,-)\) に従って行う．

広大な離散空間 \([G]^{[N]}\) 上を Poisson 跳躍により歩き回る．これは Zig-Zag within Gibbs (Sachs et al., 2023), (Hardcastle et al., 2024) の考え方である．

References

Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Chevallier, A., Fearnhead, P., and Sutton, M. (2023). Reversible jump PDMP samplers for variable selection. Journal of the American Statistical Association, 118(544), 2915–2927.

Hardcastle, L., Livingstone, S., and Baio, G. (2024). Averaging polyhazard models using piecewise deterministic monte carlo with applications to data with long-term survivors.

Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.

Sachs, M., Sen, D., Lu, J., and Dunson, D. (2023). Posterior Computation with the Gibbs Zig-Zag Sampler. Bayesian Analysis, 18(3), 909–927.