数学者のためのカーネル法概観

概要

数学者のために，カーネル法によるデータ解析が何をやっているのかを抽象的に説明する．カーネルとは対称な２変数関数であり，これを用いてデータ点を，データ空間上の関数に変換することで非線型変換を獲得するための道具である．

1 導入

カーネル法とは，非線型な前処理を施すことで，その後の線型なデータ解析の性能を向上させるための手法であると言える．

これはニューラルネットワークと違いカーネル関数を決める段階が必要がある一方で，無限次元の特徴空間（再生核 Hilbert 空間）上の表現を得ることが出来るという美点がある．

1.1 データの非線型変換

線型手法が使えないときに，変数変換を挟むことで線型分離可能な問題に還元するという手法は広く見られる．

1.1.1 Box-Cox 変換

例えば，データが正規分布から大きく違っている場合，Box-Cox 変換 (Box and Cox, 1964)

\[ x \longmapsto x^{(\lambda)} = \begin{cases} \displaystyle \frac{x^\lambda - 1}{\lambda} & \lambda \neq 0\\ \log x & \lambda = 0\end{cases} \]

を通じて正規分布に近づけることが出来る．$\lambda\in\mathbb{R}$ をハイパーパラメータとしてデータから調整出来る．

Box-Cox 変換は特定のリンク関数 $G$ に関する一般化線型モデルと見れる．¹

1.1.2 カーネル法

Box-Cox 変換はカーネル法もこのような非線形変換を見つけてくるための統一的な方法論である．

カーネル法によってデータを非線型変換をして得る空間は 特徴空間 と呼ばれ，この上で従来の線型なデータ解析を施すだけで，全体としては非線型な手法の完成である．

1.2 カーネル法の歴史

1992年，当時は2023年に生きる我々と全く同じく，ニューラルネットワーク（以降NN）のブームのさなかにあった（当時は第二期ブーム）．このブームを一度終わらせたのが，(Boser et al., 1992) によるカーネル法であった．

当時は数学の範疇から出たことがなかったカーネルの概念を用いて，SVMを非線形化したKernel SVMという手法を提案したのである．以降，非線形問題を扱えるモデルとして，NNを凌ぐ勢いで発展し，NNがvanishing gradientsという障壁にぶつかったこともあり，2000年から2006年を「深層学習の冬」とまで言わしめた．

1.3 カーネル法の課題

2006年というのは，(Hinton et al., 2006), (Hinton and Salakhutdinov, 2006) の年である．この自己符号化器の発表がきっかけになり，DNNの訓練がますます効率的になり，一方でKernel SVMは次の2つの障壁に直面しており，現在のDNN最強の時代を我々は見ている．²

種々のタスクに対して，最適なカーネルが何かがわかっていない．
データ数が多すぎると実行不可能になる．

カーネル法のトリックは単純であるから，個々の問題に即したカーネルの選び方，または適応的にカーネルを定めるアルゴリズムのデザインが，今後の課題である．

2 カーネル法の数理

2.1 カーネル法の骨格

カーネルと言ったとき，数学的には「（実数値の）半正定値対称関数」を指す．

定義：（実数値の）正定値カーネル

関数 $k:\Omega\times\Omega\to\mathbb{R}$ が正定値カーネルであるとは，次の２条件を満たすことをいう：

対称性：$k(x,y)=k(y,x)$．
正値性：任意有限個の点 $x_1,\cdots,x_n\in\Omega$ に対し，行列 $\bigl(k(x_i,x_j)\bigr)^n_{i,j=1}$ は半正定値：³ \[ \sum_{i,j=1}^nc_ic_jk(x_i,x_j)\ge0,\qquad c_i\in\mathbb{R}. \]

例：$\Omega=\mathbb{R}^d$ 上の正定値カーネル

Euclid内積：$k(x,y)=x^\top y$．
Gaussカーネル：$k_G(x,y)=\exp\left(-\frac{1}{2\sigma^2}\|x-y\|^2\right)\;(\sigma>0)$．
Laplaceカーネル：$k_L(x,y)=\exp\left(-\alpha\sum_{a=1}^d|x_a-y_a|\right)\;(\alpha>0)$．
多項式カーネル：$k_P(x,y)=(c+x^\top y)^d\;(c\ge0,d\in\mathbb{N})$．

この「正定値カーネル」の概念は，次の意味で，「内積」と同一視できる．「内積」と同一視できるという意味で，「類似度の測り方」に対応する．

定理：Moore-Aronszajn 1950

任意の集合 $\Omega$ 上の正定値カーネル $k$ に対して，$\Omega$ 上の関数からなるHilbert空間 $H_k$ であって，以下を満たすものが一意に定まる：⁴

$k(-,x)\in H_k\;(\forall_{x\in\Omega})$．
（再生性）$(f\,|\,k(-,x))_{H_k}=f(x)$．

このHilbert空間 $H_k$ を数学では $k$-再生核Hilbert空間といい，データ解析では $k$-特徴空間という．

ここで，数学概念について，少し突飛に思えるかもしれないが，次の名前をつける．

定義

正定値カーネル $k:\Omega\to\mathbb{R}$ について，

$x\mapsto k(-,x)$ という対応 $\Phi:\Omega\to H_k$ を特徴写像という．
$\Phi$ は「内積を保つ」が，この性質をカーネルトリックという： \[ \left(\Phi(x)\,\middle|\,\Phi(y)\right)_{H_k}=k(x,y). \]

「特徴写像」は，データ $x,y\in\Omega$ を正定値カーネルが測る「類似度」を変えないように，しかしながら全く違う空間内の点 $\Phi(x),\Phi(y)\in H_k$ に写している．「類似度」が変わっていないことを「カーネルトリック」と呼ぶ．

この「トリック」は少し米田埋め込みに似ている．データ $x\in\Omega$ の他のデータとの類似度の全体 $k(-,x):\Omega\to\mathbb{R}$ は，そのデータを特徴づけるのである $k(-,x)=\Phi(x)\in H_k$．

また，関数のなすHilbert空間 $H\subset\mathbb{R}^\Omega$ が， $\{\mathrm{ev}_x\}_{x\in\Omega}\subset H^*$ を満たすならば，$H$ は再生核を持つ．このような関数空間 $H$ の内積の構造を $\Omega$ にも導入したいとき， $k$ を通じてすれば良いということになる． $k$ は違う $H_k$ と $\Omega$ を対応づけ，正しい $k$ を選ぶと，データ $\{x_1,\cdots,x_n\}\subset\Omega$ のうちなる「特徴」を暴き出せるかもしれない．

2.2 カーネル法の強み

こうして見たように，カーネル法は

非線型な情報，特に高次モーメントの扱いができる．
データの次元 $X_i\in\mathbb{R}^p$ に依らない．が，データ数 $N$ に依存し，次元の呪いを受ける．
データの形式にも依らない．ベクトルでなくとも，グラフでも，行列でも，分布でも良い．

3 種々のデータ解析のカーネル化

3.1 データ解析のやり方

カーネル $k$ を用意する．すると，特徴空間 $H_k$ が定まるが，これは一般に関数空間であり，無限次元である．$H_k$ の元を「特徴ベクトル」と言ったりするのに，その正体は関数である．
カーネルトリック（≒再生性）が，「特徴ベクトル同士の内積」だけを計算可能にする．

要は計算できることは内積だけなのである！しかし，特徴写像や特徴ベクトルの表示を陽に使わずとも，内積だけで実行可能な線型データ解析は，実に多いのである．

3.2 例：Ridge回帰

Ridge回帰は，次の最適化によって線型回帰係数 $a\in\mathbb{R}^p$ を推定するロバスト手法である：

\[ \min_{a\in\mathbb{R}^p}\frac{1}{n}\sum_{i=1}^n(Y_i-a^\top X_i)^2+\lambda\|a\|^2. \]

これを「カーネル化する」とは，「特徴空間で実行する」ということである． $X_i$ の代わりに $\Phi(X_i)$ 上で，Euclid内積 $a^\top X_i$ の代わりに特徴空間の内積 $(f|\Phi(X_i))_{H_k}$ で実行するということである：

\[ \min_{f\in H_k}\frac{1}{n}\sum_{i=1}^n\biggl(Y_i-(f|\Phi(X_i))_{H_k}\biggr)+\lambda\|f\|^2_H \]

実はこの式は次と等価：

\[ \min_{f\in H_k}\frac{1}{n}\sum_{i=1}^n\biggl(Y_i-f(X_i)\biggr)+\lambda\|f\|^2_H \]

たしかに，$f\in H$ は一般の関数であり，非線形な回帰を行なっていることになる！

しかし，最後にこの最適化問題をどう解くか？という問題が残り，無限次元空間 $H$ 上での最適化の理論が必要になるかといえばそうではなく，

\[ f=f_\Phi:=\sum_{i=1}^nc_i\Phi(X_i) \]

という形のみで解を探せば良いことが判る．これは $f=f_\Phi\oplus f_\perp$ という直交分解を考えることで従う．つまり，最適化はデータ点 $\Phi(X_1),\cdots,\Phi(X_n)$ の張る有限次元部分空間上のみで考えれば良い．この事実には representer 定理 (Kimeldorf and Wahba, 1970), (Schölkopf et al., 2001) という名前がついている．

すると目的関数は

\[ \frac{1}{N}\sum_{i=1}^N\biggl(Y_i-\sum_{j=1}^Nc_jk(X_i,X_j)\biggr)^2+\lambda\underbrace{\sum_{i,j=1}^Nc_ic_jk(X_i,X_j)}_{=c^\top Kc} \]

となり，これを解くと，カーネルRidge回帰の解は

\[ \widehat{f}(x)=\boldsymbol{k}(x)^\top(K+n\lambda_nI_n)^{-1}\boldsymbol{Y}, \]

\[ \boldsymbol{k}(x)=\begin{pmatrix}k(x,X_1)\\\vdots\\k(x,X_N)\end{pmatrix},\boldsymbol{Y}=\begin{pmatrix}Y_1\\\vdots\\Y_N\end{pmatrix} \]

と表せることがわかる．

3.3 発展

第 1.2 節で紹介した2つの問題点に戻る．

種々のタスクに対して，最適なカーネルが何かがわかっていない．
データ数が多すぎると実行不可能になる．

この2.について，カーネルRidge回帰の例だと，逆行列 $$(K+n\lambda_nI_n)^{-1}$ の計算が実行不可能になるという形で現前する．しかし，Woodburyの公式から，低ランク近似が得られていれば，それを活用できる．一般にGram行列の固有値の減衰は速いことが知られており，この低ランク近似の戦略は筋が良いと言える．

1.について，まずSVMなどの教師あり学習の設定では，CVを使うことでカーネル選択をすることができる．が，教師なし学習では一般的な方法はない．特にカーネル主成分分析（次節の例）．しかし，これを適応的に学習するというのは良いアイデアだろう．Multiple Kernel Learning (Gönen and Alpaydin, 2011) はカーネルの凸結合を学習し，Deep Kernel Learning (Wilson et al., 2016) はNNによってカーネルを学習する．

3.4 例：主成分分析

主成分分析を抽象的に理解すれば，分散が大きい方向に射影をすることで，「意味がある方向」を見つける手法なのであった．

主成分方向とは

\[ \max_{a\in\mathbb{R}^p:\|a\|=1}\sum_{i=1}^N(a^\top(X_i-\overline{X}))^2. \]

の解 $a\in\mathbb{R}^p$ である．これは分散共分散行列の固有値問題を解くことに等価になる．

この手法を「カーネル化」するには，特徴空間で実行すれば良い．

\[ \max_{f:\|f\|_H=1}\sum_{i=1}^N\biggl(f\,\bigg|\,\Phi(X_i)-\overline{\Phi}(X)\biggr)^2 \]

この解も，データの特徴ベクトルの張る有限部分空間内で調べれば十分なのである！というのも，正確には，平均を引いた次の形のみを考えれば良いことが判る：

\[ f=\sum_{i=1}^Nc_i\biggl(\Phi(X_i)-\overline{\Phi(X)}\biggr) \]

実際には，中心化Gram行列の固有値問題に帰着する：

\[ \widetilde{K}_{ij}=k(X_i,X_j)-\frac{1}{N}\sum_{b=1}^Nk(X_i,X_b)\qquad\qquad \]

\[ \qquad\qquad-\frac{1}{N}\sum_{a=1}^Nk(X_a,X_j)+\frac{1}{n^2}\sum_{a,b=1}^Nk(X_a,X_b). \]

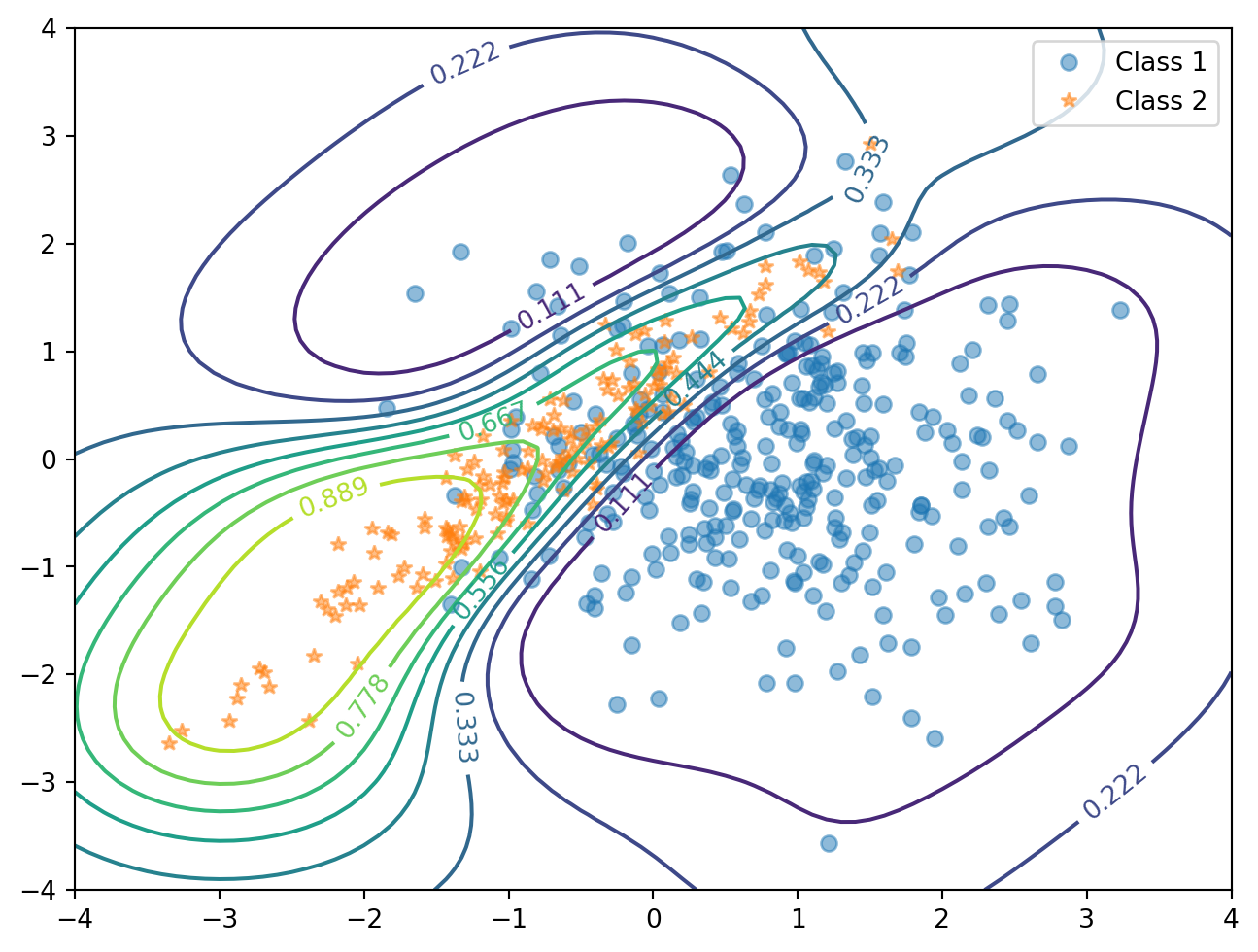
3.5 例：SVM

データ $\{x_1,\cdots,x_n\}\subset\mathbb{R}^p$ が線型分離可能であるとき，ハードマージン法と呼ばれる手法を用いて，これを分離する最大マージン超平面 \[ H_\mathrm{max}:=\operatorname*{argmax}_{H\subset\mathbb{R}^p}\min_{1\le i\le n}d(x_i,H) \] を，凸二次計画問題を解くことによって見つけることができる．このとき，最大のマージンを達成する \[ d(x_{j},H)=\min_{1\le i\le n}d(x_i,H) \] ときの $x_j$ （複数あり得る）をサポートベクトル といい，これが解 $H_{\text{max}}$ を特徴付ける．

この問題において，特徴写像 $\Phi:\mathbb{R}^p\to H_k$ を考えても，やはり解を $n$ 次元部分空間 \[ v\in\left\{\sum_{j=1}^nc_j\Phi(x_j)\in H_k\;\middle|\;c_j\in\mathbb{R}\right\} \] 上で考えれば良いから， \[ \underset{v,\gamma}{\text{minimize}}\quad\|v\|^2_{H_k}=\sum_{i,j=1}^nc_ic_jk(x_i,x_j) \] \[ \text{subject to}\quad\lambda_i\left(\sum_{j=1}^nc_jk(x_i,x_j)+\gamma\right)\ge1\quad(i\in[n]) \] という，やはり凸二次計画問題を解けば良い．

3.6 文献紹介

まとめ

典型的には，線型手法の目的関数が $(\Phi(X_i)|\Phi(X_j)),(f|\Phi(X_i))$ で表現され，さらに解がデータ数の次元を持った有限次元部分空間で見つかる．その結果，Gram行列の解析に帰着し，データ数 $n$ に依存するが，個々のデータの形式に依らない！データはベクトルでなく，カーネルが定義できさえすれば，確率分布自体でも問題がない．

歴史と題した第 1.2 節は (Ghojogh et al., 2021) も参考にした．

References

Aronszajn, N. (1950). Theory of reproducing kernels. Transactions of the American Mathematical Society, 68(3), 337–404.

Boser, B. E., Guyon, I. M., and Vapnik, V. N. (1992). A training algorithm for optimal margin classifiers. In Proceedings of the fifth annual workshop on computational learning theory, pages 144–152.

Box, G. E. P., and Cox, D. R. (1964). An analysis of transformations. Journal of the Royal Statistical Society. Series B (Methodological), 26(2), 211–252.

Ghojogh, B., Ghodsi, A., Karray, F., and Crowley, M. (2021). Reproducing kernel hilbert space, mercer’s theorem, eigenfunctions, nyström method, and use of kernels in machine learning: Tutorial and survey.

Gönen, M., and Alpaydin, E. (2011). Multiple kernel learning algorithms. Journal of Machine Learning Research, 12(64), 2211–2268.

Hinton, G. E., Esindero, S., and Teh, Y.-W. (2006). A fast learning algorithm for deep belief nets. Naural Computation, 18(7), 1527–1554.

Hinton, G. E., and Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313(5786), 504–507.

Kimeldorf, G. S., and Wahba, G. (1970). A correspondence between bayesian estimation on stochastic processes and smoothing by splines. The Annals of Mathematical Statistics, 41(2), 495–502.

Schölkopf, B., Herbrich, R., and Smola, A. J. (2001). A generalized representer theorem. In D. Helmbold and B. Williamson, editors, Computational learning theory, pages 416–426. Berlin, Heidelberg: Springer Berlin Heidelberg.

Tarzanagh, D. A., Li, T., Thrampoulidis, C., and Oymak, S. (2023). Transformers as support vector machines.

Wilson, A. G., Hu, Z., Salakhutdinov, R., and Xing, E. P. (2016). Deep kernel learning. Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, 51, 370–378.

Wolfgang Härdle, M. M., Axel Werwatz, and Sperlich, S. (2004). Nonparametric and semiparametric models. Springer Berlin, Heidelberg.

Footnotes

(Wolfgang Härdle and Sperlich, 2004, p. 162)↩︎
一方でここにきて，現代におけるDNNの最先端とも言えるTransformerをSVMとみなせる，という報告も出てきた (Tarzanagh et al., 2023)↩︎
このようにして構成される行列をGram行列と呼ぶ．↩︎
(Aronszajn, 1950) 参照．↩︎