グラフニューラルネットワーク

概要

グラフニューラルネットワークは CNN や Transformer などの従来のニューラルネットワークアーキテクチャを拡張したクラスである．

1 はじめに

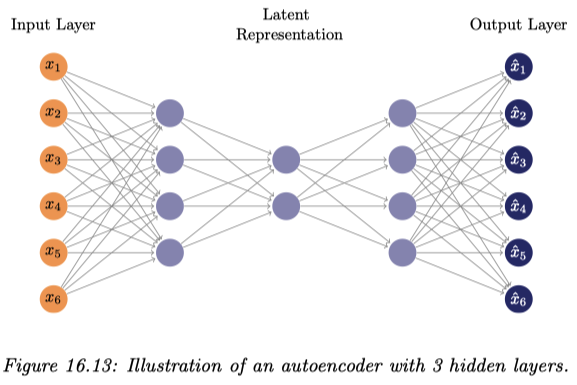
GNN では，通常のニューラルネットワークの最初と最後に，グラフのためのエンコーダーとデコーダーを追加したものと見ることができる．

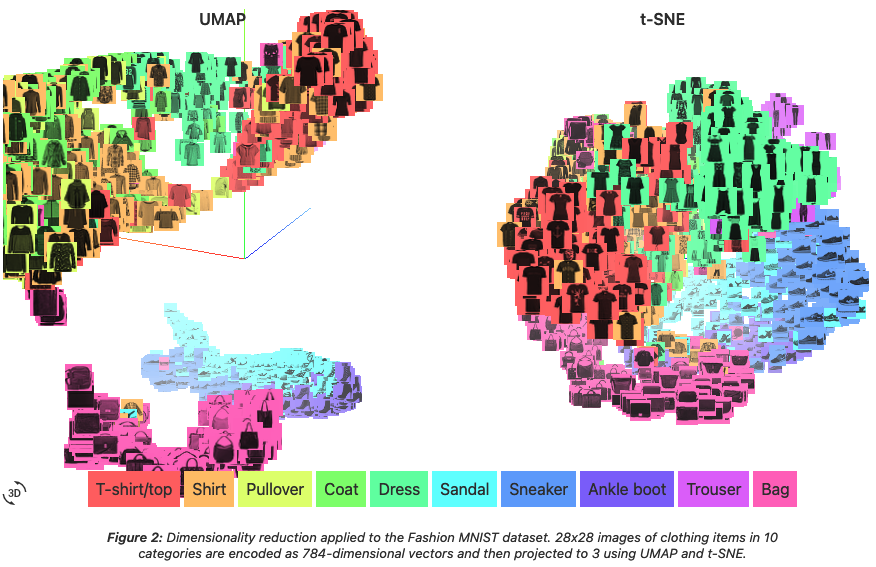
このエンコーダーは，グラフ上でメッセージ伝搬アルゴリズム (aggregation と呼ばれる) を実行することでグラフの局所構造を捉えた特徴抽出をする役割がある．すなわち，同時にグラフ埋め込みタスクも解いている．

CNN の畳み込みも，Transformer の注意機構も，aggregation とみれるという．

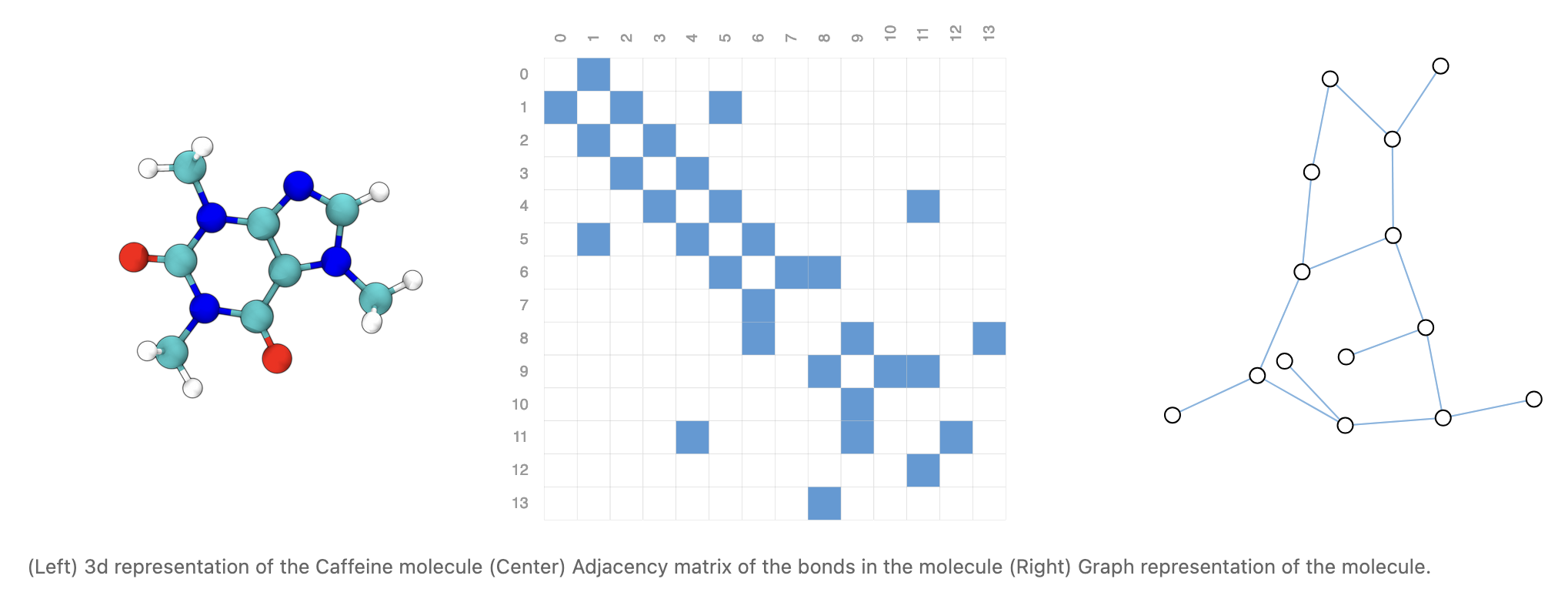
Molecules as Graphs; from (Sanchez-Lengeling et al., 2021)

2 Message Passing GNN

2.1 はじめに

最初のグラフニューラルネットワークは (Gori et al., 2005), (Scarselli et al., 2009) によって提案された．

これはグラフ上で情報を拡散させ，平衡に至るまで待ち，最終的に得られた値をグラフの埋め込みとして，デコーダーで後続タスクを解いているものと見れる．

2.2 メッセージ伝搬

(Gilmer et al., 2017) は既存のグラフに対するニューラルネットワークを統合する枠組み MPNN (Message Passing Neural Networks) を提案し，分子の性質予測の問題に応用した．

(Battaglia et al., 2018) は同時期のサーベイである．

3 スペクトルベースの方法

3.1 スペクトル CNN

(Bruna et al., 2014) では，グラフデータの Laplacian を計算し，これを用いて CNN に繋げる方法を提案した．

3.2 グラフ畳み込みネットワーク (GCN)

グラフの Laplacian を計算するというステップを，ニューラルネットワークと別に用意している点は大変融通が効かない．

そこで Graph Convolutional Network (Kipf and Welling, 2017) が提案された．

4 グラフ畳み込み

スペクトルはグラフの全体から計算する必要があり，グラフのサイズに関してスケールしない．そこで，局所的な情報のみを用いた方法が志向された．

4.1 近傍サンプリング

GraphSAGE (Sample and Aggregate) (Hamilton et al., 2017) は隣接する頂点をサンプリングし，近傍の情報を集める．

これはグラフ Laplaceian をサンプリングにより近似しているともみなせる．

4.2 注意機構

サンプリングをする代わりに，どの近傍点に注目すれば良いかも学習するようにしたのが GAT (Graph Attention Network) (Veličković et al., 2018) である．

4.3 幾何学ベースのアプローチ

Geodesic CNN (Masci et al., 2015) や Anisotropic CNN (Boscaini et al., 2016) など，CNN 分野で蓄積していた幾何学的手法を，グラフに対して応用することを考えたのが MoNet (Monti et al., 2017) である．

一方で，階層構造を持つグラフに対しては Hyperbolic GCN (Chami et al., 2019) や Hyperbolic GNN (Liu et al., 2019) は双曲幾何の応用が考えられている．

5 文献紹介

GNN については，Distill による最高のインタラクティブな解説 (Sanchez-Lengeling et al., 2021) がある．

位相的機械学習に関しては，こちらの稿も参照．

References

Battaglia, P., Hamrick, J. B. C., Bapst, V., Sanchez, A., Zambaldi, V., Malinowski, M., … Pascanu, R. (2018). Relational inductive biases, deep learning, and graph networks. arXiv.

Boscaini, D., Masci, J., Rodolà, E., and Bronstein, M. (2016). Learning shape correspondence with anisotropic convolutional neural networks. In D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, and R. Garnett, editors, Advances in neural information processing systems,Vol. 29. Curran Associates, Inc.

Bruna, J., Zaremba, W., Szlam, A., and LeCun, Y. (2014). Spectral networks and locally connected networks on graphs. In International conference on learning representation.

Chami, I., Ying, Z., Ré, C., and Leskovec, J. (2019). Hyperbolic graph convolutional neural networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. dAlché-Buc, E. Fox, and R. Garnett, editors, Advances in neural information processing systems,Vol. 32. Curran Associates, Inc.

Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., and Dahl, G. E. (2017). Neural message passing for quantum chemistry. In D. Precup and Y. W. Teh, editors, Proceedings of the 34th international conference on machine learning,Vol. 70, pages 1263–1272. PMLR.

Gori, M., Monfardini, G., and Scarselli, F. (2005). A new model for learning in graph domains. In Proceedings. 2005 IEEE international joint conference on neural networks, 2005.,Vol. 2, pages 729–734 vol. 2.

Hamilton, W., Ying, Z., and Leskovec, J. (2017). Inductive representation learning on large graphs. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in neural information processing systems,Vol. 30. Curran Associates, Inc.

Kipf, T. N., and Welling, M. (2017). Semi-supervised classification with graph convolutional networks. In International conference on learning representations.

Liu, Q., Nickel, M., and Kiela, D. (2019). Hyperbolic graph neural networks. In H. Wallach, H. Larochelle, A. Beygelzimer, F. dAlché-Buc, E. Fox, and R. Garnett, editors, Advances in neural information processing systems,Vol. 32. Curran Associates, Inc.

Masci, J., Boscaini, D., Bronstein, M. M., and Vandergheynst, P. (2015). Geodesic convolutional neural networks on riemannian manifolds. In 2015 IEEE international conference on computer vision workshop (ICCVW), pages 832–840.

Monti, F., Boscaini, D., Masci, J., Rodolà, E., Svoboda, J., and Bronstein, M. M. (2017). Geometric deep learning on graphs and manifolds using mixture model CNNs. In 2017 IEEE conference on computer vision and pattern recognition (CVPR), pages 5425–5434.

Sanchez-Lengeling, B., Reif, E., Pearce, A., and Wiltschko, A. B. (2021). A gentle introduction to graph neural networks. Distill.

Scarselli, F., Gori, M., Tsoi, A. C., Hagenbuchner, M., and Monfardini, G. (2009). The graph neural network model. IEEE Transactions on Neural Networks, 20(1), 61–80.

Veličković, P., Cucurull, G., Casanova, A., Romero, A., Liò, P., and Bengio, Y. (2018). Graph attention networks. In International conference on learning representations.