トランスフォーマー
深層生成モデル１
2024-02-20
関連ページ
No matching items
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1 歴史
深層学習とは，多層パーセプトロンを用いた機械学習の手法をいう．
1.1 ニューラルネットワークの黎明
1.1.1 脳の解明
(McCulloch and Pitts, 1943) は脳の神経回路を命題論理の枠組みで扱い，ニューロンの論理素子としての機能を考察した（McCulloch-Pitts の形式ニューロンや閾素子と呼ばれる）．なお，パーセプトロンはシグモイド関数を活性化関数に用いた場合，Turing 完全である (Siegelmann and Sontag, 1991)．
脳を模したモデルとして，当然学習能力をどうモデルに組み込むかが問題になる．これはシナプスの結合荷重の変化によるものだという仮設は古くからあったが，最も明確な形で表現したのが (Hebb, 1949) であった．
具体的には Hebb 則は，２つの正の相関を持つ（＝共起しやすい）ニューロンの間の荷重は増強される，というものである．1 これは連想記憶のモデルとして提案された（第 2.7.1 節も参照）．
1.1.2 パーセプトロン
パーセプトロンは，脳の記憶と認識のモデルとして，(Rosenblatt, 1958) が心理学の学会誌に発表した．2
複雑過ぎるものに対する理論解析は進まなかった．
そのような中で (Minsky and Papert, 1969) は線型分離不可能な問題に対しては線型単純パーセプトロンは解を見つけられないほど機能は劣り，かといって複雑なものは計算量が爆発するので，結局パーセプトロンは使い物にならないのではないかとの見方を示した (甘利俊一, 1989, p. 130)．
現状の深層学習の成功を見ている者からすれば，これだけのことでパーセプトロンの研究が下火になってしまったことは驚くべきことに感じる．
(甘利俊一, 1989) はこの点を，次のように断罪している．
ミンスキーらは，自分たちの立てた問題は正しく解いた．しかし問題の立て方を誤ったのである．(甘利俊一, 1989, p. 132)
1.1.3 多層パーセプトロン
パーセプトロンの発明の時点で，深層学習のモデルとしてはすでに完成していた．ただ，(Minsky and Papert, 1969) の指摘の通り，計算複雑性や学習アルゴリズムの問題が残り続けた．
多層のパーセプトロンでは中間層を学習させることが課題であった．これに対しては，活性化関数に可微分なものを用いて確率的勾配降下法によって学習させることで解決できること (Amari, 1967) などは早い時期から議論されていた．この問題点は，局所解に囚われることであった．
多層のパーセプトロンに対して，局所解に囚われるなどの問題はあれど，極めて多くの場合で誤差逆伝播法が有効な学習法になることが広く周知されたのは，(Rumelhart et al., 1986), (Rumelhart et al., 1987) であり，これが深層学習の第二次ブームの着火剤となった．3
すぐさま英語の発音を学習させた研究 (Sejnowski and Rosenberg, 1987) の デモ も発表され，大きな波紋を呼び起こした．ここでも特徴的な内部表現が観察された．
局所解に囚われることが解決された訳ではない．技術的な問題点（特に，結局深層モデルの訓練はうまくいかないこと）はあれど，ニューラルネットワークは実用的に極めて簡単に使えるモデルであると知らしめたのである．
In short, we believe that we have answered Minsky and Papert’s challenge and have found a learning result sufficiently powerful to demonstrate that their pessimism about learning in multilayer machines was misplaced. (Rumelhart et al., 1987, p. 361)
現在は，ドロップアウト や区分的線型な活性化関数 ReLU を用いるなどの工夫がなされている (Goodfellow et al., 2014)．
1.2 深層化の歴史4
1.2.1 深層化の障壁
誤差逆伝播法をニューラルネットに使うことで，表現学習がなされることの発見 (Rumelhart et al., 1986) から，深層学習の分野は次の点で変化したという：
- 神経科学・生物学的なモチベーションから遊離し，より確率論的・統計学的なアプローチが主流になった (Bishop and Bishop, 2024, p. 19)．
- 多層のニューラルネットワークと高次元データに対する理論的な研究が加速した (MacKay, 2003, p. 535)．
しかし，画像識別タスクに特化して結合構造を予め作り込むことで学習を容易にしてある畳み込みニューラルネットワーク (CNN) (LeCun et al., 1998) などを除いて，２層以上のニューラルネットワークの成功した応用例は殆どなかった．これは，勾配消失 により，どんなに多層なニューラルネットワークを構築しても，最後の２層程度しか意味のあるパラメータを学習できなかったためである．
そのために，多層のニューラルネットワークでは表現学習は難しいという認識が広まり，複雑なタスクに対しては，問題固有の特徴抽出技法が編み出されるのみで，一般的な解決法はなかった．
３層のニューラルネットワークも，隠れ層の幅が無限大の極限で，任意の連続関数を近似できるという普遍近似定理という抽象的な慰め (Hecht-Nielsen, 1989) があるのみであった．
そこで多くの研究者は，SVM (Cortes and Vapnik, 1995) やカーネル法，Gauss 過程に現実的な打開策を求め始めたのである．これは冬の時代とも呼ばれる．
1.2.2 ネオコグニトロンと CNN
(Wiesel and Hubel, 1959) は猫の視覚野には，単純細胞と複雑細胞の２種類の細胞があることを発見した．また，生後すぐの猫を一日交代で異なる片目を覆って成長した猫では，多くの視覚野の神経細胞は単眼性になる (Hubel, 1967)．
これらの観察から，(von der Malsburg, 1973) や (Fukushima, 1975) は，特徴抽出細胞が自己形成するメカニズムを，自己組織化のキーワードの下で調べた．特に後者は コグニトロン というモデルを提案した．
(Fukushima, 1980) の ネオコグニトロン は初の深層モデルの例と言える．5 これは，単純細胞層と複雑細胞層を交互に深く重ねたネットワークである．
しかし 福島 は学習の問題を中心に扱った訳ではなかった．6 (LeCun et al., 1998) の畳み込みニューラルネットワーク LeNet は，ネオコグニトロンを誤差逆伝播法により教師あり学習させたものと言える．
このモデルは後に AlexNet としてダントツの性能で世界を驚かせることになる．
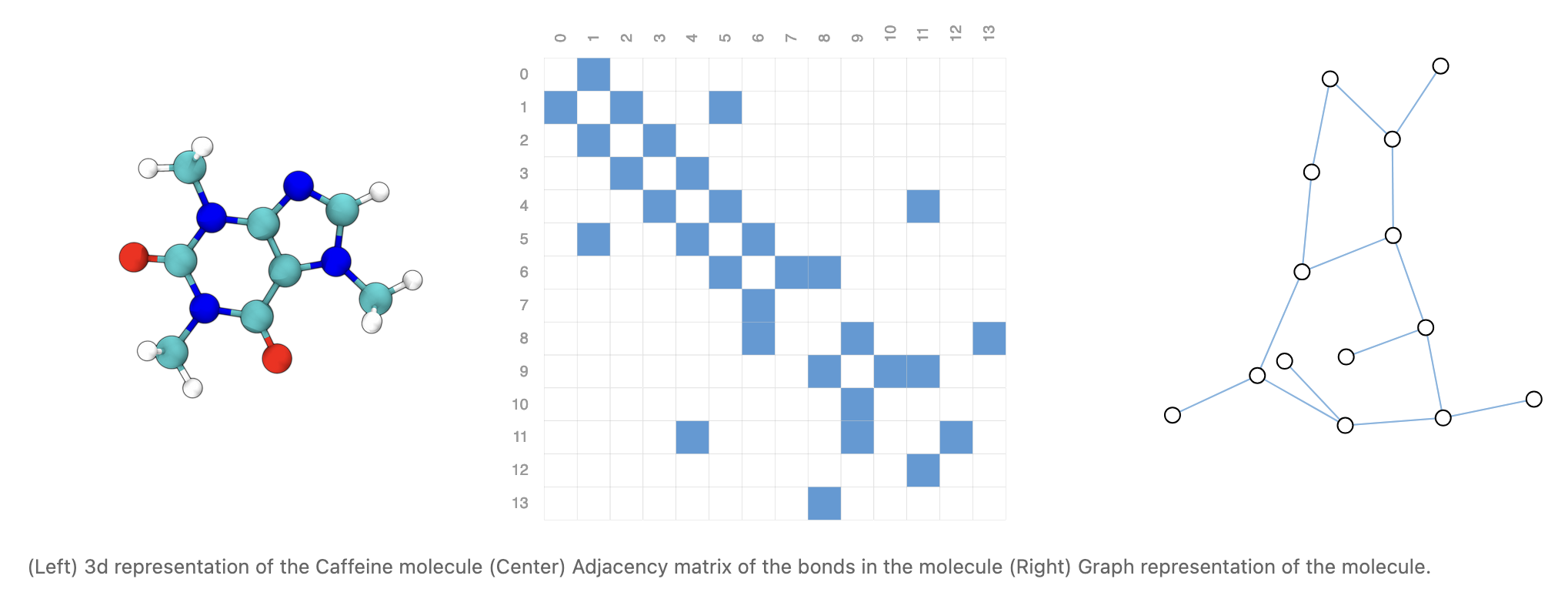
画像データはピクセルを節としたグラフデータとみなすこともでき，CNN を一般化する形で GNN (Graph Neural Network) も提案されている (J. Zhou et al., 2020), (Wu et al., 2021), (Veličković, 2023)．
1.2.3 自己符号化器
(Cottrell and Munro, 1988) は中間層の幅を小さくし，入力信号自身を教師信号として誤差逆伝播法により学習することで，隠れ層に入力の低次元表現が学習され，主成分分析に用いることが出来ることを報告した．
これは入力層と出力層の素子数を一致させ，出力が入力に近づくように訓練される．このようなモデルを 自己符号化器 (autoencoder) または 自己連想ネットワーク (auto-associative neural network) と呼ぶ．
内部表現を獲得するとされる中間層に対して，それより前半の層全体を符号化器，それ以降を復号化器と呼ぶ．7
(Baldi and Hornik, 1989) は活性化関数がない３層の場合，自己符号化器を訓練させることは主成分分析を実行することに等価であることを示した．
さらに層を増やすことで，非線型な次元圧縮が可能であることが (DeMers and Cottrell, 1992) で示された．この論文では，データの空間内の（非線型な）部分多様体の局所座標が学習されたり，人間の顔の写真のデータ圧縮が出来ることが実証されている．
自己符号化器はスタッキングが可能である (Ballard, 1987)．このことが，次の節で述べる事前学習のアイデアに繋がる．
1.2.4 自己符号化器を用いた事前学習 (Bengio et al., 2006)
自己符号化器自体を符号圧縮と表現学習に用いることは，他の手法と比べて特別優れているという訳でもなかった．
しかし，深層ニューラルネットワークを 層ごとに事前に教師なし学習をする ことで，後の教師あり学習において勾配消失などの問題が回避できるというアイデア (Hinton and Salakhutdinov, 2006), (Hinton et al., 2006) は画期的であり，深層学習 (Deep Learning) という言葉が広まったのもこの頃であるという (Schmidhuber, 2015, p. 96)．8
入力に近い方から，１層ごとに，前層の出力を入力として自己符号化器と見て訓練するのである (Bengio et al., 2006)．(Larochelle et al., 2007) はこの事前学習によって，素性の良い局所解の近くにパラメータの初期値が調整されるということを実験的に示している．
この発見は深層模型の訓練を可能にするという大きなブレイクスルーを，教師なしの表現学習と教師あり学習による調整とに問題を分離して解くことによって成し遂げたと言える．
また，単純な自己符号化器の代わりに，ノイズが加えられたデータを入力しこれを復元するようにに学習する denoising autoencoder を用いた方が，深層モデルにより良い初期値を与える潜在表現を獲得できることが報告されている (Vincent et al., 2008)．9
1.2.5 AlexNet (Krizhevsky et al., 2012)
ImageNet データベース (Deng et al., 2009) を用いた判別コンテスト ILSVRC (the ImageNet Large Scale Visual Recognition Challenge) で，ダントツで優勝した AlexNet (Krizhevsky et al., 2012) が大きなターニングポイントとなった．
これも (LeCun et al., 1998) の CNN を基にした８層のモデルで，活性化関数には ReLU とドロップアウトによる正則化が用いられていた．学習も，NVIDIA 社の GPU を用いていた．
1.2.6 ResNet (He et al., 2016)
20 層以上の多層ニューラルネットワークの学習の困難さを初めて解決したのが (He et al., 2016) の Residual Network (ResNet) であった．10
このモデルは 152 層もあったが効率的に訓練することが可能で，2015 年の ILSVRC でダントツで優勝し，しかも初めて人間の誤答率 5% (Dodge and Karam, 2017) を下回ったのである．
そのアイデアは，各層の入力 \(x\) を出力に再度加算した形 \[ y=x+F(x) \] で各層をデザインし，現状の入力からの差分 \(F\) のみを学習するとすることで勾配消失を回避する，というものであった．実際，この層の微分は \[ \frac{d y}{d x}=1+F'(x) \] と表せる．
このテクニックは トランスフォーマー (Vaswani et al., 2017) などのモデルでも用いられている．
(Li et al., 2018) によると，残差レイヤーの追加は誤差関数を滑らかにし，近しい入力に対しても勾配が非常に大きくなってしまうことが効率的な学習を阻害してしまう問題 (shattered gradient problem) (Balduzzi et al., 2017) を解決している，という．
2 アーキテクチャ
2.1 はじめに
ニューラルネットワークは，内部に循環を持つかどうかで二分され，それぞれを Feedforward Network (FFN) と Feedback Network (FBN) と呼ぶ．11
FFN は 多層パーセプトロン (MLP) ともいう．12
Recurrent Neural Network (RNN) 2.4 や Hopfield ネットワーク 2.7.1 は FBN の例である．
多層パーセプトロンは分類や回帰などの統計学的な用途に主に用いられるが，FBN は学習機械として以外に，生物の神経機能のモデルとしてや，組合せ最適化ソルバーとしても用いられる．13
2.2 CNN：畳み込みニューラルネットワーク
CNN はその畳み込み層に特徴付けられる画像に特化した FNN アーキテクチャである．
第 4 節で詳しく扱う．
2.3 AE：自己符号化器
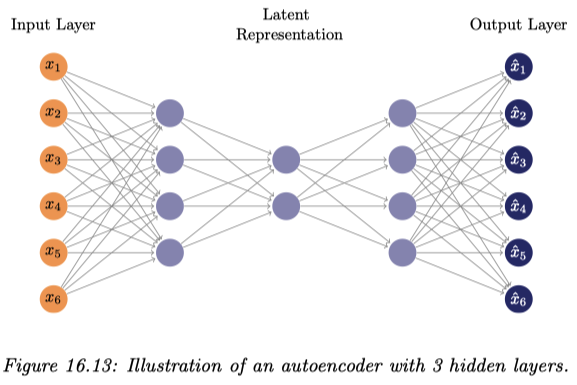
自己符号化器または自己連想ニューラルネットワーク (auto-associative neural network) 1.2.3 は図のような砂時計型の，入力 \(x\) と出力 \(y\) の次元数が一致したアーキテクチャを持ち， \[ \mathcal{L}(\theta)=\|y-x\|^2_2 \] などの入力の復元誤差を目的関数として訓練される．
2.4 RNN：再帰的ニューラルネットワーク
再帰的な層を持ち，自己回帰モデル 3 を実装する FBN の例である．
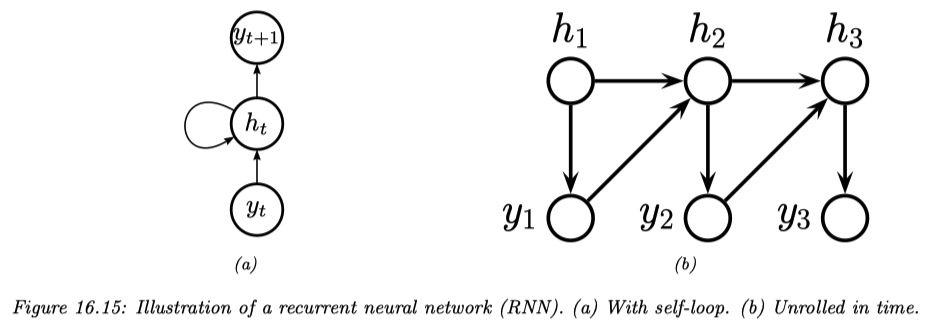
第 3.2 節でも詳しく扱う．
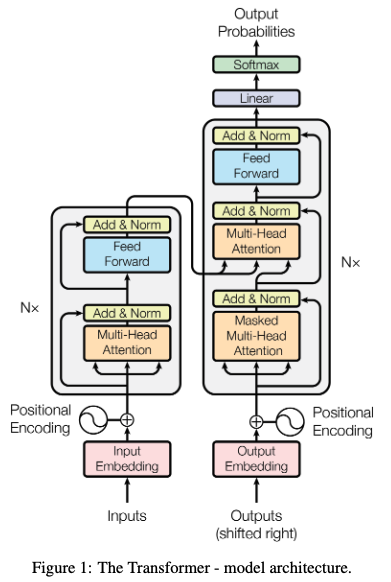
2.5 Transformer
RNN の最大の難点は，隠れ次元 \(z_t\) が \(x_{1:t}\) までの入力の要約になっており，\(x_1\) などの最初の方の情報がどんどん薄れていく点にある．
そこで，時点 \(t\) でも \(x_1\) など以前の情報にワンステップでアクセスできるような機構である 注意機構 が考案された．これがエンコーダーのみのトランスフォーマーである．
デコーダーのみのトランスフォーマーは masked attenstion という技術を用いて \(x_{1:t-1}\) のみで条件づけて \(x_t\) を生成することができる．
一方で，入力全体で条件づけて，文章を生成することもでき，これが最初に (Vaswani et al., 2017) によって提案された，最も一般的な形の encoder-decoder トランスフォーマーである．
No matching items
2.6 GNN：グラフニューラルネットワーク
従来の NN は辺の存在しない退化したグラフに対するものだとして，NN を一般のグラフデータに対して拡張することが近年考えられている．
No matching items
2.7 非有向ネットワーク
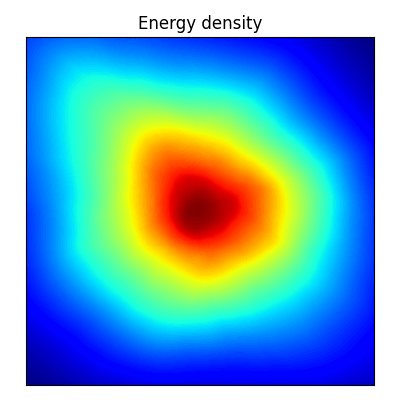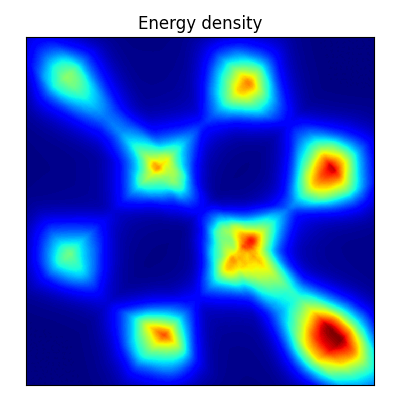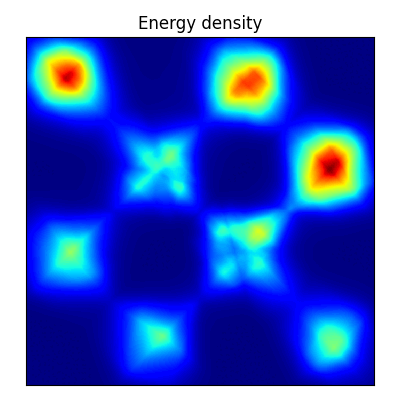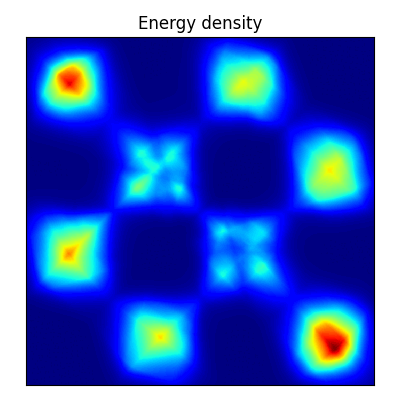
無向グラフが定めるニューラルネットワークは，エネルギーベースモデル (EBM: Energy-Based Model) で主に用いられる．
2.7.1 Hopfield ネットワークとスピングラス
計算機の記憶と生物の記憶の相違点のうち，大きなものには連想性 (associativity) がある．アドレスで整理されているのではなく，内容で整理されているのである．1970 年代には，神経の連想記憶機能のモデルとしてのニューラルネットワークが多数提案された．
それには，ここまで議論してきた階層型のネットワークと異なり，ノード同士は 相互結合 しているものも含まれる．連想記憶のモデルとしては，特に相互結合で，どちらの方向に関する重みも同じであるもの（対称結合 ネットワーク）が多く，全結合の FBN である Hopfield network はその代表例である．14
（連続変数の）Hopfield network の学習則は，Hebb 則 (Hebb, 1949) に基づいて，各ニューロン \(x_j\in[0,1]\) についてその入力 \[ a_i:=\sum_{j}w_{ij}x_j \] を計算し，\(x_i\gets\tanh(a_i)\) と更新する．
実はこの学習則は必ず収束する．このことを，(Hopfield, 1982) はスピングラスのモデルと関連付けて示したことから，特に統計物理学の文脈で Hopfield network の名前がついた．15
神経回路網の解析，とくに連想記憶モデルの解析が，スピングラスを解析する方法を用いて実行できるのではないかという考えが出てきて，大量の物理学者が神経回路網に注目しだした．こうしたアイデアの火付け役がホップフィールドと言われる．(甘利俊一, 1989, p. 105)
対称結合のニューラルネットワークの学習則は，スピングラスと同様に，必ずポテンシャル関数が減少する方に動作するというのである．この連関を利用して，(Hopfield and Tank, 1985) は Hopfield ネットワークをアナログ回路に実装し，巡回セールスマン問題を解くという，最適化問題ソルバーとして利用してみせた．
単体 Hopfield Network (Burns and Fukai, 2023) という拡張もあり，パラメータ数は変わらずとも記憶容量が増える．
2.7.2 ボルツマンマシン (Ackley et al., 1985)
ボルツマンマシンは確率的 Hopfield ネットワークともいい，Hopfield ネットワークが統計物理のモデルとして近似するところの Gibbs 分布を，実際に持つ Markov 確率場 の一種である．16
これは，荷重を，確率 \(\frac{1}{1+e^{-2a_i}}\) で \(x_i=1\)，そうでない場合は \(x_i=-1\) と定めることで得られる．
2.7.3 深層ボルツマンマシン (Salakhutdinov and Hinton, 2009)
2.7.4 深層信念ネットワーク (Hinton et al., 2006)
これは深層学習研究の皮切りになった確率的深層モデルである．
2.8 Spiking Neural Network
実際の神経細胞は 発火 という離散的なイベントを発生させ，その頻度やタイミングも大きな役割を持っている．これを取り入れたモデルを Spiking Neural Network (SNN) (Maass, 1997) と呼ぶ (岡島義憲, 2020)．
SNN は現状の人工ニューラルネット (ANN: Artificial Neural Network) よりも，半導体上での計算を効率化することが出来る．そこで，SNN による深層学習が近年試みられている (Tavanaei et al., 2019)．
Microsoft の BitNet (Wang et al., 2023) も計算効率性を目指すにあたってそのアイデアを等しくする．
2.9 ベイズからの見方
2.9.1 ネットワークの正則化と汎化性能
良い汎化性能を得るためには，偏倚と分散のトレードオフ を乗り越える必要がある．
データセットに対してモデルの自由度が高すぎると，分散は小さくなれど，過学習を起こしてしまう．すなわち，大きなバイアスが導入され，汎化性能が悪くなる．一方で，モデルの自由度が低すぎると，平均的には正しい予測ができても，分散が大きくて役に立たない．
大規模なデータセットを用いることは一つの解決である．自由度の高いモデルを用いても過学習が起こりにくくなるためである．17
2.9.2 帰納バイアス
正則化とは，モデルの自由度を制限することで過学習を抑制することである．これは，「正しいモデルは十分に滑らかであるはずである」という帰納バイアスを導入することで，モデルの汎化性能を改善させていることに等しい．18
転移学習も一種の帰納バイアスの注入だと見れる．２つの異なるタスクの間に類似性が存在するという事前知識を注入することで，汎化性能を改善する手法だと思えるのである．
汎化性能の高いモデルを作るということは，人類が解きたいタスクに普遍的に共通する特徴を捉え，これを帰納バイアスの形でモデルに注入することに等しい．No free lunch theorem (Wolpert, 1996) から，19 一般に特定のタスクに対する性能向上は，他のタスクに対する性能低下を伴うものであることが予想されるが，例えば推定関数が十分滑らかであるというのは，人間の認識特性上，有意義な結果にはほとんど普遍的に必要な条件である．
2.9.3 ベイズ深層学習の美点
(Gal and Ghahramani, 2016) などでは，
- データの数が少なくとも，有効なパラメータ推定が可能である．
- 過学習が起こりにくい．
- 不確実性の定量化が自動でなされる．
と説明される．
2.9.4 ベイズ深層学習の例
CNN は特に過学習しやすい上にサンプル効率性が悪い．その場合には，変分近似による Bayesian CNN は既存法と同等の性能を誇る (Gal and Ghahramani, 2016)．
3 自己回帰モデル
3.1 はじめに
長さ \(T\) のデータベクトルをモデリングするとき， \[ p(x_{1:T})=\prod_{t=1}^Tp(x_t|x_{1:t-1}) \] という分解を用いることができる．このようなアプローチを機械学習では 自己回帰モデル という．20
3.2 RNN
しかし，このようなモデリング法は \(T\) が大きくなるにつれて，条件づける変数 \(x_{1:t-1}\) が高次元になるため，モデリングが難しくなる．
かと言って，\(\{x_t\}_{t=1}^T\) を Markov 連鎖とみなしてモデリングするわけにもいかない．
一つの解決法が 状態空間モデル / 隠れ Markov モデル によるものである．\(x_{1:t}\) はある状態変数 \(z_t\) にある既知の確率法則で圧縮できると仮定し，これのみを持ち越す方法である．
特に，\(X_{1:t-1}\to Z_t\) の対応が決定論的であるとき，これを多層パーセプトロンによってモデリングしたものを 再帰ニューラルネットワーク という．
\(x_t=f(z_{t-1},x_{t-1})\) の関係を学習した後は，\(x_1\) から再帰的に \(f\) に通すことでデータ \(x_{1:T}\) を生成する．
3.3 機械学習の中で占める役割
AR モデルは尤度を効率的に扱えるため，計算や最適化が簡単である．実際，RNN や CNN などの自己回帰モデルが，歴史上最初に発達したアーキテクチャである．
一方で，データの生成が逐次的であるために生成が遅いことや，内部で潜在表現を学習するということがないために表現学習に使うことができない点が欠点と言える．21
4 CNN
CNN はトランスフォーマーによりデータ間の関係を自動的に学習する枠組みが提案される前に，主に画像分野において，データの構造に関する事前知識をモデルに組み込んだ例として提案されたものである．
世界初の深層学習モデルによる席巻は，CNN により，画像認識の分野において達成された．
4.1 Computer Vision という分野
Computer Vision という問題の複雑性が，ニューラルネットワークのアーキテクチャの開発を後押しした歴史がある．
並行移動・拡大変換という2つの合同変換不変性に対して，画像の認識結果は不変であるべきである．
このような不変性，または 同変性 (equivariance) をモデルに取り入れる方法は大きく分けて４つある：
- 誤差関数に正則化項を導入する22
- 対称性を取り入れた潜在表現 を用いてその上で学習をする
- 不変性を効率良く学習出来るように データセットを拡張する
- 対称性を取り扱う構造をネットワークのアーキテクチャに組み込む
CNN は４番目のアプローチで歴史上最初に取られたものである．しかし，このどのアプローチも完全には不変性を取り入れることは出来ていないことも報告されている (Azulay and Weiss, 2019)．
幾何学を種々の変換に対する不変性の研究と捉え直した Felix Klein の Erlangen program に倣い，種々の深層モデルの帰納バイアスとアーキテクチャを，幾何学的な変換から導出してシステマティックに理解する試み Geometric Deep Learning (Bronstein et al., 2021) がある（第 4.6 節）．
4.2 物体認識 CNN
CNN は画像の特徴を，階層的に学習出来るように誘導するような構造を持っている．
多くの例では，畳み込み層とプーリング層が交互に繰り返され，最後に全結合層を持つような構造を持っている．
4.2.1 局所的な特徴
最初の素子は，画像の局所的な一部のみを入力として取る．その範囲を 受容野 (receptive field) と呼ぶ．この素子の荷重を フィルター または カーネル という．
決まったカーネルに対して，この素子はカーネルの特徴にマッチした入力に対して，大きな出力を返す．
次に，このフィルターを畳み込むことで，画像内の異なる位置に存在する特徴を検出する．畳み込み層は，荷重を共有した疎結合層ということになる．
畳み込みを行うと，入力次元と出力次元が変わってしまうことがあるため，その場合は入力画像にパディングを施す．
出力次元を小さくして，畳み込み特徴写像で大きな次元削減を行いたい場合，strided convolution を用いる．
4.2.2 並行移動不変性
畳み込みの結果が，特徴の位置の変化に対して不変になるようにする設計に，プーリング層 または ダウンサンプリング層 (down-sampling / sub-sampling) がある．
プーリングも，受容野を持った素子と畳み込みからなるが，畳み込みに学習されるべきパラメータはなく，確定的な関数と畳み込まれる．
代表的なプーリング関数には 最大プーリング (Y. Zhou and Chellappa, 1988) や平均プーリング，\(l^2\)-プーリングなどがある．
プーリングは不変性の導入に加えて，畳み込み特徴のダウンサンプリングを行って，更なる次元削減を行う役割も果たす．
4.3 画像分割 CNN
画像分類では，１枚の画像に対して１つのクラスの対応づけたが，１つのピクセルに１つのクラスを対応づけることで，画像をクラスごとに分類することが考えられる．
4.3.1 Up-sampling
画像分類の問題では，最終的に全ピクセルから得た情報を１次元に圧縮することになる．一方で，十分な潜在表現を得たのちは up-sampling に転じる Encoder-Decoder 構造にすることで，最終的に元の画像サイズに戻しながら，画像分割問題を解くことが出来る (Long et al., 2015), (Noh et al., 2015), (Badrinarayanan et al., 2017)．
(Badrinarayanan et al., 2017) は max-unpooling などの up-sampling 層の設計を考慮したが，これに学習可能なパラメータを増やした transpose convolution / deconvolution も提案された．
Pooling 層を一切用いず，down-sampling も up-sampling も畳み込み層のみによって行われる場合，これを 全畳み込みネットワーク (fully convolutional network) という (Long et al., 2015)．
4.3.2 U-Net
この encoder-decoder 構造は，分類に必要のない情報を自動的に削減し，モデルのサイズを小さくするのには効果的であるが，タスクによっては元の画像の情報量を保ちたい場合がある．
U-net (Ronneberger et al., 2015) は対応する down-sampling 層と up-sampling 層とを直接繋ぐ経路を追加することでこれを解決した．
4.3.3 Capsule Networks
プーリング層は並行移動不変性の概念を取り入れるが，回転や拡大などの変換に対する不変性を取り入れるにはデータ拡張に依るしかないのでは，CNN の学習はどうしても大規模なデータセットが必要になってしまう．
そこで，アーキテクチャによる解決を試みたのが，畳み込み層に加えて カプセル層 を取り入れた Capsule Network (Sabour et al., 2017) である．
4.4 Inpainting
4.5 スタイル転移
CNN において，最初の方のレイヤーは局所的な特徴を捉えているが，後の方のレイヤーはスタイルなどの大域的な特徴を捉えている．
これを用いて，既存の画像の具体的な特徴を変えずに，他の画像からスタイルのみを転移する手法 Neural Style Transfer が提案された (Gatys et al., 2015), (Gatys et al., 2016)．
4.6 幾何学的深層学習
以上，種々のタスクに種々のアーキテクチャが存在することを見てきた．この状況は，19 世紀の幾何学と似ていると (Bronstein et al., 2021) はいう．
これらのアーキテクチャがどのような帰納バイアスを導入する役割を果たしているかを，不変性や同変性といった第一原理から理解する試みが 幾何学的深層学習 である．
In this text, we make a modest attempt to apply the Erlangen Programme mindset to the domain of deep learning, with the ultimate goal of obtaining a systematisation of this field and ‘connecting the dots’. We call this geometrisation attempt ‘Geometric Deep Learning’, and true to the spirit of Felix Klein, propose to derive different inductive biases and network architectures implementing them from first principles of symmetry and invariance. (Bronstein et al., 2021, p. 2)
化学・生物・物理はいずれも対象の対称性をしっかり扱う理論を持っている．これらの分野に深層学習が広く取り入れられつつある今，深層学習の分野も対称性を第一原理として整理される脱皮が待たれているのである．
4.6.1 幾何学と解析学は双対である
Mikhael Gromov によると，空間 \(X\) の解析学とは \(X\) 上の関数の研究で，\(X\) の幾何学とは \(X\) への関数の研究である (深谷賢治, 1997, p. 11)．
同変性と共変性は，データ集合 \(X\) と群作用 \(\rho:G\times X\to X\) との組 \((X,\rho)\) を取り扱うから，確かに上述の定義に適っている．
4.6.2 20 世紀の数学の方向
4.6.3 共変性と同変性
物体認識 Section 4.2 は不変的で，画像分割 Section 4.3 は同変的な問題である．
ただし，不変性は，\(G\) の \(Y\) への作用が自明である場合の同変性と見れるため，同変性の方が一般的な概念であることに注意．
4.6.4 G-CNN (T. Cohen and Welling, 2016)
一般の群変換に対して，これを帰納バイアスとして取り入れる CNN である Group CNN (T. Cohen and Welling, 2016) が提案されており，医療画像解析での応用 (Lafarge et al., 2021) もなされている．
4.6.5 Steerable CNN (T. S. Cohen and Welling, 2017)
Steerable CNN ではチャンネルの間での対称性を取り入れることができる．
(Weiler et al., 2018) により最先端の性能が発揮されている．
5 終わりに
もはやニューラルネットワークは，layered differentiable model (Oord et al., 2019) と呼んだ方がその数学的な存在をよく表すだろうと思う．
References
Ackley, D. H., Hinton, G. E., and Sejnowski, T. J. (1985). A learning algorithm for boltzmann machines. Cognitive Science, 9(1), 147–169.
Amari, S. (1967). A theory of adaptive pattern classifiers. IEEE Transactions on Electronic Computers, EC-16(3), 299–307.
Azulay, A., and Weiss, Y. (2019). Why do deep convolutional networks generalize so poorly to small image transformations? Journal of Machine Learning Research, 20(184), 1–25.
Badrinarayanan, V., Kendall, A., and Cipolla, R. (2017). SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39(12), 2481–2495.
Baldi, P., and Hornik, K. (1989). Neural networks and principal component analysis: Learning from examples without local minima. Neural Networks, 2(1), 53–58.
Balduzzi, D., Frean, M., Leary, L., Lewis, J. P., Ma, K. W.-D., and McWilliams, B. (2017). The shattered gradients problem: If resnets are the answer, then what is the question? In D. Precup and Y. W. Teh, editors, Proceedings of the 34th international conference on machine learning,Vol. 70, pages 342–350. PMLR.
Ballard, D. H. (1987). Modular learning in neural networks. Proceedings of the Sixth National Conference on Artificial Intelligence, 1, 279–284.
Bengio, Y., Lamblin, P., Popovici, D., and Larochelle, H. (2006). Greedy layer-wise training of deep networks. In Advances in neural information processing systems,Vol. 19, pages 153–160.
Bishop, C. M., and Bishop, H. (2024). Deep learning: Foundations and concepts. Springer Cham.
Bronstein, M. M., Bruna, J., Cohen, T., and Veličković, P. (2021). Geometric deep learning: Grids, groups, graphs, geodesics, and gauges.
Burns, T. F., and Fukai, T. (2023). Simplicial hopfield networks. In The eleventh international conference on learning representations.
Cohen, T. S., and Welling, M. (2017). Steerable CNNs. In International conference on learning representations.
Cohen, T., and Welling, M. (2016). Group equivariant convolutional networks. In M. F. Balcan and K. Q. Weinberger, editors, Proceedings of the 33rd international conference on machine learning,Vol. 48, pages 2990–2999. New York, New York, USA: PMLR.
Cortes, C., and Vapnik, V. (1995). Support-vector networks. Machine Learning, 20, 273–297.
Cottrell, G. W., and Munro, P. (1988). Principal component analysis of images via back propagation. In Proceedings of SPIE visual communications and image processings,Vol. 1001, pages 1070–1076.
DeMers, D., and Cottrell, G. (1992). Non-linear dimensionality reduction. In Advances in neural information processing systems,Vol. 5, pages 580–587.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei, L. (2009). ImageNet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255.
Dodge, S., and Karam, L. (2017). A study and comparison of human and deep learning recognition performance under visual distortions.
Fukushima, K. (1975). Cognitron: A self-organizing multilayered neural network. Biological Cybernetics, 20, 121–136.
Fukushima, K. (1980). Neural network model for a mechanism of pattern recognition unaffected by shift in position–neocognitron. Biological Cybernetics, 36, 193–202.
Gal, Y., and Ghahramani, Z. (2016). Bayesian convolutional neural networks with bernoulli approximate variational inference. In International conference on learning representations.
Gatys, L. A., Ecker, A. S., and Bethge, M. (2015). A neural algorithm of artistic style.
Gatys, L. A., Ecker, A. S., and Bethge, M. (2016). Image style transfer using convolutional neural networks. In 2016 IEEE conference on computer vision and pattern recognition (CVPR), pages 2414–2423.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., … Bengio, Y. (2014). Generative adversarial nets. In Advances in neural information processing systems,Vol. 27, pages 1–9.
Gromov, M. (2001). Possible trends in mathematics in the coming decades. In B. Engquist and W. Schmid, editors, Mathematics unlimited — 2001 and beyond, pages 525–527. Berlin, Heidelberg: Springer Berlin Heidelberg.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778.
Hebb, D. O. (1949). The organization of behavior: A neuropsychological theory. John Wiley & Sons, Chapman; Hall.
Hecht-Nielsen, R. (1989). Theory of the backpropagation neural network. In International 1989 joint conference on neural networks.
Hinton, G. E., Esindero, S., and Teh, Y.-W. (2006). A fast learning algorithm for deep belief nets. Naural Computation, 18(7), 1527–1554.
Hinton, G. E., and Salakhutdinov, R. R. (2006). Reducing the dimensionality of data with neural networks. Science, 313(5786), 504–507.
Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Science, 79(8), 2554–2558.
Hopfield, J. J., and Tank, D. W. (1985). "Neural" computation of decisions in optimization problems. Biological Cybernetics, 52, 141–152.
Horita, D., Yang, J., Chen, D., Koyama, Y., Aizawa, K., and Sebe, N. (2023). A structure-guided diffusion model for large-hole image completion.
Hubel, D. H. (1967). Effects of distortion of sensory input on the visual system of kittens. The Physiologist, 10, 17–45.
Koller, D., and Friedman, N. (2009). Probabilistic graphical models. MIT Press.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). ImageNet classification with deep convolutional neural networks. In Advances in neural information processing systems,Vol. 25.
Lafarge, M. W., Bekkers, E. J., Pluim, J. P. W., Duits, R., and Veta, M. (2021). Roto-translation equivariant convolutional networks: Application to histopathology image analysis. Medical Image Analysis, 68, 101849.
Larochelle, H., Erhan, D., Courville, A., Bergstra, J., and Bengio, Y. (2007). An empirical evaluation of deep architectures on problems with many factors of variation. In Proceedings of the 24th international conference on machine learning, pages 473–480. New York, NY, USA: Association for Computing Machinery.
LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Li, H., Xu, Z., Taylor, G., Studer, C., and Goldstein, T. (2018). Visualizing the loss landscape of neural nets. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, editors, Advances in neural information processing systems,Vol. 31. Curran Associates, Inc.
Long, J., Shelhamer, E., and Darrell, T. (2015). Fully convolutional networks for semantic segmentation. In 2015 IEEE conference on computer vision and pattern recognition (CVPR), pages 3431–3440. Los Alamitos, CA, USA: IEEE Computer Society.
Maass, W. (1997). Networks of spiking neurons: The third generation of neural network models. Neural Networks, 10(9), 1659–1671.
MacKay, D. J. C. (2003). Information theory, inference and learning algorithms. Cambridge University Press.
McCulloch, W., and Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 7, 115–133.
Minsky, M., and Papert, S. A. (1969). Perceptrons: An introduction to computational geometry. The MIT Press.
Murphy, K. P. (2023). Probabilistic machine learning: Advanced topics. MIT Press.
Noh, H., Hong, S., and Han, B. (2015). Learning deconvolution network for semantic segmentation. In 2015 IEEE international conference on computer vision (ICCV), pages 1520–1528. Los Alamitos, CA, USA: IEEE Computer Society.
Oord, A. van den, Li, Y., and Vinyals, O. (2019). Representation learning with contrastive predictive coding.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. In N. Navab, J. Hornegger, W. M. Wells, and A. F. Frangi, editors, Medical image computing and computer-assisted intervention – MICCAI 2015, pages 234–241. Cham: Springer International Publishing.
Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6), 386–408.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323, 533–536.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1987). Parallel distributed processing: Explorations in the microstructure of cognition: foundations. In D. E. Rumelhart and J. L. McClelland, editors, pages 318–362. MIT Press.
Sabour, S., Frosst, N., and Hinton, G. E. (2017). Dynamic routing between capsules. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, editors, Advances in neural information processing systems,Vol. 30. Curran Associates, Inc.
Salakhutdinov, R., and Hinton, G. (2009). Deep boltzmann machines. In Proceedings of the twelth international conference on artificial intelligence and statistics,Vol. 5, pages 448–455.
Schmidhuber, J. (2015). Deep learning in neural networks: An overview. Neural Networks, 61, 85–117.
Sejnowski, T. J., and Rosenberg, C. R. (1987). Parallel networks that learn to pronounce english text. Complex Systems, 1(1), 145–168.
Shalev-Shwartz, S., and Ben-David, S. (2014). Understanding machine learning: From theory to algorithms. Cambridge University Press.
Siegelmann, H. T., and Sontag, E. D. (1991). Turing computability with neural nets. Applied Mathematics Letters, 4(6), 77–80.
Simard, P., Victorri, B., LeCun, Y., and Denker, J. (1991). Tangent prop - a formalism for specifying selected invariances in an adaptive network. In J. Moody, S. Hanson, and R. P. Lippmann, editors, Advances in neural information processing systems,Vol. 4. Morgan-Kaufmann.
Simonyan, K., and Zisserman, A. (2015). Very deep convolutional networks for large-scale image recognition. In International conference on learning representations,Vol. 3, pages 1–14.
Tavanaei, A., Ghodrati, M., Kheradpisheh, S. R., Masquelier, T., and Maida, A. (2019). Deep learning in spiking neural networks. Neural Networks, 111, 47–63.
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems,Vol. 30.
Veličković, P. (2023). Everything is connected: Graph neural networks. Current Opinion in Structural Biology, 79, 102538.
Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-A. (2008). Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th international conference on machine learning, pages 1096–1103. New York, NY, USA: Association for Computing Machinery.
von der Malsburg, C. (1973). Self-organization of orientation sensitive cells in the striate cortex. Kybernetik, 14, 85–100.
Wang, H., Ma, S., Dong, L., Huang, S., Wang, H., Ma, L., … Wei, F. (2023). BitNet: Scaling 1-bit transformers for large language models. arXiv.
Weiler, M., Hamprecht, F. A., and Storath, M. (2018). Learning steerable filters for rotation equivariant CNNs. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR).
Wiesel, D. H., and Hubel, T. N. (1959). Receptive fields of single neurones in the cat’s striate cortex. Journal of Physiology, 148(3), 574–591.
Wolpert, D. H. (1996). The lack of a priori distinctions between learning algorithms. Neural Computation, 8(7), 1341–130.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Yu, P. S. (2021). A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 32(1), 4–24.
Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C., Liu, Z., … Sun, M. (2020). Graph neural networks: A review of methods and applications. AI Open, 1, 57–81.
Zhou, Y., and Chellappa, R. (1988). Computation of optic flow using a neural network. In IEEE 1988 international conference on neural networks.
岡島義憲. (2020). Spiking neural network 技術の現状と課題に関する考察. 人工知能学会第二種研究会資料, 2020(AGI-015), 08.
深谷賢治. (1997). 「位相的場の理論」 集中講義ノート.
甘利俊一. (1989). 神経回路網モデルとコネクショニズム,Vol. 22. 東京大学出版会.
福水健次. (2024). Machine learning with group theory.
麻生英樹, 安田宗樹, 前田新一, 岡野原大輔, 岡谷貴之, 久保陽太郎, and ボレガラダヌシカ. (2015). 深層学習. 近代科学社.
Footnotes
(MacKay, 2003, p. 506) など．↩︎
入力層と中間層と出力層の３層のみからなるものモデルを単純パーセプトロンと呼ぶが，それだけでなく，多層のものや，フィードバック結合のあるものも含む，一般的な形で考えていた．↩︎
オートエンコーダーを導入し，中間層で表現学習がなされること（最も幅の狭い中間層の活性化を通じてコンパクトに表現する，など）と，モーメンタムが学習を加速することを示している (Rumelhart et al., 1987, p. 330), (Schmidhuber, 2015)．「バックプロパゲーションがこの流行の起爆剤となったとさえ言える」 (甘利俊一, 1989, p. 144)．↩︎
(Schmidhuber, 2015), (Bishop and Bishop, 2024), (麻生英樹 et al., 2015) を参考．↩︎
教師なしの競合学習を試みたのみであった (麻生英樹 et al., 2015, p. 21)．↩︎
三層の場合は，入力層を符号化器，出力層を復号化器とも言う．さらに中間層の幅が小さい場合，その形から hourgalss-type neural network とも呼ばれる (麻生英樹 et al., 2015, p. 91)．↩︎
さらに，Hinton らが示した成功は，深層信念ネットワークは制約付き Boltzmann マシン (RBM) として各層が事前訓練されたが，これが denoising autoencoder と似たノイズへのロバスト性を示すために起こったものではないかと予想している (Vincent et al., 2008) 第６節．↩︎
当時の CNN で深かったものには，19 層の CNN である VGGNet (Simonyan and Zisserman, 2015) がある．↩︎
(MacKay, 2003, p. 505)，(Murphy, 2023, p. 633) 16.3.1節など．↩︎
(Murphy, 2023, p. 632) 16.3.1節など．↩︎
(MacKay, 2003, p. 468) の導入も参照．↩︎
(MacKay, 2003, p. 503) 第42章，(麻生英樹 et al., 2015, p. 11) など．↩︎
「このため，物理学者はこの種のモデルのことを Hopfield モデルと呼ぶが，この命名は適切とは思えない」(甘利俊一, 1989, p. 97) としている．↩︎
“The popularity of the Boltzmann machine was primarily driven by its similarity to an activation model for neurons.” (Koller and Friedman, 2009, p. 126)．↩︎
(Wolpert, 1996) は最適化の文脈での定理を示した．統計的機械学習の文脈での No free lunch theorem は，“Any classifier with finite sample error guarantees necessarily needs inductive bias: structural assumptions on either the function class or the sampling distribution.” と説明できる．(Shalev-Shwartz and Ben-David, 2014, p. 37) 定理5.1 も参照．↩︎
(Murphy, 2023, p. 811) 22章など．↩︎
(Murphy, 2023, p. 812) など．↩︎
tangent propagation (Simard et al., 1991) などがその例である．2の例とも見れる．↩︎
(福水健次, 2024), (Bronstein et al., 2021, pp. 15–16) など．または nLab も参照．↩︎