Lévy 過程を見てみよう

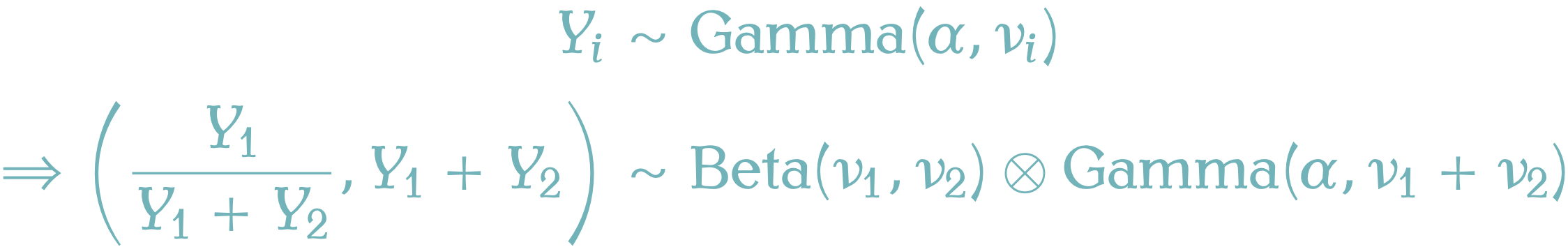
A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

YUIMAについては次の記事も参照：

YUIMA 入門

確率微分方程式のシミュレーションと推測のためのパッケージ`yuima`の構造と使い方をまとめます．

Poisson 過程と複合 Poisson 過程については次の記事を参照：

Poisson 過程を見てみよう

YUIMA パッケージを用いたシミュレーションを通じて

1 Lévy-Itô 分解

1.1 加法過程の定義

定義 (additive process, Lévy process)¹

確率過程 \(\{X_t\}\subset\mathcal{L}(\Omega;\mathbb{R}^d)\) が 加法過程 であるとは，最初の４条件を満たすことをいう．５条件全てを満たすとき，Lévy 過程 であるという．

1. \(X_0\overset{\text{a.s.}}{=}0\)．
2. ある充満集合 \(\Omega_0\subset\Omega\) が存在し，\(t\mapsto X_t(\omega)\) は càdlàg である．
3. 独立増分：任意の \(0\le t_0<\cdots<t_n\) について， \[ X_{t_0},X_{t_1}-X_{t_0},X_{t_2}-X_{t_1},\cdots,X_{t_n}-X_{t_{n-1}} \] は独立である．
4. 確率連続：任意の \(\epsilon>0\) と \(t\ge0\) について， \[ \lim_{s\to t}\operatorname{P}[\lvert X_s-X_t\rvert>\epsilon]=0 \] が成り立つ．
5. 定常増分：\(X_{s+t}-X_s\) の分布は \(s\ge0\) に依らない．

1.2 特性量

加法過程 \(\{X_t\}\) について，\(X_t\) の分布は必ず \(\mathbb{R}^d\) 上の無限可分分布になる．²

加えて，加法過程の分布は１次元の有限次元分布族が特徴付ける．

定理（加法過程の分布）³

\(\{X_t\}\subset\mathcal{L}(\Omega;\mathbb{R}^d)\) を加法過程とする．

1. \(\mu_{s,t}\) を \(X_t-X_s\) の分布とすると，これは無限可分であり，次を満たす： \[ \mu_{s,t}*\mu_{t,u}=\mu_{s,u}, \] \[ \mu_{s,s}=\delta_0, \] \[ \mu_{s,t}\to\delta_0\quad(s\nearrow t), \] \[ \mu_{s,t}\to\delta_0\qquad(t\searrow s). \]
2. 確率分布の族 \(\{\mu_{s,t}\}\subset\mathcal{P}(\mathbb{R}^d)\) が上の４式を満たすならば，これはある加法過程 \(\{X_t\}\) が定める分布である．
3. ２つの加法過程 \(X,X'\) が， \[ X_t\overset{\text{d}}{=}X'_t\quad t\in\mathbb{R}_+ \] を満たすならば，\(X\overset{\text{d}}{=}X'\) が成り立つ．

このことにより，加法過程 \(X\) の分布は，各 \(X_t\) の無限可分分布を特徴付ける特性量 \((A_t,\nu_t,\gamma(t))\) によって特徴付けられる．

無限可分分布の特徴付け (Khinchin and Lévy, 1936)⁴

特性関数 \(f:\mathbb{R}^d\to\mathbb{C}\) について，次は同値：

1. \(f\) は無限可分である．
2. (Lévy) ある \[ \nu(\{0\})=0,\qquad\int_{\mathbb{R}^d}(\lvert x\rvert^2\land1)\nu(dx)<\infty \] を満たす測度 \(\nu\in\mathcal{M}(\mathbb{R}^d)\) と対称な半正定値行列 \(A\in S_n(\mathbb{R})_+\) と \(\gamma\in\mathbb{R}^d\) が一意的に存在して，次のように表せる： \[ f(z)=\exp\left(-\frac{1}{2}(z|Az)+i(\gamma|z)+\int_{\mathbb{R}^d}\biggr(e^{i(z|x)}-1-i(z|x)1_{\left\{B^d\right\}}(x)\biggl)\nu(dx)\right). \]
3. (Khinchin) ある有限測度 \(\Psi\in\mathcal{M}^1(\mathbb{R}^d)\) と \(\alpha\in\mathbb{R}^d\) が存在して，次のように表せる： \[ f(u)=\exp\left(i(\alpha|u)+\int_{\mathbb{R}^d}\biggr(e^{i(u|x)}-1-\frac{i(u|x)}{1+\lvert x\rvert^2}\biggl)\frac{1+\lvert x\rvert^2}{\lvert x\rvert^2}\Psi(dx)\right). \]

\(A\) を Gauss 共分散，\(\nu\) を Lévy 測度，\(\Psi\) を Khintchine測度 という．⁵

加えて，任意の半正定値行列 \(A\)，\(\gamma\in\mathbb{R}^d\)，Lévy 測度 \(\nu\) であって \(\nu(\{0\})=0\) かつ \[ \int_{\mathbb{R}^d}(\lvert x\rvert^2\land1)\nu(dx)<\infty \] を満たすものに対して，\((A,\nu,\gamma)\) を特性量にもつ無限可分分布が存在する．

Khintchin の表示はより直接的である上に，Khintchin 測度は有限になる．さらに，\((\alpha,\Psi)\) の収束が過程の収束にも対応する！⁶ だが，確率論的な意味付けに欠けるために，Lévy の表示の方をここでは用いる．

Lévy の表示の被積分関数 \[ e^{i(z|x)}-1-i(z|x)1_{\left\{B^d\right\}}(x) \] は大変複雑であるが，こうしないと \(\nu\)-可積分にならないのである．

\(\nu\) は \(O(\lvert x\rvert^2)\) 関数に関してならば \(0\) の近傍でも可積分であるから，\(e^{i(z|x)}\) から１次以下の項を \(0\) の近傍から取り去ることで可積分にしているのである．そのため，最後の項は \(1_{\left\{B^d\right\}}\) でなくとも， \[ c(x)=1+o(\lvert x\rvert)\quad(\lvert x\rvert\to0) \] \[ c(x)=O(\lvert x\rvert^{-1})\quad(\lvert x\rvert\to\infty) \] の２条件を満たすものならばなんでも良い．だが，取り替える度に１次の項 \(\gamma\in\mathbb{R}^d\) を変更する必要がある．

一般に \(\gamma\) はドリフトと呼んではいけない． \[ \int_{B^d}\lvert x\rvert\,\nu(dx)<\infty \] を満たす場合のみ， \[ f(z)=\exp\left(-\frac{(z|Az)}{2}+i(\gamma_0|z)+\int_{\mathbb{R}^d}\biggr(e^{i(z|x)}-1\biggl)\nu(dx)\right) \] と表示でき，この際の \(\gamma_0\in\mathbb{R}^d\) を ドリフト と呼ぶ．

逆に， \[ \int_{\mathbb{R}^d\setminus B^d}\lvert x\rvert\,\nu(dx)<\infty \] が成り立つとき， \[ f(z)=\exp\left(-\frac{(z|Az)}{2}+i(\gamma_1|z)+\int_{\mathbb{R}^d}\biggr(e^{i(z|x)}-1-i(z|x)\biggl)\nu(dx)\right) \] と表示でき，\(\gamma_1\) は \(f\) が定める確率分布の平均に一致する．⁷

Lévy 過程は，\(A:=A_1,\nu:=\nu_1,\gamma:=\gamma(1)\) について， \[ A_t=tA,\quad\nu_t=t\nu,\quad\gamma_t=t\gamma \] と表せる場合に当たる．

1.3 強度測度との関係

\(\{(A_t,\nu_t,\gamma_t)\}_{t\in\mathbb{R}_+}\) を加法過程の特性量とする．

このとき， \[ \widetilde{\nu}([0,t]\times B):=\nu_t(B),\qquad t\ge0,B\in\mathcal{B}(\mathbb{R}^d) \] は \(\mathbb{R}_+\times\mathbb{R}^d\) 上に測度を定める．

命題（強度測度と特性測度の関係）⁸

測度の族 \(\{\nu_t\}\subset\mathbb{M}(\mathbb{R}^d)\) と測度 \(\nu\in\mathcal{M}(\mathbb{R}_+\times\mathbb{R}^d)\) について，次は同値：

1. \(\widetilde{\nu}\) は次の２条件を満たす： \[ \widetilde{\nu}(\{t\}\times\mathbb{R}^d)=0, \] \[ \int_{[0,t]\times\mathbb{R}^d}(1\land\lvert x\rvert^2)\widetilde{\nu}(dsdx)<\infty. \]
2. \(\{\nu_t\}\) はある加法過程の特性測度である．

よって，任意の加法過程について， \[ \int_{\mathbb{R}^d}(1\land\lvert x\rvert^2)\nu_t(dx)<\infty \] が必要である．

Lévy 過程であるとき，定常増分であることが必要であるため，跳躍時刻は \(\mathbb{R}_+\) 上の一様な Poisson 点過程に従う必要がある．これより， \[ \widetilde{\nu}=\ell_+\otimes\nu \] と分解できる必要があり，この特性測度 \(\nu\) が Lévy 測度である．このとき，\(\nu_t=t\nu\) かつ \(\widetilde{\nu}(dsdx)=ds\nu(dx)\)．

1.4 一般の分解

定理 (Ito, 1941)⁹

\(\{X_t\}\subset\mathcal{L}(\Omega;\mathbb{R}^d)\) を特性量 \(\{(A_t,\nu_t,\gamma(t))\}\) を持つ加法過程とする． \[ \eta(\omega,B):=\#\left\{t\in\mathbb{R}_+\,\middle|\,\begin{pmatrix}t\\X_t(\omega)-X_{t-}(\omega)\end{pmatrix}\in B\right\} \] を \(\omega\in\Omega_0\) 上で \(B\in\mathcal{B}(\mathbb{R}^+\times\mathbb{R}^d\setminus\{0\})\) に関して定める．

1. \(\eta\) は \(\mathbb{R}^+\times\mathbb{R}^d\setminus\{0\}\) 上の強度測度 \(\widetilde{\nu}\) を持った Poisson 点過程である．
2. ある充満集合 \(\Omega_1\subset\Omega\) が存在して，この上で次が定まる： \[\begin{align*} X^1_t(\omega)&:=\lim_{\epsilon\searrow0}\int_0^t\int_{\left\{\epsilon<\lvert x\rvert\le 1\right\}}x\,\widetilde{\nu}(\omega,dsdx)\\ &\qquad+\int_0^t\int_{\mathbb{R}^d\setminus B^d}x\,\eta(\omega,dsdx) \end{align*}\] 収束は \(t\in\mathbb{R}_+\) に関して広義一様であり，\(X^1\) は特性量 \(\{(0,\nu_t,0)\}_{t\in\mathbb{R}_+}\) が定める加法過程である．
3. \(X^2_t:=X_t-X_t^1\) は殆ど確実に連続な見本道を持ち，特性量 \(\{(A_t,0,\gamma(t))\}\) が定める加法過程である．
4. \(X^1\perp\!\!\!\perp X^2\) が成り立つ．

1.5 B 型の場合

\[ \int_{B^d}\lvert x\rvert\,\nu_t(dx)<\infty,\quad t>0 \] を満たす場合，Poisson 補過程によらない，より簡潔な表示を持つ．

定理

\[ \int_{B^d}\lvert x\rvert\,\nu_t(dx)<\infty,\quad t>0 \] が成り立つ場合，次が成り立つ：

1. ある充満集合 \(\Omega_3\subset\Omega\) が存在して，この上で次が定まる： \[ X^3_t(\omega):=\int_0^t\int_{\mathbb{R}^d\setminus\{0\}}x\,\eta(\omega,dsdx). \] このとき，\(X_t^3\) の分布は複合 Poisson である： \[ \operatorname{E}[e^{i(z|X_t^3)}]=\exp\left(\int_{\mathbb{R}^d}\biggr(e^{i(z|x)}-1\biggl)\nu_t(dx)\right). \]
2. \(X^4_t:=X_t-X_t^3\) は殆ど確実に連続な見本道を持ち，Gauss 過程を定める： \[ \operatorname{E}[e^{i(z|X_t^4)}]=\exp\left(-\frac{1}{2}(z|A_tz)+i(\gamma_0(t)|z)\right). \]
3. \(X^3\perp\!\!\!\perp X^4\) が成り立つ．

2 Lévy 測度

2.1 導入

本節の目的は，Lévy 過程の次の３分類の見本道の違いを理解することである：¹⁰

特性量 \((A,\nu,\gamma)\) を持つ Lévy 過程について，

• A 型：\(A=0\) かつ \(\nu(\mathbb{R}^d)<\infty\)．
• B 型：\(A=0\) かつ \(\int_{B^d}\lvert x\rvert\,\nu(dx)<\infty\) であるが，A 型ではない．
• C 型：それ以外．

• \(A\) 型は拡散項を持たず，確定的な動きと複合 Poisson 過程の和で表現される．ジャンプは離散的に起こる．

• \(B\) 型も拡散項を持たないが，\(\mathbb{R}_+\) 上稠密な可算集合上でジャンプを繰り返す．Gamma 過程（第 3.6 節）がその例である．

• \(A,B\) は殆ど確実に任意の有界区間上で有界変動な見本道を持つが，\(C\) 型は有界変動ではない．¹¹ Brown 運動と Cauchy 過程（第 4.4 節）がその例である．

2.2 Lévy 測度が零ならば，Gauss 過程である

命題（連続な Lévy 過程の特徴付け）¹²

Lévy 過程 \(X\) について，次の２条件は同値：

1. \(X\) は殆ど確実に連続な見本道を持つ．
2. \(\nu=0\) である．

証明

時刻 \(t>0\) までの跳躍回数を表す Poisson 過程 \[ N_t:=\int_0^t\int_{\mathbb{R}^d\setminus\{0\}}\eta(dsdx)\in[0,\infty] \] を考えると， \[ \operatorname{E}[N_t]=\int_0^t\int_{\mathbb{R}^d\setminus\{0\}}ds\nu(dx)=0. \] すなわち，\(N_t=0\;\;\text{a.s.}\)

2.3 区分定数ならば，A 型である．

命題（A 型の見本道の特徴付け）¹³

Lévy 過程 \(X\) ついて，次の３条件は同値：

1. \(X\) の見本道は，殆ど確実に区分的定数であり，有界区間上では有限回のジャンプしか起こらない．
2. \(X\) は複合 Poisson 分布であるか，零であるかのいずれかである．
3. \(X\) は A 型で，かつ \(\gamma_0=0\) である．

証明

• 1 \(\Rightarrow\) 2

  任意の有限区間内でのジャンプ回数は有限回であるため，ジャンプ回数の Poisson 過程 \(N\) について，\(N_t\sim\mathrm{Pois}(t\nu(\mathbb{R}^d))\) の母数は有限である必要がある．特に \(\nu(\mathbb{R}^d)<\infty\)．\(X\) に連続部分がないことを併せると，定理 1.5 より， \[ \operatorname{E}[e^{i(z|X_t)}]=\exp\left(t\int_{\mathbb{R}^d}\biggr(e^{i(z|x)}-1\biggl)\nu(dx)\right). \] これは \(\mathrm{CP}(t,\nu)\) の特性関数である．

• 2 \(\Rightarrow\) 1

  こちらは省略する．

純粋跳躍確率過程であっても，B 型ならば，見本道は区分的定数にはならない．Gamma 過程（第 3.6 節）がその例である．

2.4 B 型の跳躍時刻

Lévy 過程の見本道は右連続であるから，\(\mathbb{R}_+\) 上トータルの跳躍回数は殆ど確実に可算回である．

\(\nu(\mathbb{R}^d)=\infty\) の場合は，有限区間上での跳躍回数も無限になる．

さらに，次のことが言える：

命題（B 型 Lévy 過程のジャンプ時刻）¹⁴

\(\nu(\mathbb{R}^d)=\infty\) とする．このとき，跳躍時刻は殆ど確実に \(\mathbb{R}_+\) 上稠密である．

証明

\(\nu(\mathbb{R}^d)=\infty\) のとき， \[ T_\epsilon(\omega):=\inf\left\{t\ge 0\mid\lvert X_t(\omega)-X_{t-}(\omega)\rvert>\epsilon\right\} \] とすると， \[ \lim_{\epsilon\searrow0}\operatorname{P}[T_\epsilon\le t]=1. \] よって， \[ \lim_{\epsilon\searrow0}T_\epsilon=0\;\;\text{a.s.} \] これは，ある充満集合 \(\Omega_0\subset\Omega\) の上で，\(0\) が \(X\) の跳躍時刻の触点になることを含意している．

これと同様の議論を任意の \(s\in\mathbb{Q}\cap\mathbb{R}_+\) について繰り返すことで，ある充満集合 \[ \bigcap_{s\in\mathbb{Q}\cap\mathbb{R}_+}\Omega_s \] 上で，\(X\) の跳躍時刻の閉包が \(\mathbb{R}_+\) 上で稠密になることがわかる．

2.5 従属過程ならば B 型である

\(d=1\) で，殆ど確実に単調増加な見本道を持つ Lévy 過程を 従属過程 (subordinator) という．¹⁵

命題（単調増加性の特徴付け）¹⁶

\(d=1\) とし，\(X\) を Lévy 過程とする．このとき，次は同値：

1. \(X\) は従属過程である．
2. \(A=0,\nu((-\infty,0))=0\) かつ \[ \int_{[0,1)}x\,\nu(dx)<\infty \] 加えて \(\gamma_0\ge0\) である．

仮に \(A=0,\nu((-\infty,0))=0\) だが， \[ \int_0^1x\,\nu(dx)=\infty \] であったとする．

このとき，正なジャンプとドリフトしか持たないはずであるから，場合によっては単調増加過程になっても良さそうなものである．

しかし，このような過程が発散せずに well-defined であるということは，負の方向に無限に強いドリフトを持っており，これが正なジャンプを打ち消していることが必要である．

それ故，ジャンプの隙間では負方向のドリフトが競り勝ち，全体としては単調増加にならない．特に，任意の区間において単調増加にならない．¹⁷

2.6 C 型ならば非有界変動である

命題（見本道の変動）¹⁸

Levy 過程 \(X\) について，

1. A 型または B 型ならば，有界変動過程である．すなわち，殆ど確実に，任意の \(t>0\) について，\([0,t]\) 上で有界変動である．
2. C 型ならば，殆ど確実に，任意の \(t>0\) について，\([0,t]\) 上で有界変動でない．

3 従属過程と Gamma 過程

3.1 導入

Gamma 過程は，拡散項もドリフト \(\gamma_0\) も持たない，純粋跳躍な従属過程である．

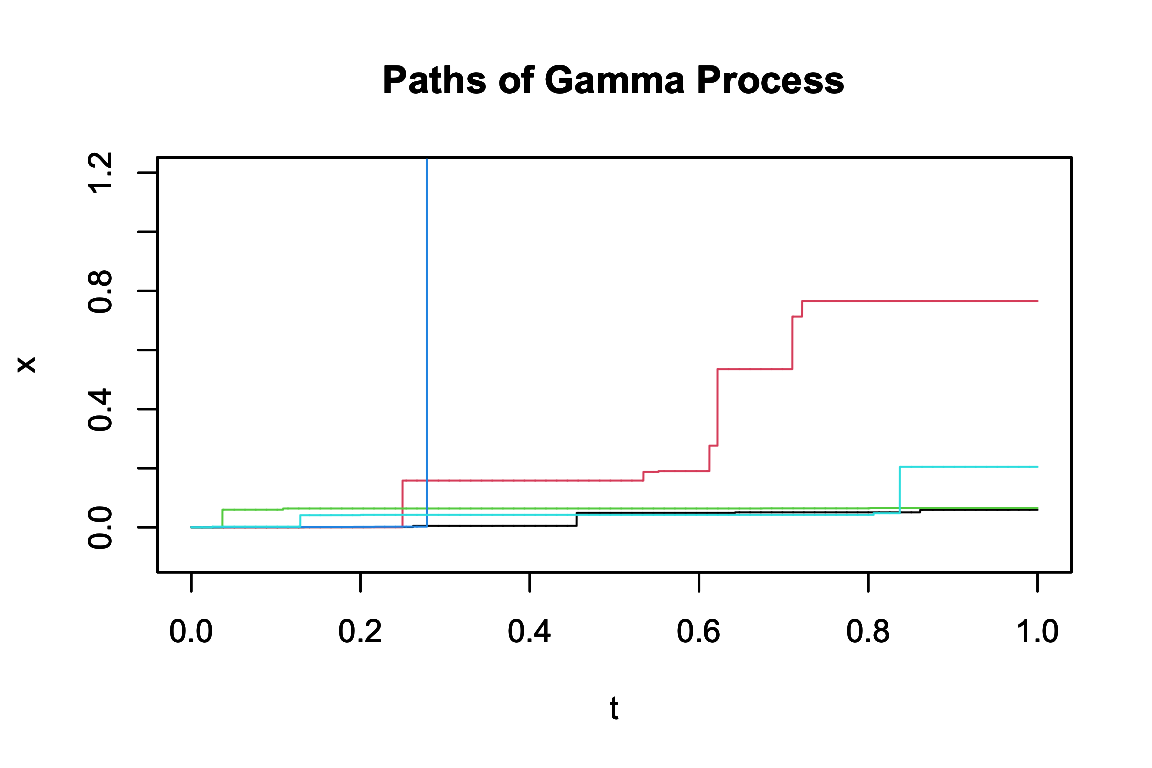
しかし，正のジャンプのみをもち，ジャンプだけで増加していく過程だからと言って，その見本道は区分的に定数ではない．

その Lévy 測度は \(\nu((0,\infty])=\infty\) を満たし，B 型に分類される．従って，\(\mathbb{R}_+\) の稠密部分集合上でジャンプしており，見本道は殆ど確実に，任意の点 \(t\in\mathbb{R}_+\) で非連続である．

Gamma 過程は元々，(Moran, 1959) によりダムの貯水量のモデルとして導入された．

証明

見本道 \(X_\bullet(\omega)\) は，\(\mathbb{R}_+\) のある稠密部分集合 \(A\subset\mathbb{R}_+\) 上でジャンプしているとする：\(\overline{A}=\mathbb{R}_+\)．

このとき，\(\mathbb{R}_+\) の任意の点で \(X_\bullet(\omega)\) は非連続である．

実際，任意の \(t>0\) を取り，ここで連続であるとすると，任意の \(t\) への収束列 \(\{t_n\}\subset\mathbb{R}_+\) について，\(X_{t_n}(\omega)\to X_t(\omega)\) が成り立つ必要があるが，\(t\) は \(A\) の触点でもあるので，これに収束する \(A\) の点列 \(\{t_n\}\subset A\) が取れる．これを特に，下から単調に収束するように取る：\(t_n\searrow t\)．

しかし，\(\nu\) は平均を持つために有界変動ではあり，実際シミュレーションによって得る見本道を見ても，殆どのジャンプは目に見えない．

3.2 Gamma 分布

\(\mathbb{R}\) 上の Gamma 分布 \(\mathrm{Gamma}(\alpha,\nu)\) とは，密度関数 \[ g(x;\alpha,\nu):=\frac{\alpha^\nu}{\Gamma(\nu)}x^{\nu-1}e^{-\alpha x}1_{\mathbb{R}^+}(x) \] が定める分布をいう．\(\alpha\) をレート，\(\nu\) を形状パラメータというのであった．

確率測度の変換則

Gamma 分布と Beta 分布を例に

3.3 Gamma 点過程

\(\sigma\)-有限測度 \(\rho_0\in\mathcal{P}(E)\) と Lévy 測度 \(\nu:=\mathrm{Gamma}(\alpha,0)\)，すなわち \[ \nu(dr):=\frac{e^{-\alpha r}}{r}1_{\mathbb{R}^+}(r)\,dr \] について，\(\lambda:=\rho_0\otimes\nu\) で定まる強度測度を持つ \(E\times\mathbb{R}_+\) 上の Poisson 点過程 \(\xi\) を Gamma 点過程 という．¹⁹

これは \[ \xi(B)\sim\mathrm{Gamma}(\alpha,\rho_0(B)) \] を満たす複合 Poisson 点過程である．\(\rho_0\) のことを形状測度ともいう．

Dirichlet 過程 (Ferguson, 1973) との関係²⁰

\[ \Delta_n:=\left\{\begin{pmatrix}p_1\\\vdots\\p_n\end{pmatrix}\in[0,1]^n\,\middle|\,\sum_{i=1}^np_i=1\right\} \] を \(n-1\)-単体とする．²¹ この上に台を持つ，パラメータ \(\alpha\in(0,\infty)^n\) で定まる密度 \[ f(x)=\frac{\Gamma(\alpha_1+\cdots+\alpha_n)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_n)}x_1^{\alpha_1-1}\cdots x_n^{\alpha_n-1}1_{\Delta_n}(x) \] が定める分布 \(\mathrm{Dirichlet}(n,\alpha)\in\mathcal{P}(\Delta_n)\) を Dirichlet 分布 という．

ここで，\(E\) 上の Gamma 点過程 \(\xi\) は \(\rho_0(E)<\infty\) を満たすとする．このとき，\(E\) の分割 \[ E=B_1\sqcup\cdots\sqcup B_n \] \[ \rho_0(B_i)>0 \] に対して， \[ (\zeta(B_1),\cdots,\zeta(B_n))\sim\mathrm{Dirichlet}(n,\alpha) \] \[ \zeta(-):=\frac{\xi(-)}{\xi(E)} \] が成り立ち，これは \(\xi(E)\) と独立である．

このことをふまえて，\(\rho_0\) が有限であるとき，ランダム確率測度 \[ \zeta(-):=\frac{\xi(-)}{\xi(E)} \] を Dirichlet 過程 という．²²

3.4 Gamma 点過程の Lévy 測度は \(0\) の近傍で発散する

しかし，\(\mathrm{Gamma}(\alpha,0)\) などという分布はなく， \[ \nu(\mathbb{R})=\int^\infty_0r^{-1}e^{-\alpha r}dr=\infty. \]

このとき，任意の \(\rho_0\) で測って正の測度を持つ集合 \(\rho_0(B)>0\;(B\in\mathcal{E})\) に対して，\(\xi\) は殆ど確実に無限個の点を \(B\) 内にもつ．²³

しかし，\(\rho_0(B)<\infty\) ならば \(\xi(B)<\infty\) ではある．すなわち，ジャンプ幅も含めて足し合わせると，収束する．これは，\(\nu\) が平均を持つことによる： \[ \int_0^\infty r\,\nu(dr)=\alpha^{-1}. \]

証明

\[\begin{align*} \xi(B)&=\int^\infty_0\int_Br\,\eta(dsdr)\\ &=\int_B\rho_0(ds)\int^\infty_0r\,\nu(dr)\\ &=\rho_0(B)\alpha^{-1} \end{align*}\]

3.5 従属過程

一般に，\(\xi\) を \(\mathbb{R}^+\) 上の Lévy 測度 \(\nu\in\mathcal{P}(\mathbb{R}^+)\) を持つ一様な複合 Poisson 点過程，すなわち \(\ell_+\otimes\nu\) を強度測度とする \(\mathbb{R}_+\times\mathbb{R}^+\) 上の Poisson 点過程とすると， \[ Y_t(\omega):=\xi(\omega,[0,t]) \] で定まる過程 \(Y\) は，一般に Lévy 測度 \(\nu\) を持つ 従属過程 (subordinator) という．²⁴

3.6 Gamma 計数過程

Lévy 測度 \(\nu\in\mathcal{P}(\mathbb{R}^+)\) を \[ \nu(dr):=\delta\frac{e^{-\gamma r}}{r}dr \] \[ \delta,\gamma>0, \] で与えたとき，付随する従属過程 \(\{Y_t\}\) を Gamma 過程 といい，\(\mathrm{Gamma}(\delta,\gamma)\) で表す．²⁵

これは \(Y_t\sim\mathrm{Gamma}(\gamma,\delta t)\) を満たす Lévy 過程である．

目視できないジャンプが無数に存在することが窺える．

3.7 分散 Gamma 過程

２つの独立な Gamma 過程 \[ X^+\sim\mathrm{Gamma}(\delta,\gamma^-),X^-\sim\mathrm{Gamma}(\delta,\gamma^+) \] に対して， \[ X^0_t=X^+_t-X^-_t \] と表せる Lévy 過程 \(X^0\) を 分散 Gamma 過程 という．²⁶

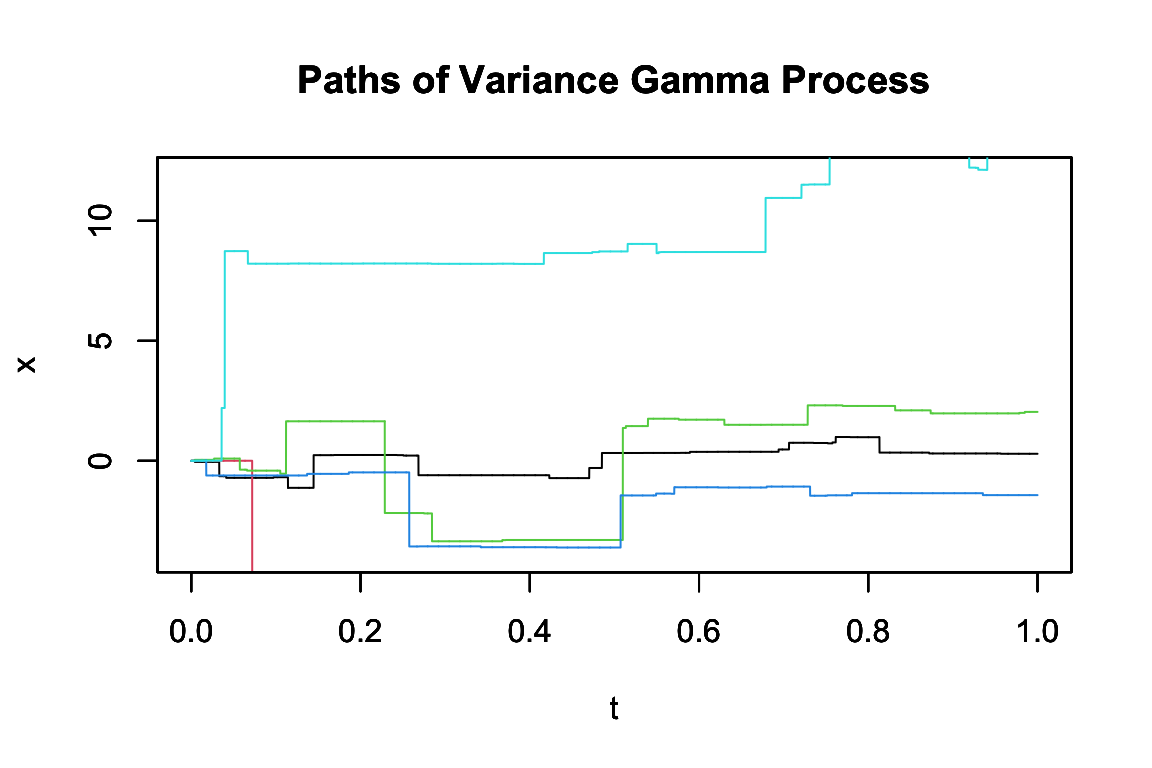
分散 Gamma 過程は，オプション価格の対数のモデルとして，Brown 運動より柔軟なモデルとしても用いられる (Madan et al., 1998)．

これは，Brown 運動の分散が Gamma 分布に従うとして得る過程であるとも見れる．実際，Brown 運動の時間を，Gamma 過程によって変換したものが分散 Gamma 過程である．

実際，Brown 運動 \(B\) とこれと独立な Gamma 過程 \(T\) について， \[ X^0_t=B_{T_t} \] と表せる．²⁷

4 安定過程と Cauchy 過程

4.1 安定分布

4.1.1 定義

定義 (stable)²⁸

• 特性関数 \(f:\mathbb{R}^d\to\mathbb{C}\) が 安定 であるとは，任意の \(n\in\mathbb{N}^+\) に対して，ある \(a_n>0,b_n\in\mathbb{R}^d\) が存在して \[ f(t)^n=f(a_nt)e^{ib_nt} \] が成り立つ無限可分分布の特性関数をいう．
• 確率変数 \(Y\in\mathcal{L}(\Omega;\mathbb{R}^d)\) が 安定 であるとは，任意の \(n\in\mathbb{N}^+\) に対して，ある \(a_n>0,b_n\in\mathbb{R}^d\) が存在して， \[ Y_1+\cdots+Y_n\overset{\text{d}}{=}a_nY+b_n \] を満たすことをいう．

すなわち，安定分布とは， \[ Z_n:=\frac{\sum_{i=1}^nY_i-b_n}{a_n} \] という形の，独立同分布確率変数の正規化された和の列 \(\{Z_n\}\) の分布収束極限として現れ得る分布の全体を指すことになる．²⁹

また，\(a_n\) は \(a_n=n^{1/\alpha}\) という形に限り，この \(\alpha\in(0,2]\) を 安定指数 という．

4.1.2 Lévy 測度の有限性

安定指数 \(\alpha\in(0,2)\) を持つ安定分布の Lévy 測度は非有限であり，平均も持たない．

命題（Lévy 測度の平均）³⁰

\(\mu\in\mathcal{P}(\mathbb{R}^d)\) を \(\alpha\)-安定分布とする．このとき，その Lévy 測度 \(\nu\) について，次は同値：

1. \(\alpha\in(0,1)\) である．
2. \(\nu\) は \(B^d\) 上で平均を持つ： \[ \int_{B^d}\lvert x\rvert\,\nu(dx)<\infty. \]

次も同値：

1. \(\alpha\in(1,2)\) である．
2. \(\nu\) は \(\mathbb{R}^d\setminus B^d\) 上で平均を持つ： \[ \int_{\mathbb{R}^d\setminus B^d}\lvert x\rvert\,\nu(dx)<\infty. \]

4.2 回転対称な安定分布

4.2.1 特性関数の表示

安定分布は無限可分であるため，Lévy-Khintchin 分解を通じた特性関数の形が特徴付けられる．

中でも，（回転）対称な安定分布は特に簡単な表示を持つ：

命題 (Lévy-Khinchin 表示)³¹

\(P\in\mathcal{P}(\mathbb{R}^d)\) は回転対称であるとする．このとき，その特性関数 \(\varphi\) について次は同値：

1. \(\varphi\) は安定である．
2. ある \(c>0\) と \(\alpha\in(0,2]\) が存在して， \[ \varphi(u)=e^{-c\lvert u\rvert^\alpha}. \]

この \(\alpha\) を 安定指数 という．

例（対称な安定分布）

• \(\alpha=2\) の対称安定分布とは，中心化された正規分布である．
• \(\alpha=1\) の対称安定分布とは，中心化された Cauchy 分布である．

中心極限定理のスケーリングレートとしての安定指数

\(a_n\) は従って，中心極限定理を実現するために必要なスケーリングレートを表す．

このことは，一般のエルゴード的な定常過程に対して一般化できる：³²

\(\{X_n\}\) を \(\alpha\)-撹拌的な定常過程，\(\{a_n\}\subset\mathbb{R}^+\) を発散列とし， \[ \frac{1}{a_n}\sum_{j=1}^nX_j-b_n \] は弱収束するとする．この極限分布は安定分布になり，安定指数を \(\alpha\) とする．

このとき，(Karamata, 1933) の意味で緩変動な関数 \(h\) に対して，\(a_n=n^{1/\alpha}h(n)\) と表せる： \[ \lim_{n\to\infty}\frac{h(tn)}{h(n)}=1\quad(t>0). \]

4.2.2 自己相似性

安定指数 \(\alpha\) を持つ回転対称な安定分布 \(Y\) は自己相似性を持つ．

一般に，Hurst 指数 \(H>0\) に関して自己相似的 (self-similar) であるとは，任意の \(a>0\) について \[ (Y_{at})\overset{\text{d}}{=}(a^HY_t) \] を満たすことをいう．

安定指数 \(\alpha\) を持つ回転対称な安定分布 \(Y\) については，\(H=\alpha^{-1}\) と取れる．

Brown 運動は \(H=1/2\) について自己相似である．

また，自己相似な Lévy 過程は，狭義の安定過程に限る．³³

4.3 安定従属過程

\(\alpha\in(0,1)\) の安定指数を持つ安定過程は，従属過程になる．³⁴

例（Lévy 従属過程）³⁵

Lévy 分布 \(\mathrm{Levy}(c):=\mathrm{IG}(c^{1/2},0)\) とは，密度 \[ f(x;c):=\sqrt{\frac{c}{2\pi}}x^{-\frac{3}{2}}e^{-\frac{c}{2x}}1_{\mathbb{R}^+}(x) \] を持つ \(\mathbb{R}\) 上の分布をいう．

これは次の特性関数を持ち，安定指数 \(\alpha=1/2\) を持つ非対称な安定分布である： \[ \varphi(u)=\exp\left(-\sqrt{c\lvert u\rvert}\biggr(1-i\operatorname{sgn}(u)\biggl)\right). \]

安定指数 \(1/2\) の安定従属過程 \(T\) は Lévy 従属過程 とも呼ばれ， \[ T_t\sim\mathrm{Levy}(t^2/2) \] を満たす．

これは，１次元 Brown 運動の到達時刻 \[ T_t:=\inf\left\{s>0\mid B_s=\frac{t}{\sqrt{2}}\right\} \] の過程として現れる．

Lévy 過程は逆正規過程の特殊な場合であり，これは一般の Gauss 過程の到達時刻の過程として現れる．³⁶

例（安定従属過程による従属操作）³⁷

\(\{\tau_t\}_{t\in\mathbb{R}_+}\) を安定指数 \(\alpha\in(0,1)\) を持つ安定従属過程とする．

これと独立な Lévy 過程 \(X\) に対して，従属化 \[ t\mapsto X_{\tau_t} \] は再び Lévy 過程である．

特に，\(X\) を Brown 運動 \(B\) とすると，\(B_{\tau}\) は安定指数 \(2\alpha\) を持つ安定過程になる．

例えば \(\tau_a\) として \[ T_a:=\inf\left\{t\in\mathbb{R}_+\mid B_t=a\right\} \] と取ると，これは安定指数 \(1/2\) を持つ安定従属過程（Lévy 従属過程）の修正である．³⁸

これより，各 \(a\in\mathbb{R}_+\) への到達時刻で止めた Brown 運動の過程 \(a\mapsto B_{T_{a+}}\) は対称な Cauchy 過程になる．

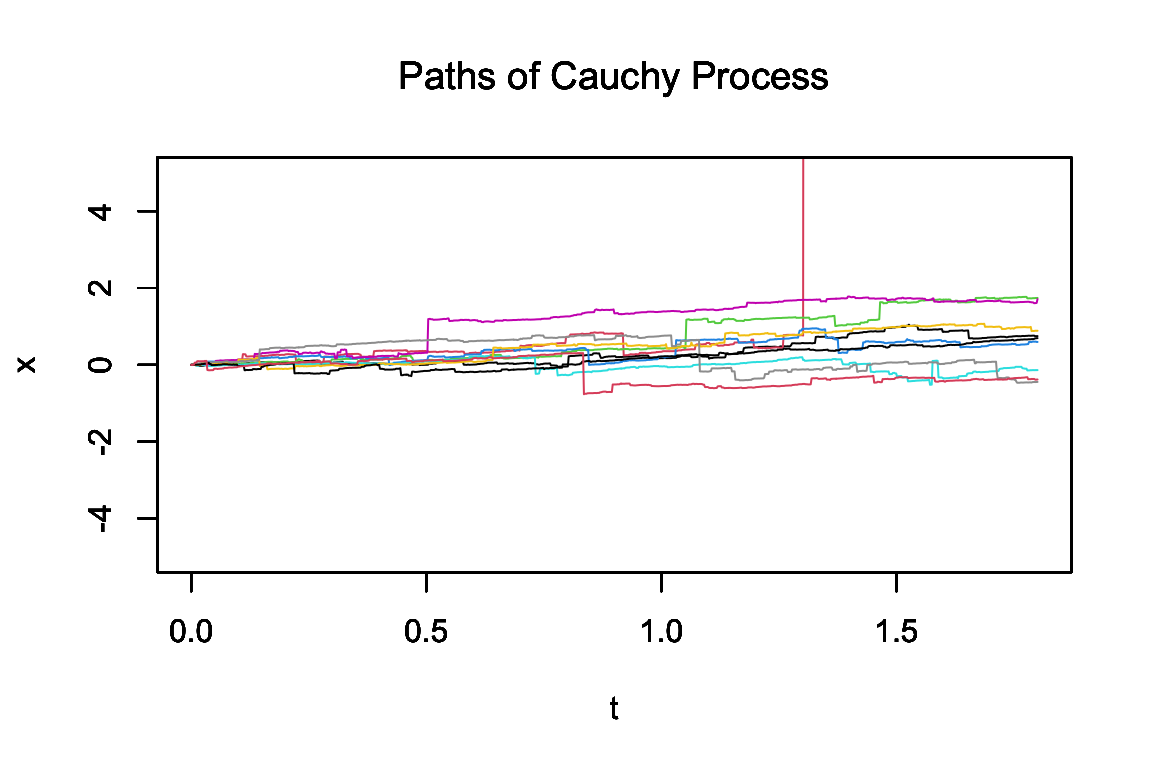
4.4 Cauchy 過程

Cauchy 過程は安定指数 \(\alpha=1\) を持つ狭義の対称安定過程である．³⁹

拡散項を持たないが，Lévy 測度は平均を持たず（命題 4.1.2），C 型の Lévy 過程である．

すなわち，殆ど確実に，任意の区間上で有界変動でない．

References

Applebaum, D. (2009). Lévy processes and stochastic calculus,Vol. 116. Cambridge University Press.

Baudoin, F. (2014). Diffusion processes and stochastic calculus,Vol. 16. European Mathematical Society.

Böttcher, B., Schilling, R., and Wang, J. (2013). Lévy matters III: Lévy-type processes: Construction, approximation and sample path properties,Vol. 2099. Springer Cham.

Dudley, R. M. (2002). Real analysis and probability,Vol. 74. Cambridge University Press.

Embrechts, P., and Maejima, M. (2002). Selfsimilar processes. Princeton University Press.

Ferguson, T. S. (1973). A bayesian analysis of some nonparametric problems. The Annals of Statistics, 1(2), 209–230.

Ghosal, S., and van der Vaart, A. (2017). Fundamentals of nonparametric bayesian inference,Vol. 44. Cambridge University Press.

Iacus, S. M., and Yoshida, N. (2018). Simulation and inference for stochastic processes with YUIMA: A comprehensive r framework for SDEs and other stochastic processes. Springer Cham.

Ibragimov, I. A., and Linnik, Y. V. (1971). Independent and stationary sequences of random variables. Groningen, Wolters-Noordhoff.

Ito, K. (1941). On stochastic processes (i). Japanese Journal of Mathematics :transactions and Abstracts, 18, 261–301.

Karamata, J. (1933). Sur un mode de croissance régulière. Théorèmes fondamentaux. Bulletin de La Société Mathématique de France, 61, 55–62.

Khinchin, A. Ya., and Lévy, P. (1936). Sur les lois stables. Comptes Rendus de l’Académie Des Sciences, 202, 374–376.

Kingman, J. F. C. (1992). Poisson processes. Clarendon Press.

Last, G., and Penrose, M. (2017). Lectures on the poisson process. Cambridge University Press.

Le Gall, J.-F. (2016). Brownian motion, martingales, and stochastic calculus,Vol. 274. Springer Cham.

Loéve, M. (1977). Probability theory i,Vol. 45. Springer New York.

Lowther, G. (2011). Properties of lévy processes.

Madan, D. B., Carr, P. P., and Chang, E. C. (1998). The Variance Gamma Process and Option Pricing. Review of Finance, 2(1), 79–105.

Moran, P. A. P. (1959). The theory of storage. London: Methuen; Co. Led. New York: Wiley; Sons, Inc.

Nualart, D., and Nualart, E. (2018). Introduction to malliavin calculus,Vol. 8. Cambridge University Press.

Osswald, H. (2012). Malliavin calculus for lévy processes and infinite-dimentional brownian motion,Vol. 191. Cambridge University Press.

Protter, P. E. (2005). Stochastic integration and differential equations,Vol. 2. Springer Berlin, Heidelberg.

Revuz, D., and Yor, M. (1999). Continuous martingales and brownian motion. Springer Berlin, Heidelberg.

Rocha-Arteaga, A., and Sato, K. (2019). Topics in infinitely divisible distributions and lévy processes, revised edition. Springer Cham.

Rogers, L. C. G., and Williams, D. (2000). Diffusions, markov processes, and martingales. Volume i: foundatinos. Cambridge University Press.

Sato, K. (2013). Lévy processes and infinitely divisible distributions. Cambridge University Press.

Shiryaev, A. N. (2016). Probability-1,Vol. 95. Springer New York.

伊藤清. (1991). 確率論. 岩波書店.

佐藤健一. (1990). 加法過程,Vol. 33. 紀伊国屋書店.

佐藤健一. (2011). レヴィ過程による確率積分と無限分解可能分布. 数学, 63(2), 161–181.

Footnotes

1. (Nualart and Nualart, 2018, p. 158) 定義9.1.1，(Sato, 2013, p. 3) 定義1.6，(Rocha-Arteaga and Sato, 2019, pp. 12–13) 定義1.31に倣った．(Protter, 2005, p. 20) では(2)の\(D\)-過程という部分がないのみで，定理30 (Protter, 2005, p. 21) で常に\(D\)-修正が取れることを示している．(Le Gall, 2016, p. 175) 6.5.2節も同様の取り扱いである．(伊藤清, 1991, p. 306) は時間的一様性を所与のものとはせず，(1), (2), (3), (5)のみをLévy過程の定義としており，さらに(4)も満たすものを 一様Lévy過程 という．(Baudoin, 2014, pp. 89–90) 定義3.40では(5)がない．(Böttcher et al., 2013, p. 14) 例1.17では(1),(2)がない．(Osswald, 2012, pp. 258–259) は(1), (3), (4)を定義としている．(Applebaum, 2009, p. 43) は(1), (3), (4), (5)を定義としている．(佐藤健一, 1990) では全く同じものを加法過程と呼ぶが，(佐藤健一, 2011) は完全に一致する語用法をする（加法過程に確率連続性を課している点を除く）．

2. (Sato, 2013, p. 47) 定理9.1 参照．

3. (Sato, 2013, p. 51) 定理9.7参照．

4. (Dudley, 2002, p. 327) 定理9.8.3，(Sato, 2013, p. 37) 定理8.1，(Rocha-Arteaga and Sato, 2019, p. 11) 定理1.28，(Baudoin, 2014, p. 91) 定理3.46，(Applebaum, 2009, p. 29) 定理1.2.14 など参照．

5. Gauss 共分散の用語は (Sato, 2013, p. 38) 定義8.2．Khintchine 測度は (Loéve, 1977, p. 343)，(Applebaum, 2009, p. 31)，(Böttcher et al., 2013, p. 33)，(Baudoin, 2014, p. 92) など．

6. (Loéve, 1977, p. 343)

7. (Sato, 2013, p. 39) 注8.4．

8. 特性測度の名前は (Revuz and Yor, 1999, p. 478) 演習 XII.1.18 など．命題は (Sato, 2013, p. 53) 注9.9も参照．

9. (Sato, 2013, p. 120) 定理19.2より．(Protter, 2005, p. 31) 定理42 は Lévy 過程に限って示している．(1)は (伊藤清, 1991, p. 313) 補題5.3でも解説されている．(Protter, 2005, p. 26)定理35も参照．

10. この分類は (Sato, 2013, p. 65) 定義11.9に倣った．

11. (Sato, 2013, p. 140) 定理21.9 参照．

12. (Sato, 2013, p. 135) 定理21.1．

13. (Lowther, 2011) 定理１，(Sato, 2013, p. 135) 定理21.2．

14. (Sato, 2013, p. 136) 定理21.3．

15. (Applebaum, 2009, p. 52)，(Baudoin, 2014, p. 95) 定義3.50，(Sato, 2013, p. 137) 定義21.4，(Iacus and Yoshida, 2018, p. 171) に倣った．(Kingman, 1992, p. 88) 8.4節，(Last and Penrose, 2017, p. 156) 例15.7 は命題の条件2の方を定義に用いている．

16. (Sato, 2013, p. 137) 定理21.5．

17. (Sato, 2013, p. 138) も参照．

18. (Lowther, 2011) 定理２，(Sato, 2013, p. 140) 定理21.9．

19. 定義は (Last and Penrose, 2017, p. 155) 例15.6 に倣った．

20. (Ghosal and van der Vaart, 2017, p. 562) 命題G.2.(i)，(Last and Penrose, 2017, p. 163) 演習15.1，(Kingman, 1992, pp. 92–) 9.2節．

21. \(n=2\) を取ると１単体（線分），\(n=3\) と取ると２単体（三角形）を得る．

22. (Kingman, 1992, p. 93)，(Ghosal and van der Vaart, 2017, p. 59) 定義4.1．

23. \(\lambda(B)=\rho_0(B)\nu(\mathbb{R})=\infty\) となるためである．(Last and Penrose, 2017, p. 163) 演習15.2も参照．

24. (Kingman, 1992, p. 88) 8.4節，(Last and Penrose, 2017, p. 156) 例15.7 などの用語法．一般に subordinator とは，単調増加な Lévy 過程をいう (Sato, 2013, p. 137) 定義21.4，(Baudoin, 2014, p. 95) 定義3.50，(Iacus and Yoshida, 2018, p. 171)．これは，時間変数に関する変数変換を subordination と呼び，その際の変数変換に使えるためである．

25. 記法は (Iacus and Yoshida, 2018) による．(Applebaum, 2009, pp. 54–55) 例1.3.22，(Protter, 2005, p. 33) 例４も参照．

26. (Iacus and Yoshida, 2018, p. 160) に倣った．

27. (Lowther, 2011)，(Applebaum, 2009, p. 59) 例1.3.31 も参照．

28. (Revuz and Yor, 1999, p. 116) 定義III.4.1，(Sato, 2013, p. 69) 定義13.1，(Shiryaev, 2016, p. 416) 定義3.6.2，(Loéve, 1977, p. 338)．

29. (Shiryaev, 2016, p. 416) 定理3.6.3 も参照．

30. (Sato, 2013, p. 80) 命題14.5．

31. (Sato, 2013, p. 86) 定理14.14．(Shiryaev, 2016, p. 419) 定理3.6.4，(Loéve, 1977, p. 339)，(Dudley, 2002, p. 328) 定理9.8.4 は \(d=1\) の場合．

32. (Ibragimov and Linnik, 1971, p. 316) 定理18.1.1 も参照．

33. 狭義の安定過程とは，\(b_n\equiv0\) と取れることをいう (Sato, 2013, p. 69) 定義13.1．(Embrechts and Maejima, 2002)，(Applebaum, 2009, p. 51) 例1.3.14 も参照．

34. (Revuz and Yor, 1999, p. 116)，(Sato, 2013, p. 138) 例21.7，(Applebaum, 2009, p. 53) 例1.3.18 も参照．

35. (Applebaum, 2009 @/53) 例1.3.19 も参照．

36. (Applebaum, 2009, p. 54) 例1.3.21 も参照．

37. (Revuz and Yor, 1999, p. 116)，(Rogers and Williams, 2000, p. 133) も参照．

38. (Revuz and Yor, 1999, p. 107) 命題III.3.9 も参照．

39. (Sato, 2013, p. 87) 例14.17．