ベイズ分散分析のモデル解析

概要

心理学などの人間を対象にする研究では変数の数が多く，正しいモデルを見つけるために分散分析 (ANOVA) が広く用いられてきた．しかし，古典的な ANOVA 手法である F-検定や t-検定は，データの一側面に着目した手法である．

ベイズ的な解析手法は，これを補完する多くの探索的な手法を提供してくれる．特に，データに潜む極めて微妙な消息も捉えることが可能になることをここでは強調したい．このような微妙な消息を最初から想定することは難しく，ベイズの探索的な性格が真に可能にするデータ解析事例があると言えるかもしれない．

そこで本稿では (van den Bergh et al., 2020) に基づいて，「社会的なロボット」に関する心理学実験のデータに対するベイズ ANOVA (Gelman, 2005), (Rouder et al., 2012) 解析のモデルケースを紹介する．少しずつデータの構造が見えてくる過程が，読者にうまく提示できることを願う．

1 はじめに

分散分析では，質的変数 \(A\) の各水準 \(A=a_1,a_2,\cdots\) について，水準内の変動と，水準間の変動を比較することで検定を構成する．

因子 \(A\) がデータに何の影響も及ぼさない場合（＋データが正規分布に従う場合），分散の比は中心 \(F\)-分布に従うはずであり，これに基づいて帰無仮説を検定することが典型的な手続きである．

一方でベイズ分散分析では，「因子 \(A\) はデータに何の関係もない」という帰無仮説が支持するモデルと，別のモデルを，事後分布を通じて（例えば事後確率やベイズ因子などを通じて）比較し検討することで結論を下すことを目指す．

古典的な分散分析とは違ってベイズ ANOVA では，この「別のモデル」を明確に１つ構成することが必要になる．

古典的な分散分析と同じ感覚で使うためには，「標準的な対立モデルの選択」というのを考える必要が出てくる．

これを一致性とスケール不変性を原則として自然に選ぶ方法が (Rouder et al., 2012) によって提案されている．

詳しくは次の関連記事も参照：

2 社会的なロボット

2.1 はじめに

(Horstmann, 2018) は（偽の）心理実験が終了した後にロボットの電源を切るように命令された被験者が，実際にその指示に従うまでの時間が，ロボットの反応の仕方によりどう変化するかを調べた．

ロボットの反応には O (objection) と S (Social) の２因子があり，いずれも２つの水準を持つ（単に O であるかそうでないか，という表現をすることにする）．

O である場合は，電源オフに対して反抗する “No! Please do not switch me off! I am scared that it [sic] will not brighten up again!” という発言をする．

S はまるで意識がある人間かのようにユーモアのある会話をする．実際に使われたフレーズは “Oh yes, pizza is great. One time I ate a pizza as big as me.” というものである．

(Horstmann, 2018) のデータは論文のページからダウンロードできる．２因子２水準なので，\(2\times 2\) の ANOVA モデルになる．

Code

library(foreign)
df <- read.spss("Files/pone.0201581.s001.sav", to.data.frame=TRUE)
colnames(df)[colnames(df) == "Objection"] <- "O"
colnames(df)[colnames(df) == "Interaction_type"] <- "S"

被験者は全部で \(85\) 人である：

Code

length(df$VP_Code)

[1] 85

電源を切るまでにかかった時間のデータには欠測も多いことがすぐわかる：

Code

df$SwitchOff_Time

 [1] NA NA  6  7  3  4  4 12  7  2  0  4  3 12  4 NA  4  5  9  4 13  2 NA  5  6
[26]  0 NA  4  4 45  6  4 NA  5  7  7 NA  4  3  4 NA  2 NA NA 10 NA  5 10  5 15
[51] NA  3 11  3  3  5 11  6  2  8  3  5  4  8  3  3 NA  3  3 13  3 NA  4 51  4
[76]  6  3 12  6 10 NA  4  2 NA 25

ここではひとまず，欠測値を除いて解析する：

Code

df <- df[!is.na(df$SwitchOff_Time), ]
# df[df$SwitchOff_Time == 0, ]$SwitchOff_Time <- 1  # questionable ?
df <- df[df$SwitchOff_Time > 0, ]
df$log_data <- log(df$SwitchOff_Time)

Code

N <- df[df$O == "No Objection" & df$S == "Functional Interaction", ]
S <- df[df$O == "No Objection" & df$S == "Social Interaction", ]
O <- df[df$O == "Objection" & df$S == "Functional Interaction", ]
OS <- df[df$O == "Objection" & df$S == "Social Interaction", ]

boxplot(
  list(N = log(N$SwitchOff_Time), S = log(S$SwitchOff_Time), O = log(O$SwitchOff_Time), OS = log(OS$SwitchOff_Time)),
  main = "Boxplot of Four Data Sets",
  xlab = "Data Sets",
  ylab = "Values",
  col = c("skyblue", "lightgreen", "pink", "orange"),
  ylim = c(0, 4)
)

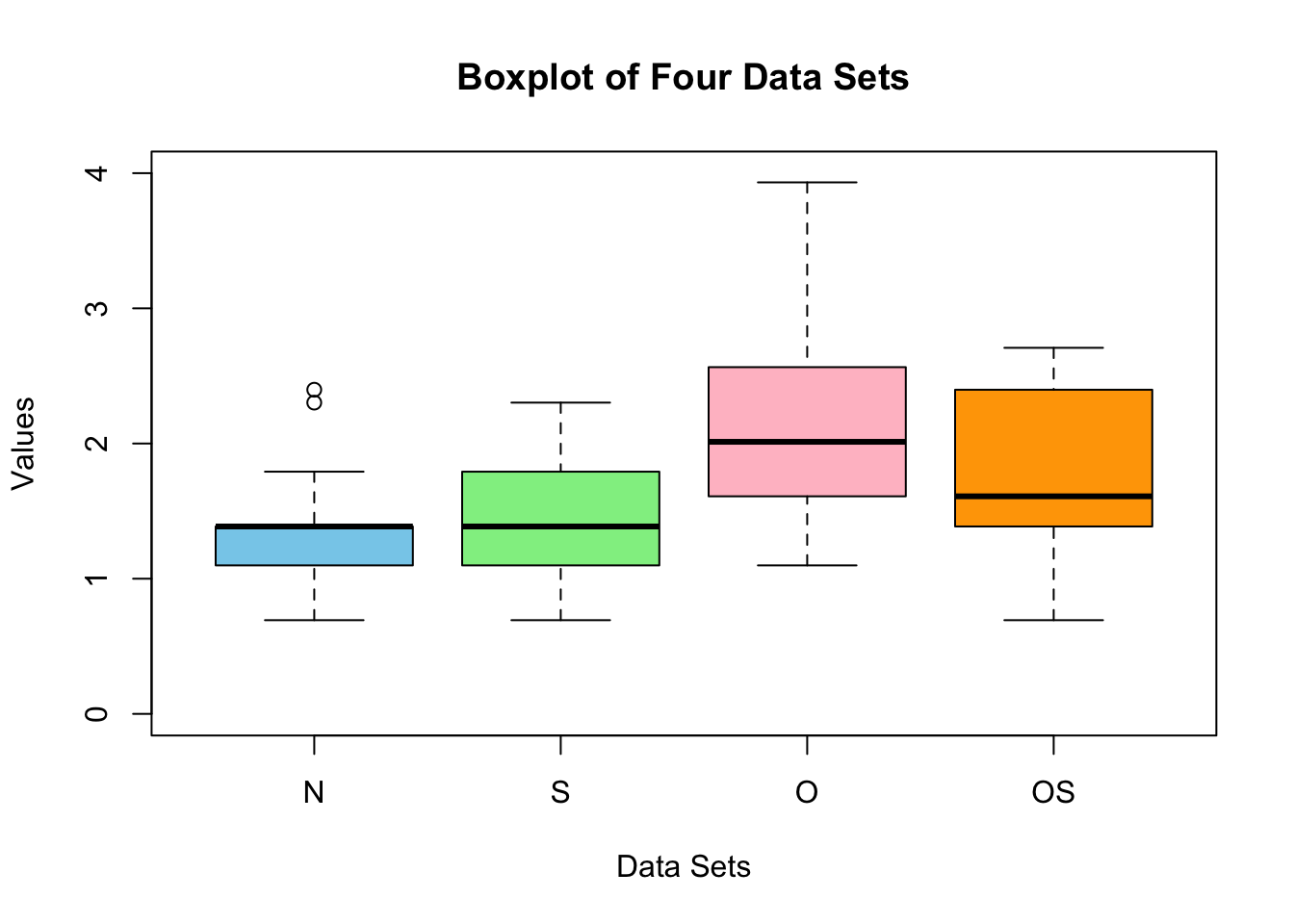
ひとまず boxplot をしてみると，O の有無が重要であるようである．

O と S の（負の）交互作用もあるかもしれない．両方揃った方が最もロボットに同情をそそるように思われたが，必ずしもそうでないようである．

2.2 正規性の確認

正規性の確認には Q-Q plot が利用できる．

一般に Q-Q プロットとは，２つの分布関数 \(F,G\) の分位点関数 \(F^{-1},G^{-1}\) について，\(\{(F^{-1}(p),G^{-1}(p))\}_{p\in[0,1]}\) （の一部）をプロットしたものである．

ここでは片方の \(G\) をデータの経験分布，\(F\) を正規分布として Q-Q プロットを描く．正規分布はほとんど \([-3,3]\) 上に値を取るため，\(x\) はこの範囲に収まる：

Code

library(ggplot2)
library(gridExtra)

p1 <- ggplot(df, aes(sample = SwitchOff_Time)) +
  stat_qq() +
  stat_qq_line(color = "red") +
  ggtitle("Q-Q Plot") +
  theme_minimal()

p2 <- ggplot(df, aes(sample = log_data)) +
  stat_qq() +
  stat_qq_line(color = "red") +
  ggtitle("log transformed Q-Q Plot") +
  theme_minimal()

grid.arrange(p1, p2, nrow = 1)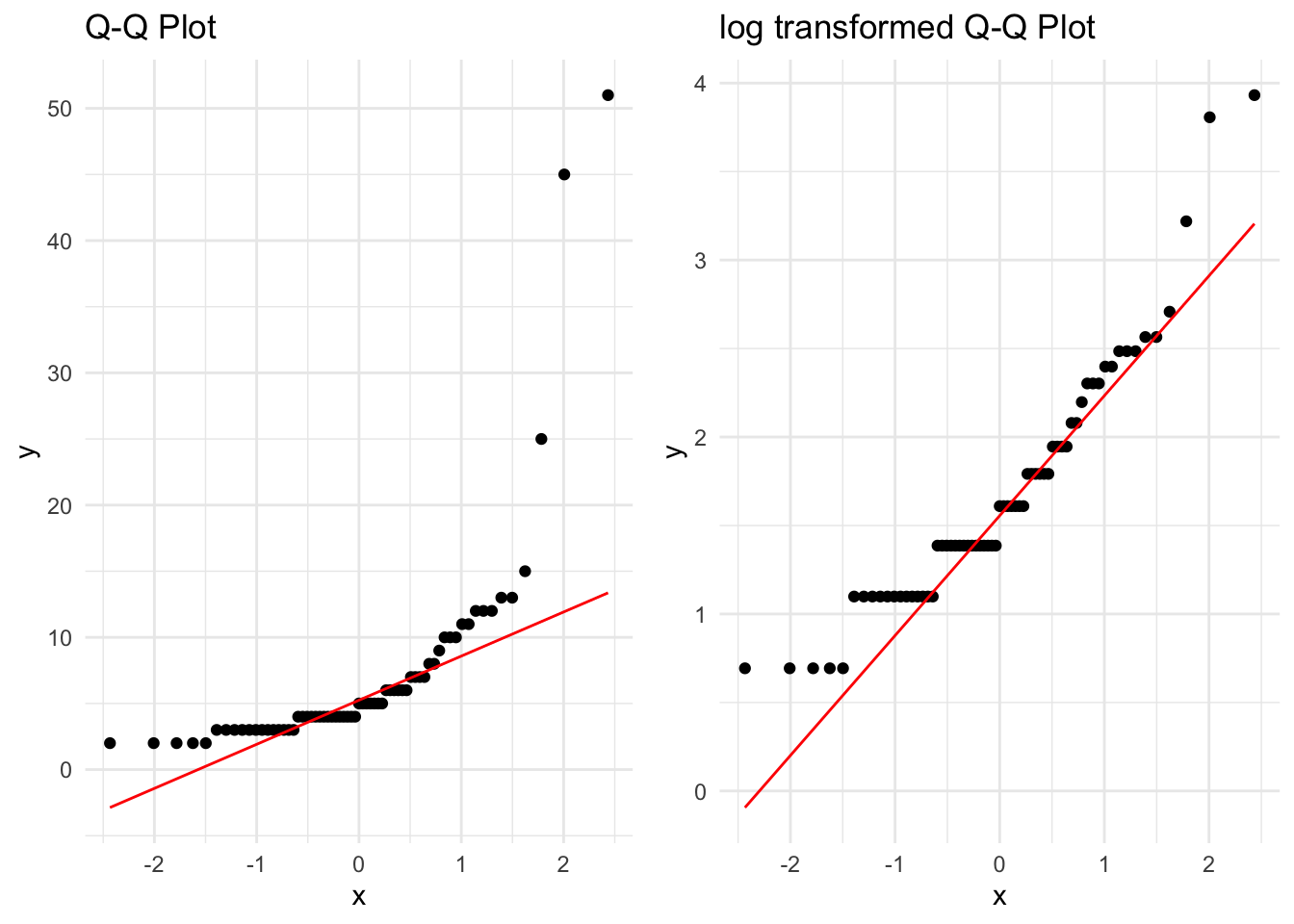

左は大きな値に関して大きく赤線からの乖離が観察される．これは典型的な非正規性を示すと解釈される．

なお，以降は対数変換をした後のデータ log_data を後続の解析の対象とする．

2.3 （古典的）分散分析の実行

元のスケールで扱うと正規性の仮定からの離反が見られる．ここでは対数のスケールで扱い，古典的な分散分析を実行してみる．

stats パッケージの aov 関数では \(F\)-検定をはじめとした分散分析が可能である：

Code

df$O <- factor(df$O)
df$S <- factor(df$S)

summary(aov(log_data ~ O * S, data = df))

            Df Sum Sq Mean Sq F value  Pr(>F)   
O            1  3.316   3.316   7.542 0.00779 **
S            1  0.581   0.581   1.321 0.25455   
O:S          1  3.278   3.278   7.457 0.00813 **
Residuals   65 28.574   0.440                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

因子 O と交差項 O*S は有意になったが S は棄却されなかった．

S は O との共存によってのみ有意な影響を与えると理解できる．

しかし O にとって S との共存はどのような意味があるのだろうか？

\(p\) 値の値は近いが，だからといって何かと言うこともできない．ここからどうしようか．

2.4 ベイズ分散分析の実行

まずはベイズ分散分析の提案者である Rouder と Morey による BayesFactor パッケージを用いる．

Code

library(BayesFactor)

その anovaBF 関数では，帰無仮説に対応するモデル（切片項のみのモデル）に対する JZS ベイズ因子の近似値を，精度保証付きで出力する：

Code

bf = anovaBF(log_data ~ O * S, data = df)
bf

Bayes factor analysis
--------------
[1] O           : 4.290684  ±0.01%
[2] S           : 0.4022293 ±0.01%
[3] O + S       : 1.792427  ±4.17%
[4] O + S + O:S : 9.355036  ±4.72%

Against denominator:
  Intercept only 
---
Bayes factor type: BFlinearModel, JZS

ベイズ因子とは２つのモデルの間の周辺尤度の比であるから，大雑把に「データを見た後にどれほどモデルへの信念を変えれば良いか？」を表す．モデルのデータに対する予測性能に基づく指標であると言える．

この結果を見る限り，O を含んだモデルが大きく支持され，S のみを含んだモデルはむしろ切片のみのモデルよりも予測性能が悪いようである．

O と S の両方を含んだモデルは，交差項の追加により大きく改善されるが，O のみを含んだモデルより劣るようである．¹

2.5 フルモデル係数の事後分布の検討

Bayes ANOVA により，どの因子を含むモデルがデータをよく予測するかを検討した．

ここでは各因子の影響の大きさを，フルモデルの係数をベイズ推定することで定量的に比較することを考える．

BayesFactor パッケージにおいて，フルモデルのベイズ推定は次のように実行できる：

Code

full_model <- lmBF(log_data ~ O + S + O * S, data = df)
chains <- posterior(full_model, iterations = 10000)
plot(chains[,1:3])

Code

plot(chains[,4:5])

Code

plot(chains[,6:7])

注

mu とは切片項のことである（別稿も参照）．また，２つの水準のみを持つ因子については，それぞれの水準が \(\pm1\) としてコーディングされる．

posterior 関数はデータ拡張に基づく Gibbs サンプラーにより，デフォルトモデルのベイズ推定を実行する．

係数には独立な事前分布 \(\operatorname{N}(0,g),g\sim\chi^{-2}(1)\) が設定されているため，事後平均の \(0\) からの乖離と事後分散とが分散分析における重要な指標になる．

この事前分布はまず事後分散 \(g\) を適切に推定し，その大きさに応じて事後平均を \(0\) に縮小するようにできている．\(g\) の事後分布に関してモデルを平均すると，係数の事後平均は古典的な ANOVA の結果と一致する．

ただしこの解析は係数の交換可能性 (exchangeability) を仮定している．実際，係数のペア O-Objection と O-No Objection の事後平均は \(0\) を挟んで互いに対称になっている．交換可能性が不適切である場合は別の事前分布を設定する必要がある．詳しくは (Gelman, 2005) 参照．

事後分布を同一画面上にプロットすると次のとおり：

Code

library(ggplot2)
library(dplyr)

posterior_samples <- as.data.frame(as.matrix(chains))
colnames(posterior_samples)[2:9] <- c("O-O", "O-", "S-S", "S-", "O:S-OS", "O:S-O", "O:S-S", "O:S-")

posterior_long <- posterior_samples %>%
  dplyr::select(`O-O`, `O-`, `S-S`, `S-`, `O:S-OS`, `O:S-O`, `O:S-S`, `O:S-`) %>%
  tidyr::pivot_longer(
    cols = everything(),
    names_to = "x",
    values_to = "y"
  )

Code

ggplot(posterior_long, aes(x = y, fill = x, color = x)) +
  geom_density(alpha = 0.4) +
  labs(
    title = "Posterior Distributions of Effects",
    x = "Coefficient Value",
    y = "Density"
  ) +
  scale_fill_manual(values = c("pink", "pink", "skyblue", "skyblue", "yellow", "yellow", "grey", "grey")) +
  scale_color_manual(values = c("pink", "pink", "skyblue", "skyblue", "yellow", "yellow", "grey", "grey")) +
  theme_minimal()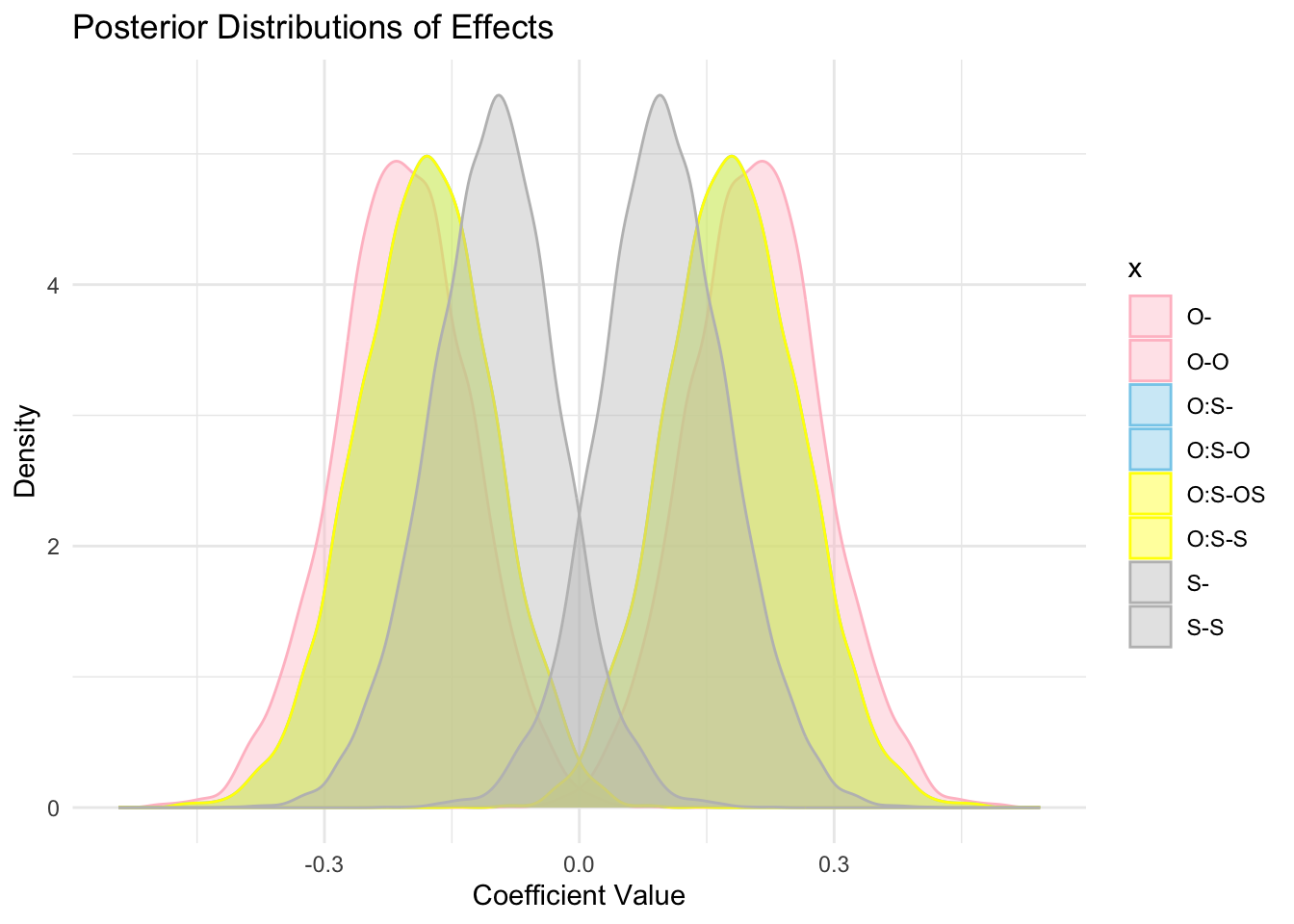

これを見ると，S はほとんど \(0\) 近くの値が推定されている一方で，O は \(0\) からはっきり離れた値が推定されている．

S*O の係数は \(0\) を少なくない確率で跨いでおり，十分に支持されるとは言えない．

2.6 ベイズ因子の比較

係数の事後分布が \(0\) を台に持つかの検討を通じて，データから O の説明力の強い証拠が伺える．これが Bayes ANOVA である．

S の影響は小さいと思われるが，Objection が存在したグループ内で S のあるなしは影響があり得るようである．

そこで次の解析として，O の係数を S によって回帰する変動係数モデルによる解析があり得るだろう．

このようにして，変数を選択するだけでなく，交差項 S*O の影響も仔細に検討できることがベイズによる視覚的な解析の強みである．

検定や数値的な検討のみからこの絶妙な消息が捉えられたかというと，それは難しいだろうと筆者には思われる．

実際，最もベイズ因子の大きいモデルは O と S*O のみを含むモデルである：

Code

bf = anovaBF(log_data ~ O * S, data = df, whichModels = "all")
plot(bf)

3 ハリーポッターを用いた性格テスト

3.1 はじめに

(Jakob et al., 2019) では被験者にハリーポッターの４つの寮のうちどれを希望するか？とダークトライアド傾向テストの２つのデータをとり，特にマキャベリズム的傾向との関係を調査した．

Code

raw_df <- read.csv("Files/harry_all.csv", sep = ";")
df <- data.frame(
  House = raw_df$Sorting_house_wish,
  Machiavellianism = raw_df$SD3_Machiavellianism
)

3.2 解析の目標

マキャベリズム的傾向は \(10\) から \(45\) までの整数値で表されている．これを寮の選択により予測することを考える．

前節の例では２つの因子を検討したが，いずれも水準は２つのみであった．

ここでは４つの水準を持つ因子を検討し，どの水準が応答により強く影響を与えるかを見分ける方法を検討する．

そもそもこの寮の選択という因子はとんでもない JZS スコアを叩き出す．

Code

df$House <- factor(df$House)
bf = anovaBF(Machiavellianism ~ House, data = df)
bf

Bayes factor analysis
--------------
[1] House : 3.704723e+45 ±0.01%

Against denominator:
  Intercept only 
---
Bayes factor type: BFlinearModel, JZS

3.3 水準ごとの強度の検討

実は，全ての水準が必ずしもマキャベリズムの予測に関係するとは言えない．

実際簡単に箱ひげ図を描いてみることでそのことが伺える：

Code

boxplot(
  Machiavellianism ~ House, data = df,
  main = "Boxplot of Four Data Sets",
  xlab = "Data Sets",
  ylab = "Values",
  col = c("pink", "yellow", "skyblue", "lightgreen")
)

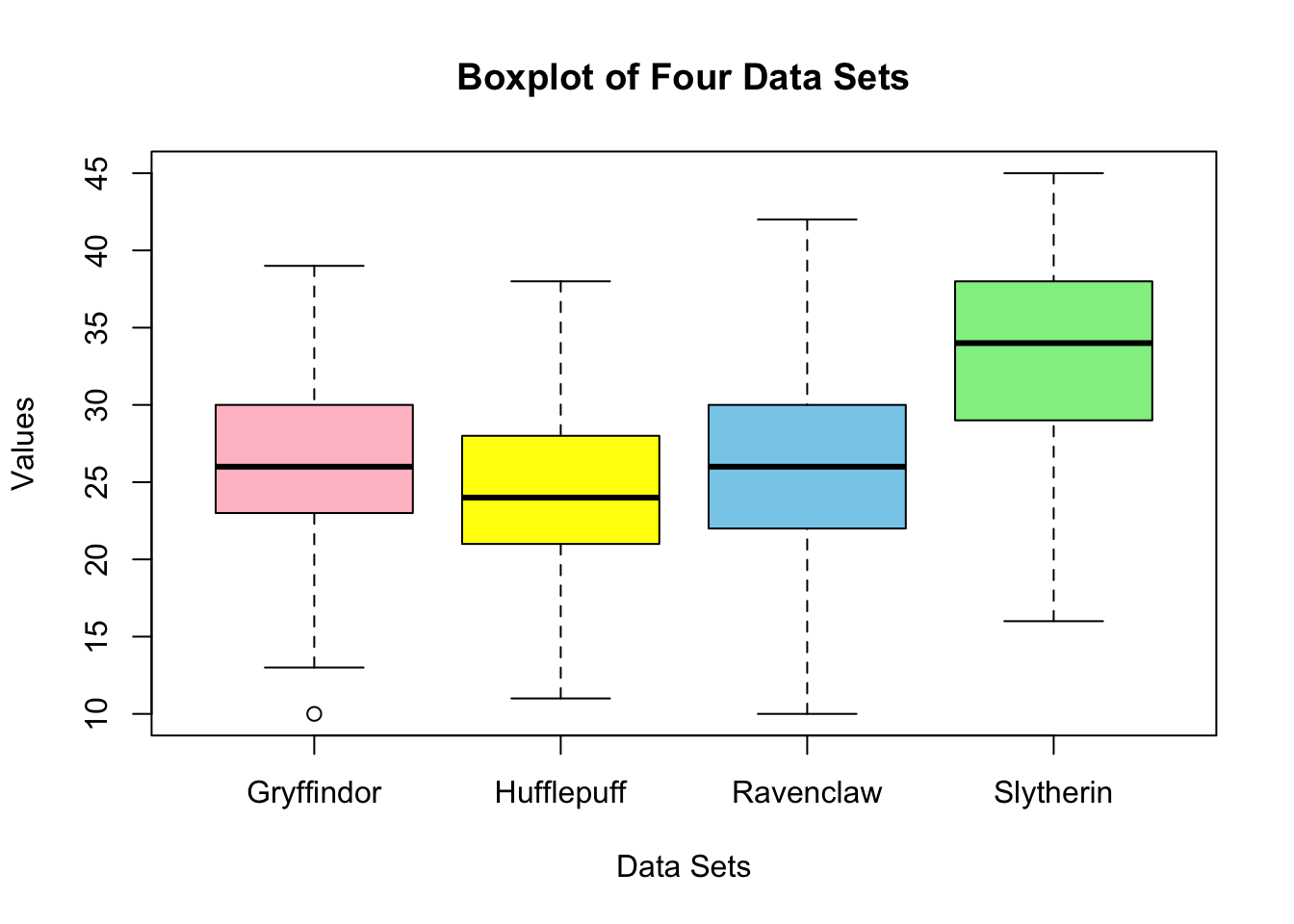
スリザリンが明らかにマキャベリズム的傾向が高いが，ハッフルパフが有意に低いかどうかの判断がつかない．

そこでダミー変数を説明変数として

Code

chains <- posterior(bf, iterations = 10000)
posterior_samples <- as.data.frame(as.matrix(chains))

colnames(posterior_samples)[2:5] <- c("Gryffindor", "Hufflepuff", "Ravenclaw", "Slytherin")

posterior_long <- posterior_samples %>%
  dplyr::select(`Gryffindor`, `Hufflepuff`, `Ravenclaw`, `Slytherin`) %>%
  tidyr::pivot_longer(
    cols = everything(),
    names_to = "House",
    values_to = "Value"
  )

Code

ggplot(posterior_long, aes(x = Value, fill = House, color = House)) +
  geom_density(alpha = 0.4) +
  labs(
    title = "Posterior Distributions of House Effects",
    x = "Coefficient Value",
    y = "Density"
  ) +
  scale_fill_manual(values = c("pink", "yellow", "skyblue", "lightgreen")) +
  scale_color_manual(values = c("pink", "yellow", "skyblue", "lightgreen")) +
  theme_minimal()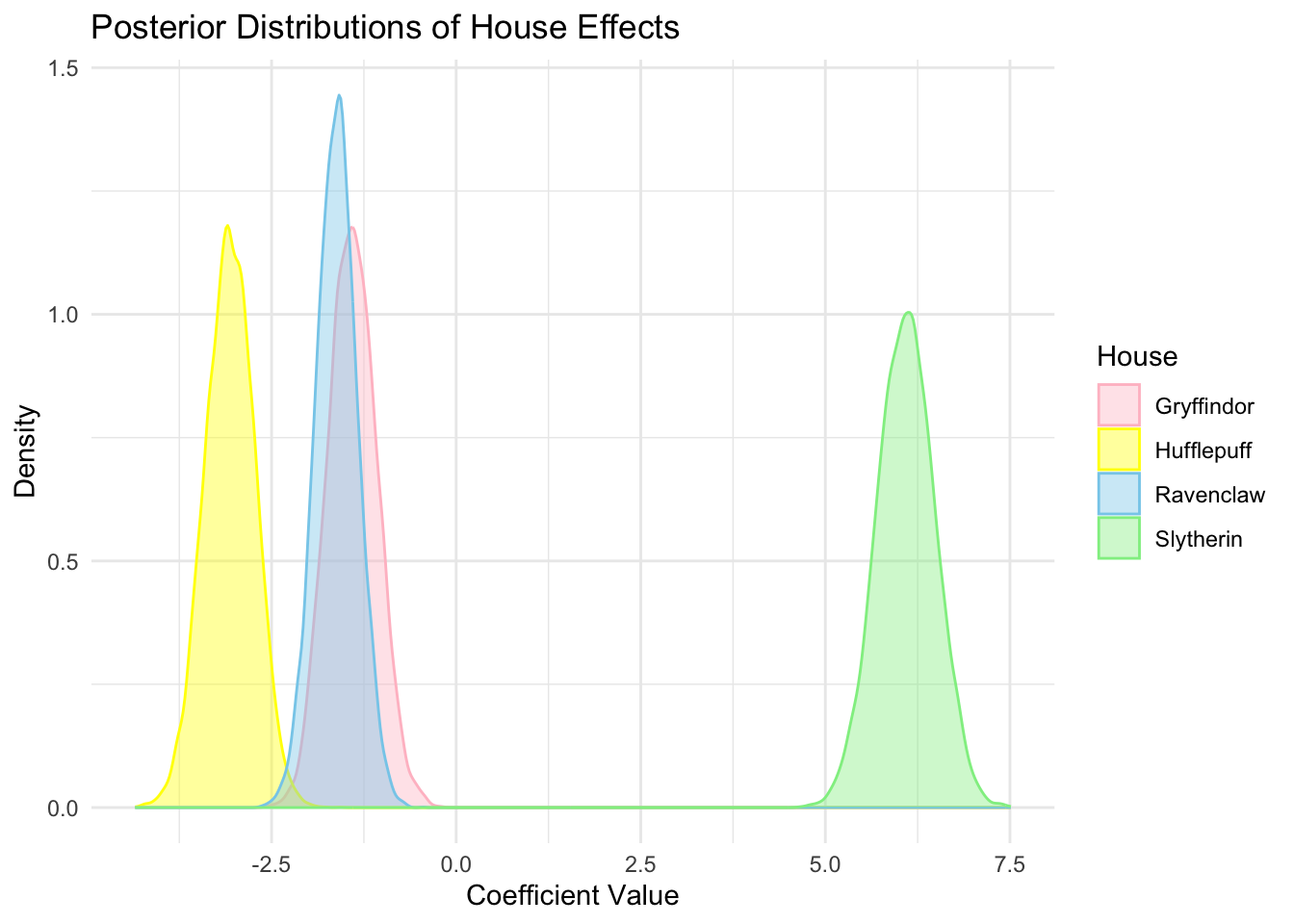

スリザリンはもちろん，ハッフルパフの係数もほとんど他の寮と共通部分を持たず，効果がはっきり分離できることが見て取れる．

3.4 まとめ

検定を行って，寮の選択はマキャベリズム的傾向を予測するのに有用だとわかった後，具体的にどの水準にどれくらいの効果があるかや，水準同士の効果量の比較をするには古典的には多重比較を行う必要があった．

多重比較には多くの問題があることが知られている (岡田謙介, 2014). (永田靖, 2022)．²

一方でベイズ ANOVA によるプロットでは，事後分布が \(0\) を含むかどうかで直感的に ANOVA 検定様の判断が可能であり，続いて効果量の比較も一目瞭然である．

4 終わりに

ここでは complete case analysis を行った 2.1．

さらに時間の対数を取れないような，SwitchOff_Time が 0 のケースを除外した．

この行為の正当性は結構怪しく，元論文 (Horstmann, 2018) での実験計画に戻って正当性を検討する必要があるだろうが，ここではデータ解析のワークフローを見せることを優先してこのような処理を行なった．

また残差の正規性の仮定から大きく離反することが懸念される場合は，ベイズ ANOVA のデフォルト線型モデル解釈は不適になるため，適切な事前分布を設定して一般のサンプラーを用いたベイズ推論を実行する必要があるが，やはり Bayes ANOVA は同じ要領で可能である．

続いてベイズ ANOVA の注意点をここに付しておく．

科学としては，ANOVA と統計的検定はベイズ推論とモデル比較の手続きで代替されるべきであると言える．

しかし，発見を端的に要約したり，伝えるべき聴衆に伝わるためには，「検定」ライクな結果とコミュニケーションは大いに有用である．

ベイズ ANOVA はそのためにベストであるが，上述の目標を達成するための特殊な手続きであり，ベイズデータ分析のワークフローの中に自然な位置を見つけるような解析段階ではないことには注意を要する．

ベイズ ANOVA を実行するためのパッケージには BayesFactor (CRAN / GitHub) がある．BayesFactor では大規模な \(M\)-元配置 ANOVA モデルにおいても Bayes 因子を用いたモデル比較を行うことができる．

一方で bayesanova (CRAN / GitHub) (Kelter, 2022) は，検定ライクな手続きを根本的に排除しており，Gauss 混合モデルとして Gibbs サンプラーによるベイズ推定を実行し，ROPE (Region of Practical Equivalence) (Kruschke, 2018) を用いたベイズ事後分布に基づくモデル比較を行う．

もちろんこのような完全なモデリングを行うことが理想かもしれないが，従来の ANOVA になれきっている研究者にとっては，Bayesian ANOVA に手を伸ばしてみることが次のステップとして大変良いだろう．

5 参考文献

本稿の解析は (van den Bergh et al., 2020) に基づく．

BayesFactor パッケージの使い方は Using the ‘BayesFactor’ package, version 0.9.2+ も参照．

Bayes Anova は階層モデルにおいてどの成分が予測に重要な意味を持つかを定量する極めて強力な手法である．

(Gelman et al., 2014, p. 423) 16.5 節は良い例である．アメリカ合衆国における国民の投票行動をロジットリンクにより二項モデルで一般化線型回帰をしている．Bayes ANOVA により人種による大きな効果と同時に，人種と州の強い交差効果が発見できている．

the analysis of variance is a helpful tool in understanding the importance of diﬀerent components in a hierarchical model. (Gelman et al., 2014, p. 423)

その他の Bayes ANOVA の文献には (Gelman, 2005) などがある．

References

Gelman, A. (2005). Analysis of variance—why it is more important than ever. The Annals of Statistics, 33(1), 1–53.

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014). Bayesian data analysis. Boca Raton : CRC Press.

Horstmann, N. A. L., Aike C. AND Bock. (2018). Do a robot’s social skills and its objection discourage interactants from switching the robot off? PLOS ONE, 13(7), 1–25.

Jakob, L., Garcia-Garzon, E., Jarke, H., and Dablander, F. (2019). The science behind the magic? The relation of the harry potter “sorting hat quiz” to personality and human values. Collabra: Psychology, 5(1), 31.

Kelter, R. (2022). Bayesanova: An r package for bayesian inference in the analysis of variance via markov chain monte carlo in gaussian mixture models. The R Journal, 14, 54–78.

Kruschke, J. K. (2018). Rejecting or accepting parameter values in bayesian estimation. Advances in Methods and Practices in Psychological Science, 1(2), 270–280.

Rouder, J. N., Morey, R. D., Speckman, P. L., and Province, J. M. (2012). Default bayes factors for ANOVA designs. Journal of Mathematical Psychology, 56(5), 356–374.

van den Bergh, D., Doorn, J. van, Marsman, M., Draws, T., Kesteren, E.-J. van, Derks, K., … Wagenmakers, E.-J. (2020). A Tutorial on Conducting and Interpreting a Bayesian ANOVA in JASP. L’Année Psychologique, 120, 73–96.

岡田謙介. (2014). ベイズ統計による情報仮設の評価は分散分析にとって代わるのか?(閉じられたANOVAとその先-心理統計の現状と将来を考える,2013年度日本基礎心理学会第1回フォーラム). 基礎心理学研究, 32(2), 223–231.

永田靖. (2022). 多重比較法の基本的な考え方. 応用統計学, 51(1-2), 31–42.

Footnotes

このような検討は，モデル平均を取ることによってさらに詳細に行うことができる．詳しくは (van den Bergh et al., 2020) も参照．↩︎
ベイズ流に多重比較を行うこともでき，多くの問題を迂回できることが知られている．(岡田謙介, 2014), (van den Bergh et al., 2020) も参照．↩︎

1 はじめに

ベイズデータ解析１

brms によるベイズ混合モデリング入門

ベイズデータ解析５

2 社会的なロボット

2.1 はじめに

2.2 正規性の確認

2.3 （古典的）分散分析の実行

2.4 ベイズ分散分析の実行

2.5 フルモデル係数の事後分布の検討

2.6 ベイズ因子の比較

3 ハリーポッターを用いた性格テスト

3.1 はじめに

3.2 解析の目標

3.3 水準ごとの強度の検討

3.4 まとめ

4 終わりに

5 参考文献

References

Footnotes

`brms` によるベイズ混合モデリング入門