ベイズデータ解析５

回帰モデルの概観

Bayesian
Statistics
Author

司馬博文

Published

12/05/2024

Modified

12/11/2024

概要

ベイズ回帰分析のワークフローを概観する．一つの悲願として，階層モデルを構築して，パラメータをもはや残さず，尤度の推定に成功することがあることを紹介する． 分散分析はこの階層化の際の鍵を握る考え方として，現代でも重要な位置付けを得ることになる． また多くの回帰分析ではデータを変換して線型関係の推定に集中する場合が多く，これを扱う数理モデルとして一般化線型モデルを紹介する．

関連記事

1 回帰分析の一般事項

1.1 はじめに：正規線型回帰

回帰分析とは，２つの確率変数 \(X,Y\) の実現と見られるデータが得られている際に，\(Y\) に対して（より正確にはその条件付き期待値 \(\operatorname{E}[Y|X]\) に対して），\(x\in\mathcal{X}\) に依存する関数としてモデル \[ \mathcal{X}\ni x\mapsto P_{\theta,x}\in\mathcal{P}(\mathcal{Y}) \] を考えることをいう．

例えば \[ P_{\theta,x}=\operatorname{N}(\beta^\top x,\sigma^2),\qquad\theta=(\beta,\sigma), \] とした場合を 正規線型回帰モデル (normal linear model) という．

\(Y\) のモデリングに集中しており，\(X\) には分布の仮定を置いていない点が回帰モデルの特徴である．主に \(X\) を用いた \(Y\) の予測や，\(X\) の \(Y\) への（因果）効果を推定するために用いられる．1

1.2 ベイズ回帰分析

ベイズ回帰分析では，\(Y\) の条件付き構造 \(Y|X\) をモデリングするにあたって，パラメータ \(\theta\) との結合分布 \((Y,\Theta)|X\) をモデリングする．

実際，ベイズ回帰分析では事前分布 \(P_\varphi\) も併せて次の２つのモデルが想定される： \[ Y|(\Theta,X)\sim P_{\theta,x},\qquad \Theta\sim P_\varphi. \] \(\varphi\) はハイパーパラメータとも呼ばれる．

パラメータ \(\theta\) の空間（または \((\theta,\varphi)\) ）上からの確率核 \[ \theta\mapsto P_{\theta,x}(dy)\in\mathcal{P}(\mathcal{Y}) \] を 尤度 という．よく密度 \(p(y|x,\theta)\) の形で表される．

尤度によりデータ \(y\) の空間 \(\mathcal{Y}\) 上の確率分布に関する問題を，パラメータ \(\theta\) の空間上に移送し，事前分布 \(P_\varphi\) からの変化を見ることが （ベイズ）推論 である．

ベイズ回帰分析とは，尤度がパラメータ \(\theta\) の他にデータ \(x\) の関数でもある場合のベイズモデリングに過ぎない．換言すれば，\(Y|X\) の依存構造に焦点がある際に行うベイズ推論である．

1.3 強線型性

仮に２つの説明変数に完全な線型関係がある場合，複数のパラメータ値が同一のモデルを表現するため，パラメータ推定が複数の解を持つ（＝識別不可能）．

この場合 OLS 推定は数値的に不安定になる危険性がある．

一方でベイズ推定は事前分布から与えられる情報によりこのような不安定性が回避でき，多くのデフォルト事前分布はそのように設計されている．(8.4 節 Gelman, Hill, et al., 2020, p. 109) も参照．2

この美点は階層モデリングにおいても引き継がれる．\(J\) 個の指示変数（ダミー変数）を用いた回帰においては，切片項を除けば \(J-1\) 個の指示変数しか追加してはならない．共線型性をもつためである．

しかし階層モデリングにおいては係数に超階層モデルが想定されるため，ここから伝ってくる事前情報が自然に正則化を行い，適切にベイズ推定が行われる (Gelman and Hill, 2006, p. 393)．さらに縮小推定が働き，ほとんどの場合より推定の効率が上がる 2.5．

1.4 ベイズ回帰分析ワークフロー

  1. \((X,Y)\) の依存構造が単純（線型）になるような変数変換を行う（一般化線型モデルの利用を含む）．
  2. \((\Theta,\Phi)\) の事前分布を設定する（初めは一様分布やデフォルトの無情報事前分布で良い）．
  3. 事後分布を計算し，事後予測分布を見てデータが再現できているかを基にモデルを検証する．

その後，十分に階層化をして，パラメータの空間上の事前分布がほとんど情報を持たなくて良いようにする，完全ベイズ推論が一つの悲願とされる．3

モデルの挙動がもはや事前分布に依存しなくなった際，モデルの階層構造や尤度の構造が十分にデータを反映できていると思われるためである．4

推定すべきものはモデルの尤度であってパラメターの値ではないというのが赤池氏の主張です．いいかえると，推定すべきは確率構造であってパラメターではないというのです．(田邉國士, 2010)

この階層化と尤度の推定を探索的に実行できる点がベイズの真の美点だと筆者は考える．そして一度モデルの構造・尤度が明瞭化された際は，もはやベイズである必要はない場合が多い．5

1.5 ベイズ線型回帰からの脱出

前節の立場にたてば，最初の解析は常に（弱い情報を持った事前分布による）ベイズ回帰分析であるべきである．6

これは若干の正則化を加えたロバスト最尤推定に，不確実性の定量化を加えたものと等価であるが，これを MCMC を回すことで一度に実行できる点が美点である．

多くのデフォルト事前分布が開発されており，ほとんど自動的に最初のベイズ回帰分析が実行できる．共線型性が懸念される場合や，小さなデータセットに大きなモデルをフィッティングしようとしている場合などの識別不可能性が生じる状況でも安定した推定値が得られる．

事後分布は豊富な情報を持っており，何より事後予測分布を計算することで予測モデルとしての妥当性を即時に確認できる (PPC: Posterior Predictive Check)．

同時に解析の目標は，適切な関数関係や階層関係を持った階層モデルの発見と，これに適合する（ベイズだろうと点推定だろうと）パラメータ推定法の構成による，ナイーブなベイズ線型回帰からの脱出である．

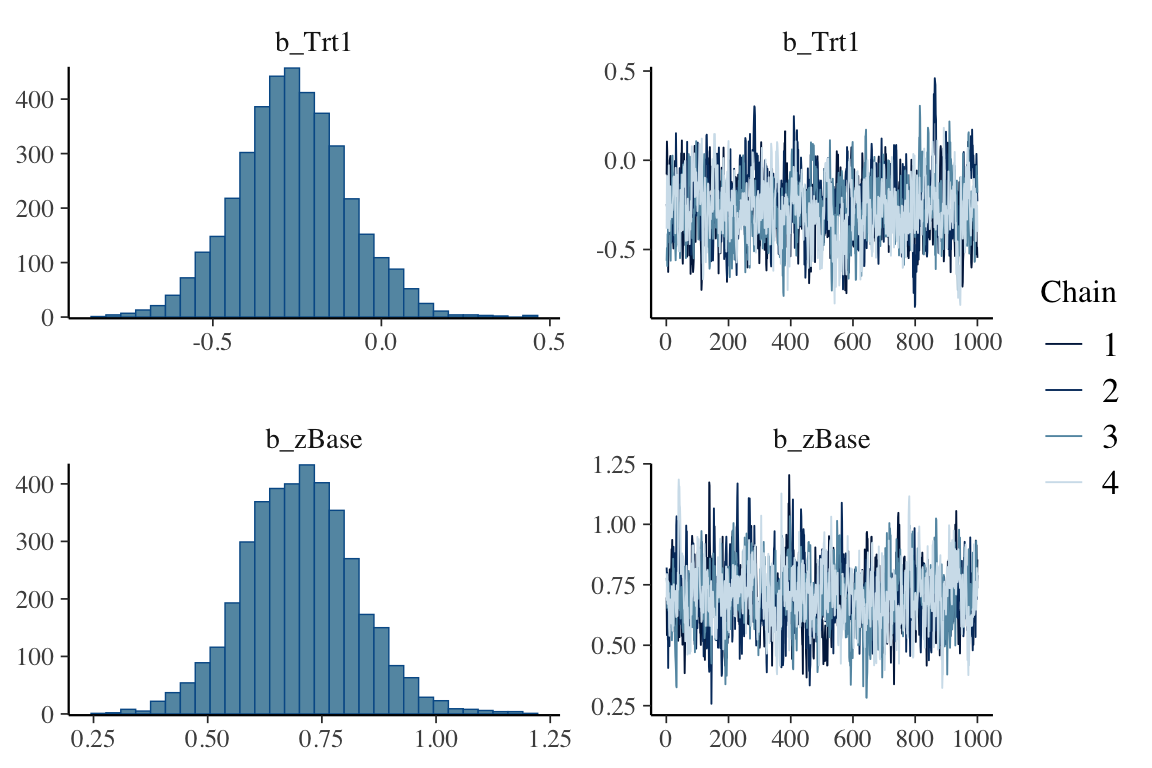
それにあたって，MCMC の収束鈍化も大きな情報である (Bürkner, 2021, p. 32)．

This is the game we (should) play.

2 階層モデル

2.1 はじめに

階層モデルは複雑なモデルを構築するための強力なツールであり，ベイズのワークフローにおいて基本的な要素になる．

層別抽出やクラスター抽出をはじめとして，多くの場合階層別に知識が存在し，これらを系統的に組み込んだ形でモデルを構築できる．

しかし同時に計算が困難になり，第一近似として正規性が仮定される場合が多い．

2.2 混合効果モデル

標本を \(J\) 個のグループにわけ，これへの所属を表す２値変数 \(x_i\in\mathbb{R}^J\) を説明変数に追加するとする．

このような所属変数 \(x_i\) の回帰係数 \(\beta\in\mathbb{R}^J\) に対して階層モデルが考えられる場合が多い．

例えば \(\alpha\in\mathbb{R},\sigma_\beta>0\) をスカラーとして \[ \beta\sim\operatorname{N}_J(\alpha\boldsymbol{1},\sigma^2_\beta I_J), \] という正規モデルを想定した場合，\(x_{ij}\) の係数 \(\beta_j\) は各グループ \(j\in[J]\) 固有の切片項であり，変量効果 (random effect) と呼ばれる．

変量効果の追加は，同一グループ内の \(y_i\) に相関を生じさせるが，グループが違う場合は相変わらず独立のままとする効果がある．

さらに \(\beta_j\) の分散 \(\sigma^2_{\beta_j}\) を \(\infty\) とした場合，すなわち（もはや確率分布ではないが）一様分布を仮定した場合を 固定効果 (fixed effect) という．7

ベイズの立場からは，「変量」と「固定」の名称は歴史的なもので，実質的な違いは「次の階層で回帰モデルを仮定するか，モデルを持たない最終階層の変数と扱い一様事前分布に従うとするか」という仮定の違いにすぎない．詳しくは次節：

この２種の取り扱いをする回帰係数を混在させた場合は 混合モデル (mixed model) という (Gelman et al., 2014, p. 383)．

2.3 階層モデルから見た分散分析

ベイズのワークフローにおいて，複数の説明変数間の階層関係の特定や「どのグループの回帰係数を共通とするか」の見極めが極めて重要である 1.4．

特に，膨大な説明変数の中から「因子」（性別・教育水準・出身地など）とその「水準」（女性・大学院生・山形県民など）とを峻別することが重要であり，どのクラスに独自の回帰係数 \(\beta^{(m)}\sim\operatorname{N}_{J_m}(\alpha_{m}\boldsymbol{1}_{J_m},\sigma^2_{m}I_{J_m})\) を与えるかの決定が，モデルの尤度の改善において大きな効果を持つ (Gelman, 2005)．

\(M\) 元配置の分散分析において，各因子 \(m\in[M]\) に対応する回帰係数は，\(J_m\) 個の水準ごとに次のように決まるバラバラの変動係数を持つとする： \[ \beta^{(m)}_j\sim\operatorname{N}(0,\sigma^2_m),\qquad j\in[J_m]. \] この変量効果としての解釈により，ANOVA は階層モデルの推定とみなせる (3.2節 Gelman, 2005, p. 9)．8

この際の \(\sigma^2_m\) に対する共役（超）事前分布は逆 \(\chi^2\)-分布である (Gelman et al., 2014, p. 396) \[ \sigma^2_{m}\sim\chi^{-2}(\mu_m,\sigma^2_{0m}) \] であり，\(\nu_m=-1,\sigma^2_{0m}=0\) とすることで一様事前分布を得る．

Analysis of variance (Anova) represents a key idea in statistical modeling of complex data structures. (Gelman et al., 2014, p. 395)

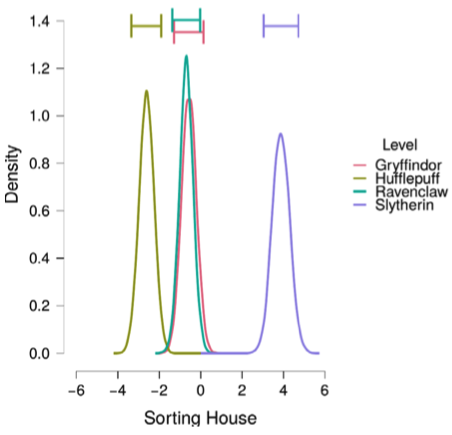
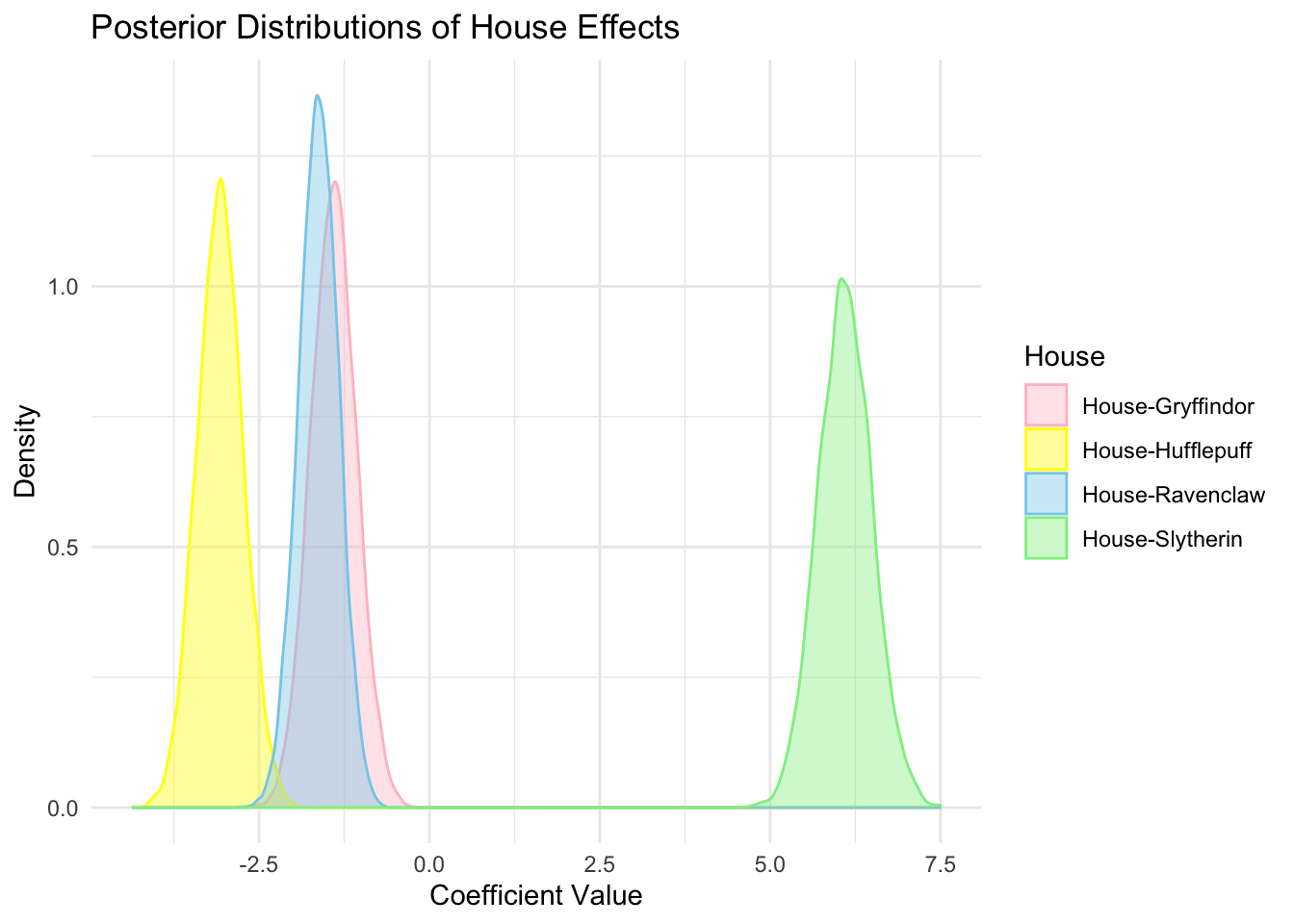
こうして設定された各因子の各水準ごとの係数 \(\beta^{(m)}_j\) の事後分布を見ることで「分散分析」を実行することになる．これがベイズによる分散分析の再解釈である．

2.4 水準ごとの分散

このように分散分析を階層モデルのベイズ推定と再解釈することで，膨大な数の水準の組み合わせに関して，その効果量を定量的に比較することができる．

ここからさらに，\(M\) 個の因子ごとに全ての水準で共通した分散 \(\sigma_1^2,\cdots,\sigma_M^2\) の \(M\) 個のみを考えるのではなく， \[ \beta^{(m)}\sim\operatorname{N}_{J_m}(\alpha_m\boldsymbol{1}_{J_m},\mathrm{diag}(\sigma^2_{m1},\cdots,\sigma^2_{mJ_m})),\qquad m\in[M], \] として，水準ごとにも異なる \(\sum_{m=1}^M J_m\) 個の分散を考えることもできる (15.7 節 Gelman et al., 2014, p. 397)．

この際， \[ \operatorname{Cauchy}(0,A),\qquad A\sim U(\mathbb{R}_+), \] という形の半 Cauchy 分布が \(\sigma^2_{mj}\) の事前分布として用いられる (Gelman et al., 2014, p. 399)．これは一部の水準にのみ大きな分散を認め，その他の水準にはほとんど分散への寄与がないという仮定を表している．

2.5 縮小推定

階層モデルでは，自然に他のグループの情報が共有され，各グループの平均が全体の平均に向けて「縮小」されて推定される．これを (Stein, 1956) から Stein 効果ともいう (Hoff, 2009, p. 146)．9

3 一般化線型モデル

3.1 線型 Gauss 性からの乖離

正規線型モデルから，次の２つの自由度を追加したモデルを 一般化線型モデル (Nelder and Wedderburn, 1972) という：

  1. リンク関数 \(g\)

\[ g\circ\operatorname{E}[Y|X]=\beta^\top X \]

  1. （正規分布以外の）分布族 \(P\)

\[ Y|X\sim P(\operatorname{E}[Y|X],\phi) \]

その結果質的データ解析にも応用可能な広いクラスのモデルを得る．

カウントデータに対する Poisson モデル

自然数値のデータに対して，\(y_i\sim\mathrm{Pois}(\lambda_i)\) の \(\lambda_i\) を，正準リンク関数 \(g=\log\) を通じて \[ \log\lambda_i=X_i^\top\beta \] とモデリングすることが考えられる．このモデルを Poisson 回帰 ともいう．

成功回数データに対する二項モデル

２値データや成功回数を表すデータの場合，\(y_i\sim\mathrm{Bin}(n_i,\mu_i)\) の \(\mu_i\) を \(\operatorname{P}[Y_i=1|X_i]\) の形でモデリングすることを考えることができる．

この場合，正準リンク関数は \[ g(\mu)=\log\frac{\mu}{1-\mu} \] という logit 変換で与えられる．より効率的な推論を促進するために probit リンクや，非対称性を導入する complementary log-log リンク \[ g(\mu)=\log(-\log\mu) \] が用いられることもある (Gelman et al., 2014, p. 407)．

3.2 指数分布族

なお正準リンクとは，Poisson 分布族や二項分布族を指数分布族とみなした際のリンク関数のことである．

例えば二項分布族 \(\{\mathrm{Bin}(n,\mu)\}_{\mu\in(0,1)}\) は，計数測度 \(\nu\) に対して， \[ \frac{d \mathrm{Bin}(n,\mu)}{d \nu}(x)=\begin{pmatrix}n\\x\end{pmatrix}\exp\left(x\log\frac{\mu}{1-\mu}+n\log(1-\mu)\right) \] と表せる．\(g(\mu)\) を 自然な十分統計量 ともいう．

指数分布族と正準リンク関数を用いた一般化線型モデリングは，パラメトリック分布族の十分統計量を代理の応答変数として線型回帰を行なっているものとみなせる．

変換の意味

このような数理統計学的な理由とは別に，\(g(\mu)\) の意味を直接解釈することもできる．

  • Poisson 回帰はオフセット \(\log y_i\) を作ることで， \[ \log\frac{\lambda_i}{y_i}=X_i^\top\beta \] と見ることもできる．\(\lambda_i/y_i\) は観測カウント \(y_i\) に対する平均 \(\lambda_i\) の 率比 (rate ratio) と呼ばれ，\(g(\lambda_i/y_i)\) は対数率比と解釈できる．
  • \(\frac{\mu}{1-\mu}\) という値は成功確率 \(\mu\) に対するオッズ比と呼ばれ，\(g(\mu)\) は 対数オッズ比 (log odds ratio) と呼ばれる．

3.3 分散分析

線型モデルにおいて分散分析は，第一義的には帰無モデルの検定であった．後続の多重比較による解析は，説明変数ごとの効果量の比較を行う．

しかし線型モデルにおいてその方法は分散の分解に基づいており，この一般化線型モデルへの拡張は自明ではない．

一般化線型モデルにおいても残差を定義し，これに基づいてモデルの検証を行うことはできる (Davison and Tsai, 1992)．

4 終わりに

4.1 文献紹介

(Gelman et al., 2014) 第14章で回帰分析，15章で階層モデルが議論されている．15.6, 15.7 章で Bayesian Anova が解説されている．

(Gelman, Hill, et al., 2020) が回帰に特化した本である．

rstanarm パッケージを通じて

library(rstanarm)
fit <- stan_glm(y ~ x, data = mydata)

というコードでベイズ線型回帰を実行できる．family を指定していないため，線型モデルと解釈される．(Muth, 2018) が最適なイントロダクションである．

rstanarm パッケージは特に R の built-in の OLS 推定をする関数

fit <- lm(y ~ x, data = mydata)

や lmer との接続性を意識されているパッケージで，古典的な解析とベイズ分析との往復が容易にできる．

fit <- stan_glm(y ~ x, data = mydata, algorithm = "optimizing")

により変分推論による高速な近似推定も可能である．ベイズ回帰は探索的な用途でも多く使われることを考えると大変有用な機能である．

4.2 「回帰」という名前

回帰分析は従って，\((X,Y)\) の結合分布の形を捉える行為である．

\(X,Y\) の間に不完全な線型関係があり，回帰係数が \(1\) より小さい場合，\(X\) が平均より大きい場合，\(Y\) が平均より大きい確率は小さくなる．

これが「平均への回帰」と呼ばれ，regression の名前の由来となった．

この現象は利用可能性バイアスにより人間に偽の因果関係を簡単に知覚させる (Tversky and Kahneman, 1973)．regression fallacy という名前もついている．

Galton の例では \(X\) が親の身長で \(Y\) が子の身長であった．背の高い両親に恵まれた子供に「残念だね」と声をかける者が居るだろうか？

仮に \(X\) が「褒めたかどうか」で \(Y\) が対象のパフォーマンスであったとするとさらに奇妙なことが起こる．「褒める」ことが激烈に大きな効果を生むわけではない以上，パフォーマンスがよかった場合に褒めると，次にパフォーマンスが落ちる確率が大きくなる．

日常の場面で体感される利用可能な情報がそれだけである以上，これを「褒めると逆効果だ」と知覚しがちなのである．(Kahneman and Tversky, 1973) に素晴らしい例がある．

これゆえ定量的な評価が必要なのである．(6.5 節 Gelman, Hill, et al., 2020, p. 87) も参照．

References

Bafumi, J., and Gelman, A. (2007). Fitting Multilevel Models When Predictors and Group Effects Correlate. SSRN.
Bürkner, P.-C. (2021). Bayesian item response modeling in r with brms and stan. Journal of Statistical Software, 100(5), 1–54.
Davison, A. C., and Tsai, C.-L. (1992). Regression model diagnostics. International Statistical Review / Revue Internationale de Statistique, 60(3), 337–353.
Efron, B., and Morris, C. (1973). Stein’s estimation rule and its competitors–an empirical bayes approach. Journal of the American Statistical Association, 68(341), 117–130.
Efron, B., and Morris, C. (1975). Data analysis using stein’s estimator and its generalizations. Journal of the American Statistical Association, 70(350), 311–319.
Gelman, A. (2005). Analysis of variance—why it is more important than ever. The Annals of Statistics, 33(1), 1–53.
Gelman, A. (2014). How Bayesian Analysis Cracked the Red-State, Blue-State Problem. Statistical Science, 29(1), 26–35.
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014). Bayesian data analysis. Boca Raton : CRC Press.
Gelman, A., and Hill, J. (2006). Data analysis using regression and multilevel/hierarchical models. Cambridge University Press.
Gelman, A., Hill, J., and Vehtari, A. (2020). Regression and other stories. Cambridge University Press.
Gelman, A., Vehtari, A., Simpson, D., Margossian, C. C., Carpenter, B., Yao, Y., … Modrák, M. (2020). Bayesian workflow.
Hoff, P. D. (2009). A first course in bayesian statistical methods. Springer New York.
Kahneman, D., and Tversky, A. (1973). On the psychology of prediction. Psychological Review, 80(4), 237–251.
Muth, Z. A. G., Chelsea AND Oravecz. (2018). User-friendly bayesian regression modeling: A tutorial with rstanarm and shinystan. The Quantitative Methods for Psychology, 14(2), 99–119.
Nelder, J. A., and Wedderburn, R. W. M. (1972). Generalized linear models. Journal of the Royal Statistical Society, Series A (General), 135(3), 370–384.
Stein, C. (1956). Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, 197–206.
Tversky, A., and Kahneman, D. (1973). Availability: A heuristic for judging frequency and probability. Cognitive Psychology, 5(2), 207–232.
久保川達也. (2006). 線形混合モデルと小地域の推定. 応用統計学, 35(3), 139–161.
田邉國士. (2010). 赤池弘次先生を悼む. 応用数理, 20(2), 162–164.

Footnotes

  1. ただし回帰モデルを「因果効果」の推定に用いる際には，通常とは異なる，仮定に対する精査が必要になる．最も安全には，\(x\) が変化した際の \(y\) の変化量を単なる「比較」の文脈で説明することである．この「違い」が \(x\) の変化により生み出されたとは限らないためである．(6.4 節 Gelman, Hill, et al., 2020, p. 85) も参照．↩︎

  2. improper な一様事前分布を用いた場合，引き続き不安定なままな可能性はある．だが多くのデフォルト事前分布は，weakly informative というように，軽微な情報を加えることで正則化が働くように設定されている裾の（適度に）広い事前分布であることが多い．↩︎

  3. 従来は事前分布の経験ベイズ推定と呼ばれていた考え方である (Gelman, Vehtari, et al., 2020, p. 6)．↩︎

  4. 一方で多くの頻度論的な手法は，無情報事前分布を仮定したベイズ推論とみなせる．そこでベイズの，有効な頻度論的モデルを探索するための方法としての美点が見えてくるのである．↩︎

  5. この点については (Gelman, 2014) も参照．大統領選における有権者の行動のモデリングを，ベイズ階層モデルに基づいて探索的に実行しており，“multilevel Bayesian modeling can be considered as an elaborate form of exploratory data analysis” と結論している．↩︎

  6. もちろん重要な事前情報や予備解析が存在する場合は，これを事前分布としてどう更新されるかをみるのが良い．(1.6 節 Gelman, Hill, et al., 2020, p. 16) に簡潔な概観的議論がある．↩︎

  7. (Bafumi and Gelman, 2007) では unmodeled varying intercept と呼んでいる．↩︎

  8. すると「自由度」とは変動係数の数に他ならない．↩︎

  9. 同様の縮小効果を得るための点推定手続きが，経験ベイズ の名称で研究されている (Efron and Morris, 1973), (Efron and Morris, 1975)．これについては (久保川達也, 2006) も参照．↩︎