ベイズデータ解析１

A Blog Entry on Bayesian Computation by an Applied Mathematician

$$

$$

関連記事

1 分散分析

1.1 はじめに

分散分析 (ANOVA: Analysis of Variance) は標本がある因子 \(A,B,\cdots\) によって層別されている場合に，層間の平均効果 \(\mu_i\) に差があるかどうかを検定する手法である： \[ H_0:\mu_1=\cdots=\mu_p\quad\text{v.s.}\quad H_1:\exists_{i,j\in[p]}\;\mu_i\ne\mu_j. \]

因子 \(A,B,\cdots\) の個数に関して，\(A\) のみの場合を一元配置分散分析，\(A,B\) の場合を二元配置分散分析などという．

観測のモデルには 線型 Gauss の仮定が置かれる．例えば一元配置である場合， \[ Y_{ij}=\mu_i+\epsilon_{ij},\qquad i\in[p],j\in[n_i],\epsilon_{ij}\sim\mathrm{N}(0,\sigma^2), \tag{1}\] というモデルが仮定されていることに注意．これは変量効果モデルとも呼ばれる形である．

二元配置では \[ Y_{ij}=\mu+\alpha_i+\beta_j+\epsilon_{ij} \] となり，集団は２つの軸 \(A,B\) で層別されており（分割表の状態），それぞれの因子からの効果 \(\alpha_i,\beta_j\) が説明変数に加法的に加えられる．

1.2 分散分析の抽象的な説明

分散分析では観測 \(Y_{ij}\) の変動のうち，\(H_0\) の仮定の下で説明されなかった部分（残差） \(R_1^2\) と，そもそも線型 Gauss 模型 (1) では説明しきれない部分 \(R_0^2\) とに関して， \[ F:=\frac{(R^2_1-R^2_0)/q}{R^2_0/(n-r)} \] を考える．ただし，\(r:=\operatorname{rank}(X)\) はデータの自由度とした．

この \(F\) は，各群への所属表すダミー変数を用いた回帰分析の残差 \(R_0\) と，各群への所属を考慮しない回帰分析による残差 \(R_1\) とを，自由度を考慮して比を取った形をしている．

この \(F\) は一般に非心 F-分布に従い，仮定 \(H_0\) が成り立つときのみ中心 F-分布 \(\mathrm{F}(q,n-r)\) に従う．

これは各群への所属情報に何の情報量もない場合には，\(F\) が同じ平均を持つ正規確率変数の自乗和の比になるためである．

この \(F\) を検定統計量として仮設検定を実行するのが (repeated measures) ANOVA である．

1.3 Gauss-Markov の仮定

「標本が正規分布に従う母集団からの独立標本である」という帰無仮説を持つ検定に，(Shapiro and Wilk, 1965) の検定などがある．

探索的な方法には Q-Q plot などがある．(Don van den Bergh and Wagenmakers, 2020) も参照．

等分散の仮定をチェックする検定には (Mauchly, 1940) の検定や (Brown and Forsythe, 1974) の検定などがある．

仮にこれらの仮定が破られた場合は，(Kruskal and Wallis, 1952) 検定などのランクベースの ANOVA 手法を用いることができる．¹

ただし，検定はデータの一側面しか伝えていない．例えば，データが帰無仮説をどれほど支持しているかの尺度は検定では得られない．

それゆえ，ANOVA などのモデルの仮定を確認するためには，検定だけでなく他の探索的手法と組み合わせることが推奨される．(Tijmstra, 2018) も参照．

1.4 「検定」に対する注意喚起

一方で ANOVA を含めた検定は一面のみを強調する構造となっており，一連の統計解析の中で自然な位置付けを持つものでない．

特に，\(p\)-値による仮設検定は「データが不十分であることにより判断ができない」ことと，「データと帰無仮説は激しく矛盾する」こととを区別できない．この意味でも限定的な情報量しか持たない．

例えば \(p\)-値が小さく帰無仮説が棄却されたとしても，\(p\)-値はモデルの変化に対して頑健ではないかもしれず，実際はほとんど帰無仮説が成り立つことが真実かもしれない．

このような全貌を探索的に捉えるためには，検定を金科玉条とするのではなく，広くモデル比較・モデル選択の観点からアプローチすることが大切である．同様のことが (Rouder et al., 2016) でも論じられている．

ANOVA は，特に大規模なものが，現在でも実験心理学などの分野で広く用いられている．これは心理学では多くの因子 \(A,B,C,\cdots\) が存在し，それぞれが複雑な関係にあるためである．

しかし推定法も従来の \(F\)-検定を用いたのではその力を十分に発揮できない．解決は丁寧な階層モデリングとベイズによる探索的な解析にある．²

”if you have a complicated data structure and are trying to set up a model, it can help to use multilevel modeling”—not just a simple unitswithin-groups structure but a more general approach with crossed factors where appropriate. This is the way that researchers in psychology use ANOVA, but they are often ill-served by the classical framework of mean squares and F-tests. We hope that our estimation-oriented approach will allow the powerful tools of Bayesian modeling to be used for the applied goals of inference about large numbers of structured parameters. (Gelman, 2005, p. 53)

2 ベイズ分散分析

2.1 はじめに

ベイズ分散分析 (Rouder et al., 2012), (Rouder et al., 2016) では，検定の代わりに Bayes 因子を用いたモデル比較を行う．

特に (Rouder et al., 2012) は標準的な事前分布の選択について議論している．

2.2 考え方

ベイズ的な仮設検定は (Jeffreys, 1961) に源流を持つ．一般に，位置母数の事前分布に Cauchy 分布を用いることは (5.3節 Jeffreys, 1961) に源流を持つ．このことについては (Robert et al., 2009) も参照．

同一の人物を繰り返し測定し， \[ Y_i\overset{\text{iid}}{\sim}\mathrm{N}(\mu,\sigma^2),\qquad i\in[n], \] に従って何らかの処置効果 \(Y_i\) 観測するとし，帰無仮説 \(\mu=0\) の妥当性を議論したいとする．

この際，まずは効果サイズ (effect size) (Cohen, 1988) \(\delta:=\mu/\sigma\) という無次元量にパラメータを変換し，これを Cauchy 分布と比較することを考える： \[ M_0:\delta=0\quad\text{v.s.}\quad M_1:\delta\sim\mathrm{C}(0,1) \]

実際，この Cauchy 分布というのは変換 \(J(\nu,\sigma):=\frac{\mu^2}{\sigma^2}\) を通じて \(\mathbb{R}\) 上の Jeffreys 事前分布（この場合は Lebesgue 測度に一致）に（ほとんど）等価になる．

この２つのモデル \(M_0,M_1\) の残りの仮定は共通の Jeffreys の事前分布 \(p(\sigma^2)\,\propto\,\sigma^{-2}\) で共通とし，Bayes 因子を比較する．

この値を検定統計量のように扱うとき，これを Jeffreys の名前に (Zellner and Siow, 1980) を加えて JZS 因子 (Bayarri and García-Donato, 2007) という．

2.3 \(p\)-値との違い

JZS 因子は \(p\)-値と比較して，サンプルサイズが大きいほど保守的になる傾向がある．(Wetzels et al., 2011) は 2007 年に特定の実験心理学雑誌に投稿された 855 件の t-検定に対して，JZS 因子と \(p\)-値との値を報告してこれを観察している．

(Bergh et al., 2023) は実例を用いて，特に複雑な心理学実験において，２つの解析手法はときに全く違う結論を導くことを例証している．

また JZS 因子は \(N\to\infty\) の極限で，\(\delta\ne0\) であった場合は \(\infty\) に発散し，\(\delta=0\) であった場合は \(1\) に収束するという性質を持つ．

2.4 ANOVA でのベイズ化

１元配置 ANOVA のモデルを次のように表す： \[ \boldsymbol{Y}=\mu\boldsymbol{1}_n+\sigma\boldsymbol{X}\boldsymbol{\theta}+\boldsymbol{\epsilon},\qquad\boldsymbol{\epsilon}|\sigma^2\sim\mathrm{N}(\boldsymbol{0},\sigma^2I_n). \tag{2}\] 各水準 \(i\in[p]\) に属するデータの数を \(n_i\) とすると \[ \boldsymbol{X}=\begin{pmatrix} \boldsymbol{1}_{n_1} & \boldsymbol{0} & \cdots & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{1}_{n_2} & \cdots & \boldsymbol{0}\\ \vdots & \vdots & \ddots & \vdots\\ \boldsymbol{0} & \boldsymbol{0} & \cdots & \boldsymbol{1}_{n_p} \end{pmatrix},\qquad\boldsymbol{\theta}=\begin{pmatrix} \mu_1\\ \mu_2\\ \vdots\\ \mu_p \end{pmatrix}. \] となる．

すると，\(\boldsymbol{\theta}=0\) の場合のモデルが帰無仮説に対応する．

対立仮説としては，\(\boldsymbol{\theta}\) 上に次の \(g\)-prior を定める： \[ \boldsymbol{\theta}\sim\mathrm{N}(\boldsymbol{0},G),\qquad G=\mathrm{diag}(g_1,\cdots,g_p),\qquad g_i\overset{\text{iid}}{\sim}\chi^{-2}(1). \] これは各 \(\mu_i\) に対して独立な Cauchy 事前分布を仮定している．

(Zellner and Siow, 1980) の事前分布 \[ \boldsymbol{\theta}|g\sim\mathrm{N}(\boldsymbol{0},g(\boldsymbol{X}^\top\boldsymbol{X}/n)^{-1}I_p) \] や一般の \(g\)-prior との違いとして，スケール因子 \((\boldsymbol{X}^\top\boldsymbol{X}/n)^{-1}\) がない形であるのは，ANOVA の説明変数 \(\boldsymbol{X}\) が離散変数であるためである．

2.5 ANOVA でのベイズ因子

以上のモデルを，帰無仮説に対立させる「デフォルトモデル」として提案したのが (Rouder et al., 2012) である．

特に \(G=gI_p\) の場合は，結果として得られるベイズ因子は１次元の積分のみを含むため，簡単な数値積分アルゴリズムによって計算可能である．

2.6 多元配置ベイズ ANOVA

ひとまず (Section 8 Rouder et al., 2012) を参照．

2.7 「ベイズ因子」に関する注意喚起

ベイズ因子を含め，周辺尤度 \(p(\theta|y)\) （エビデンスともいう）を用いた指標は，モデルの仮定に対して感度が高い (Robert, 2016), (Kamary et al., 2018)．

そのため「モデルのデータへの当てはまりの良さを１つの指標にまとめた値」としては少し心許ない．

加えて，帰無仮説に対立させる仮説を構成して，二項対立の構造に持ち込むことは，自然なデータ解析のワークフローに必ずしも入ってこない．

ベイズ推論の仮定で得られる事後分布から，特定の仮説 \(H:\theta=\theta_0\) がまともかを評価する方法の方が，探索的データ解析の観点からは含意が多いことも多い．

3 ベイズ推論に基づく方法

3.1 はじめに

ANOVA とベイズ ANOVA の究極的な目標は，平均が一致する \[ H_0:\mu_1=\cdots=\mu_p \] という仮説がデータからどれほど支持されるか／されないかを評価することにある．

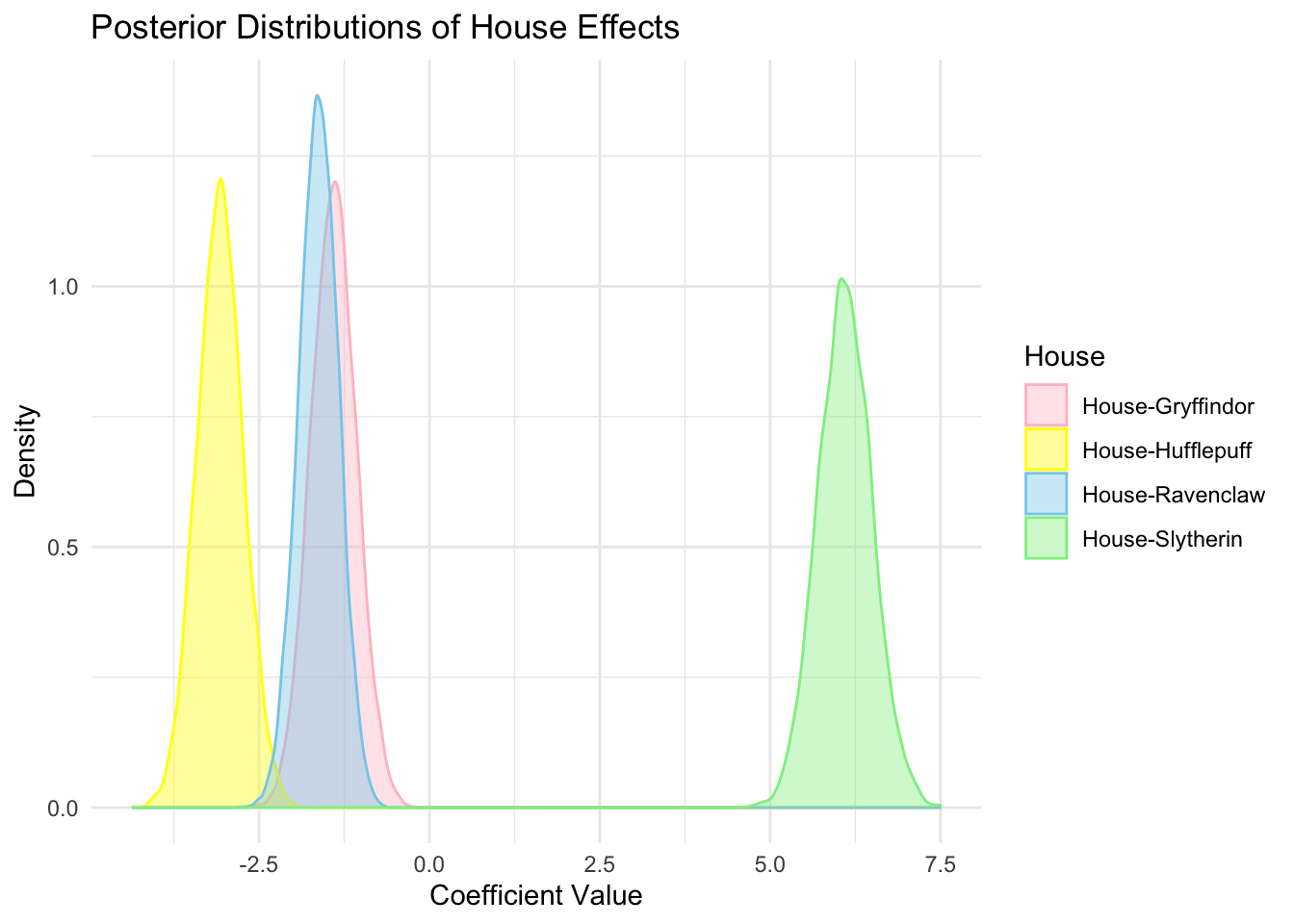
最も直接的な方法は，パラメータ空間上に描かれる事後分布を見ることである．信用区間を報告し，帰無仮説がそのどこに位置するかを見ても良いだろう．

3.2 事後予測によるモデル検証

このように，ベイズ事後分布やそのサンプルを通じたモデル検証方法は posterior predictive check (Gelman and Shalizi, 2013) と呼ばれ，これを多角的に行うことが一つの理想形とされている (Gelman et al., 2020)．

同様に (Kruschke, 2015) では，モデル (2) の形を一般化線型モデルの特別な場合と見て推定し，ANOVA をモデル比較の観点から適切に実行する方法を論じている．

このように，ANOVA を適切に扱うには，階層モデルとしての取り扱いが欠かせない．同様の議論は (Gelman, 2005) でも展開されている．

ここでは，以下の節で帰無仮説 \(H_0\) の妥当性を詳細に評価するための方法を見ていく．

3.3 ベイズ事後 \(p\)-値

Bayes 因子の他に，検定統計量に対するベイズ事後予測分布を導出し，その裾確率を評価して \(p\)-値の代替とする方法もある．

これは 事後予測 \(p\)-値 (posterior predictive \(p\)-value) (Gelman et al., 2014, p. 146) と呼ばれる．

3.4 ROPE (Region of Practical Equivalence)

ROPE は帰無仮説 \(H_0\) と区別がつかないとする区間である．

帰無仮説が \(H_0:\theta=\theta_0\) という形をしていた場合，ほとんどの場合 \(\theta=\theta_0+0.1\) でも事実上変化はない．

このように，帰無仮説と同一視してしまう範囲を ROPE (Kruschke, 2015, p. 336) という．

3.4.1 HDR の使用

この ROPE が 95% 最高密度信用領域 (HDR: Highest Density Region) と互いに素になるときに，「棄却」されたとする．

ただし，最高密度信用領域とは 95% 信用区間＝95% の事後確率を持つ領域のうち，面積が最も小さいもののことを言う．

この方法では，逆に HDR が ROPE を完全に含む場合，帰無仮説を「採択」するという積極的な意思決定も可能である．

ROPE と同様の考え方は，ベイズによる実験計画法でも range of equivalence (Freedman et al., 1984), (Spiegelhalter et al., 1994) の名前で用いられてきた歴史がある．

3.4.2 ROPE の確率

または，事後確率分布が ROPE 内にどれほどの確率を与えるかを見ることもできる (Kruschke, 2018)．

ROPE の応用と実装は (Kelter, 2022) も参照．

3.5 混合モデリングによる方法

ベイズの方法の特徴は，検定・モデル比較と推論とに区別がないことである．

加えて純粋に検定・モデル比較のための手続きを作るより（ベイズ因子など），推定の一種として扱った方がより多くの情報を引き出せるため，ワークフローとしては好ましい (Kruschke, 2011)．

(Robert, 2016), (Kamary et al., 2018) では検定の対象となっているモデル \[ M_1:x\sim f_1(x|\theta_1)\quad\text{v.s.}\quad M_2:x\sim f_2(x|\theta_2) \] を，混合モデル \[ M_\alpha:x\sim\alpha f_1(x|\theta_1)+(1-\alpha)f_2(x|\theta_2) \] の成分の１つとみなし，その荷重 \(\alpha\) の事後分布を推定し，これを検定に用いるという方法が提案されている．

3.6 ハイパーモデル上の推論による解決

同様の発想により，ベイズ因子の計算と推論によるモデル比較とを，より大きなハイパーモデルを立てることで同時に実行することもできる．

(Kruschke, 2011, p. 308) や (O’Neill and Kypraios, 2016) などで考えられている．

4 ベイズ統計解析に関する文献案内

応用分野の研究者に対する「なぜベイズを使うのか？」に対する端的な回答として，「統計的有意性」などの「わかりやすい」指標に飛びついた結果，真のデータの声を聞かずに自分の見たいものを見始めてしまうと言うことが少なく，「自己欺瞞に陥りにくい」という美点があることは，ベイズ機械学習の稿 でも触れた．

\(p\)-値はそのような欺瞞を生む代用例であり，使用を禁止すべきとの声 (Blakeley B. McShane and Tackett, 2019) もある．その論拠は大まかに次のとおりである．

そもそも \(p\)-値とは，「帰無仮説を採用したモデルはデータへの当てはまりの度合いが悪い」ということを言っているだけであり，\(p\)-値が十分に低ければそれ以上の情報は引き出せない．

当然 \(p\)-値が \(0.01\) であることと \(0.00001\) であることは質的に全く変わらない (Gelman et al., 2014, p. 150)．

そのことに加え \(p\)-値は必ずしも頑健な指標ではなく，帰無仮説を少し摂動させただけで \(p\) 値が大きくなってしまうかもしれない．そのような場合は結局ほとんど帰無的であり，「統計的有意性」はほとんど無意味になってしまう．同様の議論が (Gelman and Stern, 2006) で展開されている．

このような現状への対処として，応用分野の研究者にもベイズ統計学は根本的な解決法として広く推奨される (Dienes and Mclatchie, 2018)．(Wagenmakers et al., 2016) はその旨を２つの実例を通じて簡潔に実証しており，同時にベイズ統計学の考え方に対する洗練された導入を行なっている．

(Don van den Bergh and Wagenmakers, 2020) は分散分析をベイズの方法によって実行する手引きを，特に JASP を用いて実演している．

JASP のベイズ ANOVA のエンジンは R パッケージ BayesFactor (CRAN / GitHub) を用いている．BayesFactor では大規模な \(M\)-元配置 ANOVA モデルにおいても Bayes 因子を用いたモデル比較を行うことができる．

ベイズ ANOVA の R パッケージとしては bayesanova (CRAN / GitHub) (Kelter, 2022) もある．これは検定に似た行為を根本的に排除して Gauss 混合モデルとして Gibbs サンプラーによるベイズ推定を実行し，ROPE (Region of Practical Equivalence) (Kruschke, 2015, p. 336) (Kruschke, 2018) を用いたモデル比較を行う．

もちろんこのような完全なモデリングを行うことが理想かもしれないが，従来の ANOVA になれきっている研究者にとっては，Bayesian ANOVA に手を伸ばしてみることが次のステップとして大変良いだろう．

また別の角度からの「ベイズを使うべき理由」としての説得的な議論としては，ベイズ階層モデリングは ANOVA の正統進化という理解 (Gelman, 2005) ができるという向きもある．

以上の立場は (Gelman et al., 2014) や (Kruschke, 2015) などの標準的なベイズデータ解析の教科書でも一貫している．

5 その他の文献案内

F-検定については (吉田朋広, 2006) を参考にした．

ANOVA の歴史については (Tweney, 2014) を参照．(repeated measures) ANOVA は多重線型回帰のうち説明変数が離散変数である場合に相当するという理解は，一般化線型モデルの発展と普及に伴って理解が広がった．

References

Bayarri, M. J., and García-Donato, G. (2007). Extending conventional priors for testing general hypotheses in linear models. Biometrika, 94(1), 135–152.

Bergh, D. van den, Wagenmakers, E.-J., and Aust, F. (2023). Bayesian repeated-measures analysis of variance: An updated methodology implemented in JASP. Advances in Methods and Practices in Psychological Science, 6(2), 25152459231168024.

Blakeley B. McShane, A. G., David Gal, and Tackett, J. L. (2019). Abandon statistical significance. The American Statistician, 73(sup1), 235–245.

Brown, M. B., and Forsythe, A. B. (1974). Robust tests for the equality of variances. Journal of the American Statistical Association, 69(346), 364–367.

Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Routledge.

Dienes, Z., and Mclatchie, N. (2018). Four reasons to prefer bayesian analyses over significance testing. Psychonomic Bulletin & Review, 25(1), 207–218.

Don van den Bergh, M. M., Johnny van Doorn, and Wagenmakers, E.-J. (2020). A Tutorial on Conducting and Interpreting a Bayesian ANOVA in JASP. L’Année Psychologique, 120, 73–96.

Freedman, L. S., Lowe, D., and Macaskill, P. (1984). Stopping rules for clinical trials incorporating clinical opinion. Biometrics, 40(3), 575–586.

Gelman, A. (2005). Analysis of variance—why it is more important than ever. The Annals of Statistics, 33(1), 1–53.

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2014). Bayesian data analysis. Boca Raton : CRC Press.

Gelman, A., and Shalizi, C. R. (2013). Philosophy and the practice of bayesian statistics. British Journal of Mathematical and Statistical Psychology, 66(1), 8–38.

Gelman, A., and Stern, H. (2006). The difference between “significant” and “not significant” is not itself statistically significant. The American Statistician, 60(4), 328–331.

Gelman, A., Vehtari, A., Simpson, D., Margossian, C. C., Carpenter, B., Yao, Y., … Modrák, M. (2020). Bayesian workflow.

Jeffreys, H. (1961). Theory of probability. Oxford University Press.

Kamary, K., Mengersen, K., Robert, C. P., and Rousseau, J. (2018). Testing hypotheses via a mixture estimation model.

Kelter, R. (2022). Bayesanova: An r package for bayesian inference in the analysis of variance via markov chain monte carlo in gaussian mixture models. The R Journal, 14, 54–78.

Kruschke, J. K. (2011). Bayesian assessment of null values via parameter estimation and model comparison. Perspectives on Psychological Science, 6(3), 299–312.

Kruschke, J. K. (2015). Doing bayesian data analysis: A tutorial with r, JAGS, and stan. London ; Tokyo : Academic Press.

Kruschke, J. K. (2018). Rejecting or accepting parameter values in bayesian estimation. Advances in Methods and Practices in Psychological Science, 1(2), 270–280.

Kruskal, W. H., and Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association, 47(260), 583–621.

Mauchly, J. W. (1940). Significance test for sphericity of a normal n-variate distribution. The Annals of Mathematical Statistics, 11(2), 204–209.

O’Neill, P. D., and Kypraios, T. (2016). Bayesian model choice via mixture distributions with application to epidemics and population process models.

Robert, C. P. (2016). The expected demise of the bayes factor. Journal of Mathematical Psychology, 72, 33–37.

Robert, C. P., Chopin, N., and Rousseau, J. (2009). Harold Jeffreys’s Theory of Probability Revisited. Statistical Science, 24(2), 141–172.

Rouder, J. N., Engelhardt, C. R., McCabe, S., and Morey, R. D. (2016). Model comparison in ANOVA. Psychonomic Bulletin & Review, 23(6), 1779–1786.

Rouder, J. N., Morey, R. D., Speckman, P. L., and Province, J. M. (2012). Default bayes factors for ANOVA designs. Journal of Mathematical Psychology, 56(5), 356–374.

Shapiro, S. S., and Wilk, M. B. (1965). An analysis of variance test for normality (complete samples)†. Biometrika, 52(3-4), 591–611.

Spiegelhalter, D. J., Freedman, L. S., and Parmar, M. K. B. (1994). Bayesian approaches to randomized trials. Journal of the Royal Statistical Society: Series A (Statistics in Society), 157(3), 357–387.

Tijmstra, J. (2018). Why checking model assumptions using null hypothesis significance tests does not suffice: A plea for plausibility. Psychonomic Bulletin & Review, 25(2), 548–559.

Tweney, R. D. (2014). History of analysis of variance. In Wiley StatsRef: Statistics reference online. John Wiley & Sons, Ltd.

Wagenmakers, E.-J., Morey, R. D., and Lee, M. D. (2016). Bayesian benefits for the pragmatic researcher. Current Directions in Psychological Science, 25(3), 169–176.

Wetzels, R., Matzke, D., Lee, M. D., Rouder, J. N., Iverson, G. J., and Wagenmakers, E.-J. (2011). Statistical evidence in experimental psychology: An empirical comparison using 855 t tests. Perspectives on Psychological Science, 6(3), 291–298.

Zellner, A., and Siow, A. (1980). Posterior odds ratios for selected regression hypotheses. Trabajos de Estadistica Y de Investigacion Operativa, 31(1), 585–603.

吉田朋広. (2006). 数理統計学,Vol. 21. 朝倉書店.

Footnotes

1. もちろん，Stan などの確率的プログラミング言語を用いた完全なベイズモデリングはいつでも実行可能である．

2. そして因子分析を通じて，記述統計学の正統進化であるということもできる！？ ANOVA の歴史については (Tweney, 2014) も参照．