Sticky PDMP によるベイズ変数選択

非絶対連続分布からの正確なサンプリング

Bayesian
Statistics
PDMP
Author

司馬 博文

Published

12/21/2024

Modified

1/26/2025

1 はじめに

1.1 ベイズ変数選択

ベイズ変数選択には多くの方法がある．次の記事を参照：

本記事ではパラメータ推定とベイズ変数選択を同時に行う方法としては State-of-the-art の１つだと思われる Sticky PDMP によるベイズ変数選択を紹介する．

この方法はパラメータを PDMP によりサンプリングすると同時に，そのダイナミクスを活かすことで，パラメータ選択の離散空間上で非可逆なジャンプを達成する．

1.2 他手法との比較

  1. (3) のような非絶対連続分布からのサンプリングは難しい．そのため spike-and-slab 事前分布 (1) の \(\delta_0\) を分散の小さな正規分布などに軟化した絶対連続な分布に置き換えて，これに対して HMC などの勾配ベースの MCMC 法を適用することもあり得る (Goldman et al., 2022)．
  2. あるいは初めから Laplace 分布や馬蹄事前分布などの絶対連続なスパース誘導事前分布を用い，事後分布は Gibbs サンプラーなどの勾配情報を用いないサンプラーで行う (Griffin and Brown, 2021)，というアプローチもあり得る．

しかし (3) のようなアトムを持った分布に直接適用できる Sticky PDMP によるアプローチは，２の方法と違って非可逆なモデル間ジャンプを達成する効率的なサンプラーである．

さらにその上，Reversible-Jump MCMC の拡張と見れる通り，特定の部分空間にトラップされていた総時間を計算することで，ベイズ因子を計算せずに事後包含確率 (PIP: Posterior Inclusion Probability) を，１の方法と違って誤差なく計算できるという美点がある．

1.3 Sticky PDMP の設定

パラメータ \(x\in\mathbb{R}^d\) 上に spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) \[ p(dx)=\prod_{i=1}^d\biggr(\omega_ip_i(x_i)\,dx_i+(1-\omega_i)\delta_0(dx_i)\biggl) \tag{1}\] を導入して，ベイズ変数選択を行うとしよう．

このとき，モデルの対数尤度を \(\ell(x):=\log p(y|x)\) とすると，事後分布は \[ p(x|y)\,dx\,\propto\,p(y|x)p(dx)=e^{\ell(x)}\prod_{i=1}^d\biggr(\omega_ip_i(x_i)\,dx_i+(1-\omega_i)\delta_0(dx_i)\biggl) \tag{2}\] と表せる．

そこでこの設定を少し抽象化して，ポテンシャル \(\Psi:\mathbb{R}^d\to\mathbb{R}\) を通じて \[ \mu(dx)=Ce^{-\Psi(x)}\prod_{i=1}^d\left(dx_i+\frac{1}{\kappa_i}\delta_0(dx_i)\right) \tag{3}\] と表せる分布 \(\mu\in\mathcal{P}(\mathbb{R}^d)\) からサンプリングする問題を考える．\(\kappa_i\) が小さいほど \(0\) に大きな重みがかかる．

事後分布 (2) は \[ \kappa_i=\frac{\omega_i}{1-\omega_i}p_i(0)(>0) \] と取った場合にあたる．

この \(\mu\) (3) は Lebesgue 測度に関して絶対連続でないため密度を持たず，通常の勾配を用いた MCMC 法を直接は適用できない．

2 Sticky PDMP の理論

2.1 アルゴリズム

The Sticky Zig-Zag Sampler (Bierkens et al., 2023)

  1. 基本的には \[ \mathbb{R}^d\times\{\pm1\}^d \]

    上を動く Zig-Zag サンプラーである．

  2. 任意の座標成分が \(0\) になったとき，すなわち

    \[ \left\{(x,v)\in\mathbb{R}^d\times\{\pm 1\}^d\mid\exists i\in[d]\;x_i=0\right\} \] を通過したとき，該当する座標成分 \(x_i\) は \(0\) に固定される．

  3. 固定された座標 \(x_i\) は，強度 \(\kappa_i\lvert v_i\rvert\) を持つ Poisson 過程が到着するまでそのままである．

これは一見 Markov 過程にならないが，状態空間を拡張して \[ E_0:=\mathbb{R}_{0}^d\times\{\pm1\}^d,\qquad\mathbb{R}_{0}:=(-\infty,0^-]\sqcup[0^+,\infty) \] とし，この上の領域 \[ \partial E_i:=\left\{(x,v)\in E_0\mid (x_i,v_i)=(0^-,-1)\text{ or }(0^+,1)\right\},\qquad i\in[d], \] を吸収的だとすると，この \(E_{0}\) 上の Markov 過程になる．

2.2 設定

\(\partial E_i\) に入った瞬間にその地点から動かなくなり，\(v_i\) は必ずしも「速さ」を表さなくなる，と解する．代わりに \[ \alpha(x,v):=\left\{i\in[d]\mid(x,v)\notin \partial E_i\right\} \] を「アクティブな座標番号」の全体とする．

すると例えば Julia では alpha::Vector{Bool} として，alpha .* v が真の速度ベクトルとなり，簡単に実装できる．これを数式上は \[ v_\alpha:=1_{\alpha(x,v)}\cdot v \] で表すこととする．

続いて \(T_i:\partial E_i\to E_0\) を，\(i\) 番目の座標・速度成分 \((x_i,v_i)\) に関して \[ (0^+,-1)\mapsto(0^-,-1),\qquad(0^-,1)\mapsto(0^+,1) \] と変換する写像とする．

2.3 生成作用素

Zig-Zag サンプラーは各成分ごとに完全に分離したダイナミクスを持つために，生成作用素も \(\widehat{A}=\sum_{i=1}^d\widehat{A}_i\) と表せる．各 \(\widehat{A}_i\) は \[ \widehat{A}_if(x,v)=1_{\partial E_i^\complement}(x,v)\left(v_i\partial_{x_i}f(x,v)+(v_i\partial_{x_i}\Phi(x))_+\biggr(F_i^*f(x,v)-f(x,v)\biggl)\right) \] \[ +1_{\partial E_i}(x,v)\kappa_i\biggr(T_i^*f(x,v)-f(x,v)\biggl). \] と表せ，定義域は \[ \mathcal{D}(\widehat{A})=\left\{f\in L(E_0)\mid f\circ\varphi(-,x,v)\;\text{は絶対連続で}\;\partial E_i\;\text{上にも連続延長する}\right\} \] となる．

2.4 エルゴード性

こうして構成された Zig-Zag サンプラーは，分布 \(\mu\) の裾が重すぎない場合，具体的にはある \(c>d,c'\in\mathbb{R}\) が存在して \[ \Psi(x)>c\log\lvert x\rvert-c',\qquad x\in\mathbb{R}^d, \] を満たすとき（全変動ノルムに関して）エルゴード的である (Prop. A.9 Bierkens et al., 2023, p. 20)．

(\(0\) への再起時刻 Bierkens et al., 2023, p. 6)

\(\mathbb{R}^d\) の原点への再起時刻 \(T_0\) の期待値は \[ \operatorname{E}[T_0]=\frac{1-\mu(\{0\})}{d\kappa\mu(\{0\})}. \]

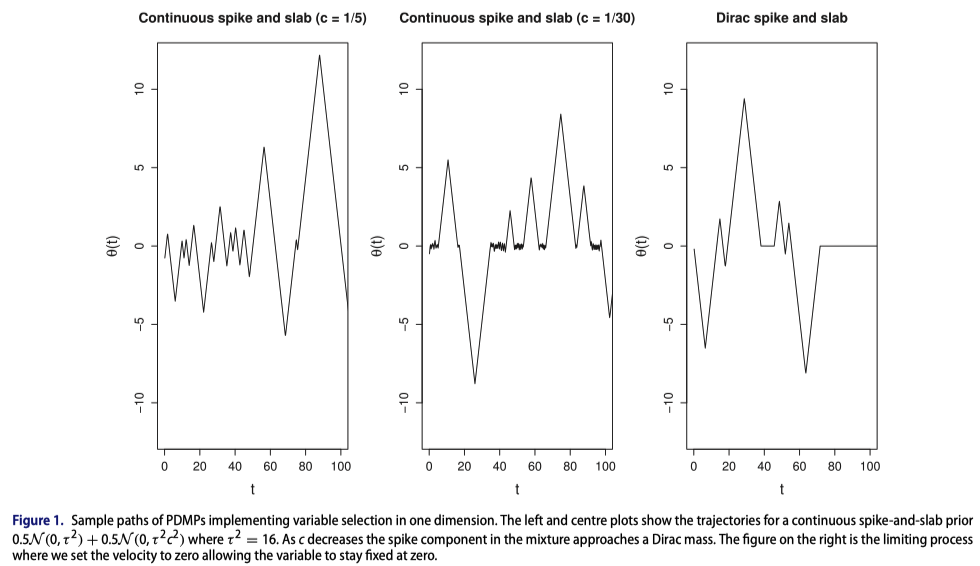
2.5 極限

Sticky Zig-Zag サンプラーは，spike-and-slab 事前分布 (1) を，十分小さい標準偏差 \(c_i>0\) を持つ正規分布で近似した \[ \widetilde{p}(dx)=\sum_{i=1}^d\biggr(\omega_ip_i(x_i)\,dx_1+(1-\omega_i)\mathrm{N}(0,c_i^2)\biggl) \] に対する Zig-Zag サンプラーの，\(c_i\to0\) の極限の場合と見れる (Chevallier et al., 2023, p. 2917)．

(Chevallier et al., 2023, p. 2918)

2.6 一般化

一般に２つの空間 \(E_i,E_j\) の間のジャンプをデザインするとする．

任意に部分集合 \(\Gamma_{i,j}\subset E_i\) を定めて，ここを通過する度に確率 \(p_{i,j}>0\) でジャンプするとすると，ここから戻る Poisson レート \(\beta_{i,j}:E_j\to\mathbb{R}_+\) は \[ \beta_{i,j}(z):=p_{i,j}\frac{}{} \]

3 Sticky PDMP の実装

Sticky Zig-Zag サンプラーは筆者の開発したパッケージ PDMPFlux.jl に実装されている．詳細は次も参照：

4 実装

  • StickyZigZag.jl として実装したが，任意の PDMP サンプラーを受け取って Sticky 化する，というようなコードは書けないか？

References

Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.
Chevallier, A., Fearnhead, P., and Sutton, M. (2023). Reversible jump PDMP samplers for variable selection. Journal of the American Statistical Association, 118(544), 2915–2927.
Goldman, J. V., Sell, T., and Singh, S. S. (2022). Gradient-based markov chain monte carlo for bayesian inference with non-differentiable priors. Journal of the American Statistical Association, 117(540), 2182–2193. doi: 10.1080/01621459.2021.1909600.
Griffin, J. E., and Brown, P. J. (2021). Bayesian global-local shrinkage methods for regularisation in the high dimension linear model. Chemometrics and Intelligent Laboratory Systems, 210, 104255.
Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.