超次元 MCMC

モデル選択のためのマルコフ連鎖モンテカルロ法

Bayesian
MCMC
Statistics
Author

司馬博文

Published

9/22/2024

概要

ベイズ統計におけるモデル選択／モデル平均のためには，異なる次元を持つパラメータ空間を往来するような MCMC サンプラーが必要になる．

Keywords

Reversible Jump MCMC, Sticky PDMP

関連ページ

1 はじめに

1.1 問題設定

本稿では，状態空間が \[ E=\bigcup_{k\in[K]}E_k,\qquad E_k:=\{k\}\times\mathbb{R}^{n_k}, \tag{1}\] により定義される場合を考える．

空間の次元 \(n_k\) は一定とは限らないため，このような状態空間 \(E\) 上に適用される MCMC を 超次元 (trans-dimensional) MCMC と呼ぶ．

このような設定はまずモデル選択において自然に生じる．超次元 MCMC により，モデル（の添え字）の空間 \[ [K]:=\{1,\cdots,K\} \] 上に定まる周辺事後分布を通じて，モデル選択をすることができる．

1.2 例

最初に超次元 MCMC を考えた (Green, 1995) では炭鉱事故データに Poisson モデルを適用し，そのレート関数の変化点解析に応用している．

変化点の存在も数 \(k\in\mathbb{N}\) も不明であるとするとき，\(k\) 個の変化点の位置と，これによって生じる \(k+1\) 個の区間上のレートの値で，モデルの次元 \[ n_k=2k+1 \] が変化する設定が自然に生じる．

続いて２次元の変化点解析として，画像の区分け (segmentation) や物体認識の問題が Voronoi 分割を通じて扱えることが説明されている (Green, 1995, p. 724)．

似た発想として，節点の個数と位置を不定として曲線のフィッティングをする問題にも (Denison et al., 1998) で応用されている．

(Richardson and Green, 1997) では多峰性のある酵素活性データに対して正規混合モデルを適用しており，そのサンプリングに混合比に応じてパラメータ空間の間をジャンプする超次元 MCMC を応用している．

現代では混合数 \(K\) も不定としてデータから学ぶベイズ推定は当然のものとなっているが，初の分析 (Richardson and Green, 1997) は超次元 MCMC の開発 (Green, 1995) を待って初めて可能になったものである．

1.3 滞在時間比によるモデル事後確率の推定

モデル \(k\in[K]\) に関する 周辺尤度 (marginal likelihood) とは，尤度をパラメータ \(\theta\) の事前分布に関して平均をとったもの \[ p(D|k)=\int_{E_k}p(D|k,\theta_k)p(\theta_k|k)\,d\theta_k \] をいう．\(D\) はデータとした．よく \(m_k(D)\) とも表記される．

周辺尤度の比 \[ B_{k',k}:=\frac{p(D|k')}{p(D|k)} \] は Bayes 因子 (Kass and Raftery, 1995) と呼ばれる．

超次元 MCMC によるモデル選択の美点の１つとして，事後モデル確率 \[ p(k|D)\,\propto\,p(D|k)p(k) \] が，MCMC のモデル \(k\in[K]\) への滞在時間の割合によって簡単に計算できることが挙げられる．この方法によるモデル選択は (Carlin and Polson, 1991) などの極めて初期の論文でも提案されている．

ただし，全ての周辺尤度 \(p(D|k)\;k\in[K]\) が得られればベイズ因子も事後モデル確率も計算できるため，これらの値を得るためだけならば必ずしも MCMC による必要はないことに注意する．または MCMC の出力を使ってより効率的に推定することができる (Chib, 1995)．

(Han and Carlin, 2001) は簡便性と得られる情報量とについて，超次元 MCMC と直接周辺尤度を推定する方法とはトレードオフの関係にあるとしている．

2 可逆な方法

2.1 はじめに

本稿ではまず，詳細釣り合い条件を満たすような MCMC のみに焦点を絞って，次元を超える MCMC をどのように構成できるかを議論する．

一般論（第 2.2 節）が (Green, 1995) で議論されている．結局こうして定義されるクラスは，より一般の空間への MH アルゴリズムの拡張となっている：

In brief, reversible jump MCMC is a random sweep Metropolis± Hastings method adapted for general state spaces. (Richardson and Green, 1997, p. 736)

2.2 一般論

目標分布 \(\pi\in\mathcal{P}(E)\) に対して提案核が \[ q(x,-)=\sum_{m=1}^Mq_m(x,-) \] という形で用意されている場合に，棄却率 \(\alpha_m(x,x')\) をどう設定すれば所望の \(\pi\) に収束する Markov 連鎖が得られるかを考える．

(Green, 1995, p. 715)

\(\pi\otimes q_m\) がある \(E^2\) 上の対称な測度に関して密度 \(f_m\) を持つとする．このとき， \[ \alpha_m(x,x')f_m(x,x')=\alpha_m(x',x)f_m(x',x) \] を満たすならば，Metropolis-Hastings サンプラーは \(\pi\) を不変分布にもつ．

(Peskun, 1973) の含意として受容確率はなるべく高い方が良いから，結局は \[ \alpha_m(x,x')=1\land\frac{\pi(dx')q_m(x',dx)}{\pi(dx)q_m(x,dx')}. \] と取ることにあたる．

この命題の前提条件である，「\(\pi\otimes q_m\) がある \(E^2\) 上の対称な測度に関して密度 \(f_m\) を持つ」という条件は dimension-matching requirement と呼ばれる．

仮に \(q_m\) はモデル間のジャンプのみを提案する核であるとする．簡単のために次元は下がるとしよう．その際，ジャンプ先の次元と同じ次元を持った部分多様体上でしか \(q_m\) によるジャンプは起こってはいけないことが要求される．

2.3 ジャンプによる方法

2.3.1 Jump-Diffusion を用いた方法

次元の違う空間をジャンプによって往来するという発想自体は (Grenander and Miller, 1994) が画像認識の分野で提案している．この論文では birth-death の代わりに creation-annihilation と呼ばれている．

ジャンプは Poisson レートに従って起こり，それ以外の間は Langevin 拡散によって平衡分布からのサンプリングを行う．

後にこれを一般のモデル選択に応用したものが (Phillips and Smith, 1995) で議論されており，(Green, 1995) の可逆超次元 MCMC 2.2 の特別な場合に当たる (Green, 1995, p. 716)．

なお，MALA (Metropolis-adjusted Langevin algorithm) はこの論文 (Grenander and Miller, 1994) へのコメント (J. E. Besag, 1994) で提案されたものである．

2.3.2 PDMP への Jump の導入

Jump-Diffusion と全く同様の発想で，PDMP に可逆なジャンプを導入することを提案したのが (Chevallier et al., 2023) である．

ただし (Grenander and Miller, 1994) の提案のように，特定のレートに従ってジャンプをするのではなく，特定の active boundary に到達したら一定の確率でジャンプをするというようにトリガーを決める．

こうすることで超次元ジャンプを起こすために追加の Poisson 過程をシミュレートする必要がなくなり，計算コストが落ちる．(Grenander and Miller, 1994) の方法は，その意味で大変計算コストが高いものだったのである．

そして (Chevallier et al., 2023) の Reversible Jump PDMP では，ジャンプする度に「いつ元のモデルに戻ってくるか」を決める指数到着時間をシミュレートし，それまでの間別のモデルに滞在する，という動きをする．

2.4 混合モデルへの応用

2.4.1 Split-Merge の導入

前述の通り (Richardson and Green, 1997) は混合モデルからのサンプリングに超次元 MCMC を応用している．

ここでは超次元跳躍は，新たな混合成分の導入／削除に用いられる．(Richardson and Green, 1997) は birth-death と呼んでいる．

そして混合成分が追加／削除される前後に，既存の成分の分割／合併 (split-merge) を行うことで，混合モデルからのサンプリングを行う．

この際 (Richardson and Green, 1997) は２次までの積率を変えないように split-merge を行うことを提案しており，これを 積率マッチング (moment matching) ともいう (Fan et al., 2024, p. 10)．

2.4.2 Birth-Death 点過程によるサンプリング

(Stephens, 2000) は混合モデルのパラメータを，複数の \(\Theta\) 上の点を重み付きで足し合わせたものと見ることで，\(\Theta\) 上の事後分布を \(\Theta\) 上の \([0,1]\)-印付き点過程をシミュレーションすることを通じて得られることを示した．

実はこの見方は，第 2.2 節のサンプラーの極限として得られるものである (Cappé et al., 2003)．

同様のメカニズムを，総リスク数不明の競合リスクモデルに PDMP サンプラーと組み合わせて，ベイズモデル平均に適用したのが (Hardcastle et al., 2024) である．

2.5 積空間上の方法

2.5.1 ベイズモデルとしての吸収

超次元 MCMC と同じタイミング (Carlin and Chib, 1995) で，比較したい２つのモデルがあった場合，これらを結合し，足りない specification には “psudo-prior” を設定することで一つの巨大なモデルとみなし，Gibbs サンプラーによって推論するという発想があった．

この考え方は現代もモデル平均につながるが，比較したいモデルが多かったり，\(K\) を無限大にしたい場合は pseudo-prior の設定が煩雑である．

ということでこの方法は必ずしもスケールしないが，超次元 MCMC を包含する広いクラスの手法を特別な場合として含む (Godsill, 2001)．

2.5.2 population-based method

population-based methods の考え方を導入することで，超次元 MCMC の収束を加速することができる．

3 非可逆な方法

3.1 リフティングを用いる方法

リフティングは状態空間を拡張し，MH 法を非可逆にする方法である (Diaconis et al., 2000), (Chen et al., 1999)．

この方法をモデル間のジャンプに応用したものが (Gagnon and Doucet, 2020) で議論されている．

3.2 非可逆なサンプラーを用いる方法

連続時間ベースの MCMC 法は，その非可逆なダイナミクスから従来の MCMC よりも良い収束性を持つ (Andrieu and Livingstone, 2021)．

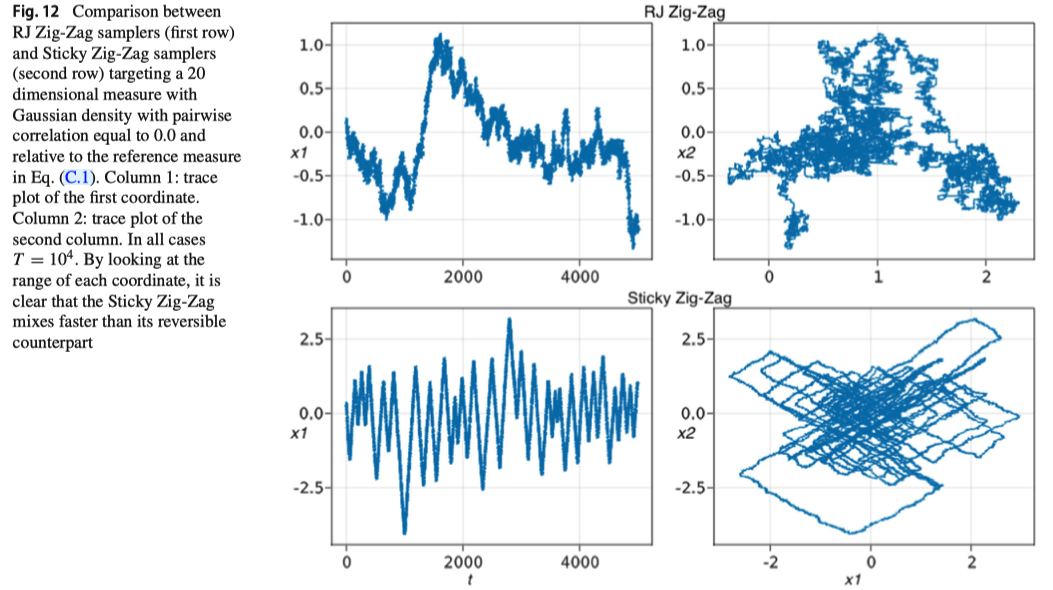
連続時間 MCMC は従来とは全く異なるアルゴリズムをもち，Poisson 過程の到着によりランダムなジャンプをし，それまでは決定論的な動きを続ける（Zig-Zag サンプラーや BPS サンプラーでは直進）．

このようなサンプラーにモデル間の移動を導入するには，新たなタイマー（Poisson 過程）を導入して，その到着のたびにジャンプをすれば良い．

この考え方を推し進めることで，非可逆なモデル間ジャンプをデザインすることができる．

3.3 Sticky PDMP

モデル選択の文脈では，\(E_k\) の間に自然な包含関係がある場合が多い．特に飽和モデルを \(x\in\mathbb{R}^p\) として，この係数に spike-and-slab 事前分布 (Mitchell and Beauchamp, 1988) を仮定して変数選択をする状況を考える： \[ p(dx)=\prod_{i=1}^p\biggr(\omega_ip_i(x_i)\,dx_i+(1-\omega_i)\delta_0(dx_i)\biggl). \]

\(\mathbb{R}^p\) 上でサンプリングを開始し，特定の部分空間に到達する（＝どれかの座標成分が \(0\) になる）たびに，その部分モデルにどれくらいの時間とどまるかを決める「タイマー」を開始し，その間部分空間内のみを探索する，と設計する．

タイマーが鳴った際は止めていた（速度成分を \(0\) にしていた）座標成分を，タイマーが開始された状況と同じ速度で動かし始める．

こうして得られるサンプラーは Sticky PDMP (Bierkens et al., 2023) と呼ばれ，非可逆なサンプラーダイナミクスに依存してタイマーが発動するために，モデル間の非可逆なジャンプを達成することになる．

3.4 境界の導入による方法

モデル選択の文脈では \(E_k\) の間に自然な包含関係があった (nested models) が，合祖木の空間やグラフの空間など，従来から Monte Carlo シミュレーションが困難な離散構造は多く知られている．

そこで一般的な設定を考えたいが，その際に使える Sticky PDMP の一般化のような方法が (Koskela, 2022) で提案されている．

この方法では \(\mathbb{F}\) を一般的な可算集合とし， \[ \mathbb{F}\leftarrow\bigsqcup_{k\in\mathbb{F}}\Omega_m=:\Omega,\qquad\Omega_m\overset{\mathrm{open}}{\subset}\mathbb{R}^d, \] をその上のファイバー束とする．各被覆の境界 \[ \partial\Omega:=\bigsqcup_{k\in\mathbb{F}}\partial\Omega_k \] からサンプラーが出ようとするときに，ある核に従って \(\mathbb{F}\) をジャンプするとするのである．

これにより \(\mathbb{F}\) 上でも非可逆な動きをするサンプラーが，連続変数の空間と離散変数の空間 \(\mathbb{F}\) の合併上で構成できる．

4 文献案内

Trans-dimensional MCMC のトピックは，MCMC の黎明期の歴史に深く関わっている．

(J. Besag and Green, 1993)

Sticky PDMP の間は極めて画期的なアイデアになり，今後数年で PDMP サンプラーをベイズ推論の workhorse algorithm に押し上げるポテンシャルがあるものと筆者は考えている．

実際，連続時間 MCMC アルゴリズムは従来法と大きく違い，収束が多少早い程度ではコミュニティへの浸透が遅いと思われていたが，モデル選択や高次元・多峰性分布への推論に特に優れた応用を見せ始めた今，その重要性が高まっていると言えるだろう．

References

Andrieu, C., and Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: Beyond the reversible scenario. The Annals of Statistics, 49(4), 1958–1981.
Besag, J. E. (1994). Comments on “Representations of Knowledge in Complex Systems” by U. Grenander and M. I. Miller. Journal of the Royal Statistical Society. Series B (Methodological), 56(4), 591–592.
Besag, J., and Green, P. J. (1993). Spatial statistics and bayesian computation. Journal of the Royal Statistical Society: Series B (Methodological), 55(1), 25–37.
Bierkens, J., Grazzi, S., Meulen, F. van der, and Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.
Cappé, O., Robert, C. P., and Rydén, T. (2003). Reversible jump, birth-and-death and more general continuous time markov chain monte carlo samplers. Journal of the Royal Statistical Society Series B: Statistical Methodology, 65(3), 679–700.
Carlin, B. P., and Chib, S. (1995). Bayesian model choice via markov chain monte carlo methods. Journal of the Royal Statistical Society: Series B (Methodological), 57(3), 473–484.
Carlin, B. P., and Polson, N. G. (1991). Inference for nonconjugate bayesian models using the gibbs sampler. The Canadian Journal of Statistics / La Revue Canadienne de Statistique, 19(4), 399–405.
Chen, F., Lovász, L., and Pak, I. (1999). Lifting markov chains to speed up mixing. In Proceedings of the thirty-first annual ACM symposium on theory of computing, pages 275–281. New York, NY, USA: Association for Computing Machinery.
Chevallier, A., Fearnhead, P., and Sutton, M. (2023). Reversible jump PDMP samplers for variable selection. Journal of the American Statistical Association, 118(544), 2915–2927.
Chib, S. (1995). Marginal likelihood from the gibbs output. Journal of the American Statistical Association, 90(432), 1313–1321. doi: 10.1080/01621459.1995.10476635.
Denison, D. G. T., Mallick, B. K., and Smith, A. F. M. (1998). Automatic bayesian curve fitting. Journal of the Royal Statistical Society. Series B (Statistical Methodology), 60(2), 333–350.
Diaconis, P., Holmes, S., and Neal, R. M. (2000). Analysis of a nonreversible markov chain sampler. The Annals of Applied Probability, 10(3), 726–752.
Fan, Y., Sisson, S. A., and Davies, L. (2024). Reversible jump markov chain monte carlo and multi-model samplers.
Gagnon, P., and Doucet, A. (2020). Nonreversible jump algorithms for bayesian nested model selection. Journal of Computational and Graphical Statistics, 30(2), 312–323. doi: 10.1080/10618600.2020.1826955.
Godsill, S. J. (2001). On the relationship between markov chain monte carlo methods for model uncertainty. Journal of Computational and Graphical Statistics, 10(2), 230–248. doi: 10.1198/10618600152627924.
Green, P. J. (1995). Reversible jump markov chain monte carlo computation and bayesian model determination. Biometrika, 82(4), 711–732.
Grenander, U., and Miller, M. I. (1994). Representations of knowledge in complex systems. Journal of the Royal Statistical Society. Series B (Methodological), 56(4), 549–603.
Han, C., and Carlin, B. P. (2001). Markov chain monte carlo methods for computing bayes factors. Journal of the American Statistical Association, 96(455), 1122–1132. doi: 10.1198/016214501753208780.
Hardcastle, L., Livingstone, S., and Baio, G. (2024). Averaging polyhazard models using piecewise deterministic monte carlo with applications to data with long-term survivors.
Kass, R. E., and Raftery, A. E. (1995). Bayes factors. Journal of the American Statistical Association, 90(430), 773–795. doi: 10.1080/01621459.1995.10476572.
Koskela, J. (2022). Zig-zag sampling for discrete structures and nonreversible phylogenetic MCMC. Journal of Computational and Graphical Statistics, 31(3), 684–694. doi: 10.1080/10618600.2022.2032722.
Mitchell, T. J., and Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.
Peskun, P. H. (1973). Optimum monte-carlo sampling using markov chains. Biometrika, 60(3), 607–612.
Phillips, D. B., and Smith, A. F. M. (1995). Markov chain monte carlo in practice. In W. R. Gilks, S. Richardson, and D. Spiegelhalter, editors, pages 215–240. Chapman; Hall/CRC.
Richardson, Sylvia., and Green, P. J. (1997). On bayesian analysis of mixtures with an unknown number of components (with discussion). Journal of the Royal Statistical Society: Series B (Statistical Methodology), 59(4), 731–792.
Stephens, M. (2000). Bayesian analysis of mixture models with an unknown number of components—an alternative to reversible jump methods. The Annals of Statistics, 28(1), 40–74.