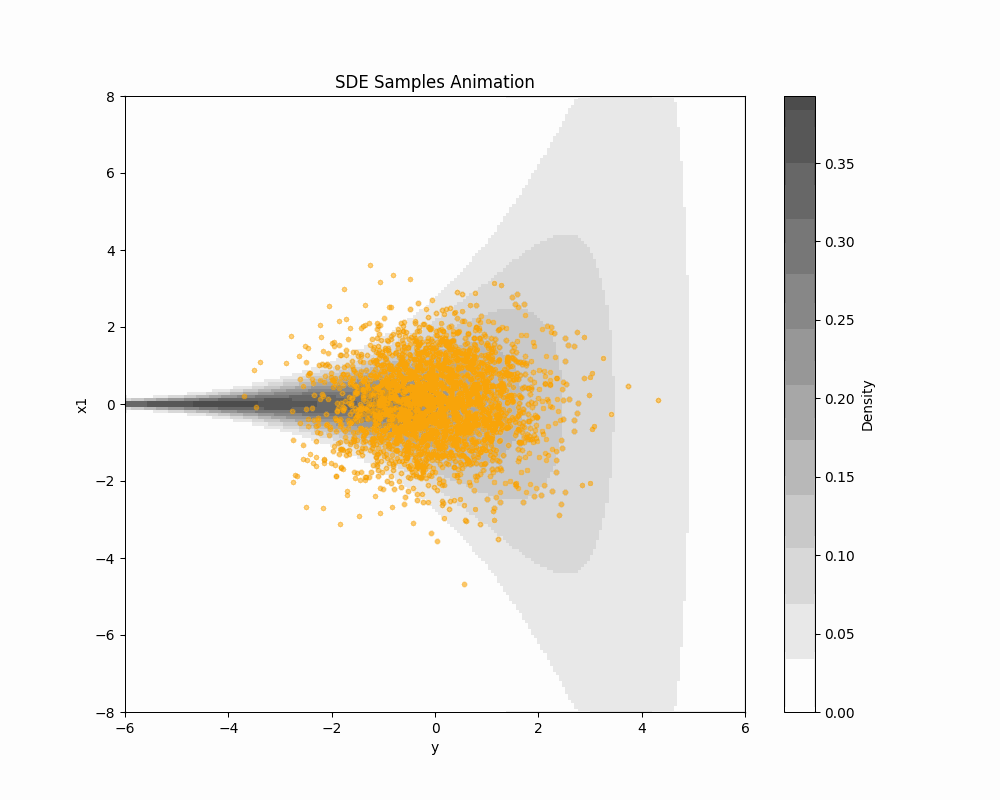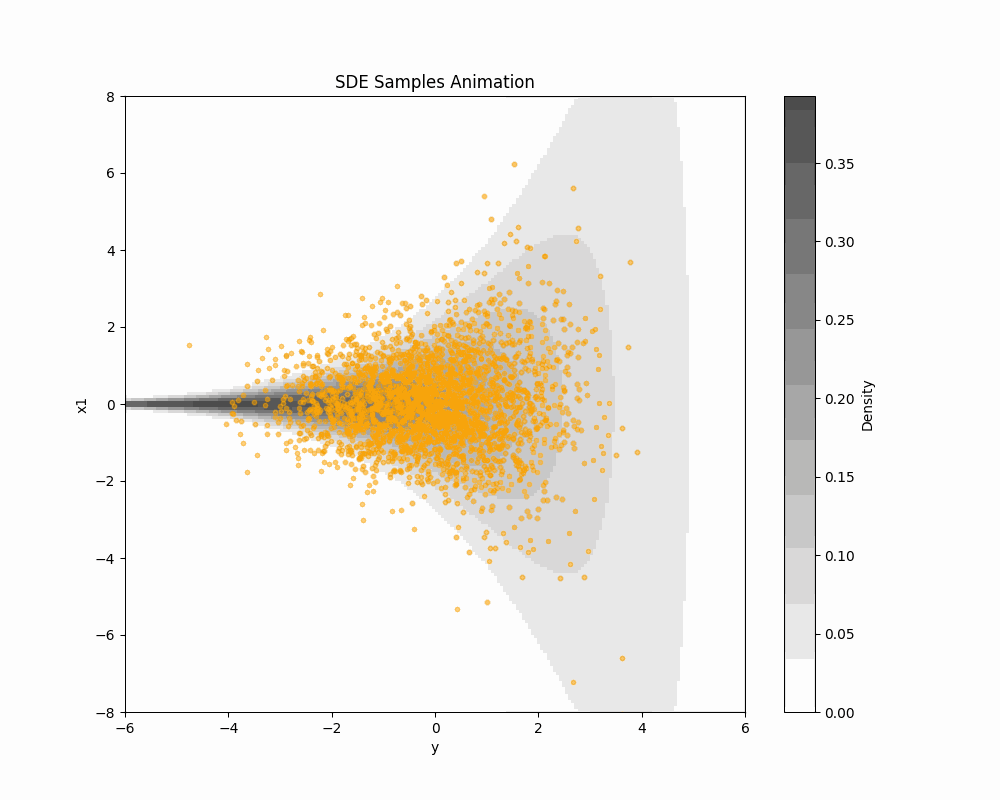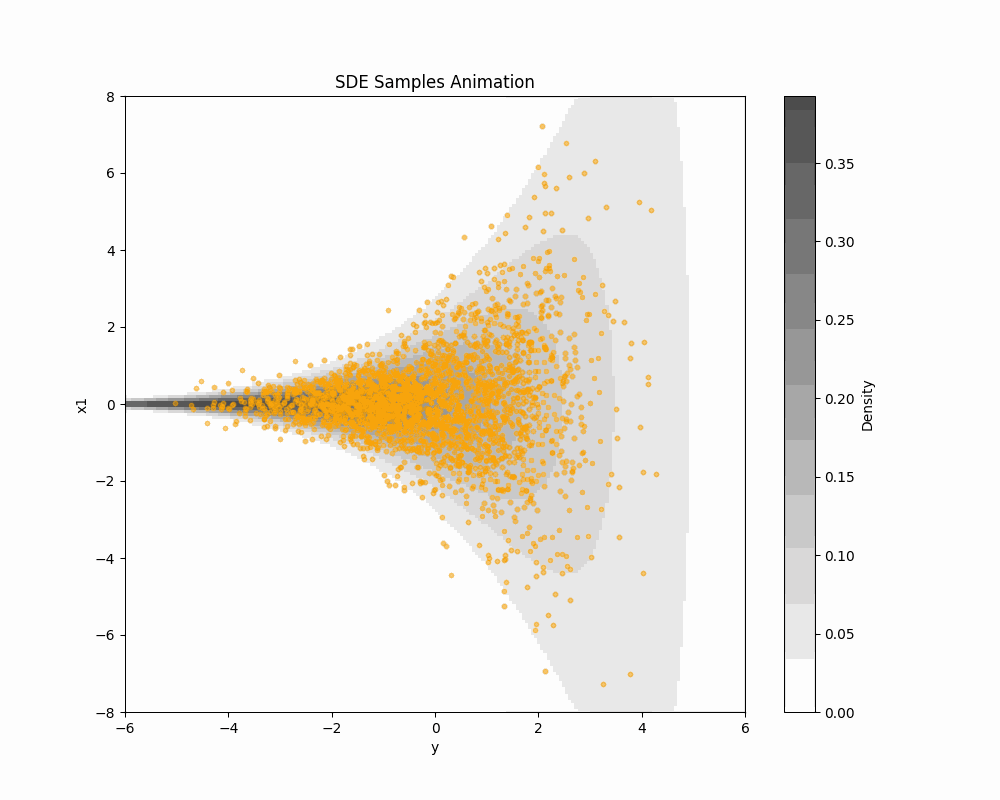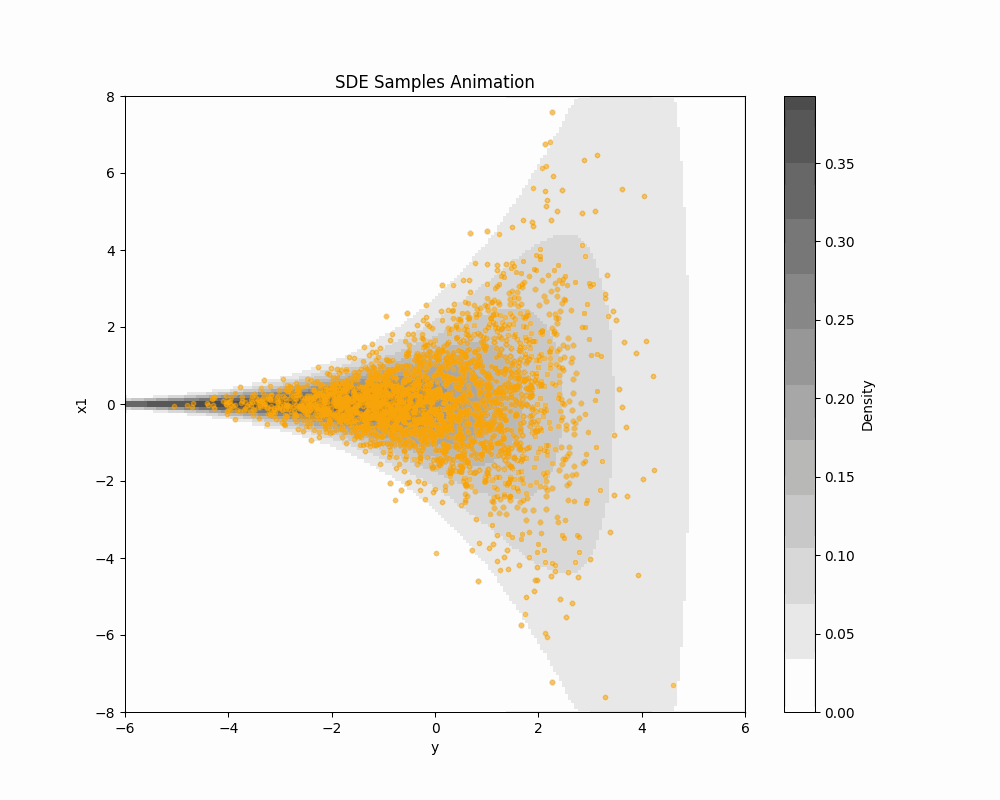
輸送手法一覧
A Blog Entry on Bayesian Computation by an Applied Mathematician
$$
$$
1 アイデア
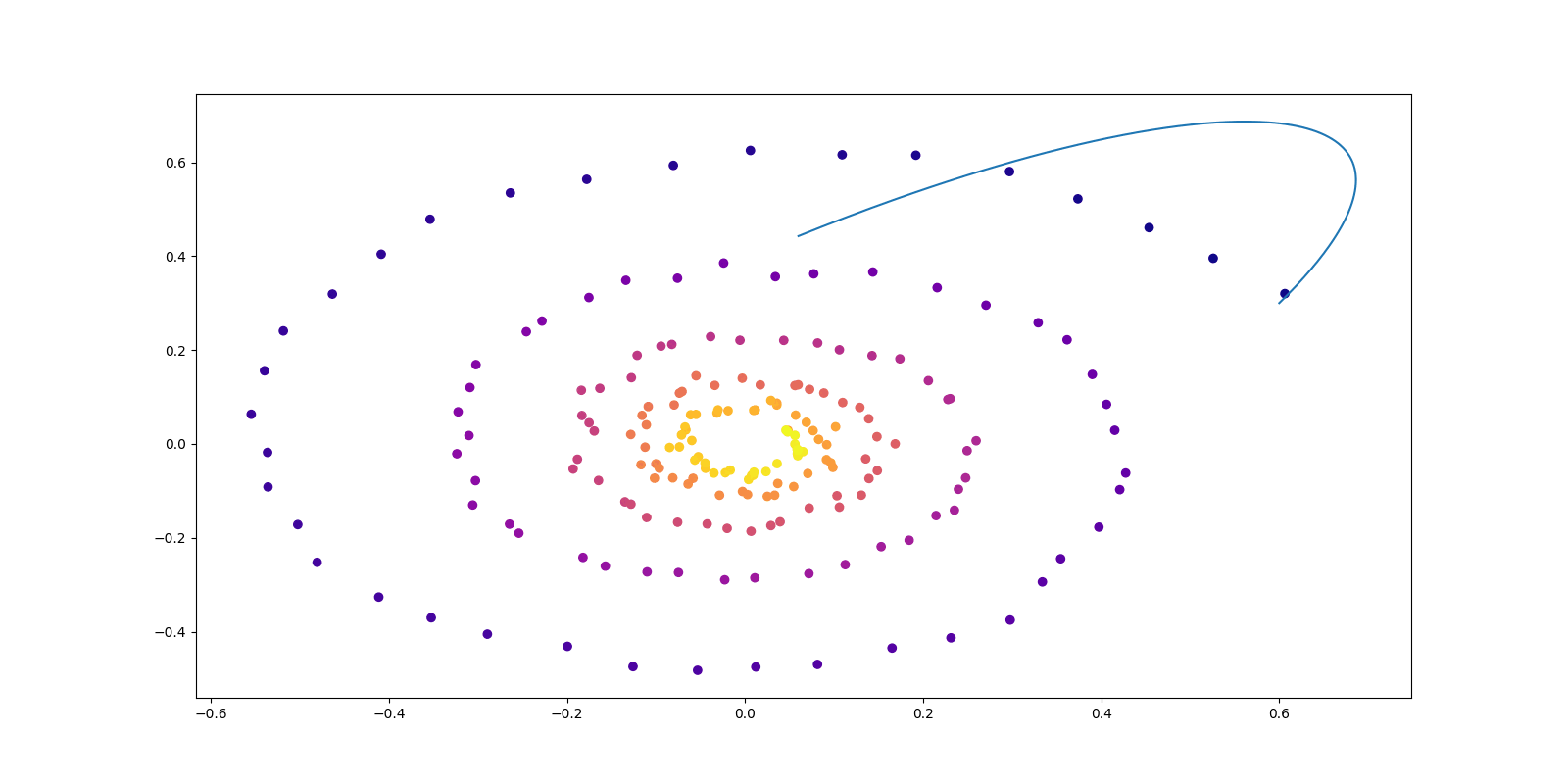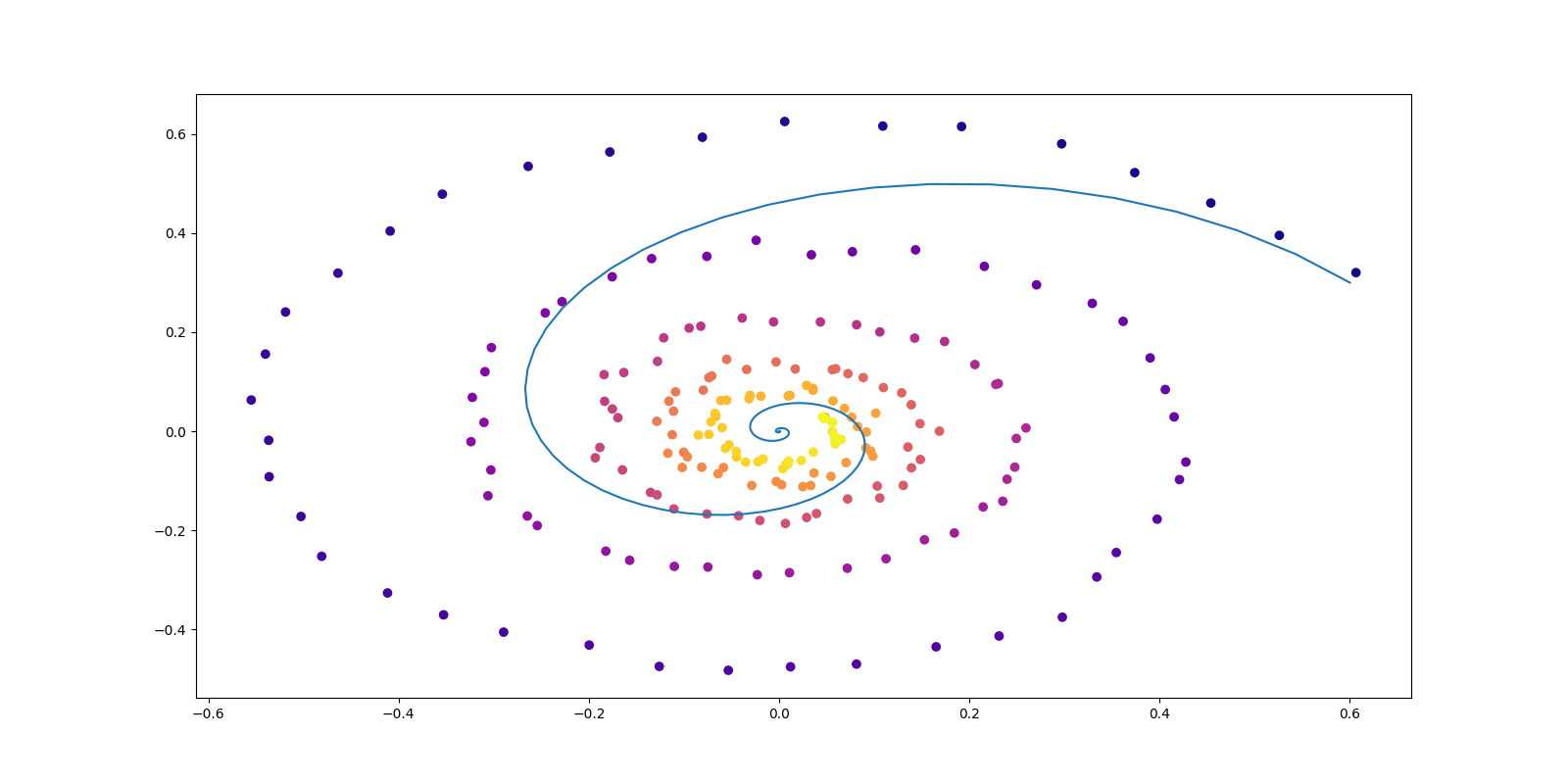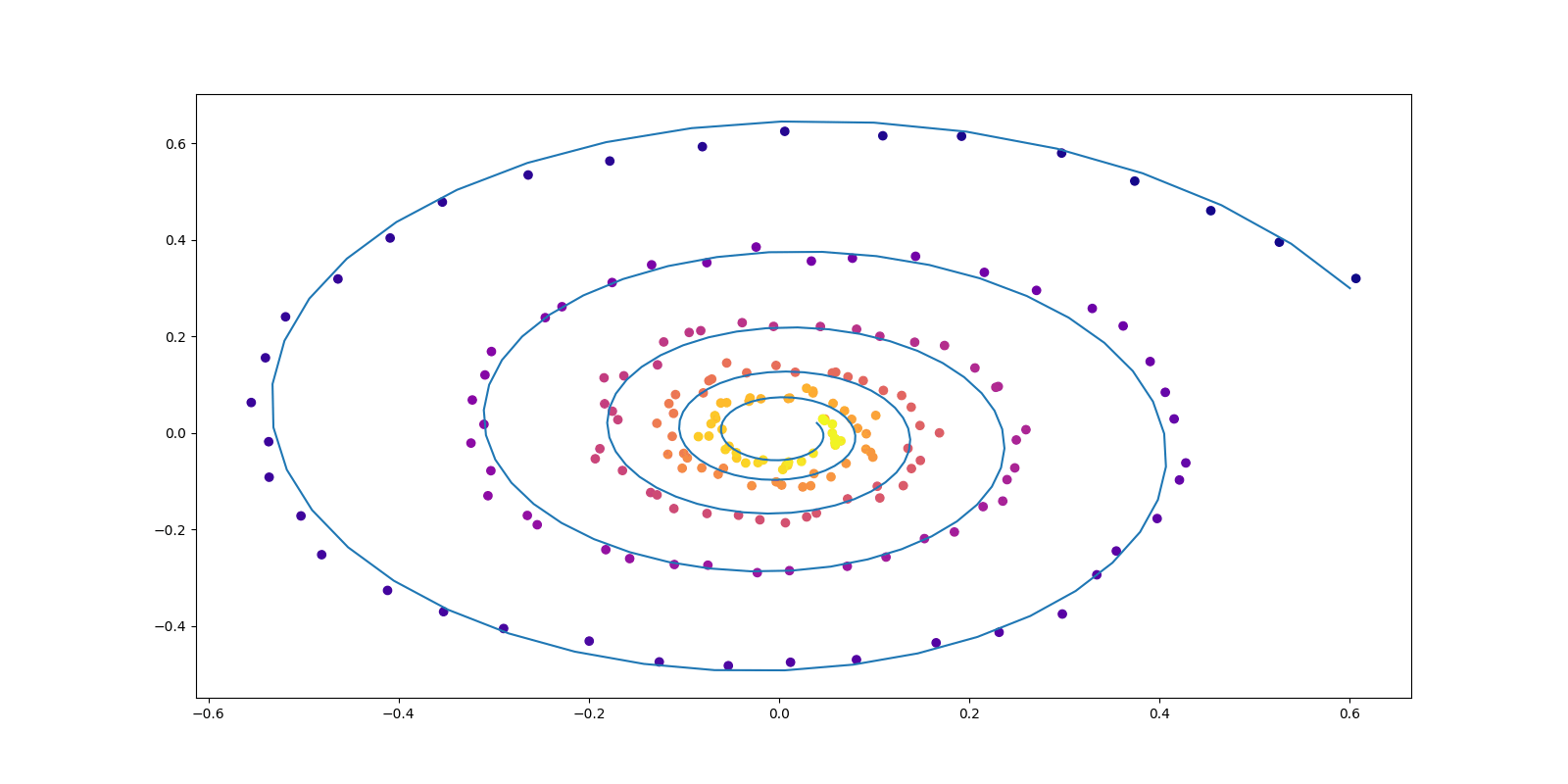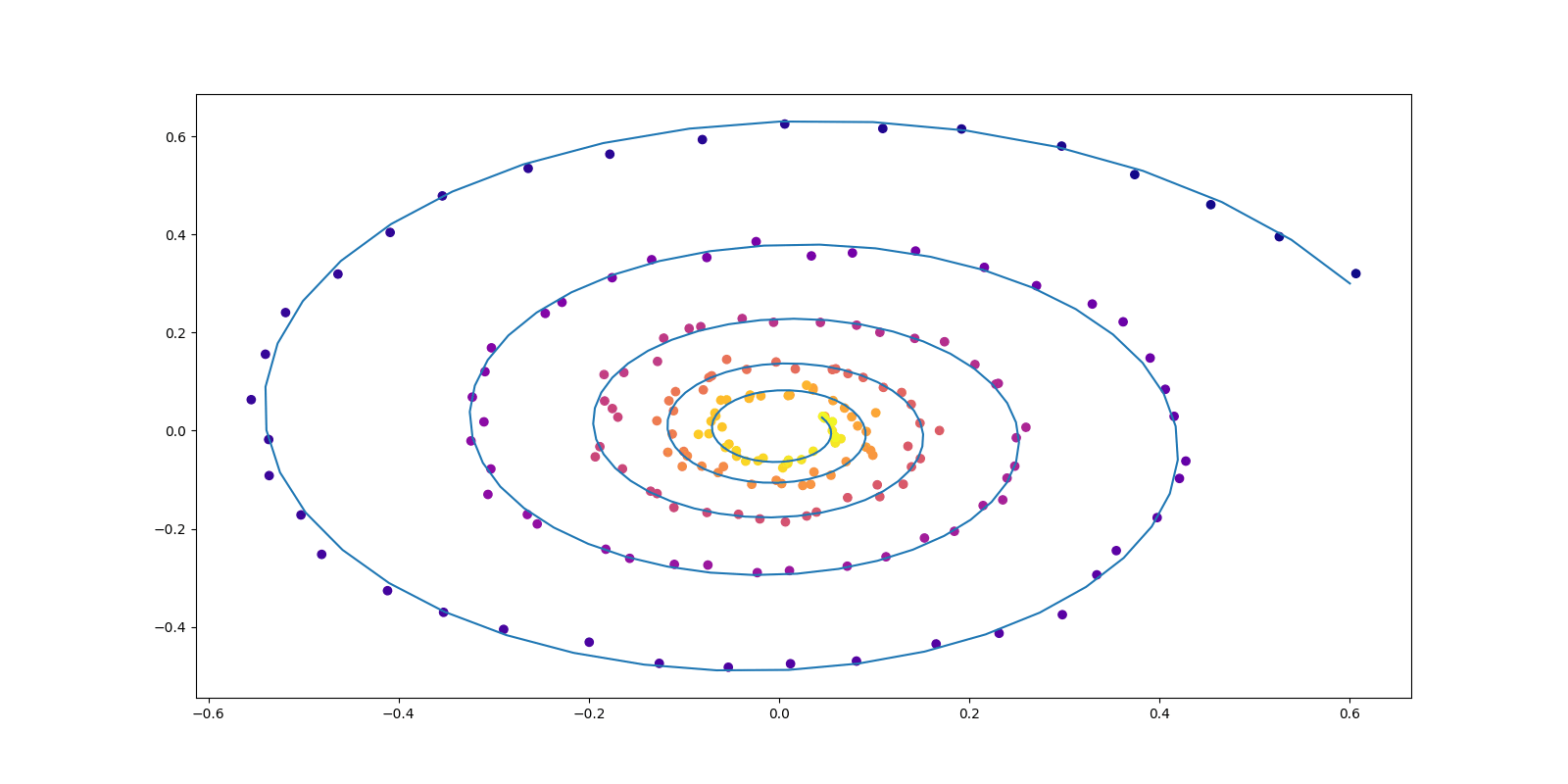
1.1 輸送問題としての生成モデリング
生成モデリングの悲願は,2つの分布 \(P_0,P_1\in\mathcal{P}(\mathbb{R}^d)\) を結ぶ輸送写像 \(\phi:\mathbb{R}^d\to\mathbb{R}^d\) \[ \phi_*P_0=P_1 \] を,\(P_0,P_1\) が定める PDE のフロー \((\phi_t)\) を学習することで \(\phi:=\phi_1\) として得ることにある.
この夢は現在,連続時間の正規化フロー,フローマッチング,確率的補間,Rectified Flow などの名前で追及されている:
1.2 ベクトル場を学習する Flow Matching
このようなフロー \((\phi_t)\) を定めるベクトル場 \(F_t\) \[ \frac{\partial \phi_t(x)}{\partial t}=F_t(\phi_t(x)) \] は,\(P_0,P_1\) を補間する確率密度 \[ P_t:=(\phi_t)_*P_0 \] の密度 \(p_t\) に対して,連続方程式 というPDE \[ \frac{\partial p_t}{\partial t}+\operatorname{div}(F_tp_t)=0. \] を満たす必要がある.
この PDE を満たす適切なベクトル場 \(F_t\) を特定し,これを目的にニューラルネット・ベクトル場 \(F_\theta(x_t,t)\) を学習してサンプリングに活かすことが,FM (Flow Matching) により可能になる.
1.3 歴史:拡散モデル
決定論的なフロー \((\phi_t)\) による \(P_0\) の \(P_1\) への変換が考えられる前は,確率的に \(P_0\) を \(P_1\) に変換する方法が 拡散モデル (DDPM / SGM) という名前で考えられていた.
この方法では \(P_1\) から開始して \(P_0\) に収束するエルゴード性を持つ OU 過程の時間反転・拡散除去過程 (DD: Denoising Diffusion) を学習することで,ノイズ分布 \(P_0\) からのサンプルをデータ分布 \(P_1\) からのサンプルに変換するダイナミクスの獲得を目指す.
DDPM (Denoising Diffusion Probabilistic Model) (Ho et al., 2020) は確率モデルとしてこの枠組みを定式化しパラメータの最尤推定を目指した.SGM (Score-based Generative Model) (Song et al., 2019) はデータ分布のスコア \(\nabla_x\log p_t(x)\) をスコアマッチングにより学習することでドリフト項を直接推定する方法を提案した.
これらの方法にはノイズスケジュールなどの不要なパラメータや調節可能なハイパーパラメータが多く,等価な分布変換を定める ODE が存在する (Song et al., 2021) ことが自覚されると,ODE とベクトル場による方法が志向された.これで Flow Matching (Lipman et al., 2023) に至る.
しかし DD のように確率過程の時間反転を用いる方法は,離散空間や Riemann 多様体などの極めて一般的な状態空間 \(\mathcal{X}\) に適用可能であるという強みも持つ (Benton et al., 2024).詳しくは次の稿で扱う:
1.4 Schrödinger 橋
分布 \(P_1\) から開始する OU 過程は,エルゴード性をもてど有限時間内で \(P_0\) との誤差が消えるわけではない.実際,拡散モデルの時間極限 \(T>0\) はなるべく大きく取ることが推奨されている (Song and Ermon, 2020).つまり,\(P_0,P_1\) を補間するダイナミクスとしては近似的なものでしかない.
一方で,正確に2つの分布 \(P_0,P_1\) を繋ぐダイナミクスの1つを Schrödinger 橋 (SB: Schrödinger Bridge) (Schrödinger, 1931), (Schrödinger, 1932) が与える.1
SB は DD を初期値とした IPF (Iterative Proportional Fitting) / Sinkhorn-Knopp アルゴリズムを通じて計算でき,SB により正確で高速な条件付き生成/事後分布サンプリングが可能になることを (Shi et al., 2022) が最初に指摘した.
SB をスコアマッチングによって学習することが (Heng et al., 2022) によって考えられた.
1.5 サンプリングに向けて
ここまでの議論では,両端の確率分布 \(P_0,P_1\in\mathcal{P}(\mathbb{R}^d)\) が正確に定まっており,自由にサンプルを得ることが可能だと仮定してきた.
統計学でよく見られる状況は,\(P_0,P_1\) の正規化定数が未知であるという状況である.
たったこれだけで問題は一気に難しくなる.
事後分布サンプリングだけでなく,一般の正規化定数が不明な分布 \[ \pi(x)=\frac{\gamma(x)}{Z},\qquad Z:=\int_\mathcal{X}\gamma(x)\,dx \] に対するサンプリング手法 雑音除去サンプラー (DDS: Denoising Diffusion Sampler) (Vargas et al., 2023) が提案された.
DDS では \(\nabla\log p_{T-t}\) の推定を \(h\)-変換により回避し,スコアマッチングの代わりに KL 最適制御問題を解くことでドリフト項を推定する.
1.6 SB による輸送サンプラー
同様のサンプラーの高階化
1.7 まとめ
以上の発展は次のようにまとめることもできる (Heng et al., 2024):
| 名称 | 正規化定数の不明な分布に使えるか? | IPF が必要か? |
|---|---|---|
| DD による条件付き生成 (Ho et al., 2020), (Song et al., 2019) | ||
| SB による条件付き生成 (Shi et al., 2022) | ||
| DD によるサンプリング(DDS) (Vargas et al., 2023) | ||
| SB によるサンプリング (Heng et al., 2024) |
References
Footnotes
(Schrödinger, 1931) の英訳が (Chetrite et al., 2021) により与えられている.↩︎