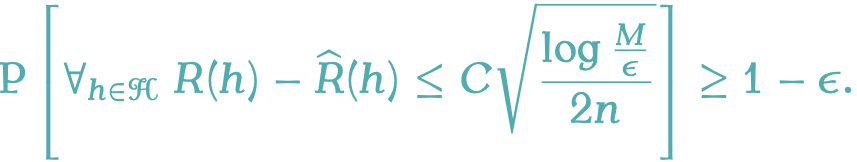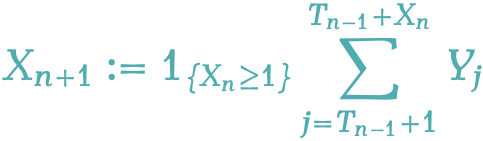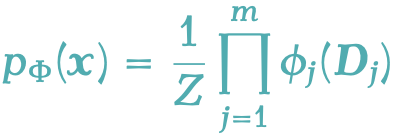Masked Diffusion Models
MCMC と PDMP の概観
セミパラメトリック重回帰分析
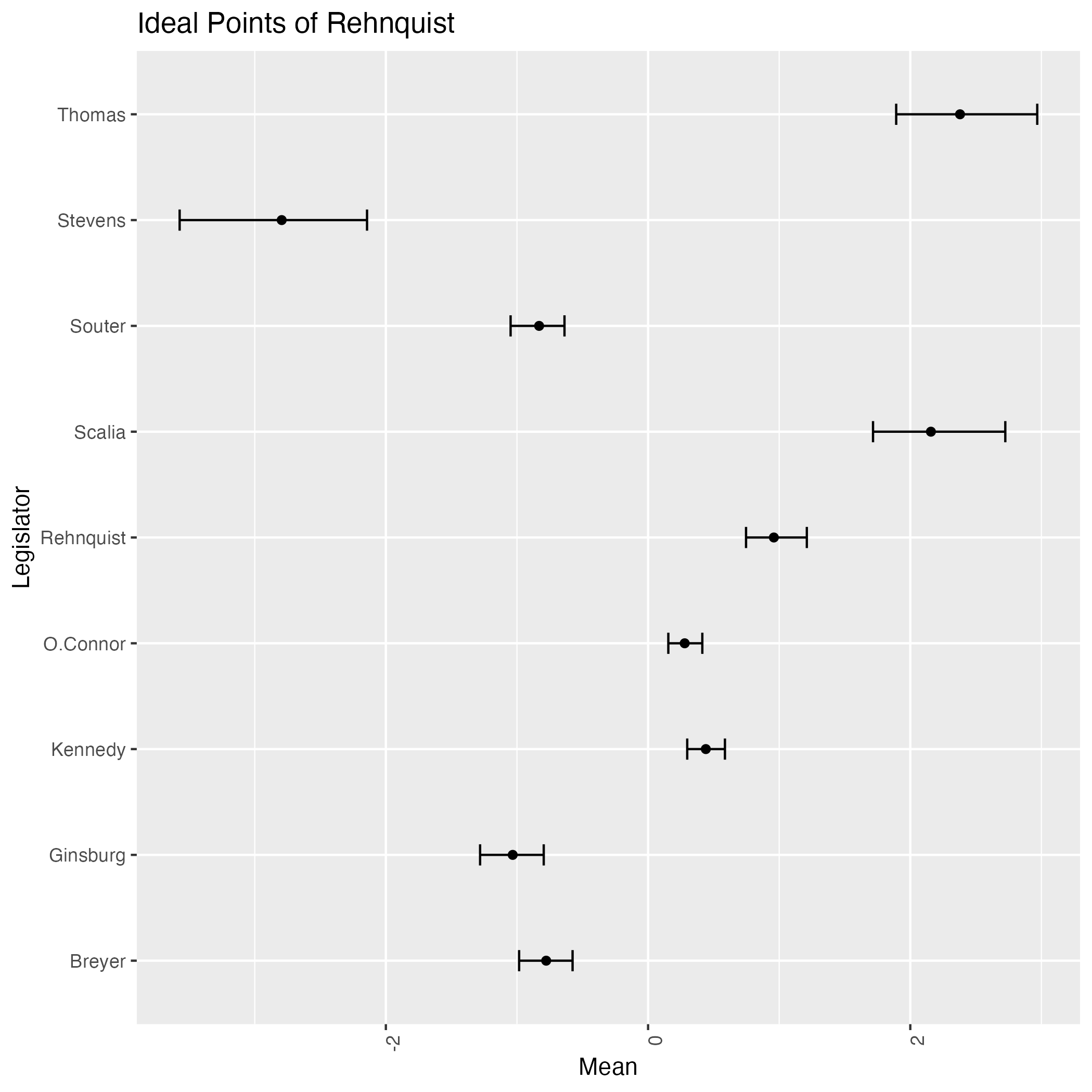
On the Identifiability of the Bafumi et. al. Ideal Point Model
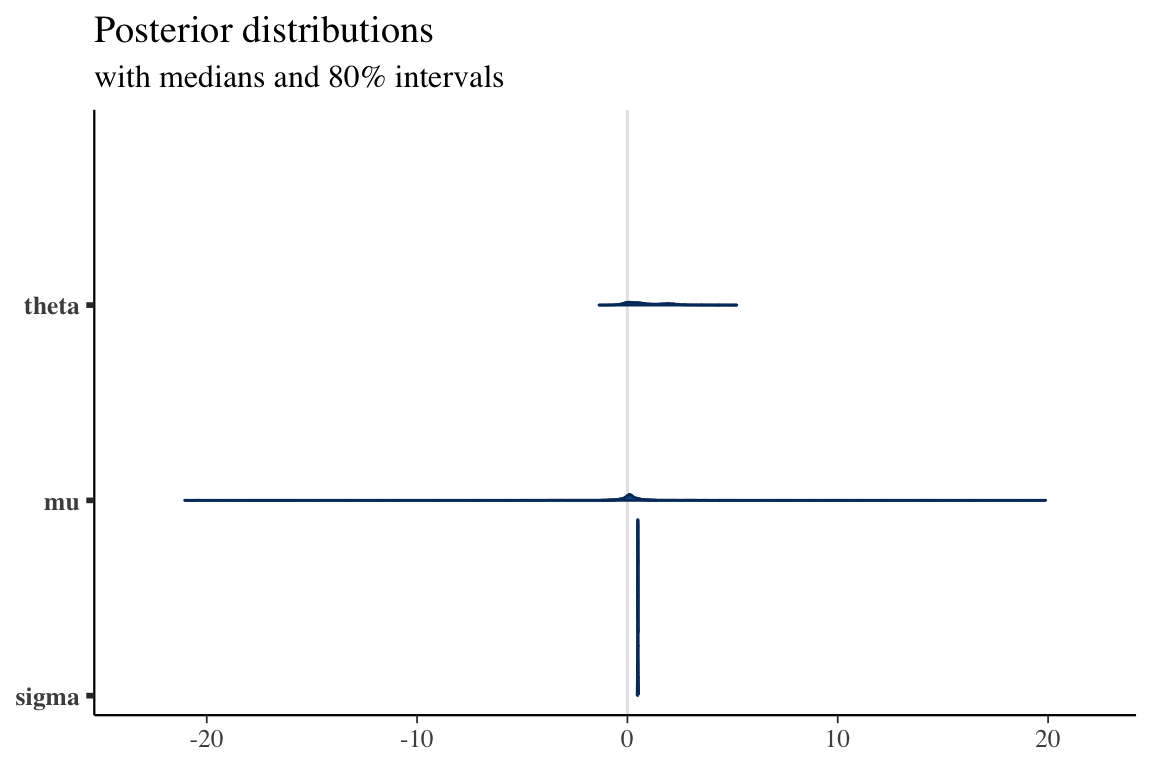
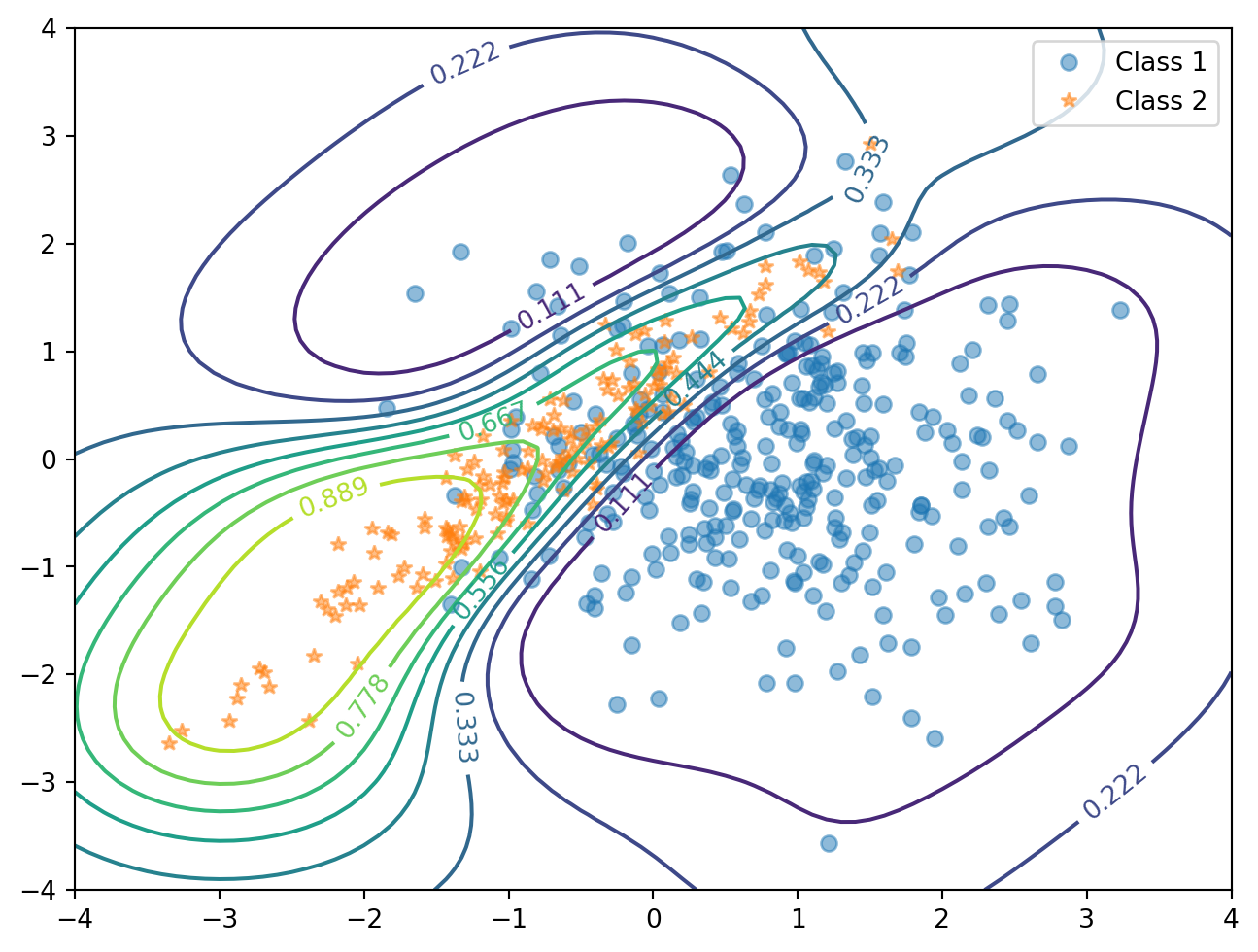
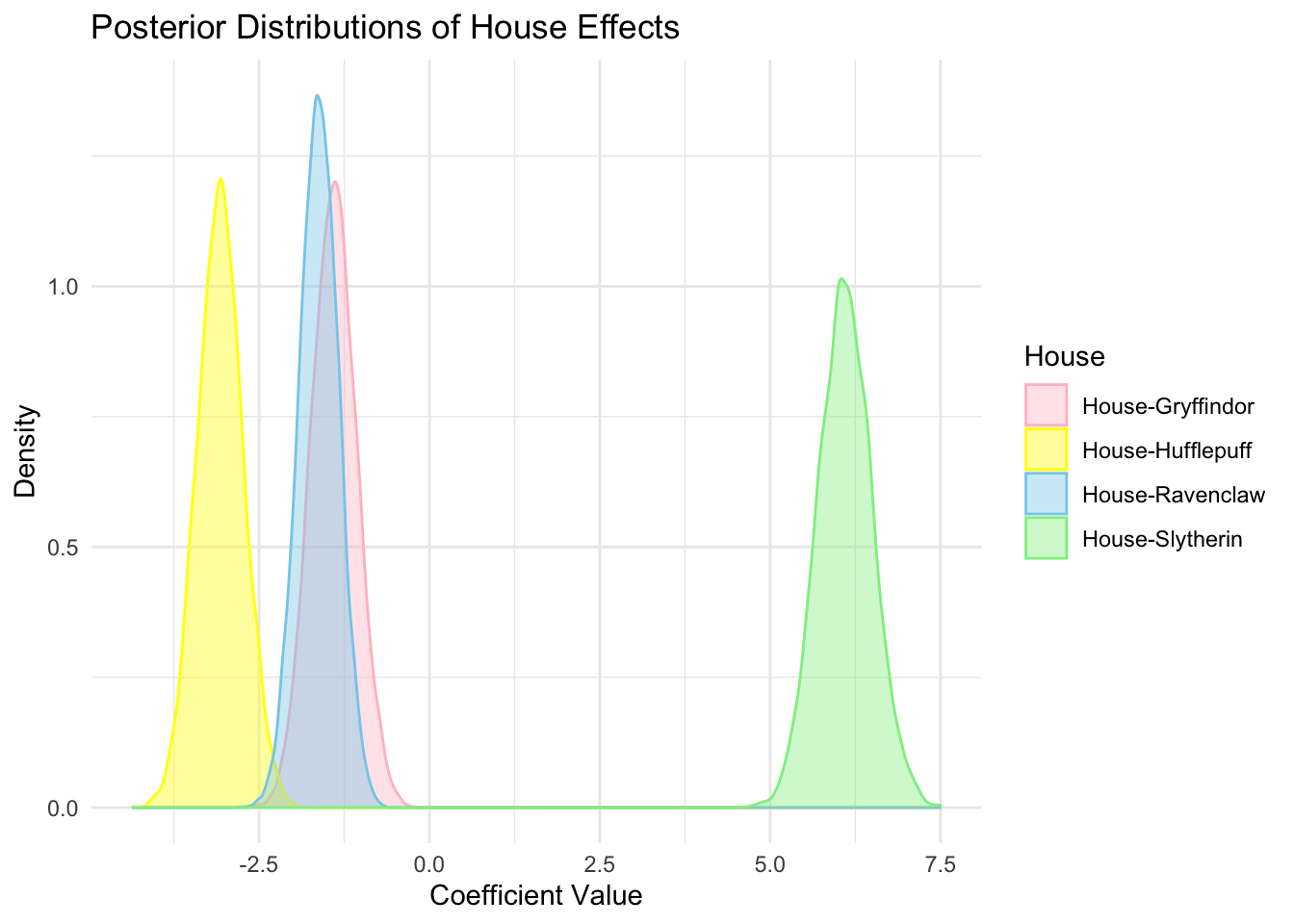
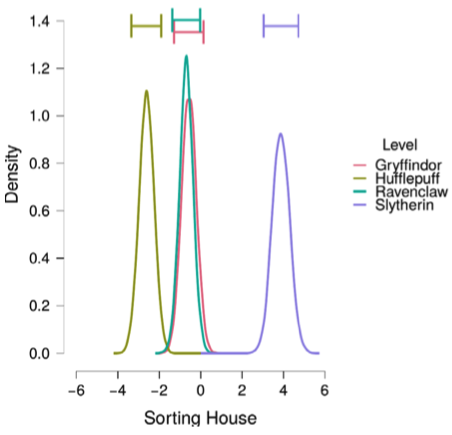
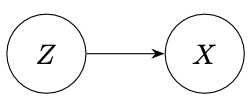
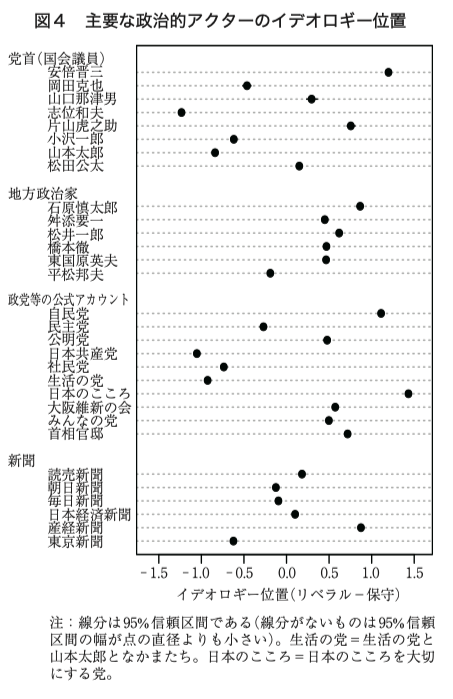
Ideal point models are 2-parameter item response model, tailored to the purpose of visualizing / measuring the ideological positions of the legislators / judges. (Bafumi et al., 2005) introduced a hierarchical structure to the model to deal with the problem of identifiability. In this article, we re-examine the model and show that the posterior distribution of the parameters (ideal points) is still bimodal, indicating its weak identifiability.
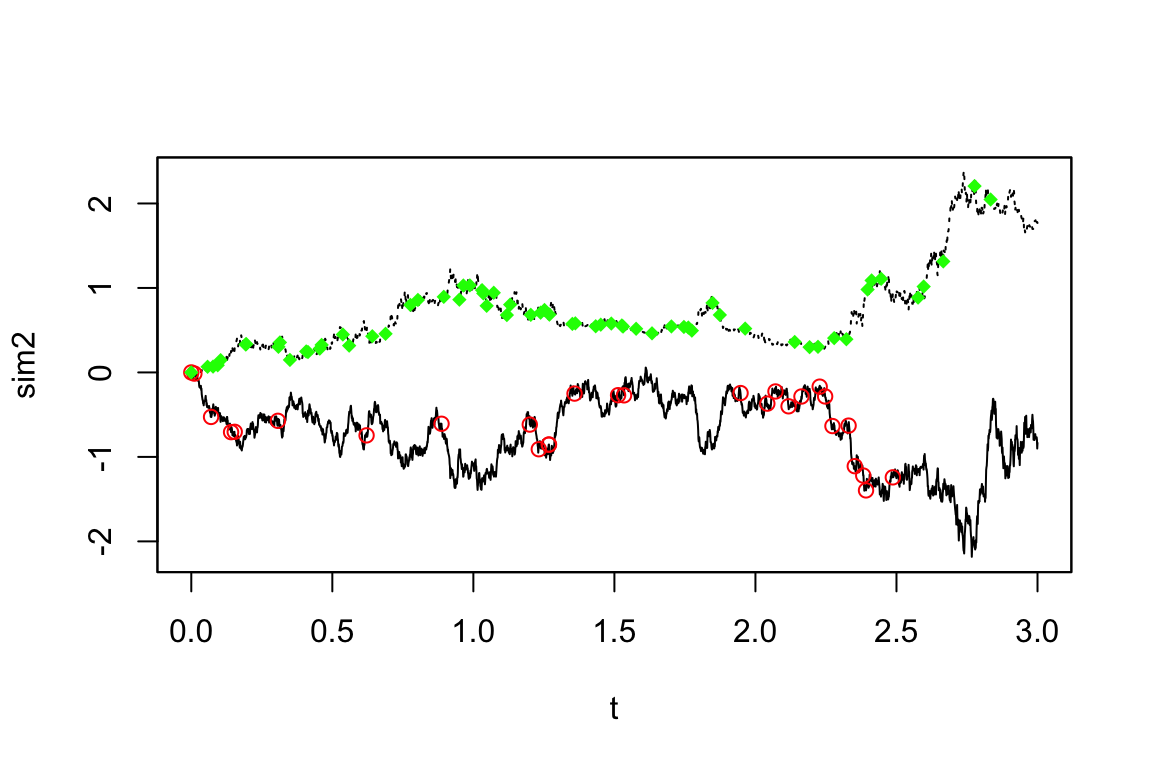
連続・離散を往来する MCMC サンプラー
Sticky PDMP によるベイズ変数選択
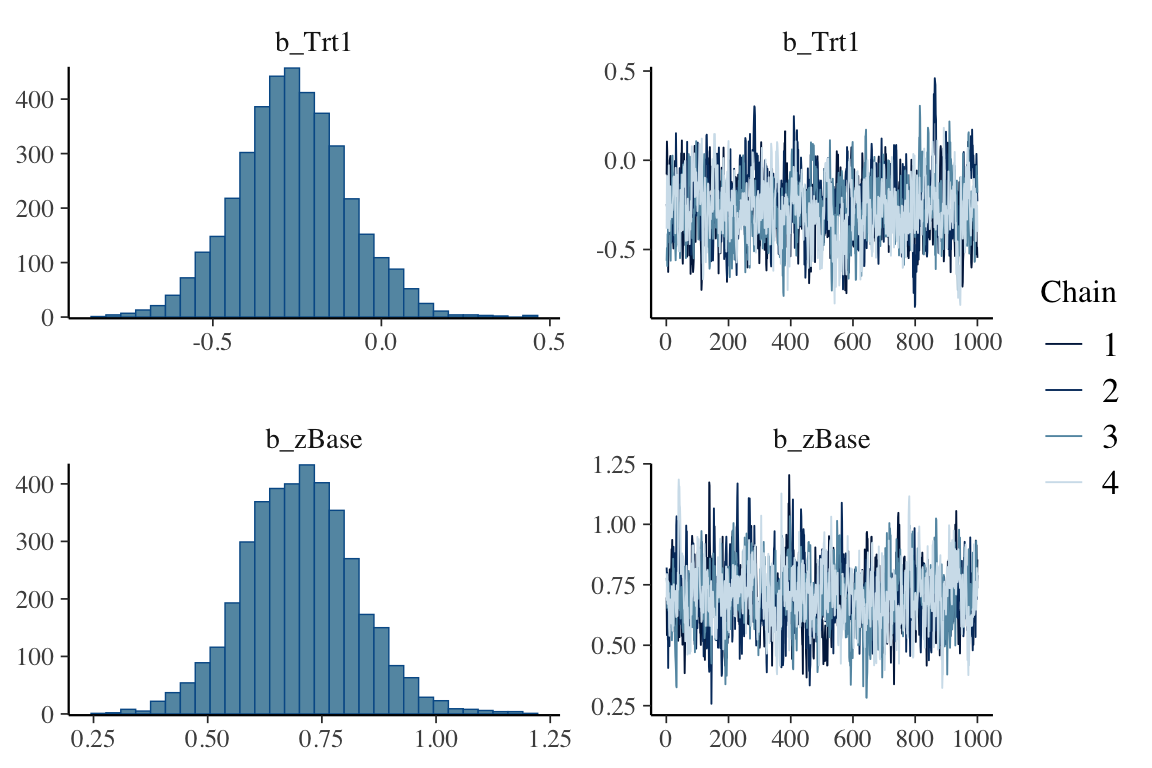
brms を用いたノンパラメトリック回帰分析
階層ベイズ理想点解析
ベイズ変数選択
ベイズ理想点解析
理想点解析とは,政治学において国会議員のイデオロギーを定量化・視覚化する方法論である.この手法は多くの側面を持ち,項目反応モデルであると同時に多次元展開法 (MDU: Multidimensional Unfolding)でもある.
PDMPFlux.jl パッケージ
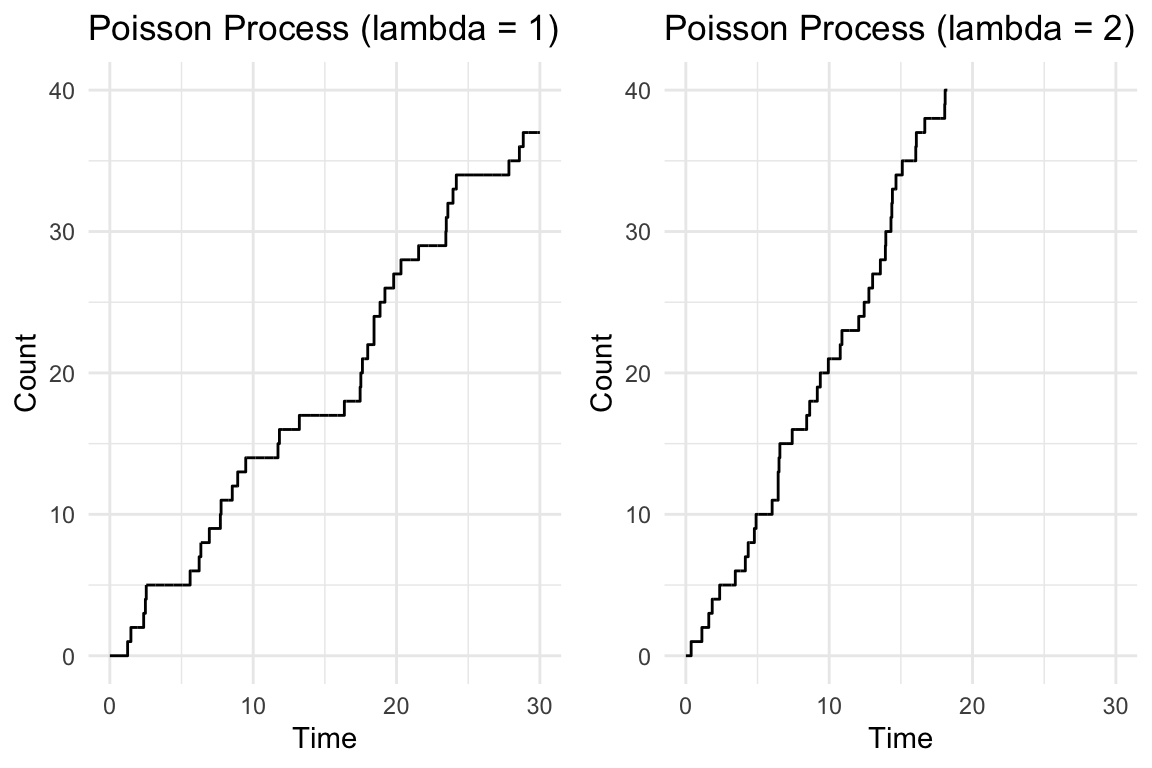
PDMP / 連続時間 MCMC とは 2018 年に以降活発に研究が進んでいる新たな MCMC アルゴリズムである. 実用化を遅らせていた要因として,種々のモデルに統一的な実装が難しく,モデルごとにコードを書き直す必要があったことが挙げられたが, この問題は自動微分の技術と,(Corbella et al., 2022), (Sutton and Fearnhead, 2023) らの適応的で効率的な Poisson 点過程のシミュレーションの研究によって解決されつつある. ここでは (Andral and Kamatani, 2024) の Python パッケージ pdmp_jax とこれに基づく Julia パッケージ PDMPFlux.jl を紹介する.
Lévy 過程に駆動される SDE のエルゴード性
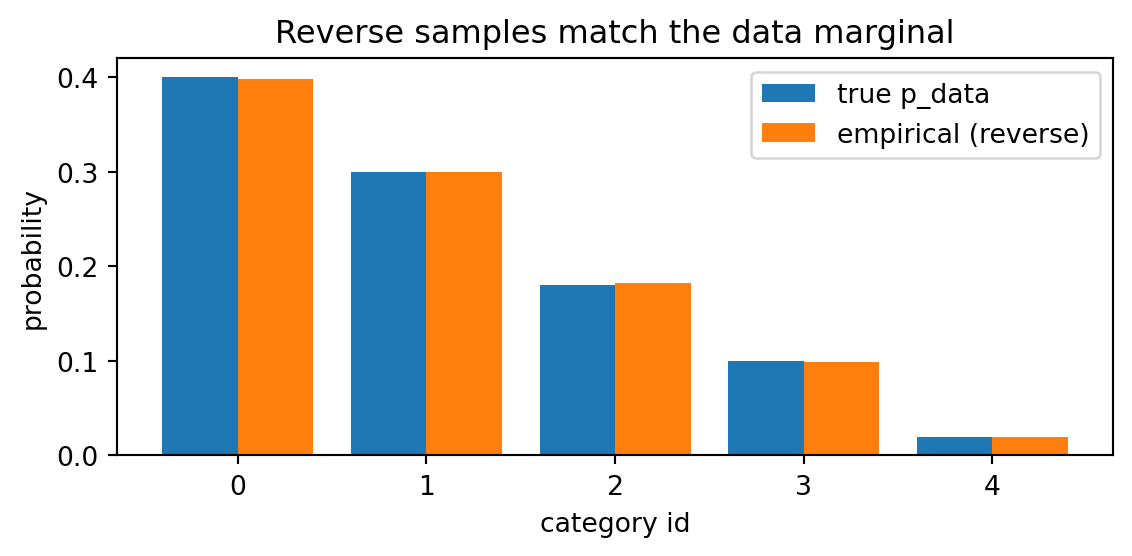
雑音除去拡散サンプラー
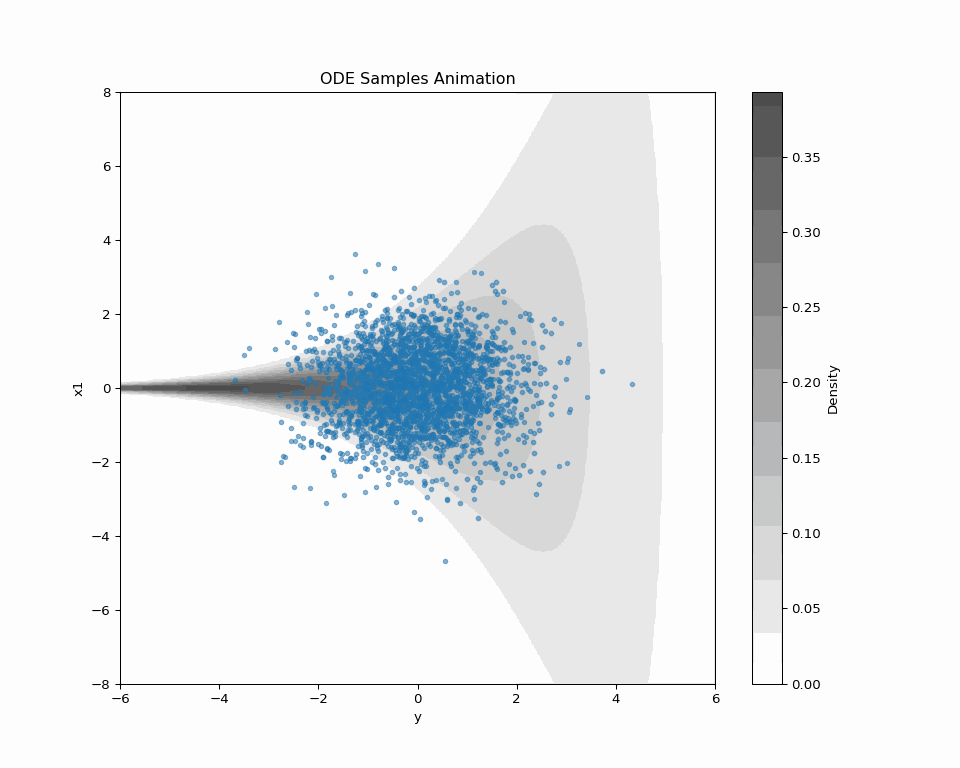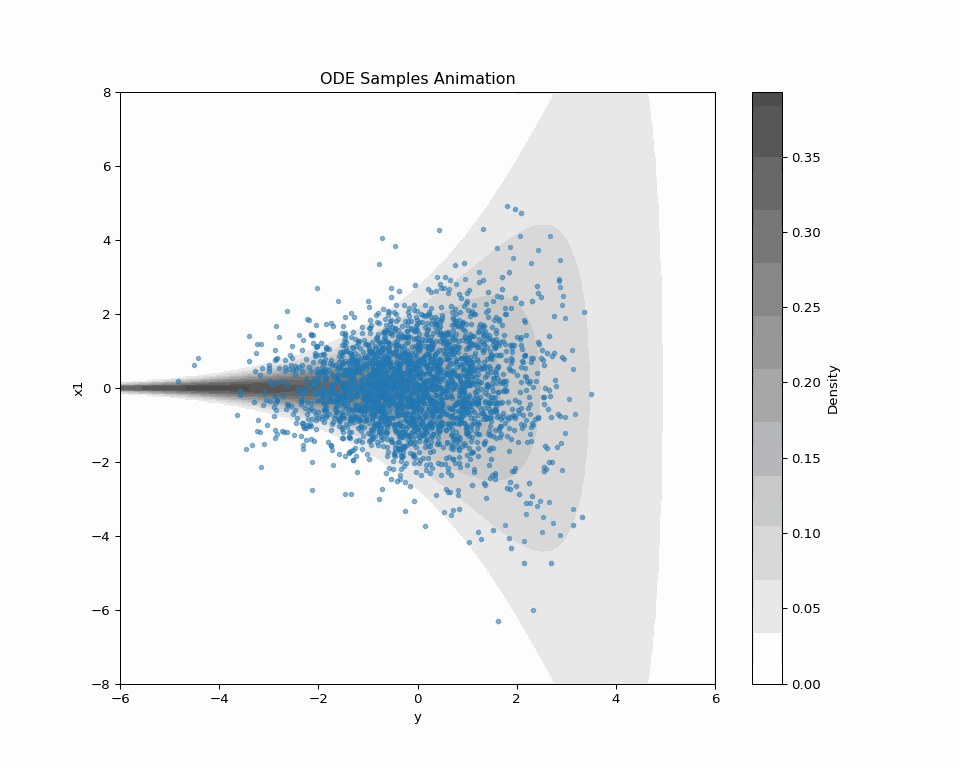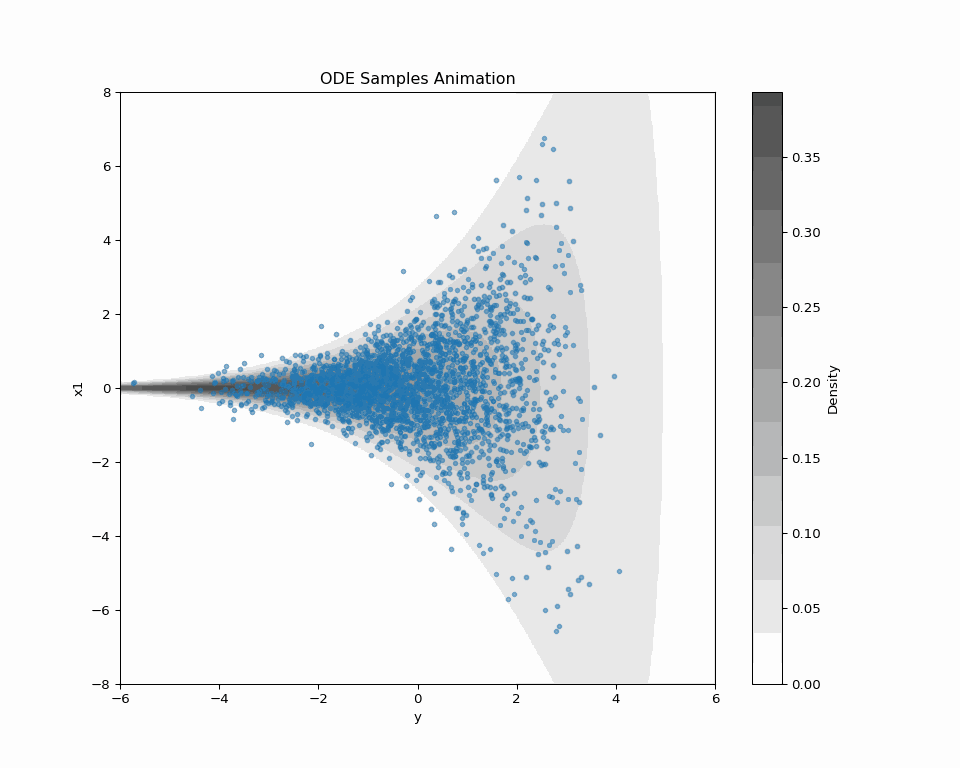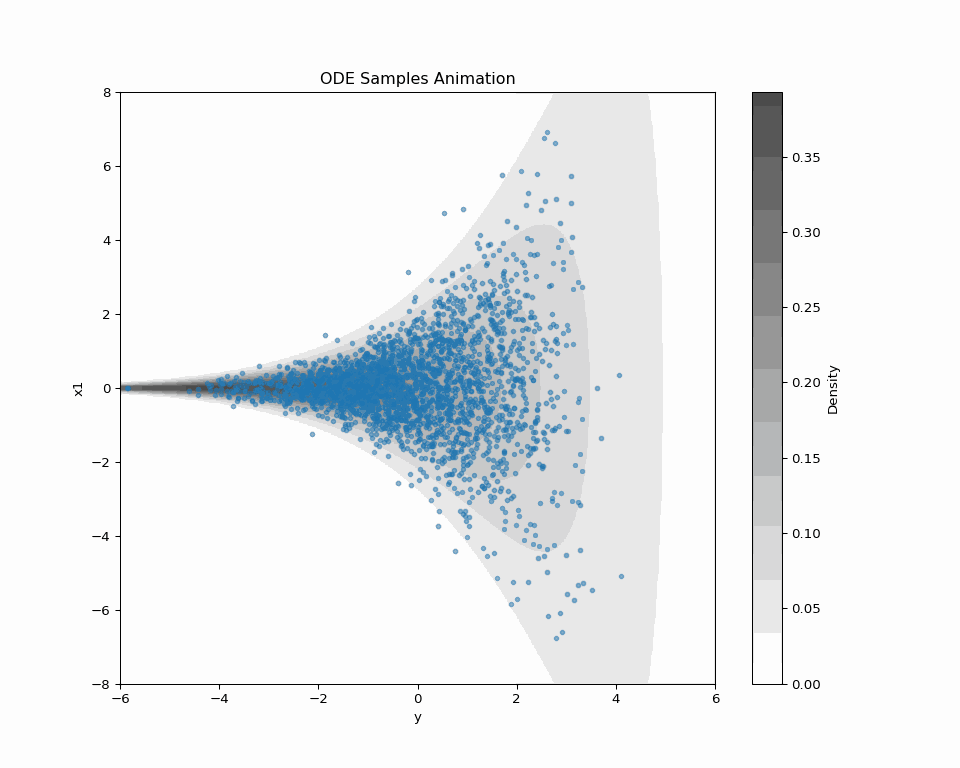
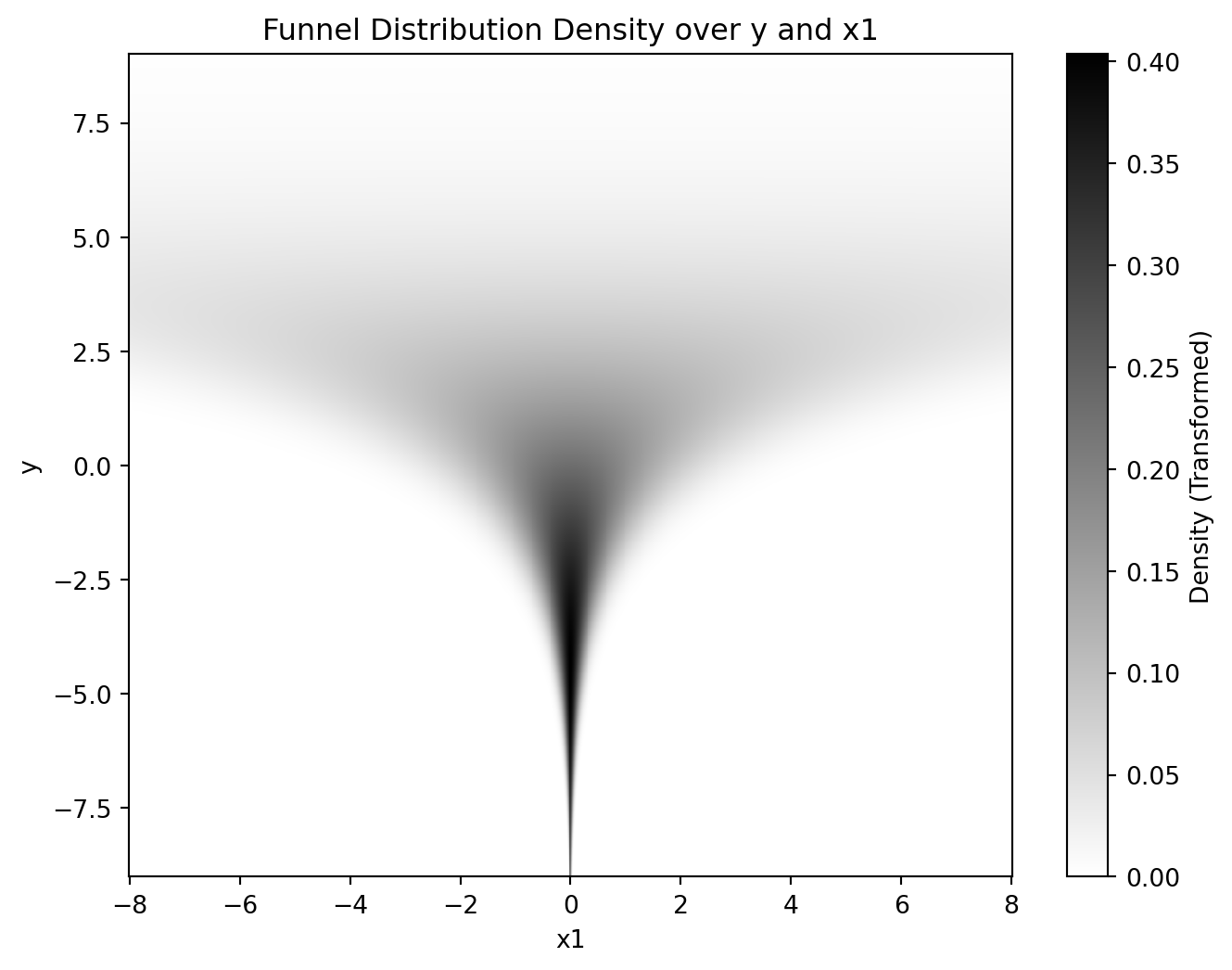
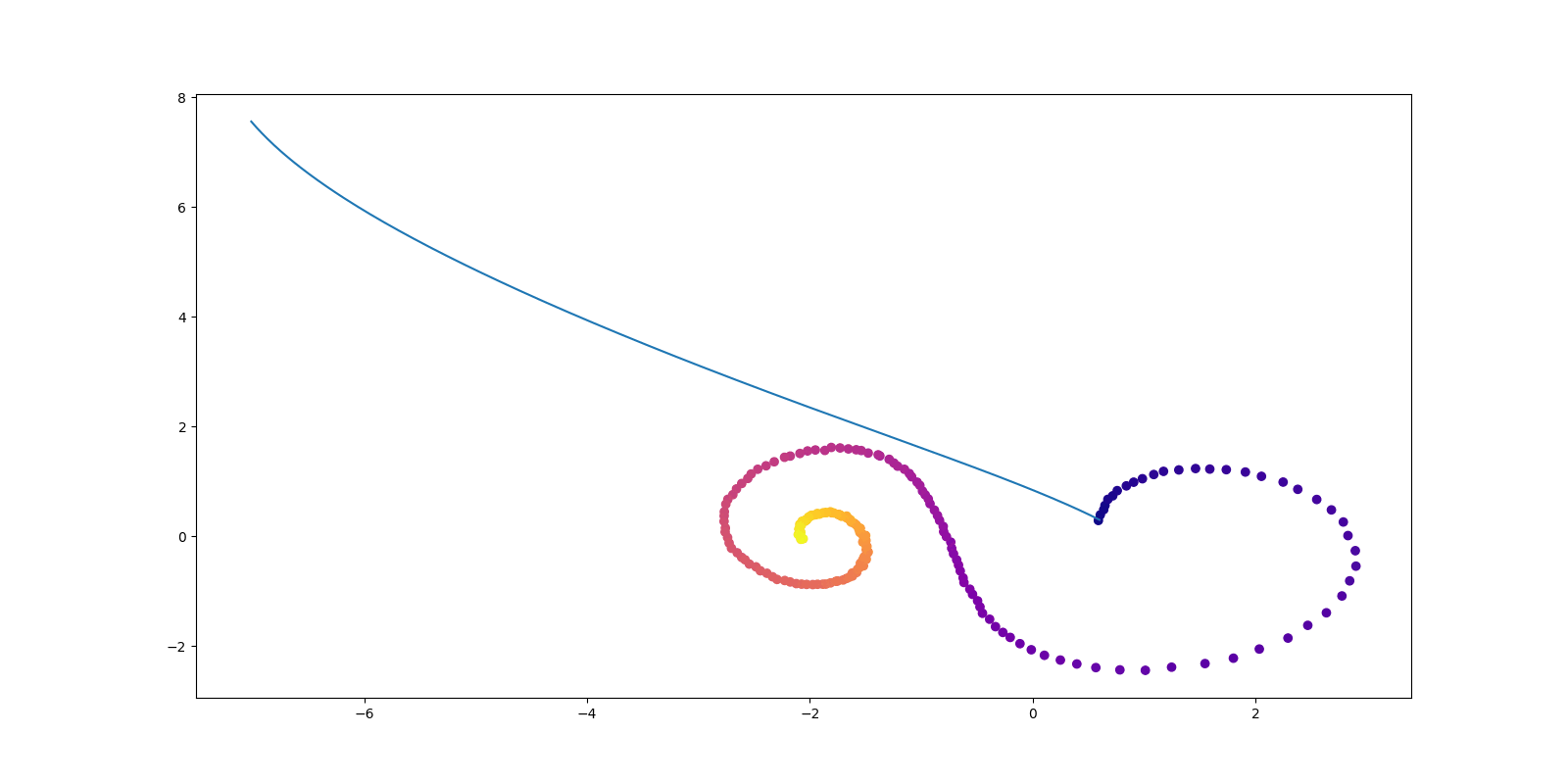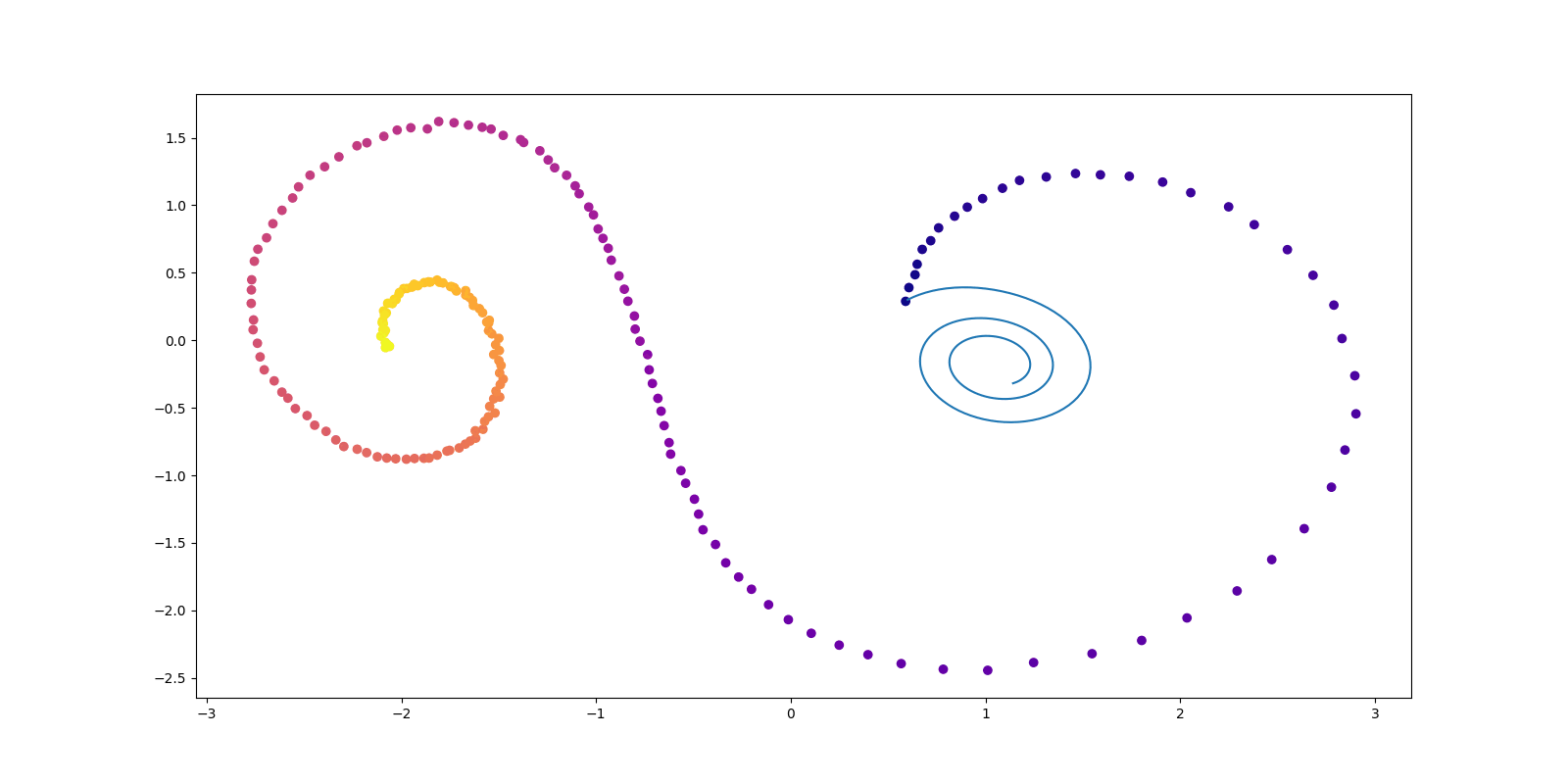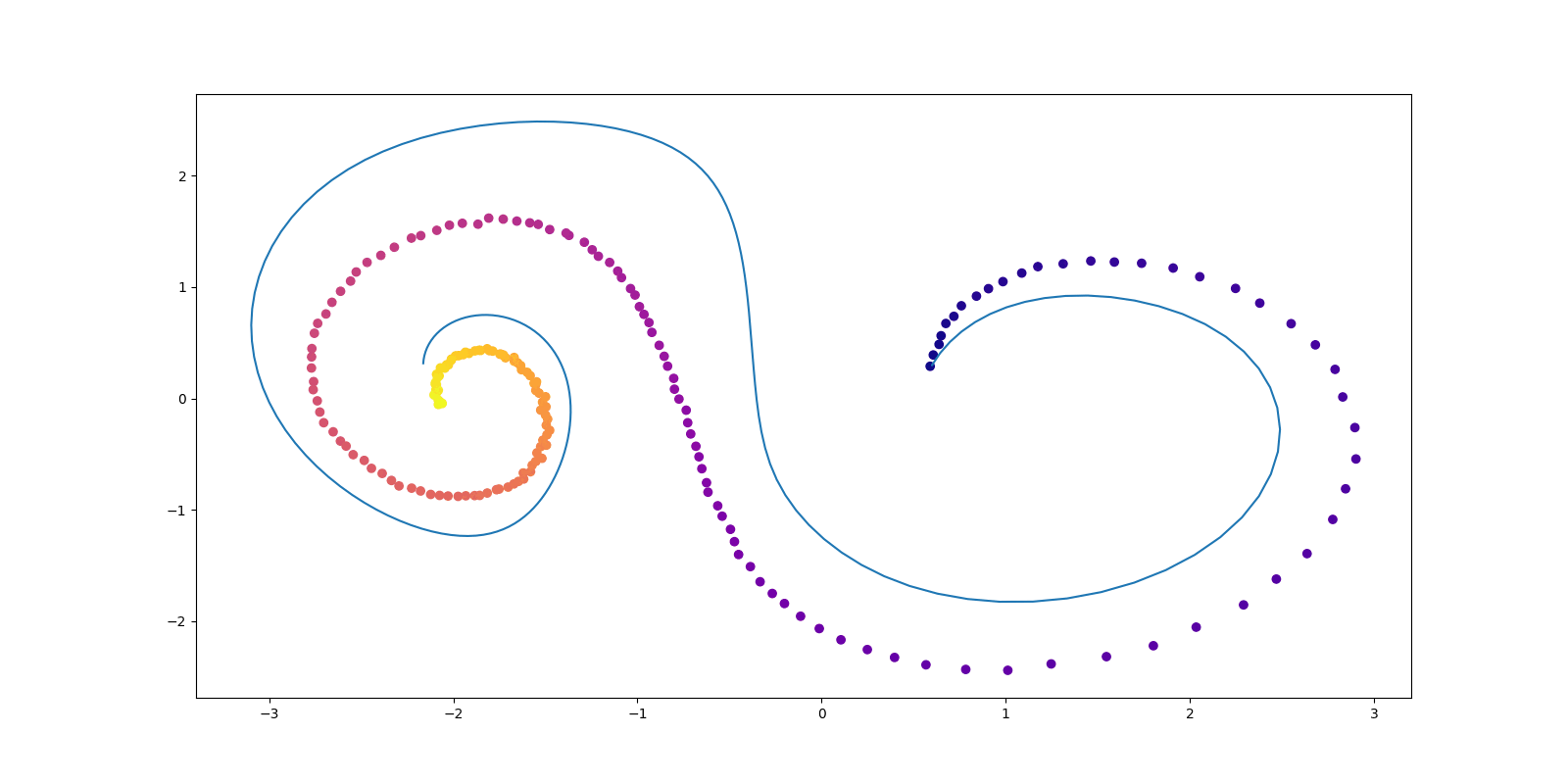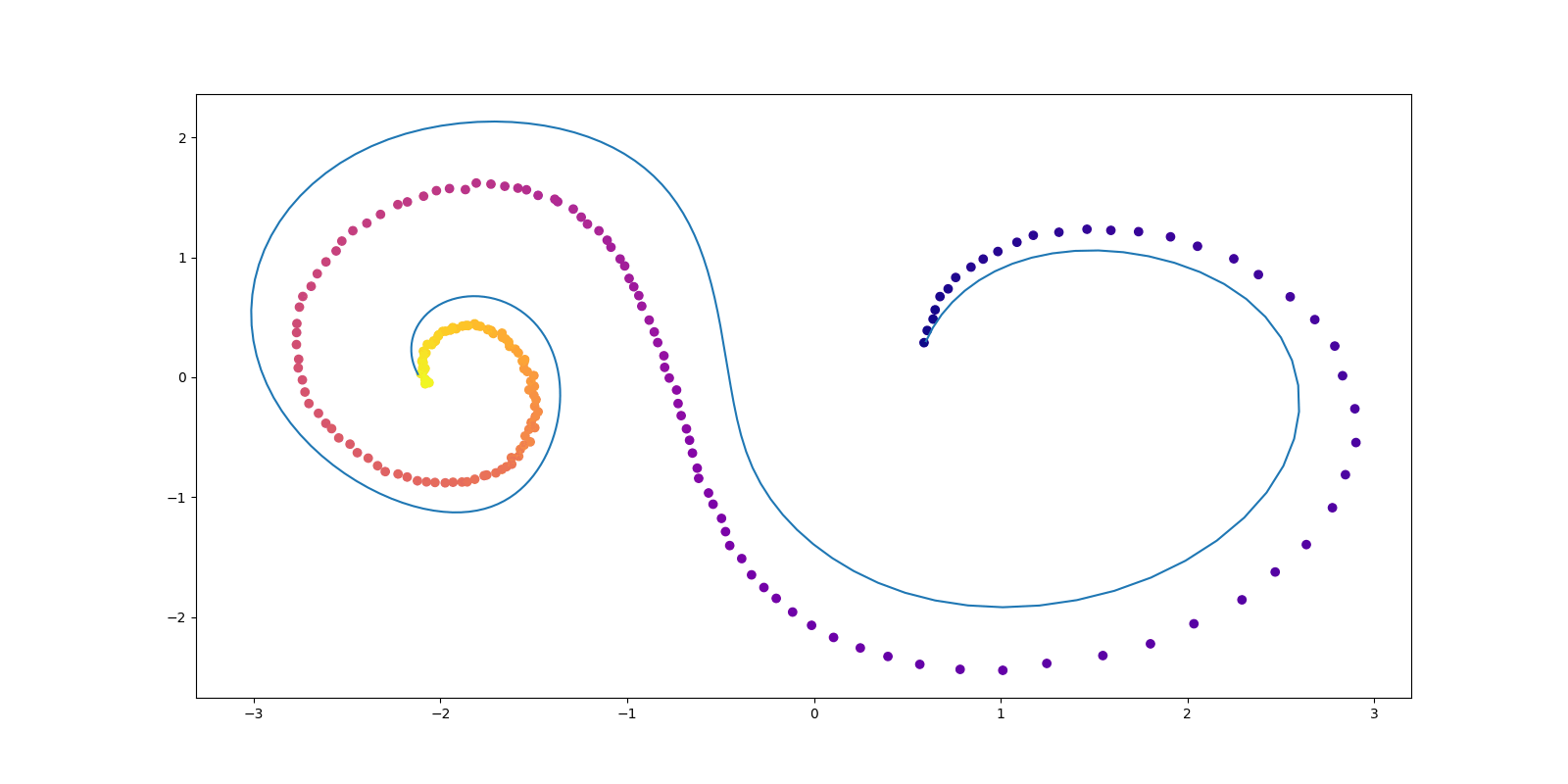
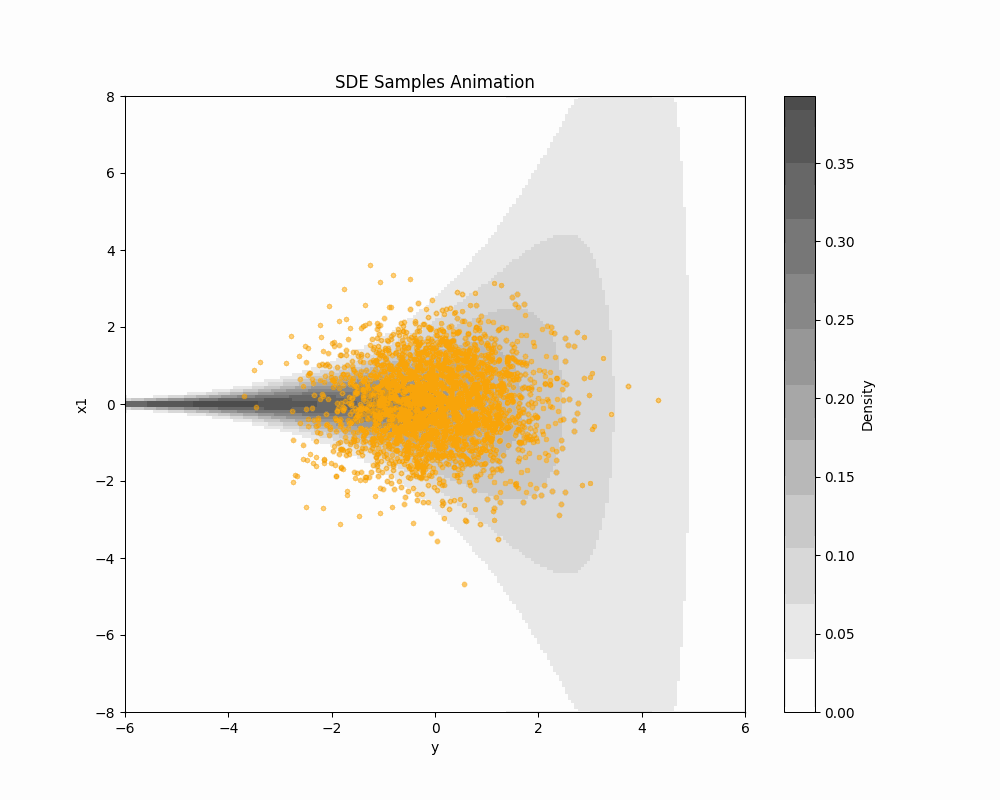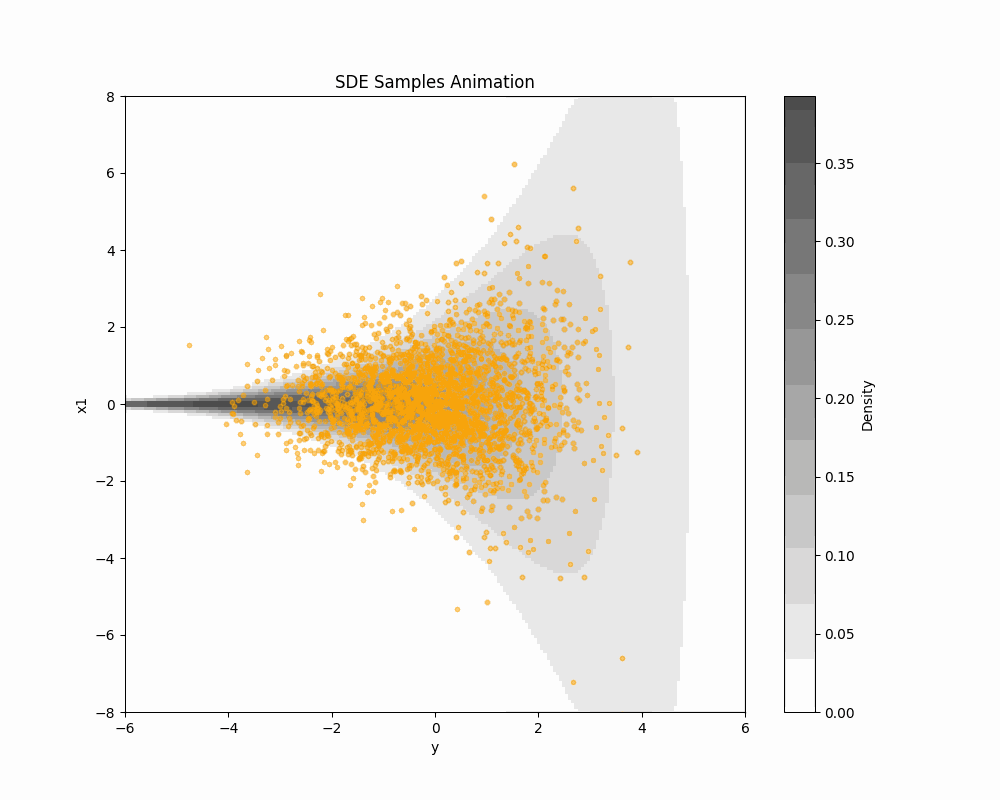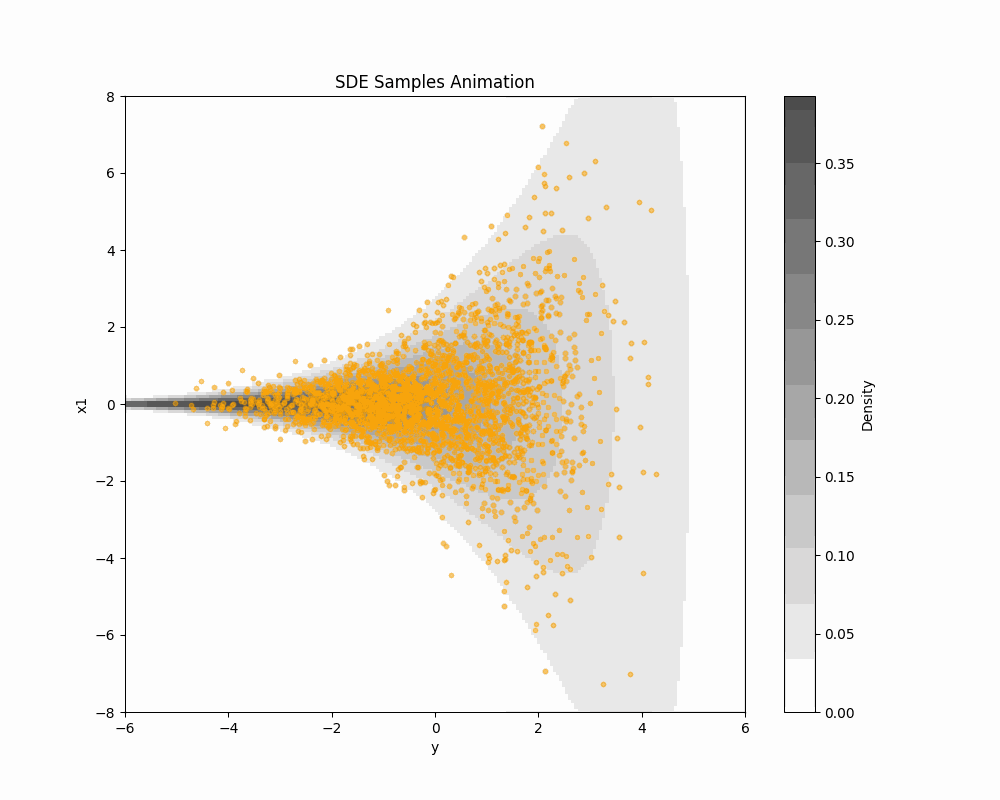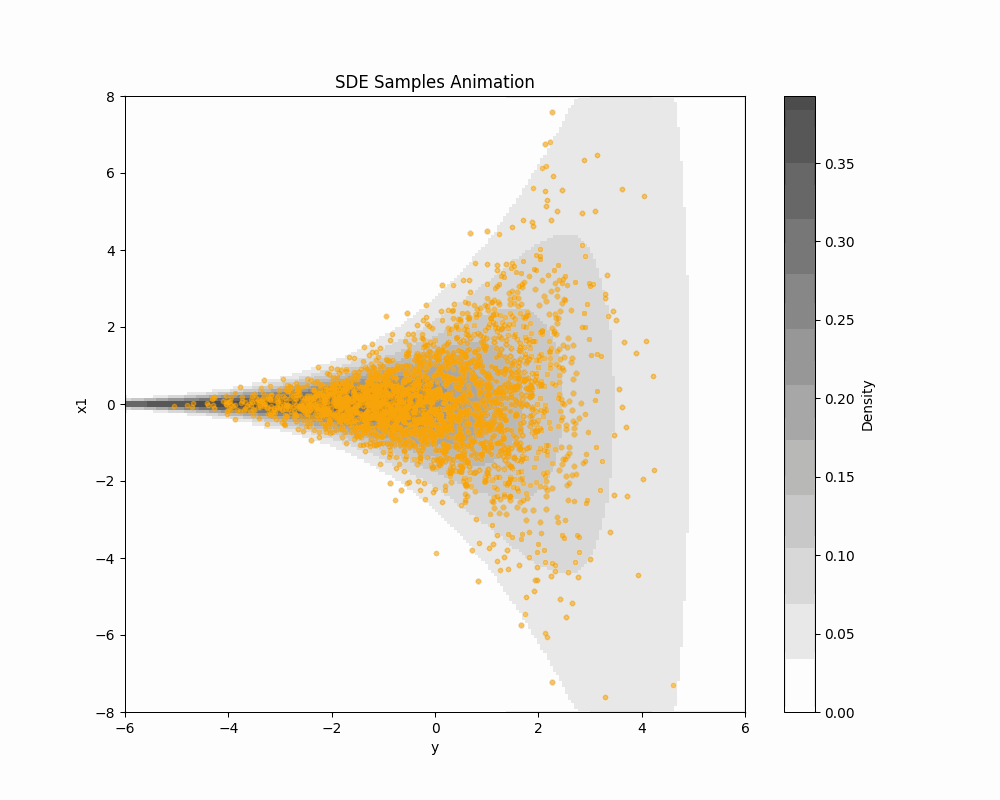
(Vargas et al., 2023) の DDS (Denoising Diffusion Sampler) は変分推論のように逆 KL 乖離度を最小化することを通じて,一般の確率分布からのサンプリングを可能にする方法である.今回は 公式の実装 を吟味する.
流体モデル概観
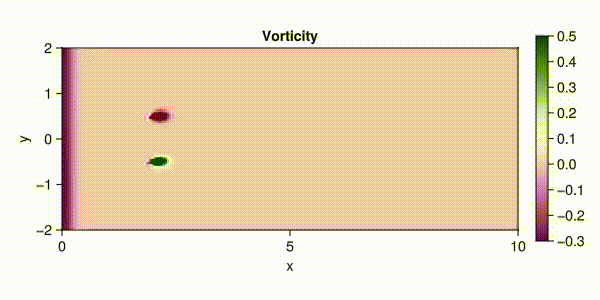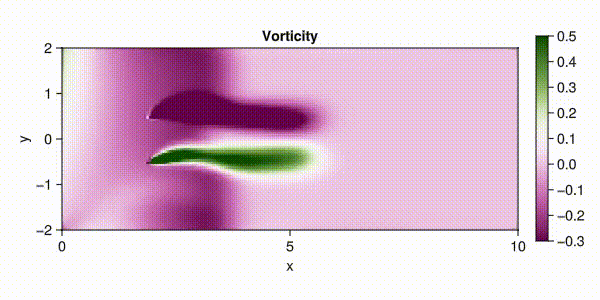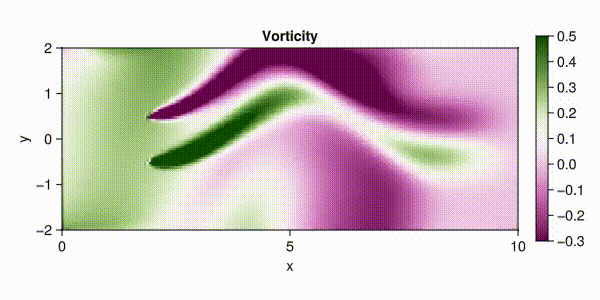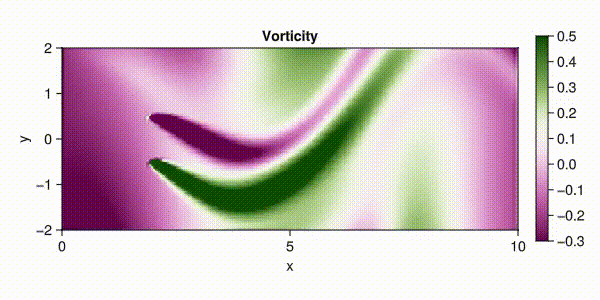
Lorenz’ 63, Lorenz’ 96 とはそれぞれ (Lorenz, 1963), (Lorenz, 1995) によって導入された大気モデルである. 前者はバタフライ効果の語源ともなった,最初に特定されたカオス力学系でもある. Navier-Stokes 方程式は流体の運動を記述する方程式である. これらはいずれもデータ同化・軌道推定技術のベンチマークとして用いられている. ここでそれぞれのモデルの数学的性質と Julia を通じたシミュレーションの方法をまとめる.
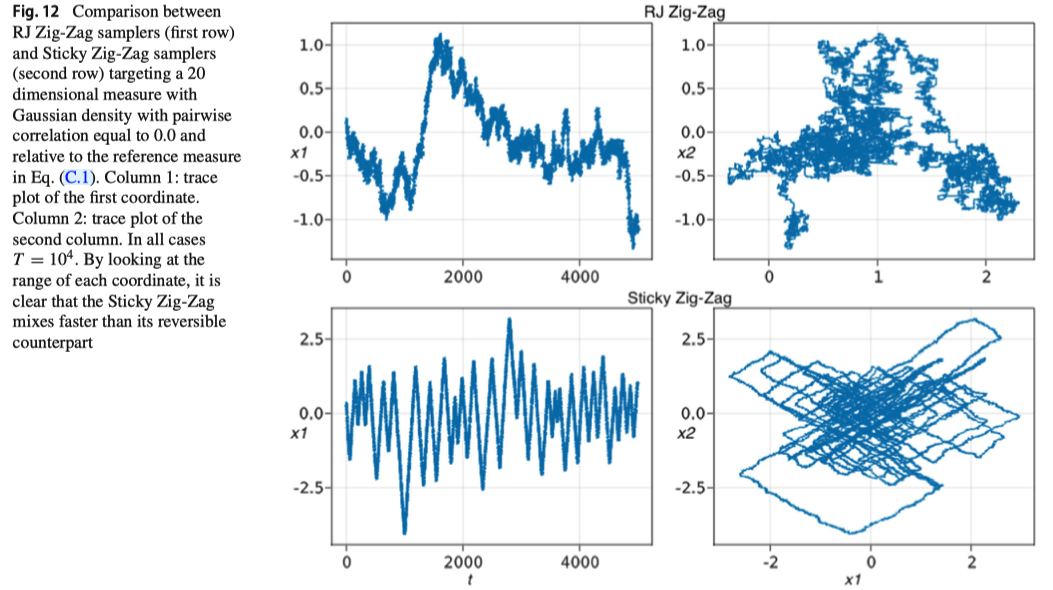
超次元 Zig-Zag サンプラー
超次元 Zig-Zag サンプラー
ベイズ分散分析のモデル解析
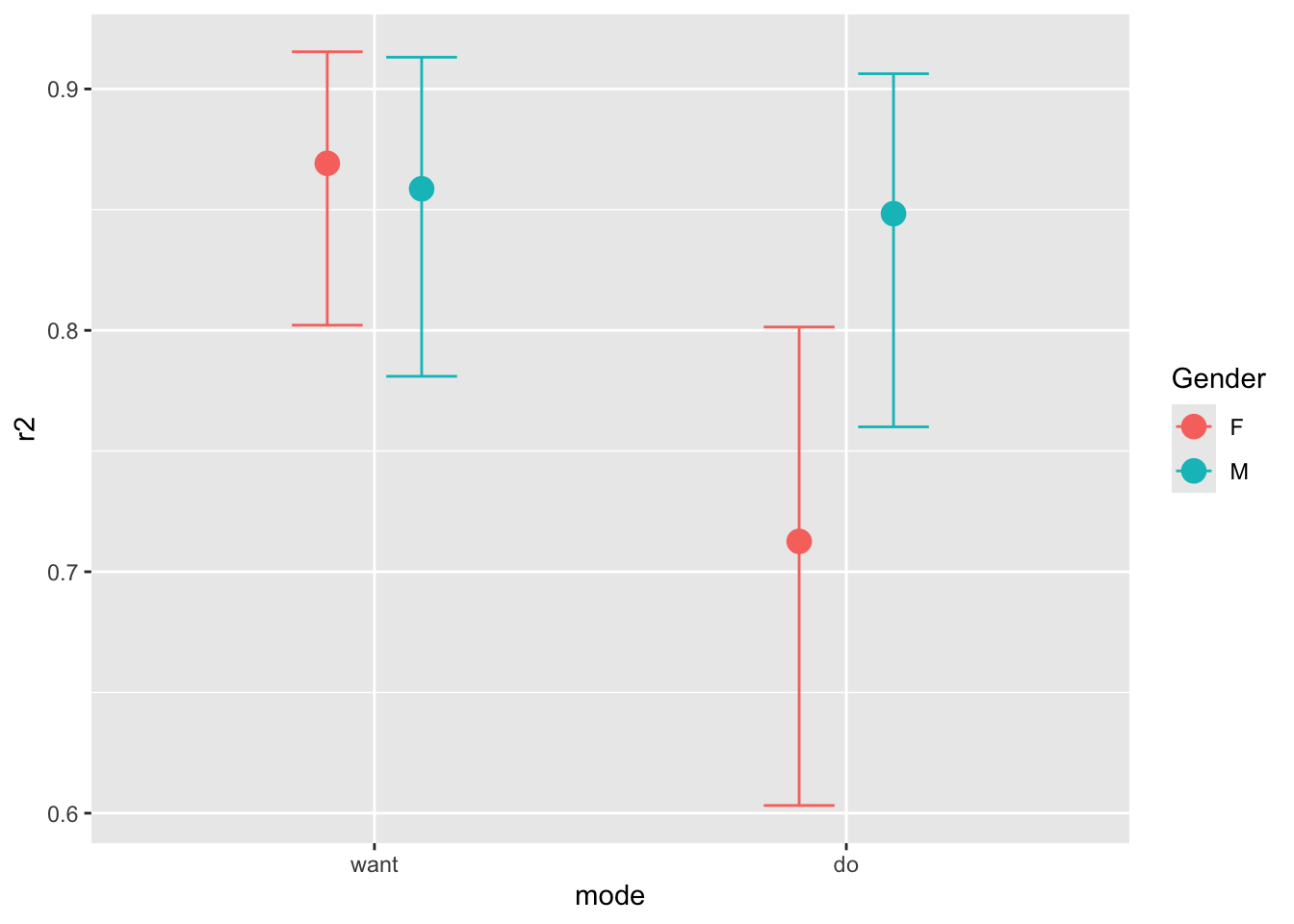
心理学などの人間を対象にする研究では変数の数が多く,正しいモデルを見つけるために分散分析 (ANOVA) が広く用いられてきた. しかし,古典的な ANOVA 手法である F-検定や t-検定は,データの一側面に着目した手法である.
ベイズ的な解析手法は,これを補完する多くの探索的な手法を提供してくれる. 特に,データに潜む極めて微妙な消息も捉えることが可能になることをここでは強調したい. このような微妙な消息を最初から想定することは難しく,ベイズの探索的な性格が真に可能にするデータ解析事例があると言えるかもしれない.
そこで本稿では (van den Bergh et al., 2020) に基づいて,「社会的なロボット」に関する心理学実験のデータに対するベイズ ANOVA (Gelman, 2005), (Rouder et al., 2012) 解析のモデルケースを紹介する. 少しずつデータの構造が見えてくる過程が,読者にうまく提示できることを願う.
ベイズデータ解析2
超次元 MCMC
Skilling-Hutchinson の跡推定量
階層モデル再論
拡散モデルからシュレディンガー橋へ
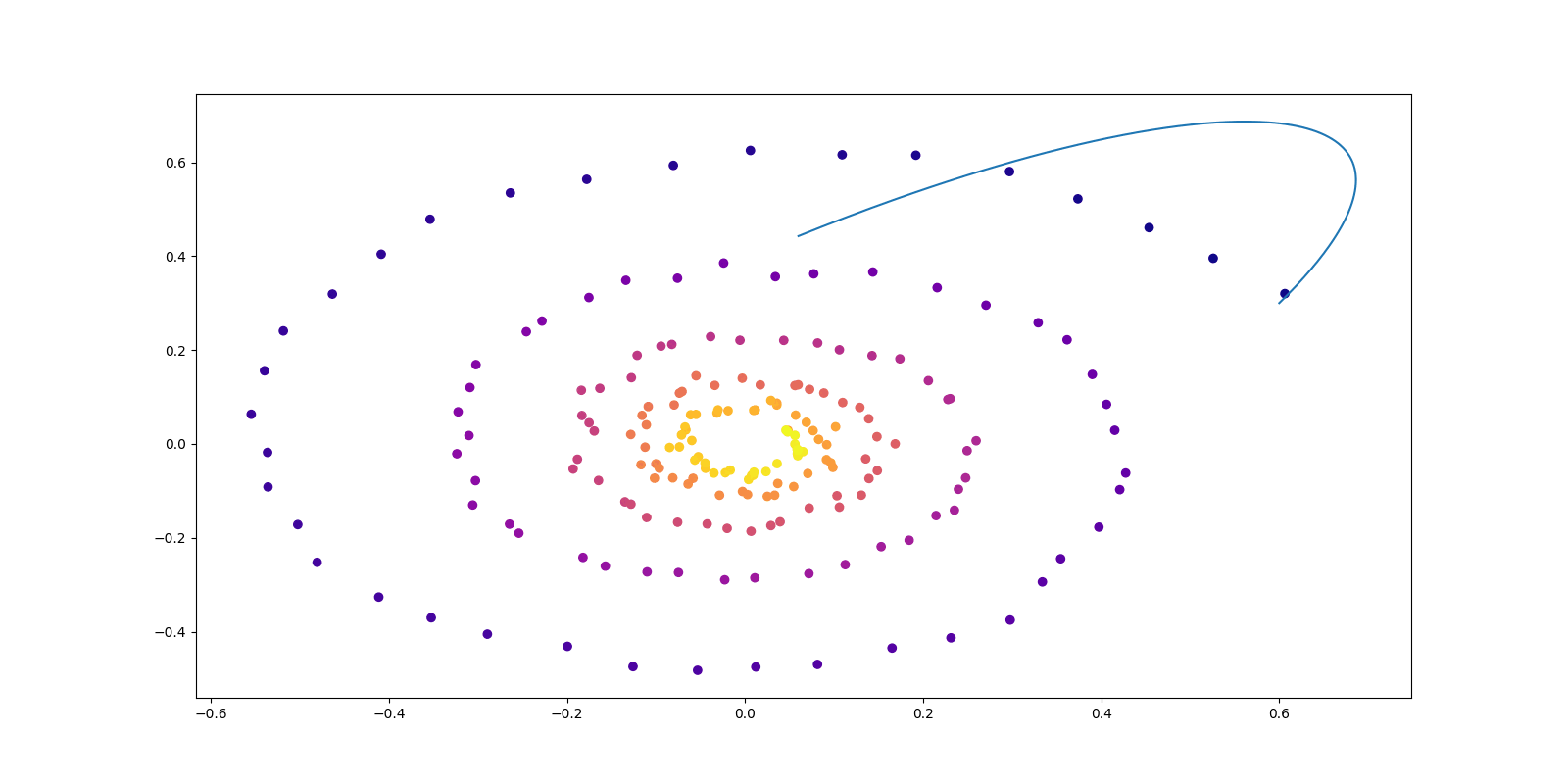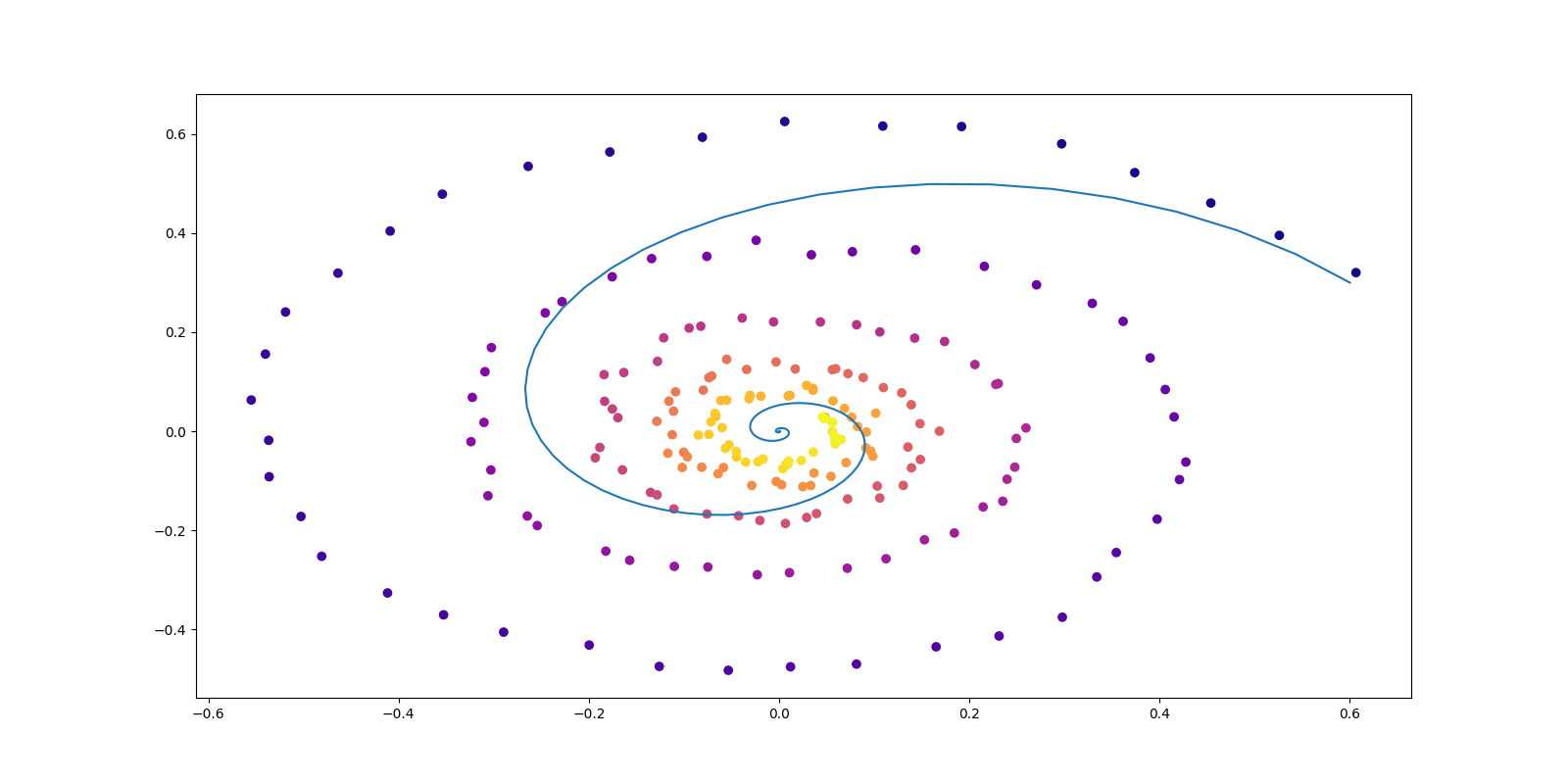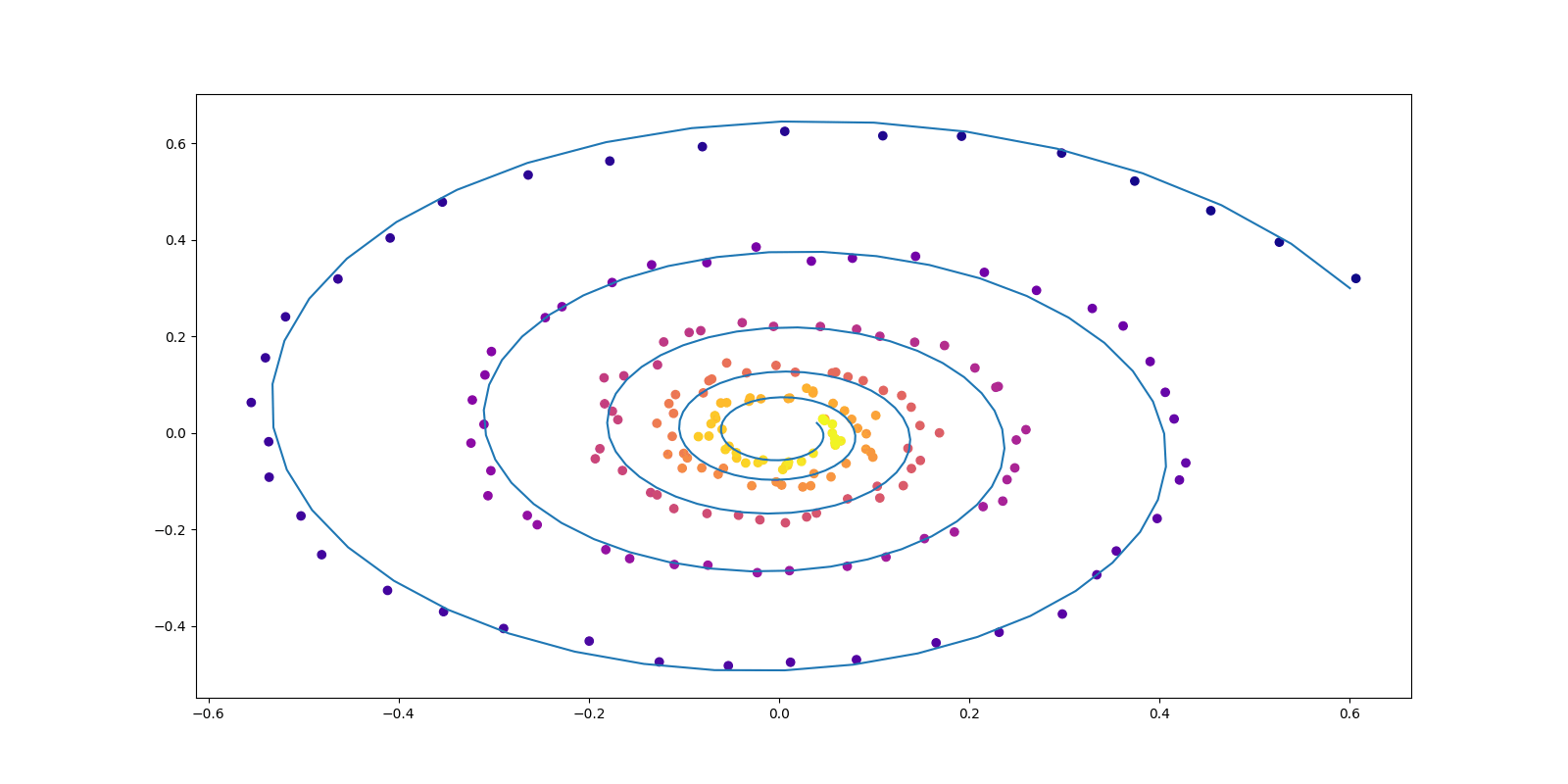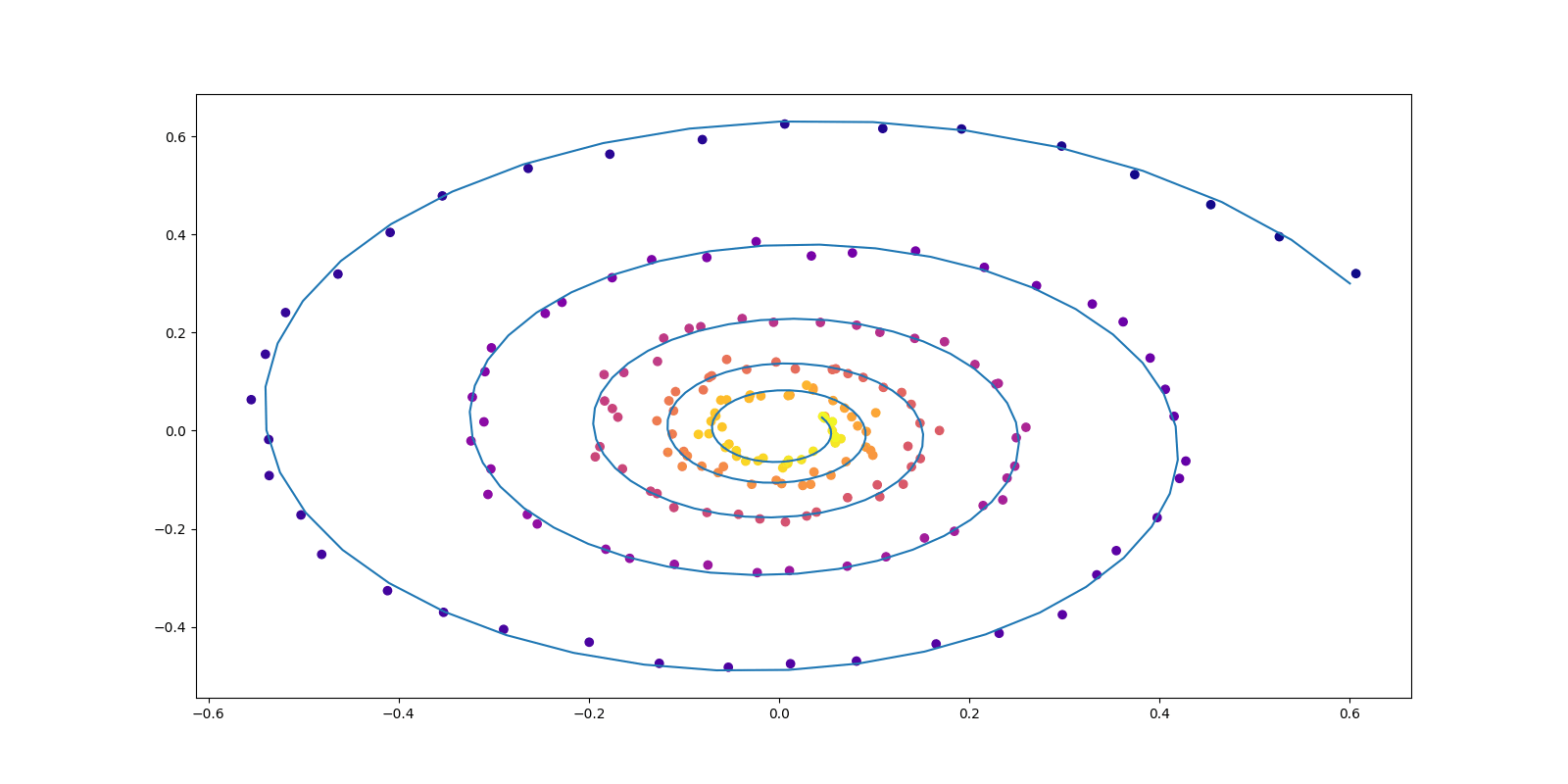
拡散モデルは「データ過程をノイズに還元する Langevin ダイナミクスを時間反転する」という発想に基づいており,画像と動画の生成・条件付き生成タスクに関して 2024 年時点で最良の方法の1つである. この発想を正確なサンプリング法に昇華するためには,(Deming and Stephan, 1940) の Iterative Proportional Fitting アルゴリズムを用いることができる. この方法は拡散モデルによる条件付き生成の加速法として (Shi et al., 2022) によって提案された. こうして得る拡散過程は Schrödinger Bridge とも呼ばれ,エントロピー最適輸送と深い関わりを持つ.
雑音除去拡散サンプラー
(Vargas et al., 2023) の DDS (Denoising Diffusion Sampler) は変分推論のように逆 KL 乖離度を最小化することを通じて,一般の確率分布からのサンプリングを可能にする方法である.
Schrödinger 橋によるサンプリング
(Vargas et al., 2023) の DDS (Denoising Diffusion Sampler) は変分推論のように逆 KL 乖離度を最小化することを通じて,一般の確率分布からのサンプリングを可能にする方法である. 本記事では Schrödinger 橋を用いて DDS を正確にすることを考える.
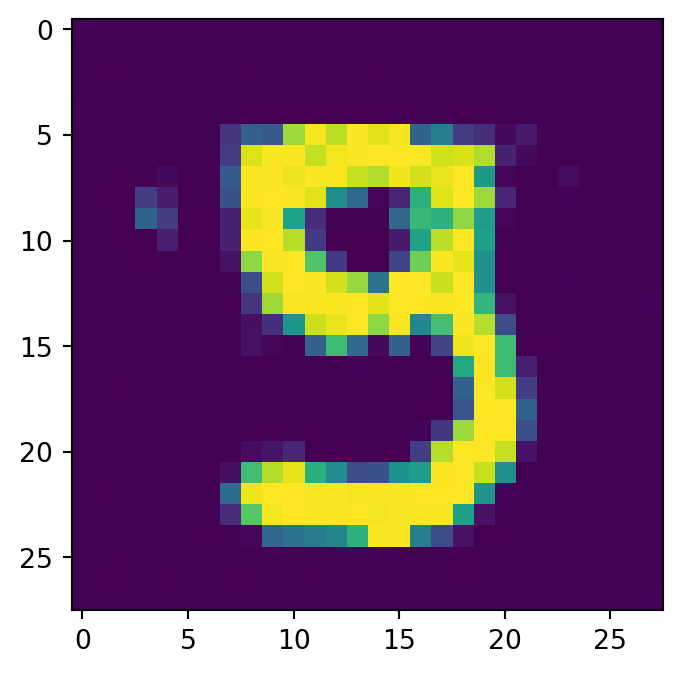
拡散モデルによる事後分布サンプリング
理想点解析・多次元展開法・項目応答理論
理想点解析とは,政治学においてイデオロギーを定量化する方法論である.この手法は多くの側面を持ち,多次元展開法 (MDU: Multidimensional Unfolding) であると同時に項目反応モデルでもある.初めに政治学における理想点解析の目的と役割を概観し,続いて多次元展開法と項目反応理論の2つの観点から理想点解析を眺める.
Metropolis-Hastings サンプラー
Julia による MCMC サンプリング
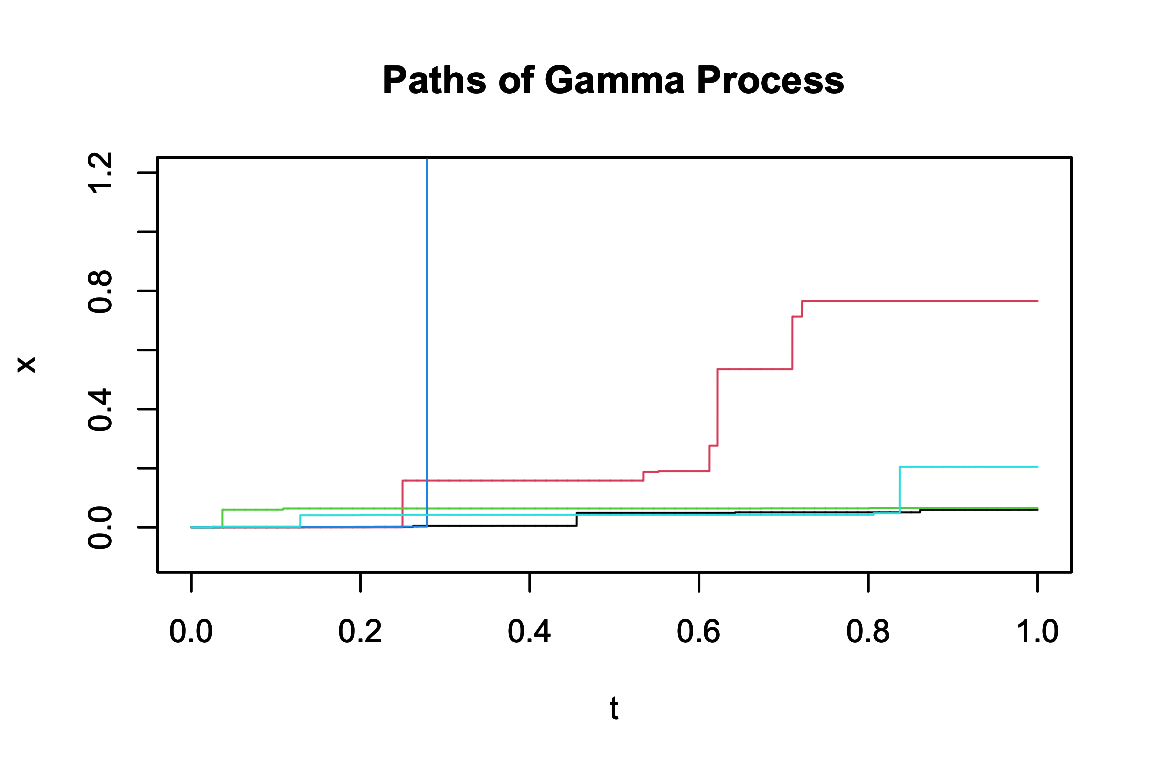
Lévy 過程を見てみよう
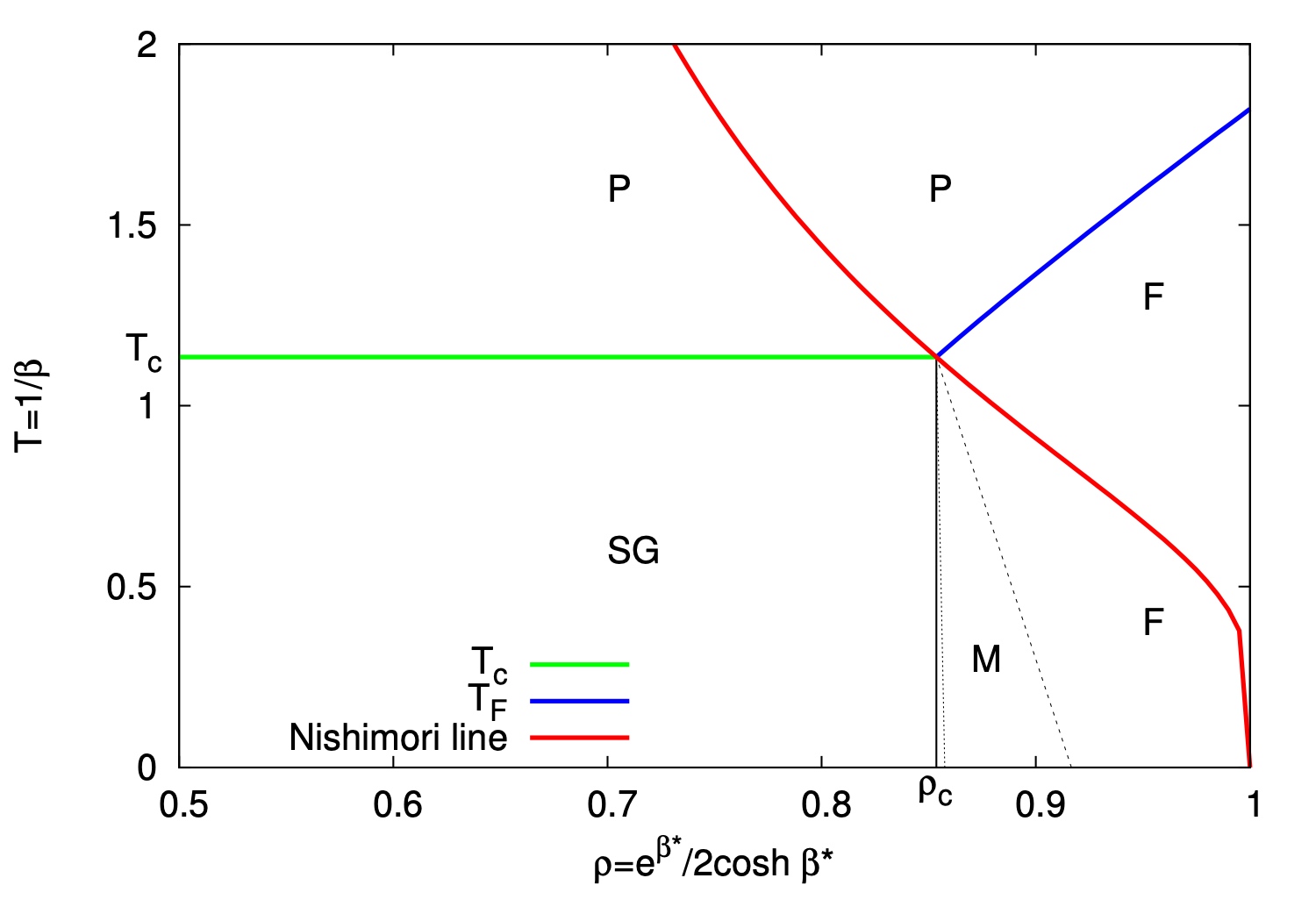
ベイズ統計学とスピングラス
Ornstein-Uhlenbeck 過程を見てみよう
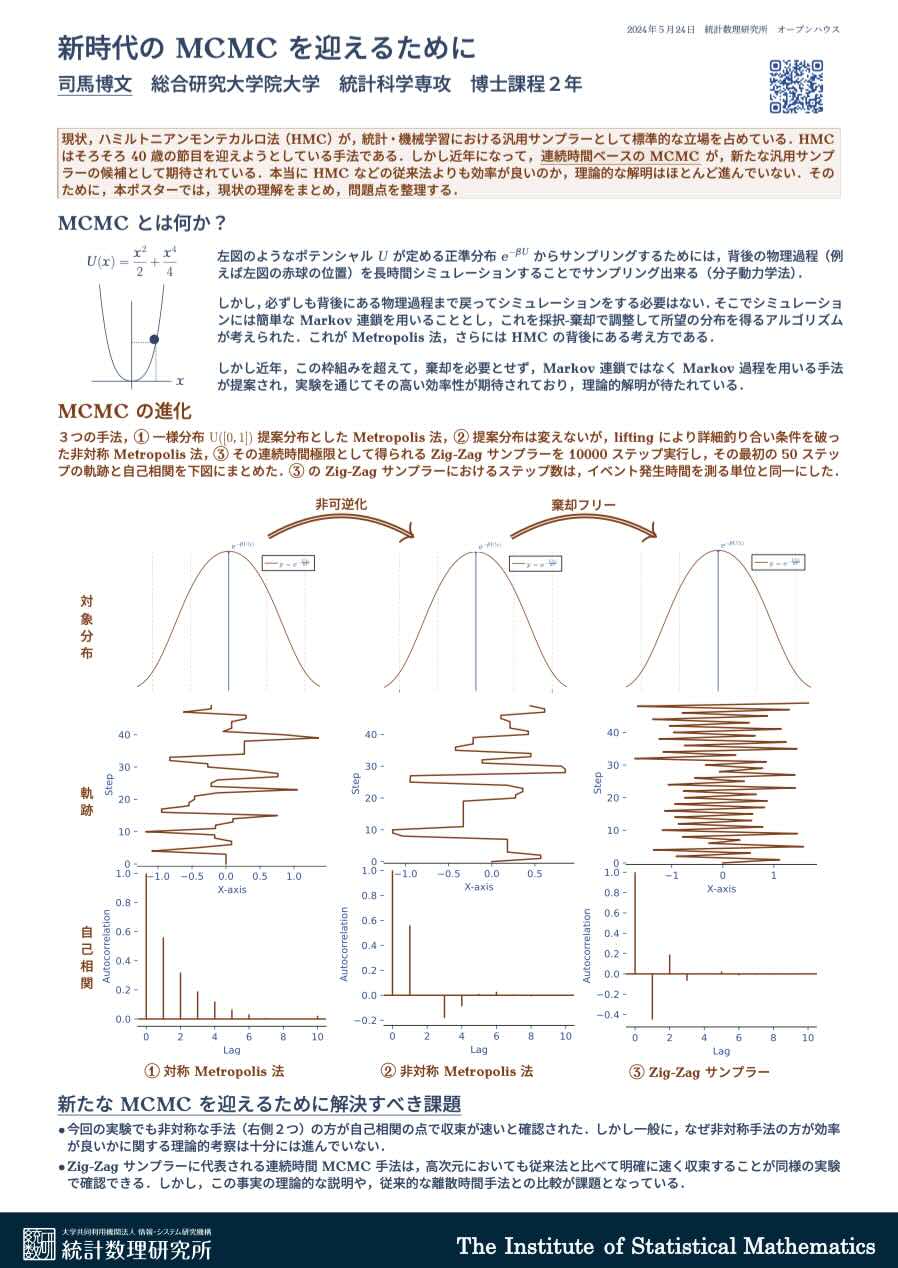
新時代の MCMC を迎えるために
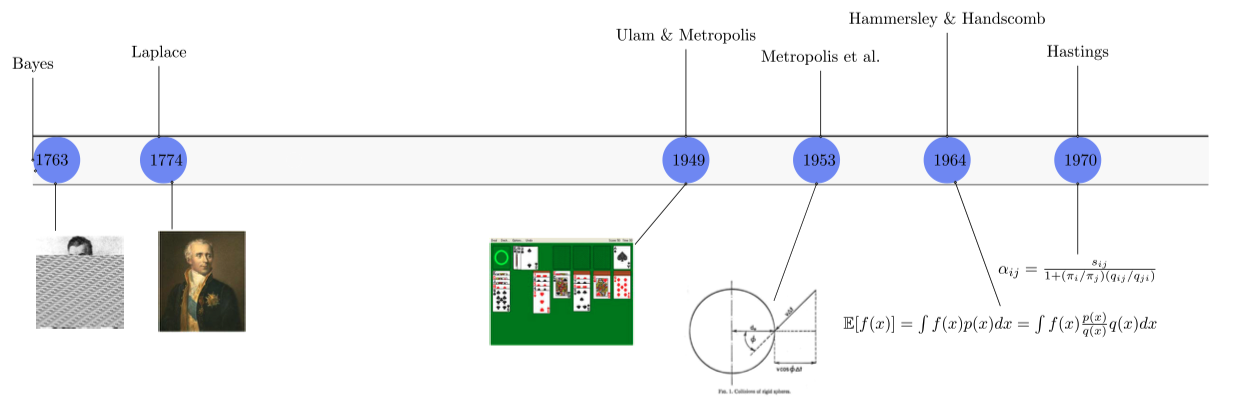
Metropolis+ (1953) Equation of State Calculations by Fast Computing Machines
Metropolis et. al. [The Journal of Chemical Physics 21(1953) 1087-1092] は初の MCMC(乱歩 Metropolis 法)を,対称分布を Gibbs の正準分布として,“modified Monte Carlo scheme” という名前の下で提案し,剛円板モデルのシミュレーションに応用した論文である.重点サンプリングを “Monte Carlo method” と呼び,「目標分布から直接サンプルを生成できるために提案分布と目標分布とのズレによる性能劣化がない」ことを美点として挙げている.この手法は後の (Hastings, 1970) による改良と併せて,Metropolis-Hastings 法と呼ばれるようになる.
Duane+ (1987) Hybrid Monte Carlo
Duane et al. [Phys. B 195(1987) 216-222] は Hamiltonian Monte Carlo 法の提案論文と目されているが,その実は全く違う文脈の中で提案された.場の量子論における (Parisi and Wu, 1981) の確率過程量子化や小正準法にように,正確に物理的過程をシミュレーションする必要はないのである.これを Metropolis 法の提案核に使うことを提案した論文である.
Peters and de With (2012) Rejection-Free Monte Carlo Sampling for General Potentials
Peters and de With [Phys. E 85(2012) 026703] は Metropolis 法による棄却-採択の代わりに,衝突により方向を変える粒子を想定することで,効率的な Monte Carlo 法を実行することを目指した.ただの event-driven な molecular dynamics と違い,一般の滑らかなポテンシャルに適用可能である点が革新的である.しかし,粒子系のポテンシャルは常に和の形で表されるように,一般の PDMP に基づいた連続時間 MCMC 手法も,適用可能なモデルの範囲が限定されている点が難点である (Nemeth and Fearnhead, 2021).
Dai+ (2019) Monte Carlo Fusion
(Dai et al., 2019) は有限混合で表される分布からのサンプリング法(Fusion 問題)に関する最初の理論解析である.
Fearnhead+ (2017) Continuous-time Importance Sampling: Monte Carlo Methods which Avoid Time-Discretization Error
(Fearnhead et al., 2017) は拡散過程を離散化誤差なしにシミュレーションする手法を提案している.逐次重点サンプリング(SIS)の連続時間極限を考えることで,提案過程と重点荷重との組がPDMPとなり,効率的なシミュレーションが可能になる.
最適輸送とそのエントロピー緩和
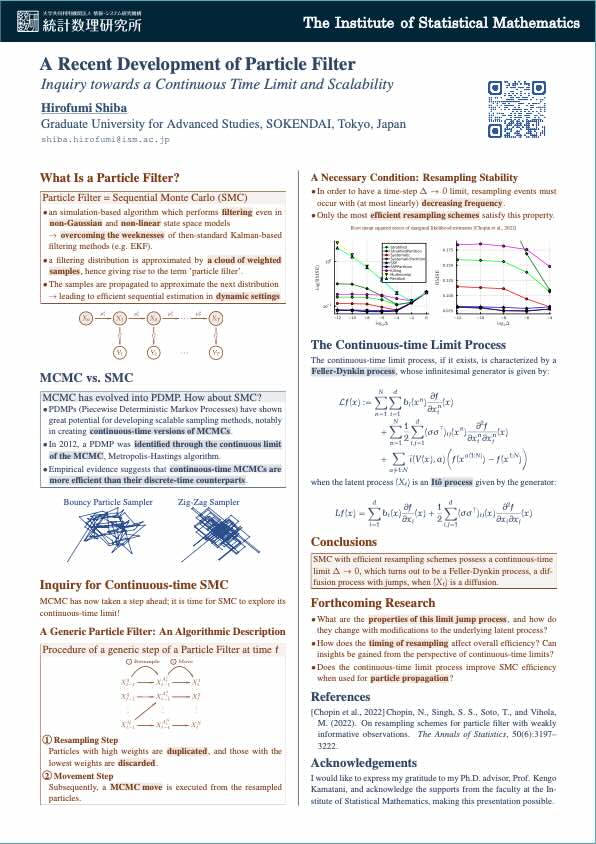
A Recent Development of Particle Methods
変分推論1
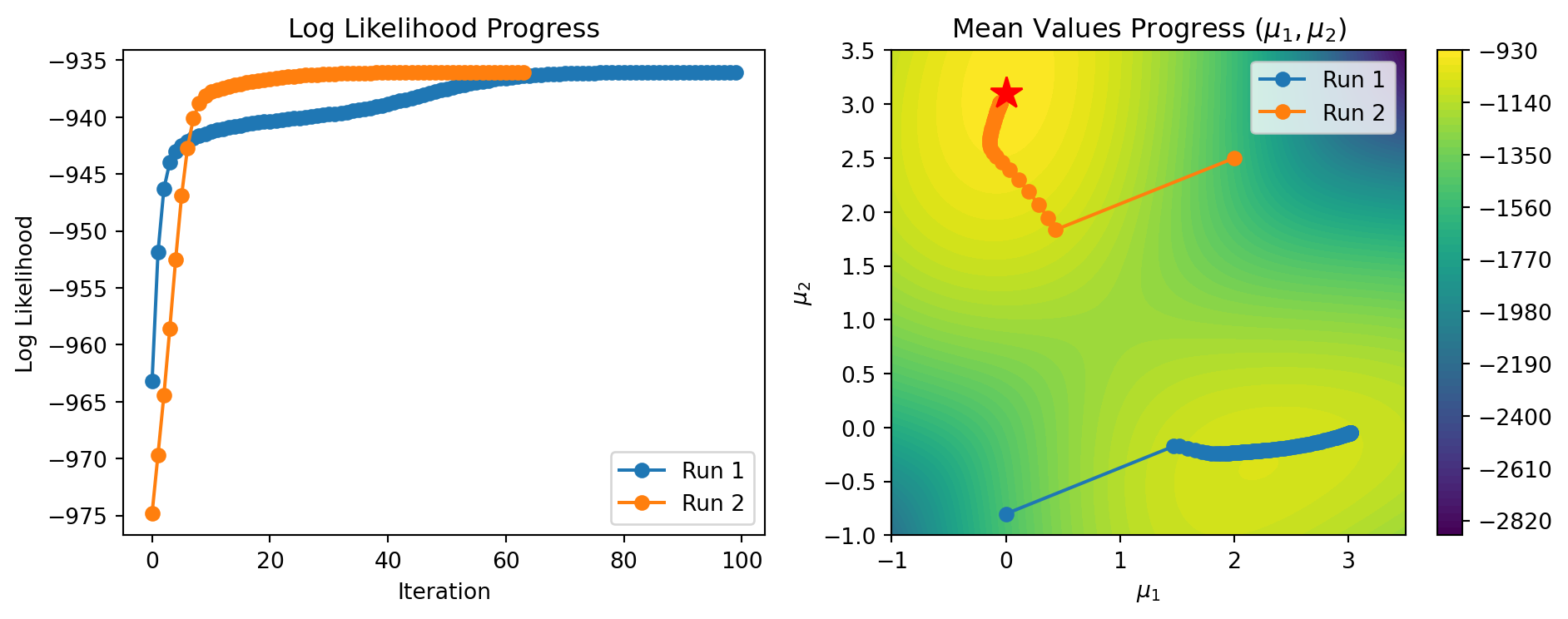
本稿では,\(K\)-平均アルゴリズム によるクラスタリングの考え方と問題点を,Python による実演を通じてみる.次稿 で,\(K\)-平均アルゴリズムの model-aware な一般化として EM アルゴリズム を説明し,その共通の問題点「初期値依存性」と「局所解へのトラップ」の数理的な理解を目指す.






















.svg)